Détection de collision et théorème de l'axe de division

De nos jours, les ordinateurs sont des ordinateurs puissants

capables d'effectuer des millions d'opérations par seconde. Et naturellement, vous ne pouvez pas vous passer de la simulation du monde réel ou du jeu. L'un des problèmes de la modélisation et de la simulation par ordinateur est de déterminer la collision de deux objets, dont l'une des solutions est réalisée par le théorème sur l'axe de séparation.







Remarque. L'article donnera un exemple avec 2 parallélépipèdes (ci-après - cubes), mais l'idée d'autres objets convexes sera préservée.

Remarque. Toutes les implémentations seront effectuées dans Unity.

Acte 0. Théorie générale

Tout d'abord, vous devez vous familiariser avec le " théorème d'hyperplan de séparation ", qui servira de base à l'algorithme.



Théorème. Deux géométries convexes ne se croisent pas si et seulement s'il existe un hyperplan entre elles qui les sépare. L'axe orthogonal à l'

hyperplan de division est appelé axe de division et les projections des figures sur celui-ci ne se croisent pas.





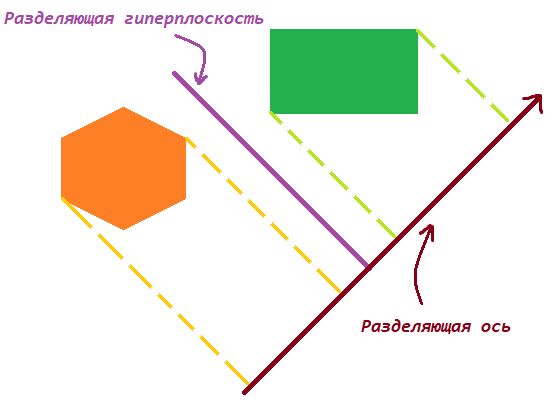
Axe de division (cas 2D)





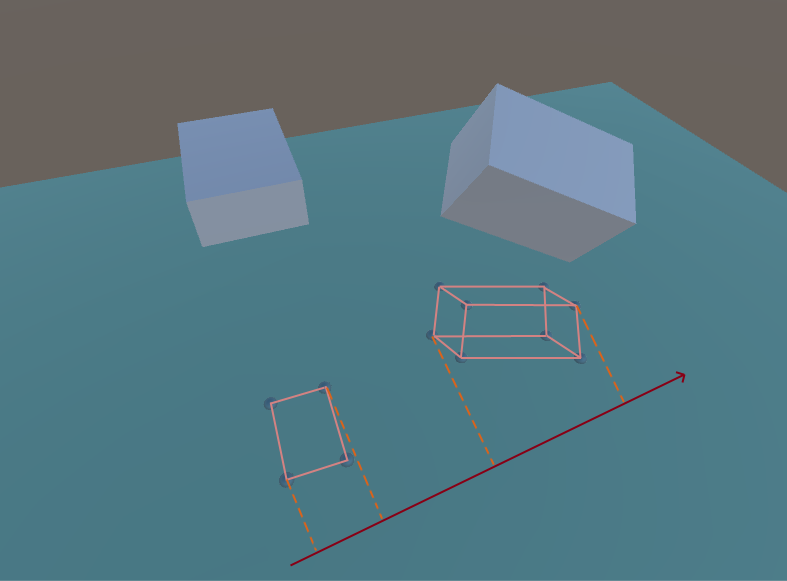
Axe de division (cas 3D)

Vous remarquerez peut-être que les projections sur l'axe de division ne se croisent pas.



Propriété. L'axe de division potentiel sera dans les ensembles suivants:

• Normes planes de chaque cube (rouge)
• Produit vectoriel des bords des cubes $$$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$,

   où X est les bords du premier cube (vert) et Y est le second (bleu).







Nous pouvons décrire chaque cube avec les données d'entrée suivantes:

• Coordonnées du centre du cube
• Dimensions du cube (hauteur, largeur, profondeur)
• Quaternion du cube

Créons pour cela une classe supplémentaire, dont les instances fourniront des informations sur le cube.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

Acte 1. Quaternions

Comme c'est souvent le cas, un objet peut tourner dans l'espace. Afin de trouver les coordonnées des sommets, en tenant compte de la rotation du cube, vous devez comprendre ce qu'est un quaternion.



Quaternion est un nombre hypercomplexe qui détermine la rotation d'un objet dans l'espace.

$$

$$w+xi+yj+zk$$

La partie imaginaire (x, y, z) représente un vecteur qui définit le sens de rotation. La

partie réelle (w) définit l'angle auquel la rotation sera effectuée.



Sa principale différence par rapport à tous les angles d'Euler habituels est qu'il nous suffit d'avoir un vecteur, qui déterminera le sens de rotation, que trois vecteurs linéairement indépendants qui font pivoter l'objet dans 3 sous-espaces.



Je recommande deux articles qui vont plus en détail sur les quaternions:



Un

Deux



Maintenant que nous avons une compréhension minimale des quaternions, comprenons comment faire pivoter un vecteur et décrire la fonction de rotation d'un vecteur avec un quaternion.



Formule de rotation vectorielle

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$$\vec{v}'$ Est le vecteur requis

$$$\vec{v}$ - vecteur original

$$$q$ - quaternion

$$$\overline{q}$- quaternion inverse



Pour commencer, donnons le concept de quaternion inverse sur une base orthonormée - c'est un quaternion avec une partie imaginaire du signe opposé.



$$$q = w+xi+yj+zk$

$$$\overline{q} = w-xi-yj-zk$



Comptons $$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



Maintenant, nous allons écrire les composants individuels et à partir de ce produit, nous allons collecter un nouveau quaternion

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



Comptons le reste, c'est-à-dire $$$q*M$et obtenez le vecteur souhaité.



Remarque. Afin de ne pas surcharger les calculs, nous ne présentons que la partie imaginaire (vectorielle) de ce produit. Après tout, c'est elle qui caractérise le vecteur souhaité.



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



Collectons les composants du vecteur



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

Ainsi, le vecteur requis est obtenu, écrivez le



code:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

Acte 2. Trouver les sommets d'un cube

Sachant comment faire pivoter un vecteur avec un quaternion, il ne sera pas difficile de trouver tous les sommets du cube.



Passons à la fonction de recherche des sommets d'un cube. Définissons les variables de base.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

Ensuite, vous devez trouver un point (point d'ancrage) à partir duquel il sera plus facile de trouver d'autres sommets.



Soustrayez la moitié de la dimension du cube de la coordonnée centrale, puis ajoutez une dimension de cube au point de pivot.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

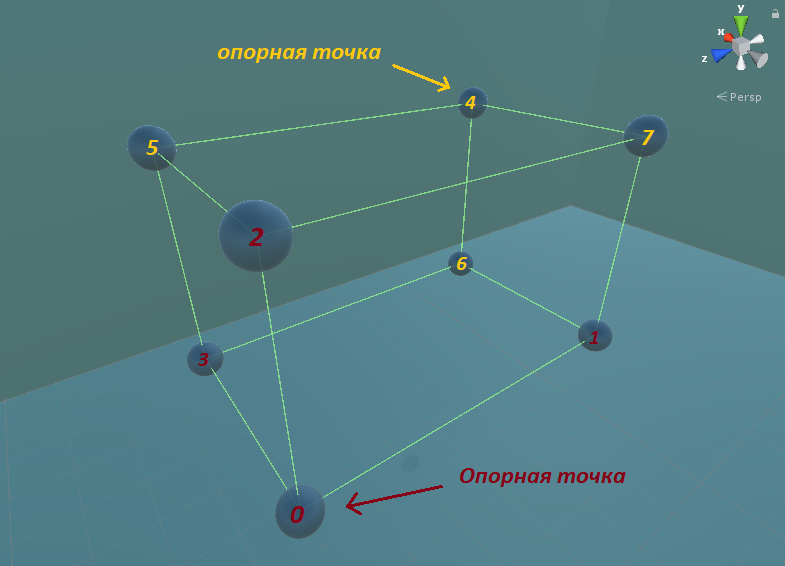
Nous pouvons voir comment les points sont formés.Après



avoir trouvé les coordonnées des sommets, vous devez faire pivoter chaque vecteur du quaternion correspondant.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

Passons aux projections.

Acte 3. Recherche d'axes de division

L'étape suivante consiste à trouver l'ensemble des axes qui prétendent se diviser.

Rappelez-vous qu'il peut être trouvé dans les ensembles suivants:

• Normales planes de chaque cube (rouge)
• Produit vectoriel des bords des cubes $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$où X est les bords du premier cube (vert) et Y est le second (bleu).

Pour obtenir les axes nécessaires, il suffit d'avoir quatre sommets du cube, qui forment un système orthogonal de vecteurs. Ces sommets se trouvent dans les quatre premières cellules du tableau de points que nous avons formé dans le deuxième acte.







Il faut trouver les normales planes générées par les vecteurs:

• $$$\vec{a}$ et $$$\vec{b}$
• $$$\vec{b}$ et $$$\vec{c}$
• $$$\vec{a}$ et $$$\vec{c}$

Pour ce faire, il est nécessaire d'itérer sur les paires d'arêtes du cube pour que chaque nouvel échantillon forme un plan orthogonal à tous les plans obtenus précédemment. Il a été extrêmement difficile pour moi d'expliquer comment cela fonctionne, j'ai donc fourni deux versions du code pour vous aider à comprendre.





Mais vous pouvez faciliter les choses:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

Nous devons également trouver tous les produits vectoriels des bords des cubes. Cela peut être organisé par une simple recherche:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

Acte 4. Projections sur l'axe

Nous sommes arrivés au point le plus important. Ici, nous devons trouver les projections des cubes sur tous les axes de division potentiels. Le théorème a une conséquence importante: si les objets se croisent, alors l'axe sur lequel l'intersection de la projection des cubes est minimale est la direction (normale) de la collision, et la longueur du segment d'intersection est la profondeur de pénétration.



Mais d'abord, rappelons la formule pour la projection scalaire du vecteur v sur le vecteur unitaire a :

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

Nous allons maintenant décrire une fonction qui déterminera l'intersection des projections sur les axes candidats.



L'entrée est les sommets de deux cubes et une liste d'axes de division potentiels:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

La projection sur l'axe est définie par deux points qui ont des valeurs maximum et minimum sur l'axe lui-même:







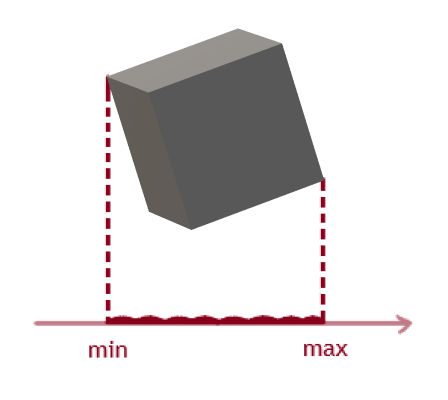
Ensuite, nous créons une fonction qui renvoie les points de projection de chaque cube. Il prend deux paramètres de retour, un tableau de sommets et un axe de division potentiel.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

Donc, en appliquant cette fonction ( ProjAxis ), nous obtenons les points de projection de chaque cube.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

Ensuite, en fonction des sommets de projection, nous déterminons l'intersection des projections:







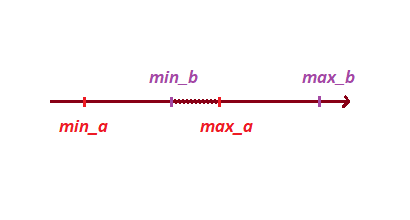
pour ce faire, mettons nos points dans un tableau et trions-le, cette méthode nous aidera à déterminer non seulement l'intersection, mais aussi la profondeur de l'intersection.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

Notez la propriété suivante:



1) Si les segments ne se croisent pas , alors la somme des segments sera inférieure au segment par les points extrêmes formés:







2) Si les segments se croisent , alors la somme des segments sera supérieure au segment par les points extrêmes formés:







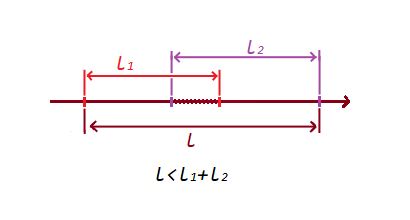
Avec une condition aussi simple, nous avons vérifié l' intersection et la non-intersection segments.



S'il n'y a pas d'intersection, alors la profondeur de l'intersection sera nulle:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

Ainsi, il nous suffit d'avoir au moins un vecteur sur lequel les projections des cubes ne se croisent pas, alors les cubes eux-mêmes ne se croisent pas. Par conséquent, lorsque nous trouvons l'axe de division, nous pouvons ignorer la vérification des vecteurs restants et terminer l'algorithme.



Dans le cas d'intersection de cubes, tout est un peu plus intéressant: la projection des cubes sur tous les vecteurs se croisera, et il faut définir le vecteur avec l'intersection minimum.



Créons ce vecteur avant la boucle, et nous stockerons le vecteur avec la longueur minimale. Ainsi, en fin de cycle, on obtient le vecteur souhaité.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

Et chaque fois que nous trouvons l'axe sur lequel les projections se croisent, nous vérifions s'il est le plus petit de tous. nous multiplions un tel axe par la longueur de l'intersection, et le résultat sera la normale (direction) d'intersection des cubes souhaitée.



J'ai également ajouté une définition de l'orientation de la normale par rapport au premier cube.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

Conclusion

Le projet avec l'implémentation et l'exemple est téléchargé sur GitHub, et vous pouvez le voir ici .



Mon objectif était de partager mon expérience dans la résolution de problèmes liés à la détermination des intersections de deux objets convexes. Et il est également accessible et compréhensible de parler de ce théorème.