où q est la charge de la particule, r ij est la distance entre les particules, C est une certaine constante selon le choix des unités de mesure. En SI c'est - , dans SGS - 1, dans mon programme (où l'énergie est exprimée en électron-volts, la distance en angströms et la charge en charges élémentaires) C est approximativement égal à 14,3996.
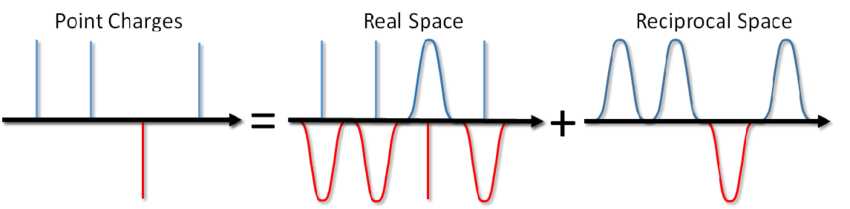
Alors quoi, dites-vous? Ajoutez simplement le terme correspondant au potentiel de la paire et vous avez terminé. Cependant, le plus souvent dans la modélisation MD, des conditions aux limites périodiques sont utilisées, c.-à-d. le système simulé est entouré de tous côtés par un nombre infini de ses copies virtuelles. Dans ce cas, chaque image virtuelle de notre système interagira avec toutes les particules chargées à l'intérieur du système selon la loi de Coulomb. Et puisque l'interaction de Coulomb diminue très faiblement avec la distance (comme 1 / r), alors il n'est pas si facile de la rejeter, en disant qu'on ne peut pas la calculer à partir de telle ou telle distance. Une série de la forme 1 / x diverge, i.e. son montant, en principe, peut croître indéfiniment. Et maintenant, tu ne sales pas un bol de soupe? Cela vous tuera-t-il avec l'électricité?
... vous pouvez non seulement saler la soupe, mais aussi calculer l'énergie de l'interaction coulombienne dans des conditions aux limites périodiques. Cette méthode a été proposée par Ewald en 1921 pour calculer l'énergie d'un cristal ionique (vous pouvez également la voir sur Wikipedia ). L'essence de la méthode consiste à filtrer les charges ponctuelles, puis à soustraire la fonction de filtrage. Dans ce cas, une partie de l'interaction électrostatique est réduite à une action de courte durée et elle peut être simplement coupée de manière standard. La partie longue portée restante est effectivement additionnée dans l'espace de Fourier. En omettant la conclusion, qui peut être consultée dans l'article de Blinov ou dans le même livre de Frenkel et Smith , j'écrirai immédiatement une solution appelée la somme d'Ewald:
où α est un paramètre qui régule le rapport des calculs dans les espaces avant et arrière, k sont des vecteurs dans l'espace réciproque sur lequel la sommation a lieu, V est le volume du système (dans l'espace avant). La première partie (E real ) est à courte portée et est calculée dans le même cycle que les autres potentiels de paire, voir la fonction real_ewald dans l'article précédent. La dernière contribution (E onst ) est une correction pour l'auto-interaction et est souvent appelée la "partie constante" car elle ne dépend pas des coordonnées des particules. Son calcul est trivial, nous nous concentrerons donc uniquement sur la deuxième partie de la somme d'Ewald (E rec), sommation dans l'espace réciproque. Naturellement, au moment de la dérivation d'Ewald, il n'y avait pas de dynamique moléculaire; je n'ai pas pu trouver qui a utilisé cette méthode en premier dans MD. De nos jours, tout livre sur MD contient sa présentation comme une sorte d'étalon-or. Pour réserver, Allen a même fourni un exemple de code dans Fortran. Heureusement, j'ai toujours le code qui était autrefois écrit en C pour la version séquentielle, j'ai juste besoin de le paralléliser (je me suis permis d'omettre certaines déclarations de variables et d'autres détails insignifiants):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
Quelques explications pour le code: la fonction calcule l' exposant complexe (dans les commentaires du code, il est noté iexp pour supprimer l'unité imaginaire des crochets) à partir du produit vectoriel du vecteur k et du vecteur rayon de la particule pour tous les k-vecteurs et pour toutes les particules. Cet exposant est multiplié par la charge des particules. Ensuite, la somme de ces produits pour toutes les particules est calculée (la somme interne dans la formule de E rec ), en Frenkel, elle est appelée la densité de charge et en Blinov, elle est appelée le facteur structurel. Et puis, sur la base de ces facteurs structurels, l'énergie et les forces agissant sur les particules sont calculées. Les composantes des k-vecteurs (2π * l / a, 2π * m / b, 2π * n / c) sont caractérisées par trois entiers l , m et n, qui s'exécutent par cycles jusqu'aux limites spécifiées par l'utilisateur. Les paramètres a, b et c sont les dimensions du système simulé dans les dimensions x, y et z, respectivement (la conclusion est correcte pour un système avec une géométrie parallélépipédique rectangulaire). Dans le code, 1 / a , 1 / b et 1 / c correspondent aux variables ra , rb et rc . Les tableaux pour chaque valeur sont présentés en deux exemplaires: pour les parties réelle et imaginaire. Chaque k-vecteur suivant dans une dimension est obtenu de manière itérative à partir du précédent en multipliant par un complexe le précédent, afin de ne pas compter le sinus avec cosinus à chaque fois. Les tableaux emc / s et enc / s sont remplis pour tous les met n , respectivement, et le tableau elc / s place la valeur de chaque l > 1 dans l'indice nul de l afin d'économiser de la mémoire.
A des fins de parallélisation, il est avantageux d '"inverser" l'ordre des cycles de sorte que le cycle extérieur passe sur les particules. Et ici, nous voyons un problème - cette fonction ne peut être parallélisée qu'avant de calculer la somme sur toutes les particules (densité de charge). D'autres calculs sont basés sur ce montant, et il ne sera calculé que lorsque tous les threads auront terminé leur travail, vous devez donc diviser cette fonction en deux. Le premier calcule la densité de charge et le second calcule l'énergie et les forces. Notez que la deuxième fonction nécessitera à nouveau la quantité q iiexp (kr) pour chaque particule et pour chaque k-vecteur, calculé à l'étape précédente. Et ici, il y a deux approches: soit recalculer à nouveau, soit s'en souvenir.
La première option prend plus de temps, la seconde - plus de mémoire (nombre de particules * nombre de k-vecteurs * sizeof (float2)). J'ai opté pour la deuxième option:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
J'espère que vous me pardonnerez de laisser des commentaires en anglais, le code est pratiquement le même que la version série. Le code est même devenu plus lisible en raison du fait que les tableaux ont perdu une dimension: elc / s [i] [l] , emc / s [i] [m] et enc / s [i] [n] transformé en el unidimensionnel , em et fr , tableaux lmc / s et ckc / s - dans les variables lm et ck (la dimension par particules a disparu, puisqu'il n'est plus nécessaire de la stocker pour chaque particule, le résultat intermédiaire est accumulé en mémoire partagée). Malheureusement, un problème s'est immédiatement posé: les tableaux em et endevait être défini statique pour ne pas utiliser la mémoire globale et ne pas allouer dynamiquement de la mémoire à chaque fois. Le nombre d'éléments qu'ils contiennent est déterminé par la directive NKVEC_MX (le nombre maximum de k-vecteurs dans une dimension) au stade de la compilation, et seuls les premiers éléments nky / z sont utilisés à l'exécution. De plus, un index de bout en bout pour tous les k-vecteurs et une directive similaire sont apparus, limitant le nombre total de ces vecteurs NTOTKVEC . Le problème se posera si l'utilisateur a besoin de plus de k-vecteurs que spécifié par les directives. Pour calculer l'énergie, un bloc d'indice nul est fourni, car peu importe quel bloc effectuera ce calcul et dans quel ordre. Notez que la valeur calculée dans la variable akkle code série ne dépend que de la taille du système simulé et peut être calculé au stade de l'initialisation, dans mon implémentation, il est stocké dans le tableau md-> exprk2 [] pour chaque k-vecteur. De même, les composantes des k-vecteurs sont tirées du tableau md-> rk [] . Ici, il pourrait être nécessaire d'utiliser des fonctions FFT prêtes à l'emploi, car la méthode est basée sur elle, mais je n'ai toujours pas compris comment le faire.
Eh bien, essayons maintenant de compter quelque chose, mais le même chlorure de sodium. Prenons 2 mille ions sodium et la même quantité de chlore. Définissons les charges comme des entiers, et prenons les potentiels de paire, par exemple, de ce travail. Définissons la configuration de départ au hasard et mélangeons-la légèrement, figure 2a. On choisit le volume du système pour qu'il corresponde à la densité du chlorure de sodium à température ambiante (2,165 g / cm 3 ). Commençons tout cela pendant une courte période (10'000 pas de 5 femtosecondes) avec une considération naïve de l'électrostatique selon la loi de Coulomb et en utilisant la sommation d'Ewald. Les configurations résultantes sont représentées sur les figures 2b et 2c, respectivement. Il semble que dans le cas d'Ewald, le système soit un peu plus rationalisé que sans lui. Il est également important que les fluctuations d'énergie totales aient considérablement diminué avec l'utilisation de la sommation.

Figure 2. Configuration initiale du système NaCl (a) et après 10'000 étapes d'intégration: méthode naïve (b) et avec le schéma d'Ewald (c).
Au lieu d'une conclusion
Notez que la structure obtenue sur la figure ne correspond pas au réseau cristallin NaCl, mais plutôt au réseau ZnS, mais c'est déjà une plainte concernant les potentiels de paire. La prise en compte de l'électrostatique est très importante pour la modélisation de la dynamique moléculaire. On pense que c'est l'interaction électrostatique qui est responsable de la formation des réseaux cristallins, car elle agit à de grandes distances. Certes, à partir de cette position, il est difficile d'expliquer comment des substances telles que l'argon cristallisent pendant le refroidissement.
En plus de la méthode Ewald mentionnée, il existe également d'autres méthodes de comptabilisation de l'électrostatique, voir, par exemple, cette revue .