
Source: unsplash.com
Selon Jackie Stewart, triple champion du monde de Formule 1, comprendre la voiture l'a aidé à devenir un meilleur pilote: "Un coureur n'a pas besoin d'être un ingénieur, mais un intérêt pour la mécanique ."
Martin Thompson (créateur de LMAX Disruptor ) a appliqué ce concept à la programmation. En un mot, comprendre le matériel sous-jacent améliorera vos compétences en matière de conception d'algorithmes, de structures de données, etc.
L'équipe Mail.ru Cloud Solutions a traduit un article qui a approfondi la conception du processeur et a examiné comment la compréhension de certains des concepts de processeur peut vous aider à prendre de meilleures décisions.
Les bases
Les processeurs modernes sont basés sur le concept de multitraitement symétrique (SMP). Un processeur est conçu de telle sorte que deux cœurs ou plus partagent une mémoire commune (également appelée mémoire principale ou mémoire vive).
De plus, pour accélérer l'accès à la mémoire, le processeur dispose de plusieurs niveaux de cache: L1, L2 et L3. L'architecture exacte dépend du fabricant, du modèle de processeur et d'autres facteurs. Le plus souvent, cependant, les caches L1 et L2 fonctionnent localement pour chaque cœur, tandis que L3 est partagé entre tous les cœurs.

Architecture SMP
Plus le cache est proche du cœur du processeur, plus la latence d'accès et la taille du cache sont faibles:
| Cache | Retard | Cycles CPU | La taille |
| L1 | ~ 1,2 ns | ~ 4 | Entre 32 et 512 Ko |
| L2 | ~ 3 ns | ~ 10 | Entre 128 Ko et 24 Mo |
| L3 | ~ 12 ns | ~ 40 | Entre 2 et 32 Mo |
Encore une fois, les nombres exacts dépendent du modèle de processeur. Pour une estimation approximative, si l'accès à la mémoire principale prend 60 ns, l'accès à L1 est environ 50 fois plus rapide.
Dans le monde des processeurs, il existe un concept important de localité de liaison . Lorsque le processeur accède à un emplacement mémoire spécifique, il est très probable que:
- Il se référera au même emplacement mémoire dans un proche avenir - c'est le principe de la localité temporelle .
- Il se référera aux cellules mémoire situées à proximité - c'est le principe de la localité par distance .
La localité temporelle est l'une des raisons des caches CPU. Mais comment utilisez-vous la localité à distance? Solution - au lieu de copier une cellule de mémoire dans les caches du processeur, la ligne de cache y est copiée. Une ligne de cache est un segment contigu de mémoire.
La taille de la ligne de cache dépend du niveau de cache (et encore une fois du modèle de processeur). Par exemple, voici la taille de la ligne de cache L1 sur ma machine:
$ sysctl -a | grep cacheline
hw.cachelinesize: 64
Au lieu de copier une seule variable dans le cache L1, le processeur y copie un segment contigu de 64 octets. Par exemple, au lieu de copier un seul élément int64 d'une tranche Go, il copie cet élément plus sept autres éléments int64.
Utilisations spécifiques des lignes de cache dans Go
Regardons un exemple concret qui démontre les avantages des caches de processeur. Dans le code suivant, nous ajoutons deux matrices carrées d'éléments int64:
func BenchmarkMatrixCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
}
}
}
}
S'il est
matrixLengthégal à 64k, il produit le résultat suivant:
BenchmarkMatrixSimpleCombination-64000 8 130724158 ns/op
Maintenant, à la place,
matrixB[i][j]nous ajouterons matrixB[j][i]:
func BenchmarkMatrixReversedCombination(b *testing.B) {
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i++ {
for j := 0; j < matrixLength; j++ {
matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
}
}
}
}
Cela affectera-t-il les résultats?
BenchmarkMatrixCombination-64000 8 130724158 ns/op
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
Oui, c'est vrai, et assez radicalement! Comment cela peut-il être expliqué?
Essayons de dessiner ce qui se passe. Le cercle bleu indique la première matrice et le cercle rose indique la seconde. Lorsque nous définissons
matrixA[i][j] = matrixA[i][j] + matrixB[j][i], le pointeur bleu est à la position (4.0) et le rose est à la position (0.4):
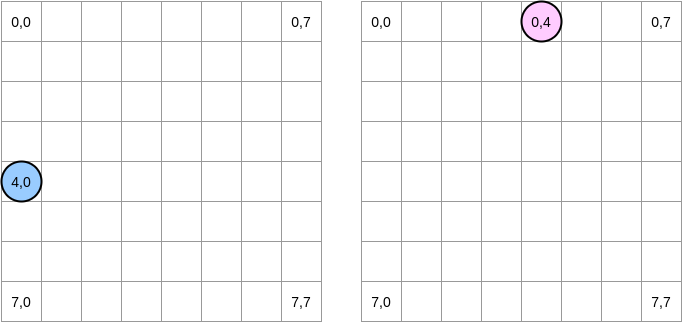
Remarque . Dans ce diagramme, les matrices sont présentées sous forme mathématique: avec une abscisse et une ordonnée, et la position (0,0) est dans le carré supérieur gauche. En mémoire, toutes les lignes de la matrice sont disposées séquentiellement. Cependant, par souci de clarté, regardons la représentation mathématique. De plus, dans les exemples suivants, la taille de la matrice est un multiple de la taille de la ligne de cache. Par conséquent, la ligne de cache ne «rattrapera» pas la ligne suivante. Cela semble compliqué, mais les exemples clarifieront tout.
Comment allons-nous itérer sur les matrices? Le pointeur bleu se déplace vers la droite jusqu'à ce qu'il atteigne la dernière colonne, puis passe à la ligne suivante à la position (5,0), et ainsi de suite. Inversement, le pointeur rose se déplace vers le bas puis passe à la colonne suivante.
Lorsque le pointeur rose atteint la position (0.4), le processeur met en cache la ligne entière (dans notre exemple, la taille de la ligne de cache est de quatre éléments). Ainsi, lorsque le pointeur rose atteint la position (0,5), nous pouvons supposer que la variable est déjà présente dans L1, non?
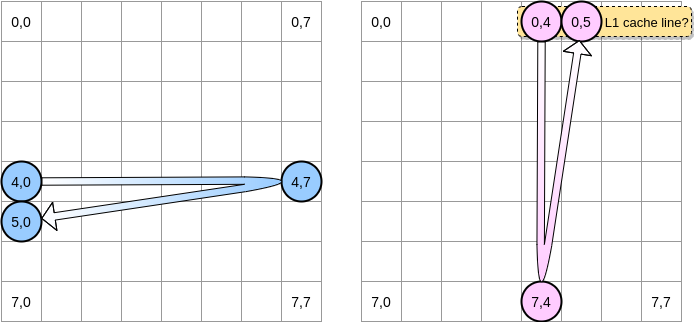
La réponse dépend de la taille de la matrice :
- Si la matrice est suffisamment petite par rapport à la taille de L1, alors oui, l'élément (0.5) sera déjà mis en cache.
- Sinon, la ligne de cache sera supprimée de L1 avant que le pointeur n'atteigne la position (0,5). Par conséquent, il générera un échec de cache et le processeur devra accéder à la variable d'une manière différente, par exemple via L2. Nous serons dans cet état:
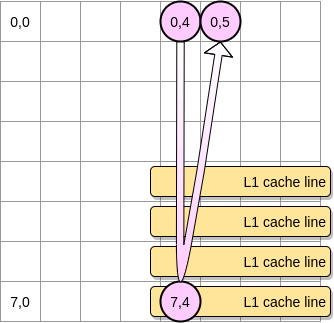
Quelle doit être la taille d'une matrice pour bénéficier de L1? Comptons un peu. Tout d'abord, vous devez connaître la taille du cache L1:
$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768
Sur ma machine, le cache L1 est de 32 768 octets tandis que la ligne de cache L1 est de 64 octets. De cette façon, je peux stocker jusqu'à 512 lignes de cache en L1. Et si nous exécutions le même benchmark avec une matrice de 512 éléments?
BenchmarkMatrixCombination-512 1404 718594 ns/op
BenchmarkMatrixReversedCombination-512 1363 850141 ns/opp
Bien que nous ayons corrigé l'écart (sur une matrice 64k, la différence était d'environ 4 fois), nous pouvons quand même remarquer une légère différence. Qu'est-ce qui ne va pas? Dans les benchmarks, nous travaillons avec deux matrices. Par conséquent, le processeur doit conserver les lignes de cache des deux. Dans un monde idéal (aucune autre application en cours d'exécution et ainsi de suite), le cache L1 est rempli à 50% des données de la première matrice et à 50% de la seconde. Et si nous réduisions la taille de la matrice de moitié pour travailler avec 256 éléments:
BenchmarkMatrixCombination-256 5712 176415 ns/op
BenchmarkMatrixReversedCombination-256 6470 164720 ns/op
Enfin, nous avons atteint le point où les deux résultats sont (presque) équivalents.
. ? , Go. - LEA (Load Effective Address). , . LEA .
, int64 , LEA , 8 . , . , . , () .
Maintenant - comment limiter l'impact des échecs de cache dans le cas d'une matrice plus grande? Il existe une méthode, qui s'appelle l' optimisation des boucles imbriquées ( optimisation de l'imbrication de boucles ). Pour tirer le meilleur parti des lignes de cache, nous ne devons itérer que dans un bloc donné.
Définissons un bloc dans notre exemple comme un carré de 4 éléments. Dans la première matrice, on itère de (4.0) à (4.3). Passez ensuite à la ligne suivante. En conséquence, nous itérons sur la deuxième matrice uniquement de (0,4) à (3,4) avant de passer à la colonne suivante.
Lorsque le pointeur rose passe sur la première colonne, le processeur stocke la ligne de cache correspondante. Ainsi, parcourir le reste du bloc signifie profiter de L1:
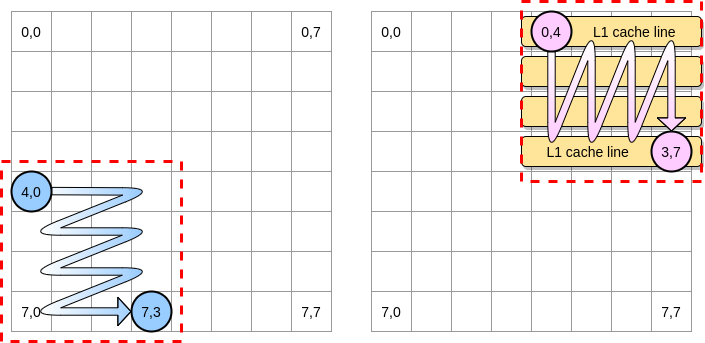
Écrivons une implémentation de cet algorithme dans Go, mais nous devons d'abord choisir soigneusement la taille du bloc. Dans l'exemple précédent, il était égal à la ligne de cache. Il ne doit pas être plus petit, sinon nous stockerons des éléments qui ne seront pas accessibles.
Dans notre benchmark Go, nous stockons des éléments int64 (8 octets chacun). La ligne de cache est de 64 octets, elle peut donc contenir 8 éléments. Ensuite, la valeur de la taille du bloc doit être d'au moins 8:
func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
matrixA := createMatrix(matrixLength)
matrixB := createMatrix(matrixLength)
blockSize := 8
for n := 0; n < b.N; n++ {
for i := 0; i < matrixLength; i += blockSize {
for j := 0; j < matrixLength; j += blockSize {
for ii := i; ii < i+blockSize; ii++ {
for jj := j; jj < j+blockSize; jj++ {
matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
}
}
}
}
}
}
Notre implémentation est maintenant 67% plus rapide que lorsque nous avons itéré sur toute la ligne / colonne:
BenchmarkMatrixReversedCombination-64000 2 573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000 6 185375690 ns/op
Ce fut le premier exemple à démontrer que la compréhension du fonctionnement des caches CPU peut aider à concevoir des algorithmes plus efficaces.
Faux partage
Nous comprenons maintenant comment le processeur gère les caches internes. En résumé:
- Le principe de localité par distance oblige le processeur à prendre non seulement une adresse mémoire, mais une ligne de cache.
- Le cache L1 est local sur un cœur de processeur.
Discutons maintenant d'un exemple avec la cohérence du cache L1. La mémoire principale stocke deux variables
var1et var2. Un thread sur un noyau accède var1, tandis qu'un autre thread sur l'autre noyau accède var2. En supposant que les deux variables sont continues (ou presque continues), nous nous retrouvons dans une situation où elle est var2présente dans les deux caches.
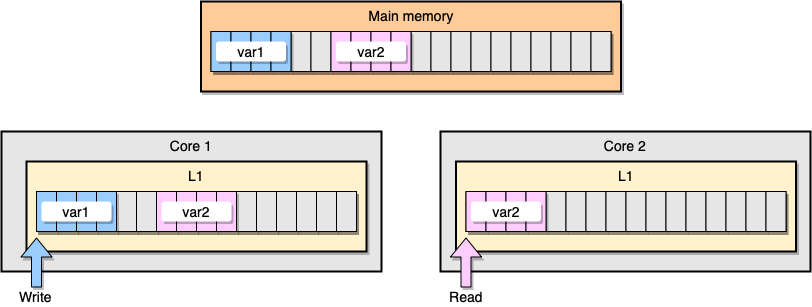
Exemple de cache L1
Que se passe-t-il si le premier thread met à jour sa ligne de cache? Il peut potentiellement mettre à jour n'importe quel emplacement de sa chaîne, y compris
var2. Ensuite, lorsque le deuxième thread lit var2, la valeur peut ne pas être cohérente.
Comment le processeur maintient-il la cohérence du cache? Si deux lignes de cache ont des adresses partagées, le processeur les marque comme partagées. Si un thread modifie une ligne partagée, il marque les deux comme modifiés. La coordination entre les cœurs est nécessaire pour garantir la cohérence des caches, ce qui peut dégrader considérablement les performances des applications. Ce problème s'appelle le faux partage .
Considérons une application Go spécifique. Dans cet exemple, nous créons deux structures l'une après l'autre. Par conséquent, ces structures doivent être séquentielles en mémoire. Ensuite, nous créons deux goroutines, chacune d'entre elles faisant référence à sa propre structure (M est une constante égale à un million):
type SimpleStruct struct {
n int
}
func BenchmarkStructureFalseSharing(b *testing.B) {
structA := SimpleStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Dans cet exemple, la variable n de la deuxième structure n'est disponible que pour la deuxième goroutine. Cependant, comme les structures sont contiguës en mémoire, la variable sera présente dans les deux lignes de cache (en supposant que les deux goroutines sont planifiées sur des threads sur des cœurs séparés, ce qui n'est pas nécessairement le cas). Voici le résultat de référence:
BenchmarkStructureFalseSharing 514 2641990 ns/op
Comment éviter le partage de fausses informations? Une solution est la mémoire complète (remplissage de mémoire). Notre objectif est de nous assurer qu'il y a suffisamment d'espace entre deux variables pour qu'elles appartiennent à des lignes de cache différentes.
Tout d'abord, créons une alternative à la structure précédente en remplissant la mémoire après avoir déclaré la variable:
type PaddedStruct struct {
n int
_ CacheLinePad
}
type CacheLinePad struct {
_ [CacheLinePadSize]byte
}
const CacheLinePadSize = 64
Ensuite, nous instancions les deux structures et continuons d'accéder à ces deux variables dans des goroutines séparées:
func BenchmarkStructurePadding(b *testing.B) {
structA := PaddedStruct{}
structB := SimpleStruct{}
wg := sync.WaitGroup{}
b.ResetTimer()
for i := 0; i < b.N; i++ {
wg.Add(2)
go func() {
for j := 0; j < M; j++ {
structA.n += j
}
wg.Done()
}()
go func() {
for j := 0; j < M; j++ {
structB.n += j
}
wg.Done()
}()
wg.Wait()
}
}
Du point de vue de la mémoire, cet exemple devrait donner l'impression que les deux variables font partie de différentes lignes de cache:
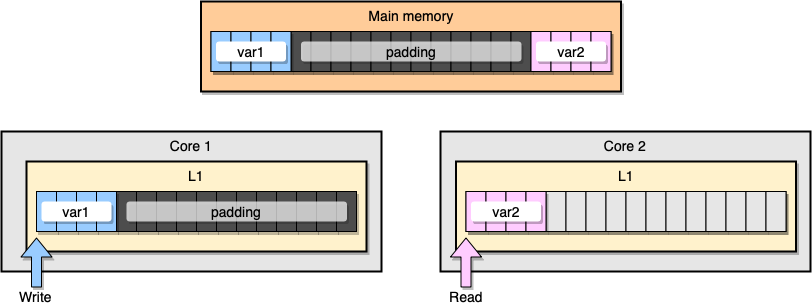
Remplissage de la mémoire
Regardons les résultats:
BenchmarkStructureFalseSharing 514 2641990 ns/op
BenchmarkStructurePadding 735 1622886 ns/op
Un deuxième exemple de remplissage de mémoire est environ 40% plus rapide que notre implémentation d'origine. Mais il y a aussi un inconvénient. La méthode accélère le code, mais nécessite plus de mémoire.
Aimer la mécanique est un concept important lorsqu'il s'agit d'optimiser les applications. Dans cet article, nous avons vu des exemples de la façon dont la compréhension du processeur nous a aidés à améliorer la vitesse du programme.
Quoi d'autre à lire: