
Armored Warfare: Project Armata est un jeu d'action de chars en ligne gratuit développé par Allods Team, le studio de jeux MY.GAMES. Malgré le fait que le jeu soit fait sur CryEngine, un moteur assez populaire avec un bon rendu en temps réel, pour notre jeu, nous devons modifier et créer beaucoup de choses à partir de zéro. Dans cet article, je veux parler de la façon dont nous avons implémenté l'aberration chromatique pour la vue à la première personne, et de quoi il s'agit.
Qu'est-ce que l'aberration chromatique?
L'aberration chromatique est un défaut de la lentille dans lequel toutes les couleurs n'arrivent pas au même point. Cela est dû au fait que l'indice de réfraction du milieu dépend de la longueur d'onde de la lumière (voir dispersion ). Par exemple, voici à quoi ressemble la situation lorsque l'objectif ne souffre pas d'aberration chromatique:
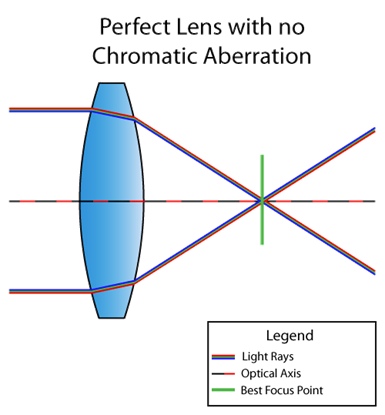
Et voici une lentille avec un défaut:
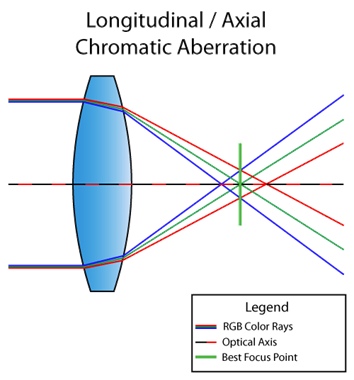
En passant, la situation ci-dessus est appelée aberration chromatique longitudinale (ou axiale). Cela se produit lorsque des longueurs d'onde différentes ne convergent pas au même point dans le plan focal après avoir traversé la lentille. Ensuite, le défaut est visible sur l'image entière:

Dans l'image ci-dessus, vous pouvez voir que les couleurs violettes et vertes se détachent en raison d'un défaut. Ne peux voir? Et sur cette image?

Il existe également une aberration chromatique latérale (ou latérale). Cela se produit lorsque la lumière est incidente à un angle par rapport à l'objectif. En conséquence, différentes longueurs d'onde de la lumière convergent en différents points dans le plan focal. Voici une image à comprendre:
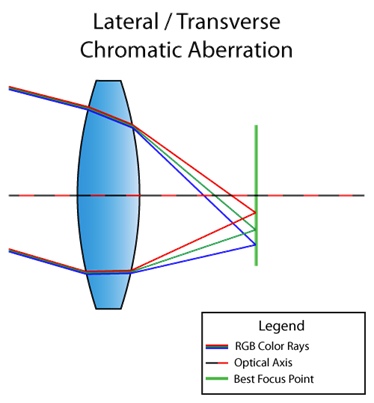
Vous pouvez déjà voir sur le diagramme qu'en conséquence nous obtenons une décomposition complète de la lumière du rouge au violet. Contrairement aux aberrations chromatiques longitudinales, latérales n'apparaissent jamais au centre, mais plus près des bords de l'image. Pour que vous compreniez ce que je veux dire, voici une autre image d'Internet:

Eh bien, puisque nous en avons fini avec la théorie, allons droit au but.
Aberration chromatique latérale avec décomposition de la lumière
Je commencerai par répondre à la question que beaucoup d'entre vous pourraient avoir en tête: "CryEngine n'est-il pas implémenté l'aberration chromatique?" Il y a. Mais il est utilisé au stade du post-traitement dans le même shader avec affûtage, et l'algorithme ressemble à ceci ( lien vers le code ):
screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;Ce qui, en principe, fonctionne. Mais nous avons un jeu sur les chars. Nous n'avons besoin de cet effet que pour la vue à la première personne, et uniquement pour la beauté, c'est-à-dire pour que tout soit net au centre (bonjour à l'aberration latérale) Par conséquent, la mise en œuvre actuelle ne convenait pas au moins au fait que son effet était visible sur toute l'image.
Voici à quoi ressemblait l'aberration elle-même (attention au côté gauche):

Et voici à quoi cela ressemblait si vous tordez les paramètres:

Par conséquent, nous nous sommes fixé comme objectif:
- Mettez en œuvre l'aberration chromatique latérale pour que tout soit net près de la lunette, et si les défauts de couleur caractéristiques ne sont pas visibles sur les côtés, au moins pour être flous.
- Échantillonnez une texture en multipliant les canaux RVB par des coefficients correspondant à une longueur d'onde spécifique. Je n'en ai pas encore parlé, alors il se peut maintenant que ce point ne soit pas tout à fait clair. Mais nous l'examinerons certainement dans tous les détails plus tard.
Examinons d'abord le mécanisme général et le code pour créer une aberration chromatique latérale.
half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;
Ainsi, tout d'abord, un masque circulaire est construit, qui est responsable de la distance du centre de l'écran, puis la direction du centre de l'écran est calculée, puis tout cela est multiplié par
blur. Bluret falloff- ce sont des paramètres qui sont passés de l'extérieur et ne sont que des multiplicateurs pour ajuster l'aberration. De plus, un paramètre est jeté de l'extérieur sampleCount, qui est responsable non seulement du nombre d'échantillons, mais aussi, en fait, du pas entre les points d'échantillonnage, car
half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);
Il ne reste plus qu'à aller
sampleCountune fois à partir d'un point donné de la texture, en décalant à chaque fois de offsetDecrement, multiplier les canaux par les poids d'onde correspondants et diviser par la somme de ces poids. Eh bien, il est temps de parler du deuxième point de notre objectif mondial.
Le spectre visible de la lumière varie de 380 nm (violet) à 780 nm (rouge). Et voilà, la longueur d'onde peut être convertie en palette RVB. En Python, le code qui fait cette magie ressemble à ceci:
def get_color(waveLength):
if waveLength >= 380 and waveLength < 440:
red = -(waveLength - 440.0) / (440.0 - 380.0)
green = 0.0
blue = 1.0
elif waveLength >= 440 and waveLength < 490:
red = 0.0
green = (waveLength - 440.0) / (490.0 - 440.0)
blue = 1.0
elif waveLength >= 490 and waveLength < 510:
red = 0.0
green = 1.0
blue = -(waveLength - 510.0) / (510.0 - 490.0)
elif waveLength >= 510 and waveLength < 580:
red = (waveLength - 510.0) / (580.0 - 510.0)
green = 1.0
blue = 0.0
elif waveLength >= 580 and waveLength < 645:
red = 1.0
green = -(waveLength - 645.0) / (645.0 - 580.0)
blue = 0.0
elif waveLength >= 645 and waveLength < 781:
red = 1.0
green = 0.0
blue = 0.0
else:
red = 0.0
green = 0.0
blue = 0.0
factor = 0.0
if waveLength >= 380 and waveLength < 420:
factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
elif waveLength >= 420 and waveLength < 701:
factor = 1.0
elif waveLength >= 701 and waveLength < 781:
factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
gamma = 0.80
R = (red * factor)**gamma if red > 0 else 0
G = (green * factor)**gamma if green > 0 else 0
B = (blue * factor)**gamma if blue > 0 else 0
return R, G, B
En conséquence, nous obtenons la répartition des couleurs suivante:

En bref, le graphique montre combien et quelle couleur est contenue dans une vague avec une longueur spécifique. Sur l'axe des ordonnées, nous obtenons simplement les mêmes poids que ceux dont j'ai parlé plus tôt. Nous pouvons maintenant implémenter complètement l'algorithme, en tenant compte de ce qui a été dit précédemment:
half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
for (int i = 0; i < sampleCount; i++)
{
waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
Weight.r = GetRedWeight(waveLength);
Weight.g = GetGreenWeight(waveLength);
Weight.b = GetBlueWeight(waveLength);
offset -= offsetDecrement;
color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
accumulator.rgb += color.rgb * Weight.rgb;
WeightSum.rgb += Weight.rgb;
}
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);
Autrement dit, l'idée est que plus nous en avons
sampleCount, moins nous avons de pas entre les points d'échantillonnage, et plus nous dispersons la lumière (nous prenons en compte plus d'ondes de différentes longueurs).
Si ce n'est toujours pas clair, regardons un exemple spécifique, à savoir notre première tentative, et je vais vous expliquer ce qu'il faut prendre
startWaveLengthet endWaveLength, et comment les fonctions seront implémentées GetRed(Green, Blue)Weight.
S'adapte à l'ensemble du spectre visible
Ainsi, à partir du graphique ci-dessus, nous connaissons le rapport approximatif et les valeurs approximatives de la palette RVB pour chaque longueur d'onde. Par exemple, pour une longueur d'onde de 380 nm (violet) (voir le même graphique), on voit que RVB (0,4, 0, 0,4). Ce sont ces valeurs que nous prenons pour les pondérations dont j'ai parlé plus tôt.
Essayons maintenant de nous débarrasser de la fonction d'obtention de couleur par un polynôme du quatrième degré pour que les calculs soient moins chers (nous ne sommes pas un studio Pixar, mais un studio de jeux: moins les calculs sont chers, mieux c'est). Ce polynôme du quatrième degré doit se rapprocher des graphiques résultants. Pour construire le polynôme, j'ai utilisé la bibliothèque SciPy:
wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)
En conséquence, le résultat suivant est obtenu (j'ai divisé en 3 graphiques distincts correspondant à chaque canal séparé, de sorte qu'il est plus facile de comparer avec la valeur exacte):
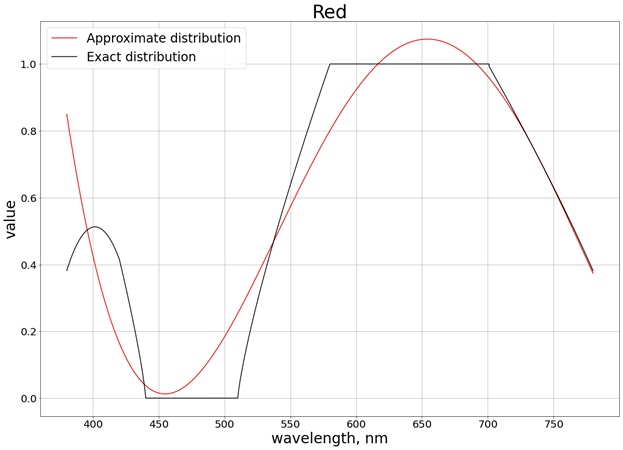
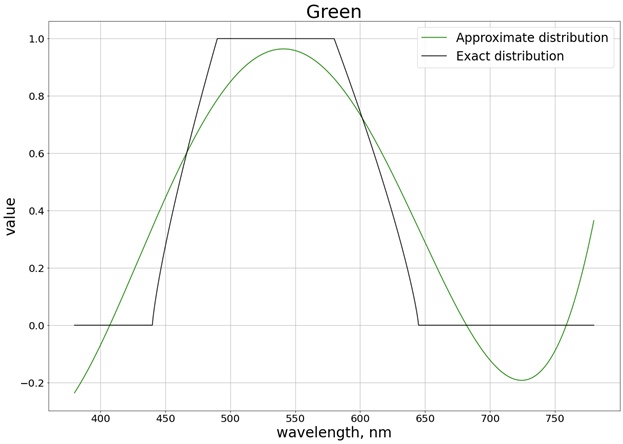
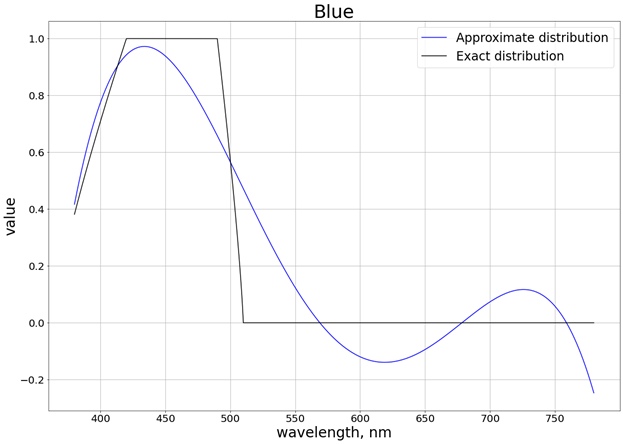
Pour s'assurer que les valeurs ne dépassent pas la limite du segment [0, 1], nous utilisons la fonction
saturate. Pour le rouge, par exemple, la fonction est obtenue:
half GetRedWeight(half x)
{
return saturate(0.8004883122689207 +
1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) -
1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}
Les paramètres manquants
startWaveLengthet endWaveLengthdans ce cas sont respectivement 780 nm et 380 nm. Le résultat en pratique sampleCount=3est le suivant (voir les bords de l'image):

Si nous modifions les valeurs, augmentons
sampleCountà 400, tout devient mieux:

Malheureusement, nous avons un rendu en temps réel dans lequel nous ne pouvons pas autoriser 400 échantillons (environ 3-4) dans un shader. Par conséquent, nous avons légèrement réduit la gamme de longueurs d'onde.
Une partie du spectre visible
Prenons une gamme pour que nous obtenions à la fois des couleurs rouge pur et bleu pur. Nous refusons également la queue rouge à gauche, car elle affecte grandement le polynôme final. En conséquence, nous obtenons la distribution sur le segment [440, 670]:

De plus, il n'est pas nécessaire d'interpoler sur tout le segment, puisque maintenant nous ne pouvons obtenir un polynôme que pour le segment où la valeur change. Par exemple, pour la couleur rouge, il s'agit du segment [510, 580], où la valeur de poids varie de 0 à 1. Dans ce cas, vous pouvez obtenir un polynôme du second ordre, qui est alors
saturateégalement réduit par la fonction à la plage de valeurs [0, 1]. Pour les trois couleurs, nous obtenons le résultat suivant avec prise en compte de la saturation:

En conséquence, nous obtenons, par exemple, le polynôme suivant pour le rouge:
half GetRedWeight(half x)
{
return saturate(0.5764348105166407 +
0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) -
0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}
Et en pratique avec
sampleCount=3:

Dans ce cas, avec les réglages torsadés, on obtient approximativement le même résultat que lors de l'échantillonnage sur toute la gamme du spectre visible:

Ainsi, avec des polynômes du deuxième degré, nous avons obtenu un bon résultat dans la gamme de longueurs d'onde de 440 nm à 670 nm.
Optimisation
En plus d'optimiser les calculs avec des polynômes, vous pouvez optimiser le travail du shader, en vous appuyant sur le mécanisme que nous avons posé dans la base de notre aberration chromatique latérale, à savoir, ne pas effectuer de calculs dans la zone où le déplacement total ne dépasse pas le pixel actuel, sinon nous échantillonnerons le même pixel, et nous l'obtenons.
Cela ressemble à ceci:
bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
return OUT;
}
L'optimisation est petite, mais très fière.
Conclusion
L'aberration chromatique latérale elle-même semble très cool; ce défaut n'interfère pas avec la vue au centre. L'idée de décomposer la lumière en poids est une expérience très intéressante qui peut donner une image complètement différente si votre moteur ou jeu permet plus de trois échantillons. Dans notre cas, il était possible de ne pas s'embêter et de proposer un algorithme différent, car même avec des optimisations, nous ne pouvons pas nous permettre de nombreux échantillons et, par exemple, la différence entre 3 et 5 échantillons n'est pas très visible. Vous pouvez expérimenter vous-même la méthode décrite et voir les résultats.