💵 👰🏿 🙏🏿 Réseaux bayésiens avec Python - quoi et pourquoi? 👩🏽‍🎨 🥁 🔨

Avertissement: Cet article est une traduction adaptée. L'original peut être lu ici .

Réseaux bayésiens avec Python - expliqués avec des exemples

En raison des informations limitées (en particulier en russe natif) et des ressources de travail, les réseaux bayésiens sont entourés d'un certain nombre de problèmes. Et on pourrait bien dormir si elles n'étaient pas implémentées dans la plupart des technologies avancées de l'époque, telles que l'intelligence artificielle et l'apprentissage automatique.

Partant de ce fait, cet article est entièrement consacré au travail des réseaux bayésiens et à la façon dont ils ne peuvent pas eux-mêmes former de problèmes, mais être appliqués dans leur solution, même si les problèmes en cours de résolution sont extrêmement déroutants.

Structure de l'article

Qu'est-ce qu'un réseau bayésien?
Que sont les graphes acycliques dirigés?
Quels sont les mathématiques dans les réseaux bayésiens
Un exemple reflétant l'idée d'un réseau bayésien
L'essence du réseau bayésien
Réseau bayésien en Python
Application des réseaux bayésiens

Allons-y.

Qu'est-ce qu'un réseau bayésien?

Les réseaux bayésiens entrent dans la catégorie des modèles graphiques probabilistes (GPM). Les VGM sont utilisés pour calculer la variabilité à appliquer aux concepts de probabilité.

Le nom commun des réseaux bayésiens est Deep Networks. Ils sont utilisés pour modéliser des graphes acycliques dirigés.

Que sont les graphes acycliques dirigés?

Un graphe acyclique dirigé (comme tout graphe dans les statistiques) est une structure de nœuds et de liens, où les nœuds sont responsables de certaines valeurs et les liens reflètent les relations entre les nœuds.

Acyclique == n'ayant pas de cycles dirigés. Dans le contexte des graphes, cet adjectif signifie qu'en partant d'un chemin à partir d'un point, on ne parcourt pas le diagramme entier du graphe, mais seulement une partie de celui-ci. (C'est-à-dire, par exemple, si nous partons du nœud 2 dans l'image, nous n'irons certainement pas au nœud 1).

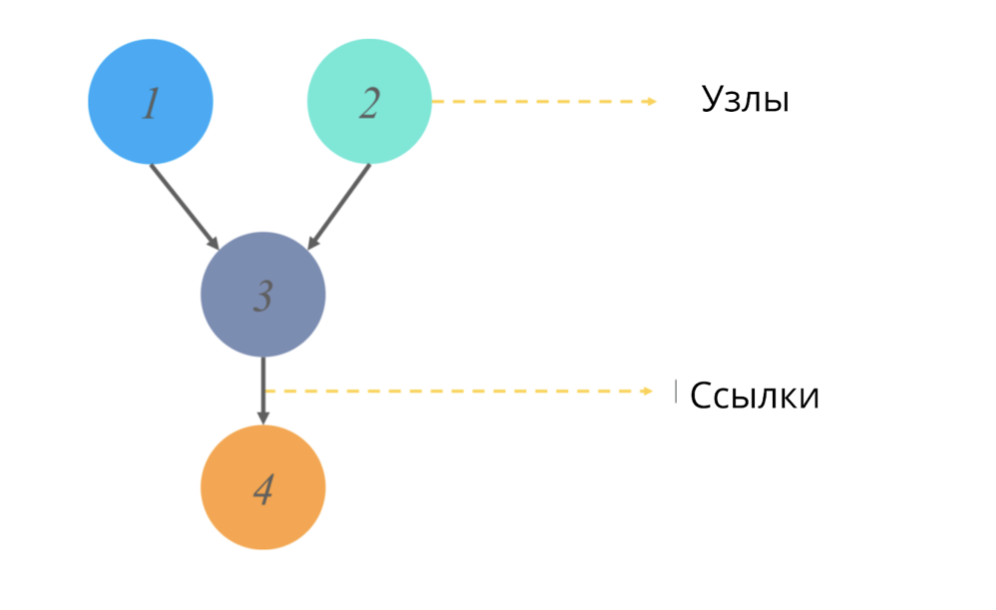
Que simulent ces graphiques et quelle valeur de sortie donnent-ils?

Les modèles de graphes orientés incertains sont également basés sur un changement de l'origine probabiliste d'un événement pour chacune des valeurs aléatoires. Une table de probabilité conditionnelle est applicable pour représenter et interpréter chaque valeur et ainsi nous pouvons simuler le branchement de la probabilité d'événements séquentiels.

Tout va bien. J'ai également été confus au début. Pour une meilleure compréhension, analysons la composante mathématique des réseaux bayésiens.

Mathématiques du réseau bayésien

Comme déjà mentionné dans la définition, les réseaux bayésiens sont basés sur la théorie des probabilités, par conséquent, avant de commencer à travailler avec des réseaux bayésiens, deux questions doivent être traitées:

Qu'est-ce que la probabilité conditionnelle?

Quelle est la distribution de probabilité moyenne conjointe?

Probabilité

conditionnelle La probabilité conditionnelle d'un événement X est la valeur numérique de la probabilité que l'événement X se produise, à condition qu'un événement Y se soit déjà produit.

La formule de probabilité standard pour une valeur (non donnée dans l'article): P (X) = n (x) / N, où n sont les événements étudiés et N sont tous les événements possibles.

Pour deux valeurs, les formules suivantes s'appliquent:

Si X et Y sont des événements dépendants:

P (X ou Y) = P (X ⋂ Y) / P (Y), l'intersection de la probabilité de X et Y / sur la probabilité Y. (Le signe «» dans le numérateur signifie l'intersection des probabilités)

Si les événements X et Y sont indépendants:

P (X ou Y) = P (X), c'est-à-dire que l'occurrence des événements à l'étude est également probable les uns aux autres.

Probabilité conjointe La probabilité

conjointe est la définition d'une mesure statistique pour deux événements ou plus se produisant en même temps. Autrement dit, les événements X, Y et, disons C, se produisent ensemble et nous reflétons leur probabilité cumulative en utilisant la valeur P (X ⋂ Y ⋂ C).

Comment cela fonctionne-t-il dans les réseaux bayésiens? Regardons un exemple.

Un exemple qui reflète l'essence du réseau bayésien

Disons que nous devons modéliser la probabilité d'obtenir l'une des notes d'un élève à un examen.

Le score est composé de:

Niveau de difficulté d'examen (e): variable discrète avec deux gradations (difficile, facile)
Student IQ: variable discrète avec deux gradations (faible, élevé)

La valeur d'évaluation qui en résulte sera utilisée comme un prédicteur (valeur prédictive) de la probabilité qu'un étudiant ou une étudiante entre à l'université.

Cependant, la variable IQ affectera également l'admission à l'admission.

Nous représentons toutes les valeurs à l'aide d'un graphe acyclique dirigé et d'une table de distribution de probabilité conditionnelle.

En utilisant cette représentation, nous pouvons calculer une probabilité cumulative, formée à partir du produit des probabilités conditionnelles de cinq variables.

Probabilité cumulative:

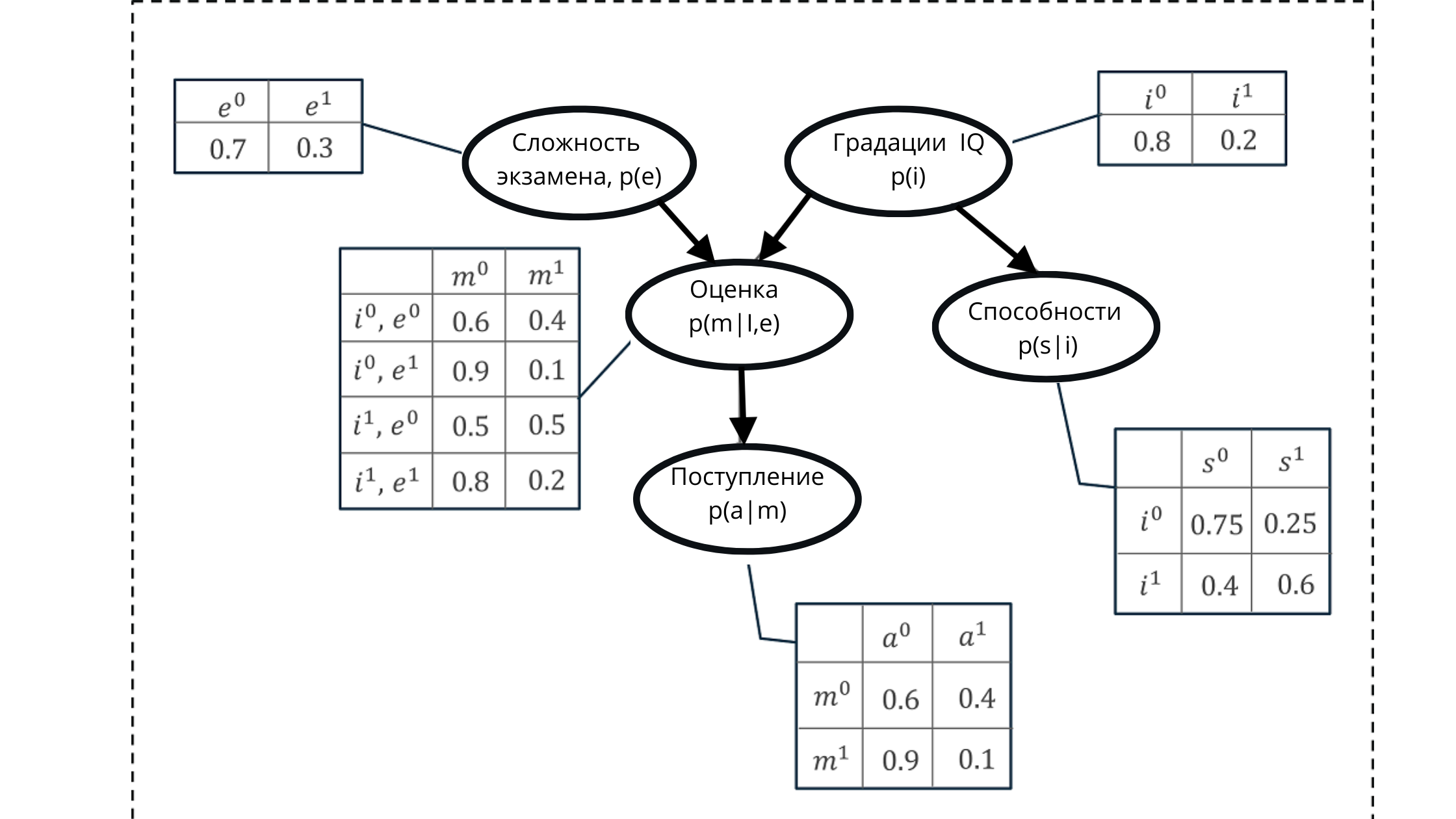
p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e) p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e)

$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$

Dans l'illustration:

p (e) est la distribution de probabilité pour les notes de la variable d'examen (affecte la note p (m | i, e)))

p (i) est la distribution de probabilité pour les notes de la variable IQ (affecte la note p (m | i, e )))

p (m | i, e) - distribution de probabilité pour les notes, en fonction du niveau de QI et de la difficulté de l'examen (dépend de p (i) et p (e))

p (s | i) - coefficients de probabilité pour les capacités des élèves , basée sur le niveau de son QI (dépend de la variable IQ p (i))

p (a | m) est la probabilité d'inscription d'un étudiant à l'université, basée sur ses estimations p (m | i, e)

Ici, je rappelle que la propriété d'un graphe acyclique est une réflexion relation. Dans la figure, nous pouvons clairement voir comment les nœuds parents affectent les enfants et comment les enfants dépendent des parents.

D'où la formulation de l'ensemble des valeurs générées à l'aide des réseaux bayésiens.

L'essence du réseau bayésien

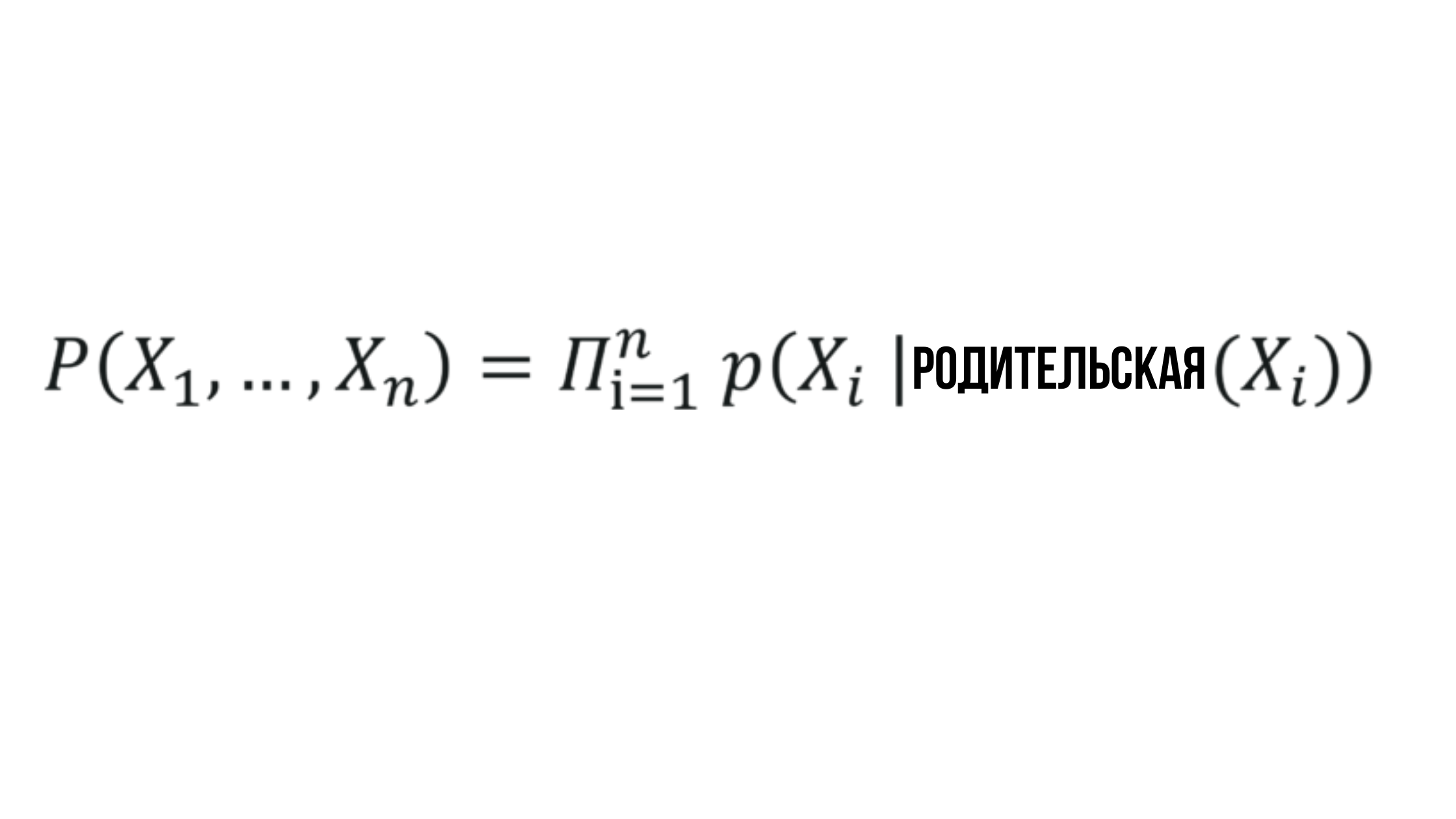
Où la probabilité X_i dépend de la probabilité du nœud parent correspondant et peut être représentée par n'importe quelle valeur aléatoire.

Cela semble simple, et à juste titre - les réseaux bayésiens sont l'une des méthodes les plus simples utilisées dans l'analyse descriptive, la modélisation prédictive, etc.

Réseau bayésien en Python

Examinons l'application d'un réseau bayésien à un problème appelé le paradoxe de Monty Hall.

En bout de ligne: imaginez que vous participez au format de mise à jour du jeu "Field of Miracles". Le tambour ne tourne plus - maintenant vous ne devriez pas appliquer votre F, mais jouer avec p.

Il y a trois portes devant vous, derrière lesquelles une voiture est également susceptible de se trouver. Les portes, derrière lesquelles il n'y a pas de voiture, vous mèneront aux chèvres.

Après avoir choisi, le chef du reste ouvre celle qui mène à la chèvre (par exemple, vous avez choisi la porte 1, ce qui signifie que le chef ouvre la porte 2 ou 3) et vous invite à changer votre choix.

Question: que faire?

Solution: initialement la probabilité de choisir une porte avec une voiture = 33%, et avec une chèvre = 66%.

Si vous touchez 33%, changer la porte entraîne une perte => chance de gagner == 33%
Si vous atteignez 66%, le changement conduit à une victoire => probabilité de gagner == 66%

Du point de vue de la logique mathématique, changer de porte globalement conduit à une victoire dans 66% de pour cent et à une perte dans 33%. Par conséquent, la bonne stratégie consiste à changer la porte.

Mais nous parlons de réseau ici, et il peut y avoir beaucoup de portes, nous allons donc transférer la solution sur le modèle.

Construisons un graphe acyclique dirigé avec trois nœuds:

Porte de prix (toujours avec une voiture)
Porte sélectionnable (avec une voiture ou avec une chèvre)
Porte ouvrable en cas 1 (toujours avec une chèvre)

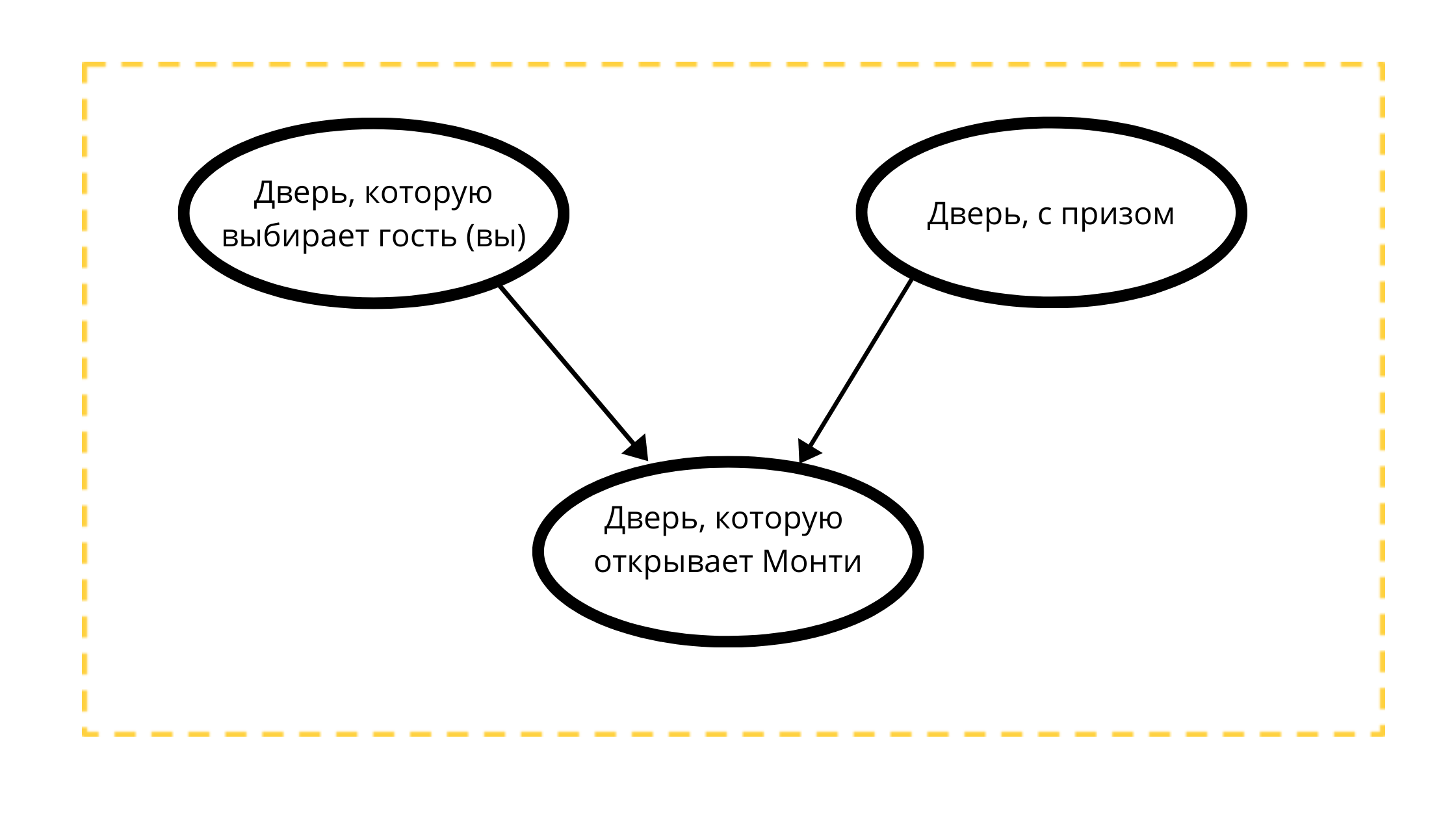
Lecture du décompte:

La porte que Monty va ouvrir est strictement influencée par deux variables:

La porte choisie par le client (vous) tk Monti 100% n'ouvrira PAS votre choix
Une porte avec un prix, peut-être que Monty ouvre toujours une porte sans prix.

Selon les conditions mathématiques de l'exemple classique, le prix peut être également placé derrière l'une des portes, tout comme vous pouvez également choisir n'importe quelle porte.

#   
import math
from pomegranate import *
 
#    "  " (   3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#    "   " (    )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#  ,       ,     
#    
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#  
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

Dans l'extrait de code, les valeurs sont:

A - la porte choisie par le client
B - prix porte
C - porte choisie par Monty

Sur le fragment, nous calculons la valeur de probabilité pour chacun des nœuds du graphe. Les deux nœuds supérieurs obéissent dans notre exemple à une distribution de probabilité égale et le troisième reflète la distribution dépendante. Par conséquent, afin de ne pas perdre de valeur, les probabilités de chacune des combinaisons possibles du jeu sont calculées pour .

Après avoir préparé les données, nous créons un réseau bayésien.

Il est important de noter ici qu'une des propriétés d'un tel réseau est de révéler l'influence des variables cachées sur les observables. Dans le même temps, ni les variables cachées ni les variables observables ne doivent être spécifiées ou déterminées à l'avance - le modèle lui-même examine l'influence des variables cachées et le fera avec plus de précision, plus il reçoit de variables.

Commençons à faire des prédictions.

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

Analysons le fragment en utilisant l'exemple de la variable A.

Supposons que l'invité l'ait choisi (A).

L'événement «il y a un prix derrière la porte» au stade du choix d'une porte par un invité a une distribution de probabilité == ⅓ (puisque chaque porte peut être également susceptible d'être un prix).

Ensuite, ajoutez la valeur des probabilités que la porte soit le prix au stade où Monty choisit la porte. Puisque nous ne savons pas si le prix de la porte a été exclu par notre propre choix (invité) à l'étape 1, la probabilité que la porte soit un prix à ce stade est de 50/50.

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

Dans cette étape, nous modifierons les valeurs d'entrée de notre réseau. Maintenant, cela fonctionne avec la distribution de probabilité obtenue aux étapes 1 et 2, où

les chances de gagner à la porte de notre choix n'ont pas changé (33%)
les chances de gagner le prix à la porte ouverte par Monty (B) ont été annulées
les chances d'être un prix à la porte, qui a été laissé sans surveillance, ont pris la valeur de 66%

Par conséquent, comme il a été conclu ci-dessus, la stratégie correcte de la part des invités pour ce jeu est de changer la porte - ceux qui changent la porte mathématiquement ont ⅔ chances de gagner contre ceux qui ne changeront pas la porte (⅓).

Dans l'exemple à trois nœuds, les calculs manuels suffisent sans aucun doute, mais avec une augmentation du nombre de variables, de nœuds et de facteurs d'influence, le réseau bayésien est capable de résoudre le problème de la valeur prédictive.

Application des réseaux bayésiens

1. Diagnostics:

prédiction de la maladie basée sur les symptômes
modélisation des symptômes de la maladie sous-jacente

2. Recherche sur Internet:

formation de résultats de recherche basés sur l'analyse du contexte utilisateur (intentions)

3. Classification des documents:

filtres anti-spam basés sur l'analyse du contexte
répartition de la documentation par catégorie / classe

4. Génie génétique

modélisation du comportement des réseaux de régulation génique en fonction des interconnexions et des relations des segments d'ADN

5. Produits pharmaceutiques:

surveillance et valeur prédictive des doses acceptables

Les exemples ci-dessus sont des faits. Pour une compréhension complète, il est pertinent d'imaginer à quel stade la création d'un réseau bayésien est connectée et en quels nœuds le graphe le décrivant.

Le problème du paradoxe de Monty Hall n'est qu'un fondement qui permet d'illustrer du bout des doigts le fonctionnement des chaînes basées sur une combinaison de distributions de probabilité dépendantes et indépendantes. J'espère que je l'ai compris.

PS Je ne suis pas un as de Python et j'apprends juste, donc je ne peux pas être responsable du code de l'auteur. La publication de cet article sur Habré poursuit plus de libération dans le monde du travail intellectuel de traduction. Je pense qu'à l'avenir, je serai en mesure de générer mes propres tutoriels - dans lesquels je serai déjà heureux de voir des pensées constructives sur le code.

Réseaux bayésiens avec Python - quoi et pourquoi?