Autres articles du cycle
Après une présentation détaillée avec des détails sur les transformations individuelles, avec des éléments d'un champ algébrique fini, non abstrait (comme dans de nombreuses publications, sans exclure le Khabrovsky), mais ( concret ), dans lequel RIJNDAEL, AES-128 et ( effectuer des opérations de la norme AES-128 ) sont implémentés , nous pouvons passer à l'examen d'éventuelles attaques sur le chiffrement. Pour l'instant, nous nous limiterons à une attaque, à notre avis, la plus compréhensible et la plus transparente (bien que peut-être pas à tous les lecteurs) Habr.
Je suis déjà habitué aux inconvénients, mais avec quoi le diable ne plaisante pas. L'analyse des attaques possibles et des résultats attendus a été réalisée par de nombreux auteurs, mais des exemples concrets de réussite ou des conceptions tout simplement impressionnantes ne suffisent manifestement pas. Ici, nous considérerons d'un point de vue mathématique une attaque utilisant une erreur introduite par l'intrus dans le texte chiffré. Lors du choix d'une attaque pour une démonstration, l'auteur a essayé de ne pas impliquer celles où des choses mathématiques trop tordues et abstruses sont utilisées, mais le sujet en question lui-même est assez sérieux et ne permet pas de passer aux explications sur les «doigts».
Un objectif important de la publication est de montrer l'application des mathématiques, qui forment la base de l'AES-128, et que, malheureusement, de nombreux auteurs contournent ou interprètent mal sans fondement et sans fondement, guidés par le fait que peu de gens peuvent vérifier et souligner leurs inventions.
Le contenu de l'article n'est pas complètement le concept original de l'attaque, les principales actions sont tirées du travail , mais il a été soigneusement élaboré, complété et testé expérimentalement par mes étudiants. Ils ont obtenu de bonnes pratiques à la fois en algèbre supérieure et en cryptologie.
1. Attaque de la clé de chiffrement AES
Tout d'abord, une attaque contre AES est décrite dans un cas simple, puis il devient clair comment une telle attaque peut être généralisée. Le but de l'attaque considérée est de récupérer la clé K (Nr) du chiffrement. Une fois la clé partielle (ronde) K (Nr) déterminée, il devient facile d'obtenir la clé K.
1.1 Principe d'attaque
On suppose qu'il est possible de changer en introduisant l'erreur "ε" dans un octet séparé de la matrice S de l'état (un de 16) après l'opération ShiftRows (Nr - 1), c'est-à-dire l'avant-dernier tour, et l'indice (# de la cellule) de l'octet corrompu (élément ) Etat. Cette dernière hypothèse peut être omise, elle a été introduite afin d'expliquer plus facilement le mécanisme d'attaque. La nouvelle valeur de l'élément d'état est supposée inconnue.
L'erreur "ε" ne s'étend pas à plus de quatre octets de l'état de sortie du processus. Pour les 4 éléments modifiables de l'état de sortie, un ensemble de valeurs (ensemble) de vecteurs d'erreur possible "ε" se trouve dans la section 1.4. De plus, il devient possible de croiser les ensembles de valeurs possibles "ε" (définition 1) pour ces quatre éléments. Lorsque de tels ensembles se croisent, un ensemble plus petit est obtenu, et ainsi le nombre de textes chiffrés requis pour une analyse complète est réduit.
Enfin, pour chaque erreur, nous imprimons quelques valeurs brouillées possibles pour les quatre éléments de la clé ronde précédente. Pour former d'autres textes chiffrés, nous trouvons quatre octets de la clé ronde K (10). Cette attaque reste réussie même avec de nombreuses hypothèses générales sur l'emplacement de l'erreur. Comme le manque d'informations sur l'emplacement de l'erreur avant la 9e transformation MixColumns (). La différence entre la matrice de texte chiffré avec et sans distorsions révélera les distorsions et leur position (dans l'exemple, ce sont les positions 0,7,10,13).
Il est également suggéré que les erreurs "ε" introduites au tour 8 (avant la 8e transformation MixColumns ()) pourraient être utiles pour l'analyse. Mais en même temps, le nombre de textes chiffrés requis pour une analyse plus complète augmente. Pour l'exemple numérique considéré, une dizaine de textes chiffrés sont nécessaires pour obtenir quatre octets de la clé ronde K (10), dans des conditions où l'hypothèse des emplacements d'erreur n'est pas considérée.
1.2 Exemple numérique de l'impact d'une erreur sur un message
Ici, le même exemple est utilisé comme indiqué dans l'annexe de l'ouvrage nommé . L'avant-dernier et le dernier cycle du processus de cryptage sont considérés (la représentation en octets des données a la forme):
Entrée = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';
Clé de chiffrement = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';
Sortie = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';
Erreur "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00'.
Le diagramme suivant montre les valeurs contenues dans les tableaux d'états en fonction de la longueur du bloc de chiffrement et de la longueur de la clé de chiffrement de 16 octets chacun (c'est-à-dire Nb = 4 et Nk = 4).
La propagation d'erreur est affichée en gras et en hexadécimal. Voici les carrés de l'État dans différentes situations:
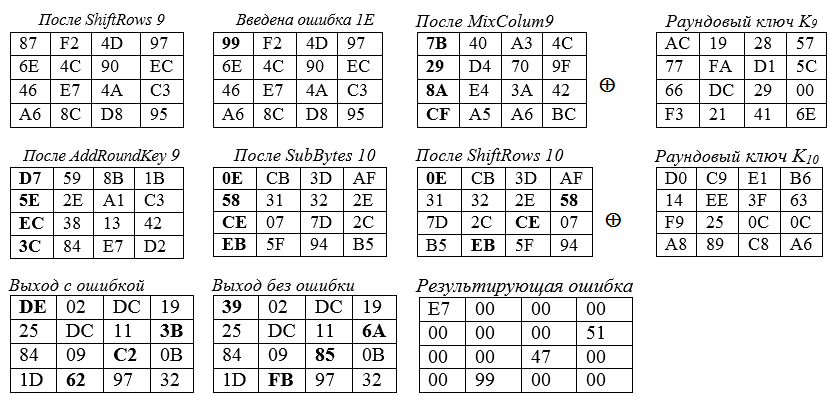
L'erreur "ε" = 1E, insérée dans le 0ème octet du 9ème état de tour, entraîne des changements dans les quatre octets de l'état final. Exemples de calculs pour les cellules d'angle de la diagonale principale du «carré» de l'état:
- l'erreur «ε» = 1E
87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
est entrée dans la cellule supérieure gauche (coin) du carré d'état du 9e tour - en bas à droite L'angle State du 9ème tour après MixColum9 se résume à l'octet clé K (9):
BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.
- calculer les valeurs de l'erreur résultante.
En présence de deux textes de message, avec et sans erreur, les valeurs et les positions des octets d'état corrompus sont déterminées en soustrayant un texte de l'autre. Dans notre cas, une telle soustraction peut être remplacée par la somme des textes modulo deux. Nous obtenons un résultat différent de zéro uniquement pour les octets modifiés par une erreur introduite dans le texte source.
Par exemple, sous forme hexadécimale, on retrouve les valeurs d'erreur:
Tableau 7 - calcul des valeurs d'erreur
En conséquence, les erreurs de différence... Donnons un exemple de calcul du dernier octet d'erreur:
62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.
Positions des octets d'état modifiés par l'erreur
.indiquent les indices des éléments de la clé ronde (dernier tour), comme K [0], K [7], K [10], K [13]. Ici, 0, 7, 10, 13 sont les numéros de cellule de la matrice d'état, et la matrice Ao est la matrice de transformation pour mélanger les colonnes du processus de cryptage, dont la première colonne a la forme: '02', '01', '01', '03'.
Comment une erreur injectée affecte l'état final final
Analyse des informations obtenues lorsqu'une erreur est introduite
La seule opération qui peut contenir des informations sur la clé K (Nr) est la dernière transformation SubBytes (). Par conséquent, nous avons quatre équations, où x0, x1, x2, x3, ε sont des variables inconnues.
Nous voulons trouver des solutions aux quatre équations suivantes:
Octets modifiés par une erreur contiennent des informations sur la clé inconnue qui a généré ces octets.
Toutes ces équations peuvent être généralisées en une seule équation
s (x + cε) + s (x) = ε ', (1)
où la valeur constante =' 01 ',' 02 'ou' 03 'et c'est cette équation que nous allons résoudre et analyser.
Définition 1 . L'ensemble des solutions de l'équation (1) pour les erreurs ε est désigné par le symbole B (cε ') et défini par l'expression:
B (cε') = S (cε ') = {ε є GF [2 8 ]: ∃ x є GF [2 8 ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.
Il s'agit d'une zone d'erreur individuelle correspondant à une erreur spécifique ε '. Pour les autres ε ', les zones d'erreur seront différentes.
Définition 2 . Considérons une transformation linéaire ℓ sur le champ GF (2):
ℓ: GF [2 8 ] → GF [2 8 ];
x → x 2 + x.
L'image de ℓ est une application de l'espace vectoriel Im (ℓ) GF (2), c'est-à-dire l'ensemble des éléments
(x 2 + x) de GF [2 8 ] on note 1 = Im (ℓ) et sa dimension dimGF (2) (E1) = 7. Si θ є 1, alors il existe deux solutions différentes x1, x2 є GF [ 2 8 ] équations x 2 + x = θ, et les solutions satisfont la relation x2 = x1 + 1 et x2 ∙ x1 = θ (modd φx, (2 8 -1)) par le théorème de Vieta.
La variable θ est un terme libre d'une équation quadratique
, illustrons la transformation linéaire considérée par un exemple.
Exemple Le champ GF est défini [2 8], la transformation x → x 2 + x est effectuée sur ses éléments .
Tableau 8 - le fragment initial du champ GF [2 8 ] et les résultats de la transformation des éléments.
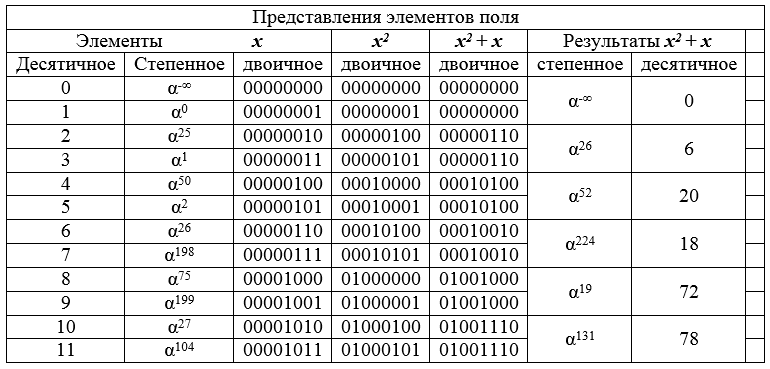
Le tableau 8 montre comment la conversion transforme les paires adjacentes d'une liste décimale en le même élément de champ. Il en résulte que le résultat de la transformation (image) est la moitié de la pré-image (le champ est, pour ainsi dire, compressé d'un facteur 2). Ce principe de contraction de la dimension des ensembles constitue la base de l'attaque proposée.
Proposition 2 . La déclaration suivante est vraie pour λ1, λ2 є GF [2 8 ] - {0}:
2. Généralisation et mise en œuvre
Tout d'abord, à l'aide d'une application logicielle spéciale, 20 textes chiffrés avec une erreur sont générés. Pour ce faire, le texte source, la clé, l'erreur sont saisis dans le modèle (programme) et le numéro de position dans lequel l'erreur est placée est défini. En appuyant sur le bouton "Démarrer", le programme implémente l'algorithme et affiche les résultats des 2 derniers cycles de cryptage sous forme développée pour le texte avec une erreur, le texte sans erreur et la différence entre eux. Après cela, le texte chiffré est enregistré sans erreur et avec une erreur. La valeur d'erreur est modifiée cycliquement et en appuyant sur le bouton "Démarrer", le texte chiffré suivant avec une erreur est obtenu. Sur une valeur de la colonne, 5 textes chiffrés avec une erreur ont été formés.
Pour mener une attaque, il est nécessaire d'ouvrir un fichier avec un texte chiffré sans erreur et un texte chiffré avec une erreur en utilisant le programme (les données du fichier sont présentées sous forme hexadécimale), les textes chiffrés et la différence entre eux sont affichés sous forme de tableau carré d'octets (State). En appuyant sur le bouton «Rechercher une clé», la procédure de recherche des octets possibles de la clé démarre. L'état actuel des processus est affiché dans une zone de texte. Après cela, un texte chiffré avec une autre erreur est ouvert et la procédure est répétée. Lorsqu'un octet clé rond de 10 est reçu, il est également affiché dans le tableau d'octets carrés correspondant. Lors de l'exécution des 20 textes chiffrés générés à l'étape précédente avec une erreur, il y a une forte probabilité d'obtenir les valeurs de tous les octets de la clé ronde 10 (sinon, des textes chiffrés avec des erreurs sont également nécessaires).Après cela, restaurez la clé de chiffrement selon l'algorithme «Récupération de la clé de chiffrement à l'aide de la dernière sous-clé» donnéici .
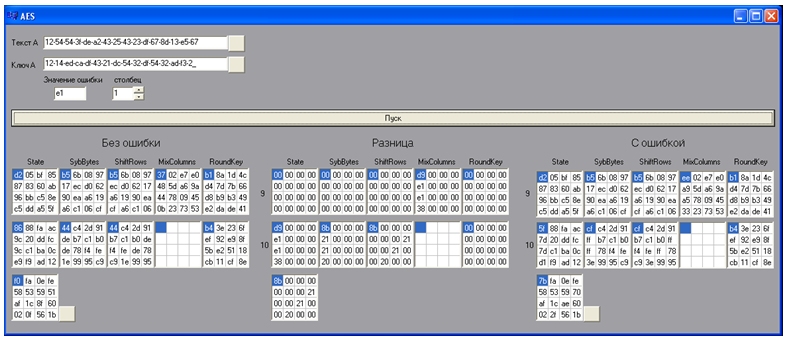
Figure 11 - Logiciel de construction d'un texte chiffré avec une erreur
Pour accélérer la procédure d'énumération des textes chiffrés avec une erreur, vous pouvez cocher le bouton "Rechercher la clé"
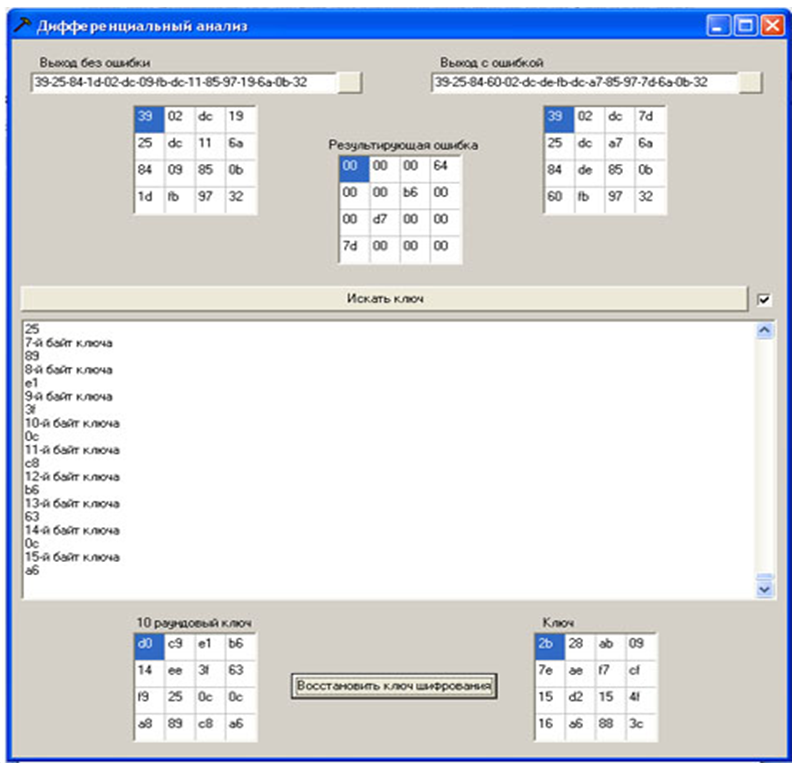
Figure 12 - Implémentation logicielle d'une attaque
Un exemple de produit logiciel:
Texte source 3243f6a8885a308d313198a2e0370734
Clé 2b7e151628aed2a6abf7158809cf4f3c
Erreur 1 1e000000000000000000000000000000
Texte chiffré avec erreur 1 Octets
possibles de25841d02bdc
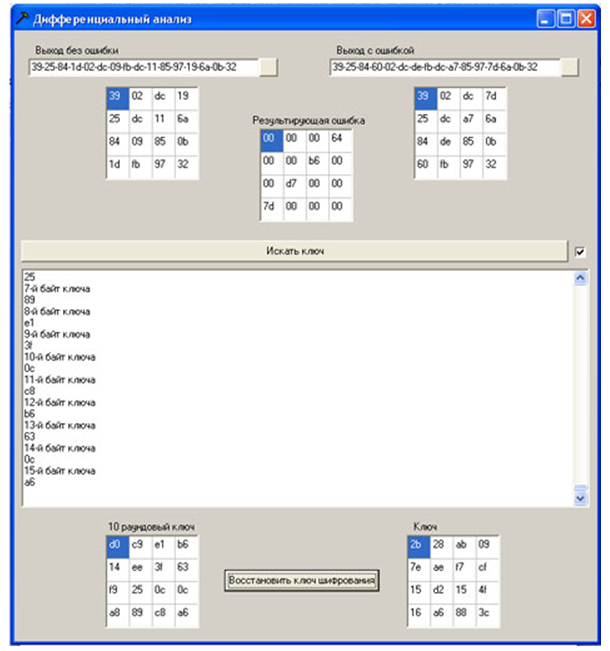
Figure 13 - Un exemple de l'opération du programme
Clé ronde 10 d014f9a8c9ee2589e13f0cc8b6630ca6 la clé est entièrement récupérée La
clé récupérée 2b7e151628aed2a6abf7158809cf4f3c, comme prévu, correspond à la clé spécifiée dans la session de chiffrement.
2.1. Situation où il n'y a pas d'informations de localisation d'erreur
À ce stade, on suppose que l'erreur est contenue dans l'octet d'état entre les deux dernières exécutions de l'opération MixColumns. C'est le même cas, quand précédemment, sauf que l'erreur peut être incluse entre les octets de 1 à 16. L'erreur est multipliée par l'opération MixColumns et se propage à 4 octets d'état.
Une erreur forcée est générée dans la première ligne de la matrice d'état différentiel. Ici, il est possible de déterminer à quelle colonne l'erreur saisie appartient en regardant la colonne d'erreur forcée. Ceci est fait en examinant les quatre positions de ligne possibles pour l'erreur saisie en utilisant la méthode décrite dans la description précédente.
2.2. Périphérique matériel
Supposons que vous ayez la capacité d'interférer physiquement avec un périphérique matériel AES. Tout d'abord, calculons les chiffrements pour plus de dix textes en clair aléatoires à l'aide d'un périphérique AES. Puis nous modifions l'exemple de projet en découpant les lignes et en les reliant au sol (ou Vcc) temporellement entre deux octets pendant le tour, situé deux tours avant la fin. Après tout, nous avons un octet dans le tour Nk -2, toujours remplacé par «00» (ou «FF»).
Nous calculons une autre fois le même message avec le dispositif agissant. Avec un texte brut aléatoire, un octet défectueux est comme une erreur aléatoire. Cette seule erreur se traduit par quatre erreurs dans la ronde Nk -1 et seize erreurs dans la ronde Nk. Dans ce cas, une matrice de déviation (différentielle) peut être obtenue, à l'aide de laquelle il est possible, en analysant l'erreur, de trouver la dernière clé ronde.
Littérature:
[1] FIPS PUB 197: Advanced Encryption Standard, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo et Lipton, On the Importance of Checking Cryptographic Protocols for Faults, Notes de cours en informatique, Advances in Cryptology, actes de EU-ROCRYPT'97, pp. 37-51, 1997.
[3] E. Biham et A. Shamir, Analyse différentielle des défauts des cryptosystèmes à clé secrète, CS 0910, Actes de Crypto'97.
[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance - a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, Californie, 18-21 novembre 1996, pp 1-11, ISBN 1-880446- 83-9.