Approximation linéaire d'une combinaison de lignes par un ensemble de points bruyants

Formulation du problème

Considérons le problème d'approximation d'une combinaison de lignes droites par un ensemble de coordonnées bruyantes de points situés sur une combinaison donnée de lignes (voir Fig. 1 et Fig. 2). La formule habituelle d'approximation linéaire ne fonctionnera pas ici, car les points sont mélangés et le résultat sera une ligne moyenne entre eux (voir Fig. 3).

Figure: 1 Combinaison de lignes et jeu de coordonnées bruyant

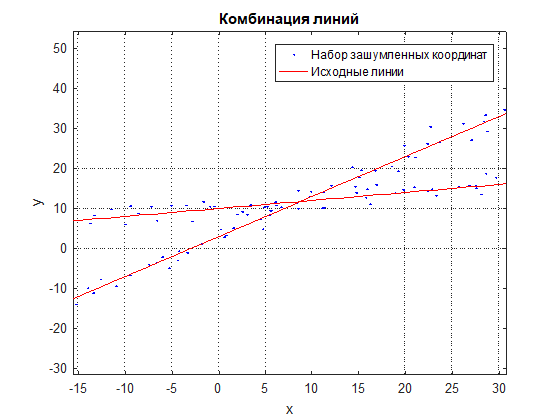
Figure: 2 Une combinaison de lignes et un ensemble de coordonnées bruyant à une échelle agrandie

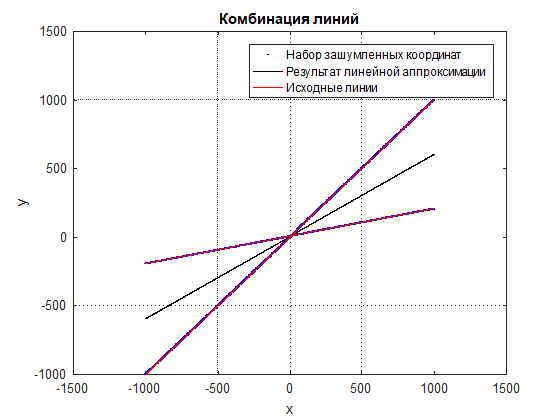
Figure: 3 Résultat de l'approximation linéaire

Algorithme

, , . .. , , -90 +90 ( -180 180 , .. ).

, , . , , . .

, , . , , .

1.

. , . , . -90 90 0.1 .

2.

, .

, , :

$$

$$y = kx + b, x_p, y_p$$

, , , :

$$

$$y-y_p=-(x-x_p)/k =>y= -x/k+ x_p/k+y_p$$

, :

$$

$$-x/k+ x_p/k+y_p=kx+b => -x+ x_p+ky_p= k^2 x+bk$$

$$

$$-bk+ x_p+ky_p= k^2 x+x => x= (x_p+ky_p-bk)/(k^2+1)$$

$$

$$y= k (x_p+ky_p-bk)/(k^2+1)+b= (〖kx〗_p+k^2 y_p-bk^2+bk^2+b)/(k^2+1)=(〖kx〗_p+k^2 y_p+b)/(k^2+1)$$

:

$$

$$dist= √((x_p- (x_p+ky_p-bk)/(k^2+1))^2+(y_p- (〖kx〗_p+k^2 y_p+b)/(k^2+1))^2 )$$

3.

, , , (. . 4-6).

. , (. . 7, 8). . 7 , .

. 4 ( )

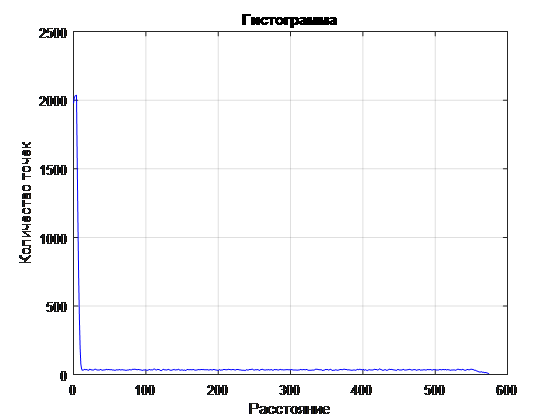
. 5 ( )

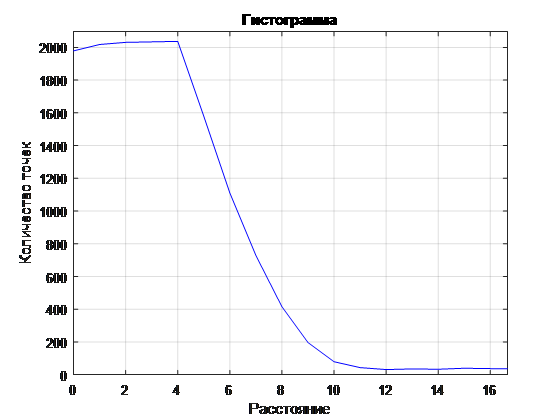
. 6 ( )

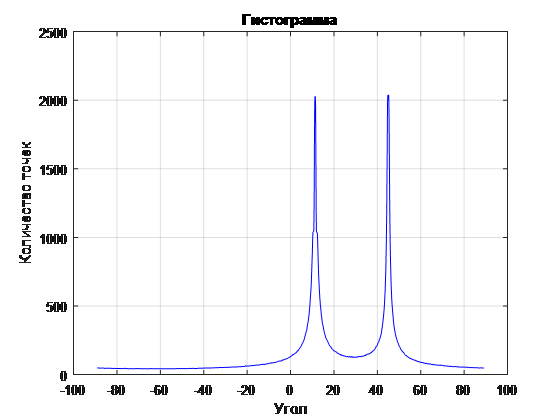
. 7 ( 1)

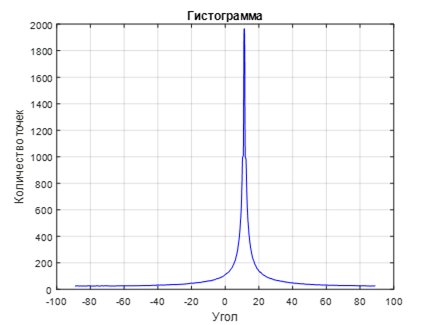
. 8 ( 2)

4.

, . , (. . 9 . 10):

$$

$$k= (N∑_1^N(xy)- ∑_1^Nx ∑_1^Ny)/(N∑_1^Nx^2 - (∑_1^Nx)^2 ); b =(∑_1^Ny-k∑_1^Nx)/N$$

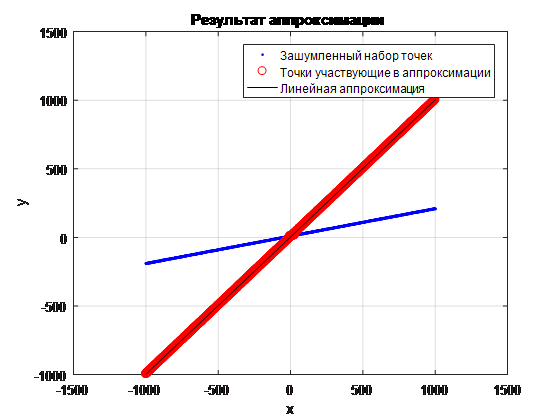
. 9

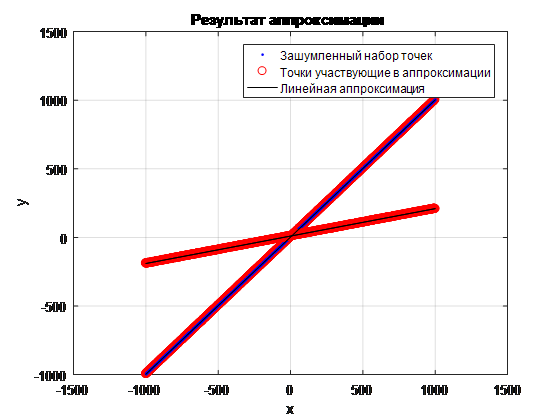
. 10

(. 11-13).

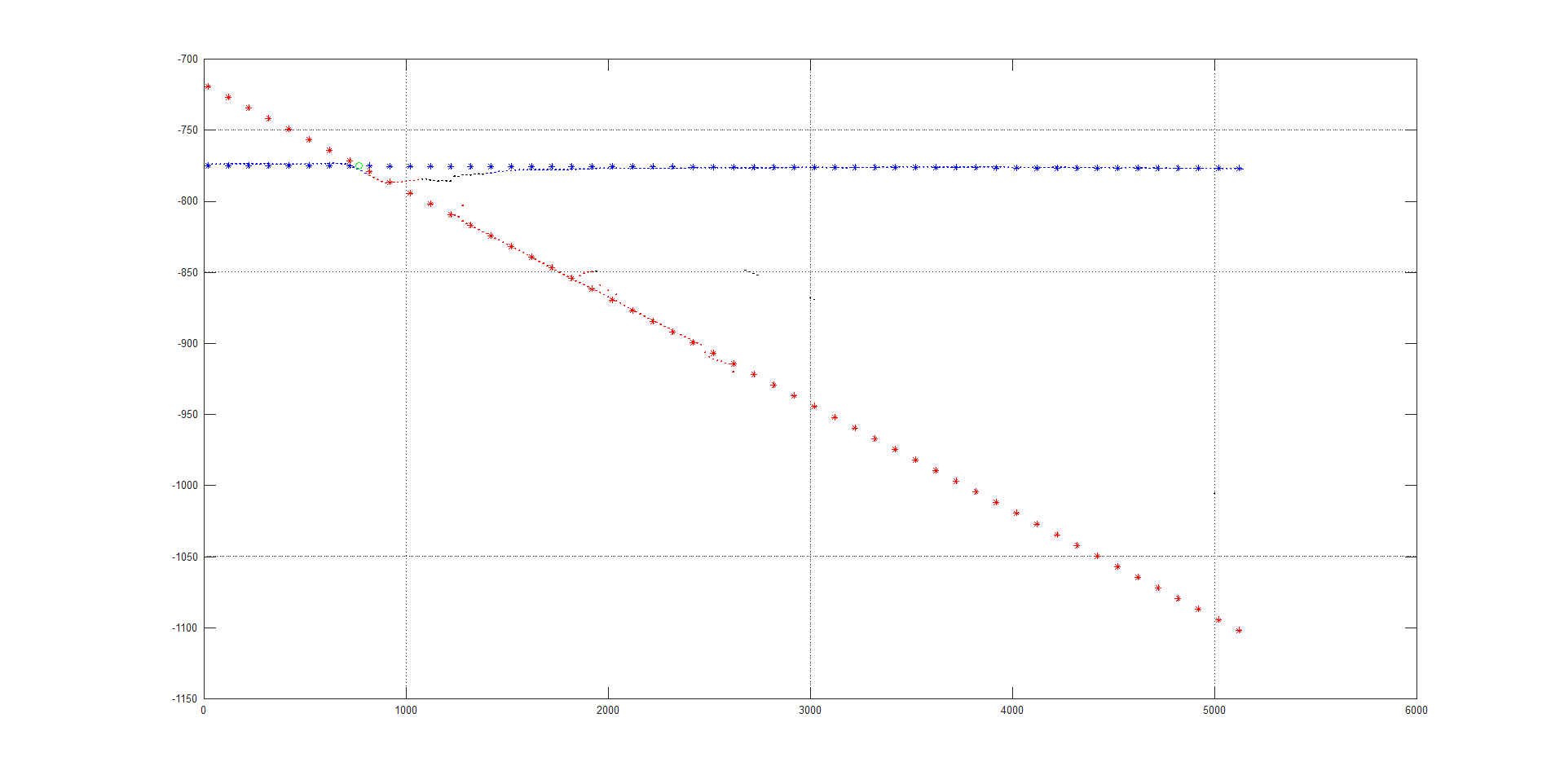
. 11

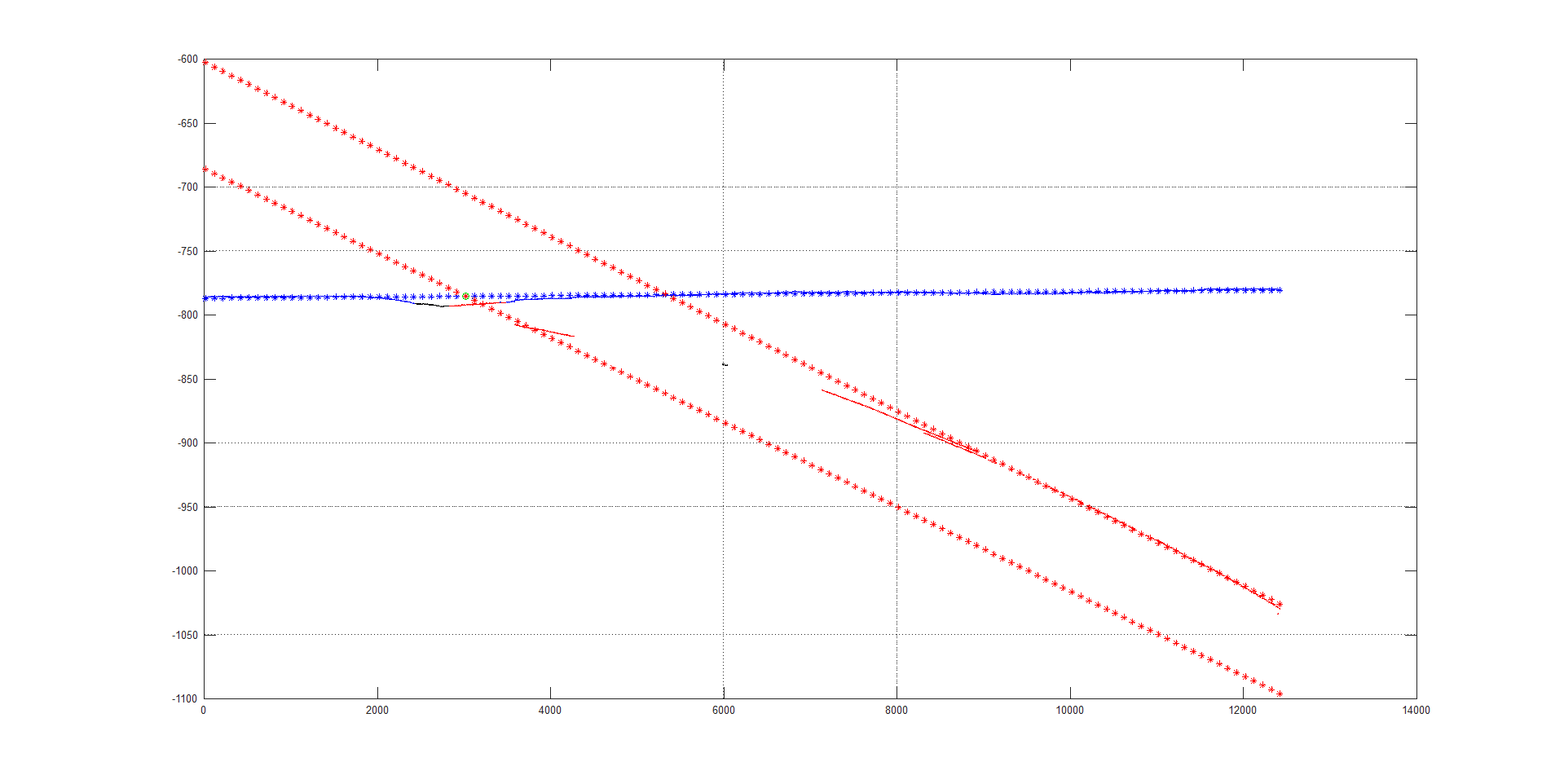
. 12

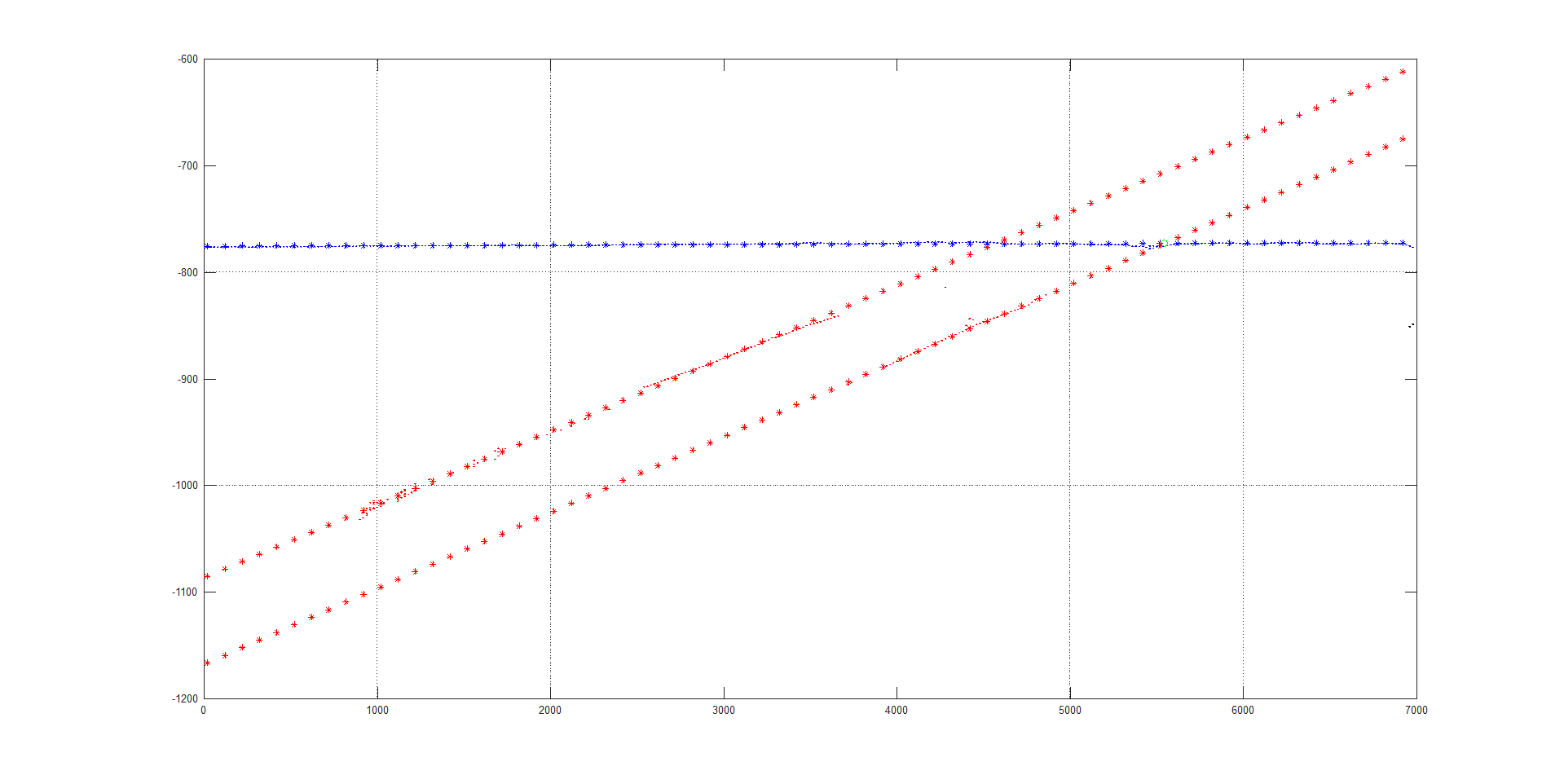
. 13

( ). .

, , , , .

, - . , . - , .