Dans cet article, vous apprendrez
- Qu'est-ce que CNN et comment ça marche
- Qu'est-ce qu'une carte des caractéristiques
- Qu'est-ce que la mise en commun maximale
- Fonctions de perte pour diverses tâches d'apprentissage en profondeur
Petite introduction
Cette série d'articles vise à fournir une compréhension intuitive du fonctionnement du deep learning, des tâches, des architectures réseau, des raisons pour lesquelles l'une est meilleure que l'autre. Il y aura peu de choses spécifiques dans l'esprit de «comment le mettre en œuvre». Entrer dans chaque détail rend le matériel trop complexe pour la plupart des publics. Le fonctionnement du graphe de calcul ou le fonctionnement de la rétropropagation à travers les couches convolutives a déjà été écrit. Et, surtout, il est bien mieux écrit que je ne l'expliquerais.
Dans l'article précédent, nous avons discuté de FCNN - ce que c'est et quels sont les problèmes. La solution à ces problèmes réside dans l'architecture des réseaux de neurones convolutifs.
Réseaux de neurones convolutifs (CNN)
Réseau neuronal convolutif. Cela ressemble à ceci (architecture vgg-16):
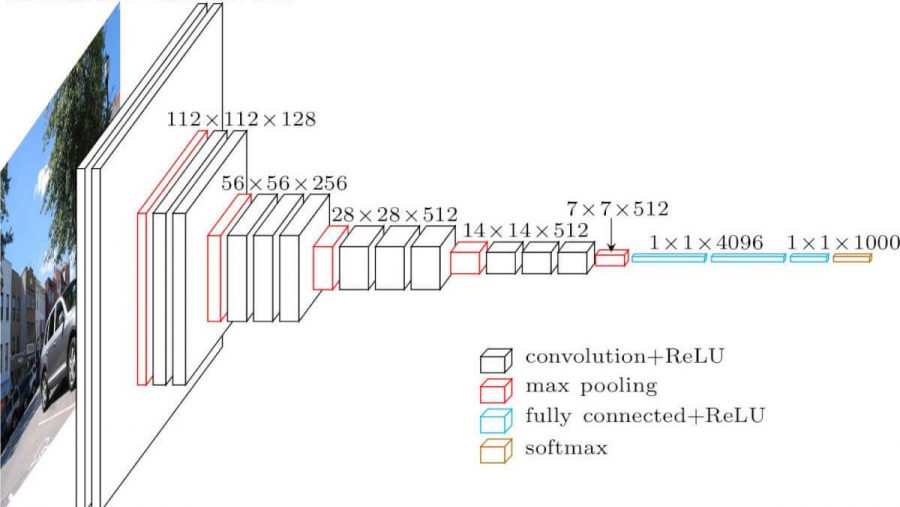
Quelles sont les différences avec un réseau entièrement maillé? Les couches cachées ont maintenant une opération de convolution.
Voici à quoi ressemble la convolution:

Nous prenons juste une image (pour l'instant - monocanal), prenons le noyau de convolution (matrice), composé de nos paramètres d'entraînement, "superposons" le noyau (généralement 3x3) sur l'image, et multiplions toutes les valeurs de pixels de l'image qui ont frappé le noyau. Ensuite, tout cela est résumé (vous devez également ajouter le paramètre de biais - offset), et nous obtenons un certain nombre. Ce numéro est l'élément de la couche de sortie. Nous déplaçons ce noyau sur notre image avec une certaine étape (pas) et obtenons les éléments suivants. Une nouvelle matrice est construite à partir de ces éléments et le noyau de convolution suivant lui est appliqué (après que la fonction d'activation lui a été appliquée). Dans le cas où l'image d'entrée est à trois canaux, le noyau de convolution est également à trois canaux - un filtre.
Mais tout n'est pas si simple ici. Les matrices que nous obtenons après la convolution sont appelées des cartes de caractéristiques, car elles stockent certaines caractéristiques des matrices précédentes, mais sous une autre forme. En pratique, plusieurs filtres de convolution sont utilisés à la fois. Ceci est fait afin d '"apporter" autant de fonctionnalités que possible à la couche de convolution suivante. Avec chaque couche de la convolution, nos caractéristiques, qui étaient dans l'image d'entrée, sont de plus en plus présentées sous des formes abstraites.
Quelques remarques supplémentaires:
- Après le pliage, notre carte des caractéristiques devient plus petite (en largeur et en hauteur). Parfois, afin de réduire plus faiblement la largeur et la hauteur, ou de ne pas la réduire du tout (même convolution), la méthode de remplissage à zéro est utilisée - remplissant avec des zéros "le long du contour" de la carte d'entités en entrée.
- Après la couche convolutionnelle la plus récente, les tâches de classification et de régression utilisent plusieurs couches entièrement connectées.
Pourquoi est-il meilleur que FCNN
- Nous pouvons maintenant avoir moins de paramètres entraînables entre les couches
- Désormais, lorsque nous extrayons des caractéristiques de l'image, nous prenons en compte non seulement un seul pixel, mais également les pixels proches (identifiant certains motifs dans l'image)
Mise en commun maximale
Cela ressemble à ceci:
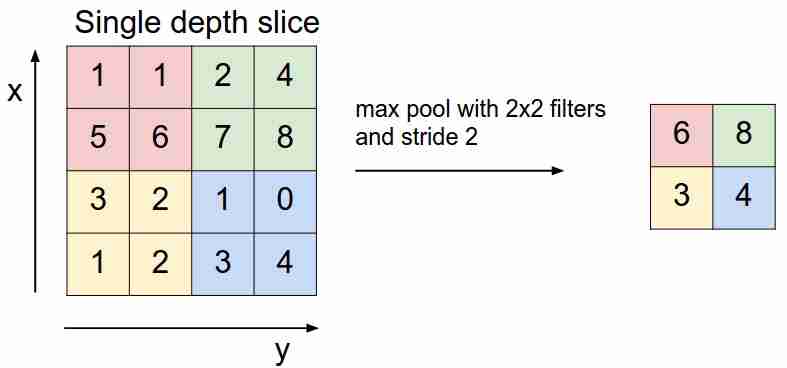
Nous "glissons" sur notre carte des caractéristiques avec un filtre et sélectionnons uniquement les caractéristiques les plus importantes (en termes de signal entrant, comme une certaine valeur), ce qui diminue la dimension de la carte des caractéristiques. Il y a aussi un pooling moyen (pondéré), lorsque nous faisons la moyenne des valeurs qui entrent dans le filtre, mais en pratique, c'est le pooling max qui est plus applicable.
- Cette couche n'a pas de paramètres entraînables
Fonctions de perte
Nous alimentons le réseau X à l'entrée, atteignons la sortie, calculons la valeur de la fonction de perte, exécutons l'algorithme de rétropropagation - c'est ainsi que les réseaux de neurones modernes apprennent (jusqu'à présent, nous ne parlons que d'apprentissage supervisé).
En fonction des tâches que les réseaux de neurones résolvent, différentes fonctions de perte sont utilisées:
- Problème de régression . Ils utilisent principalement la fonction d'erreur quadratique moyenne (MSE).
- Problème de classification . Ils utilisent principalement la perte d'entropie croisée.
Nous n'envisageons pas encore d'autres tâches - cela sera discuté dans les articles suivants. Pourquoi exactement de telles fonctions pour de telles tâches? Ici, vous devez entrer l'estimation du maximum de vraisemblance et les mathématiques. Peu importe - j'ai écrit à ce sujet ici .
Conclusion
Je veux également attirer votre attention sur deux choses utilisées dans les architectures de réseaux neuronaux, y compris les architectures convolutives: le décrochage (vous pouvez le lire ici ) et la normalisation par lots . Je recommande vivement la lecture.
Dans le prochain article, nous analyserons l'architecture CNN, nous comprendrons pourquoi l'une est meilleure que l'autre.