Comparaison de différentes méthodes de fusion de deux listes triées

Supposons que nous ayons deux listes (pour simplifier les nombres entiers), dont chacune est triée. Nous voulons les combiner en une seule liste, qui doit également être triée. Cette tâche est probablement familière à tout le monde; elle est utilisée, par exemple, dans le tri par fusion.

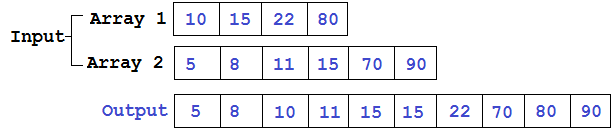
Il existe de nombreuses manières d'implémentation (notamment en python). Jetons un coup d'œil à certains d'entre eux et comparons le temps écoulé pour différentes entrées.

L'idée principale de l'algorithme est qu'en plaçant une étiquette au début de chaque liste, nous comparerons les éléments marqués, prendrons le plus petit d'entre eux et déplacerons l'étiquette de sa liste vers le numéro suivant. Lorsque l'une des listes se termine, vous devez ajouter le reste de la seconde à la fin.

Les données d'entrée ne changent pas

Soit deux listes list1et list2.

Commençons par l'algorithme le plus simple: marquons les étiquettes pour iet jet prenons la plus petite list1[i], list2[j]et augmentons son étiquette de un jusqu'à ce que l'une des étiquettes dépasse la limite de la liste.

, . , .

:

def simple_merge(list1, list2):
    i, j = 0, 0
    res = []
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            res.append(list1[i])
            i += 1
        else:
            res.append(list2[j])
            j += 1
    res += list1[i:]
    res += list2[j:] 
    #   list1[i:]  list2[j:]   ,     
    return res

, . . .

, . , , , , .

def iter_merge(list1, list2):
    result, it1, it2 = [], iter(list1), iter(list2)
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            result.append(el2)
            el2 = next(it2, None)
        else:
            result.append(el1)
            el1 = next(it1, None)
    return result

(result.append()) , . , , .

def gen_merge_inner(it1, it2):
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            yield el2
            el2 = next(it2, None)
        else:
            yield el1
            el1 = next(it1, None)

def gen_merge(list1, list2):
    return list(gen_merge_inner(iter(list1), iter(list2))) #    

python .

• merge heapq. , , , : , , .

  
  
  

  :

  
  
  

  from heapq import merge
  
  def heapq_merge(list1, list2):
  return list(merge(list1, list2)) #   

  
  
  

• Counter collections. Counter , , , , (, ).

  
  
  

  gen_merge_inner Counter(list1) Counter(list2):

  
  
  

  def counter_merge(list1, list2):
  return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))

  
  
  

• , , . .

  
  
  

  def sort_merge(list1, list2):
  return sorted(list1 + list2)

  
  
  

, ( ). . pop(0) , .

def pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[0] < list2[0] else list2).pop(0))
    return result + list1 + list2

4 , . , , . , . , , .

def reverse_pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1))
    return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]

.

, :

• simple_merge
• iter_merge
• gen_merge
• heapq_merge
• counter_merge
• sort_merge
• pop_merge
• reverse_pop_merge

timeit. .

: , , , , . .

, $$$1$ $$$10^5$, $$$1$ $$$10^6$.

pop reverse_pop:

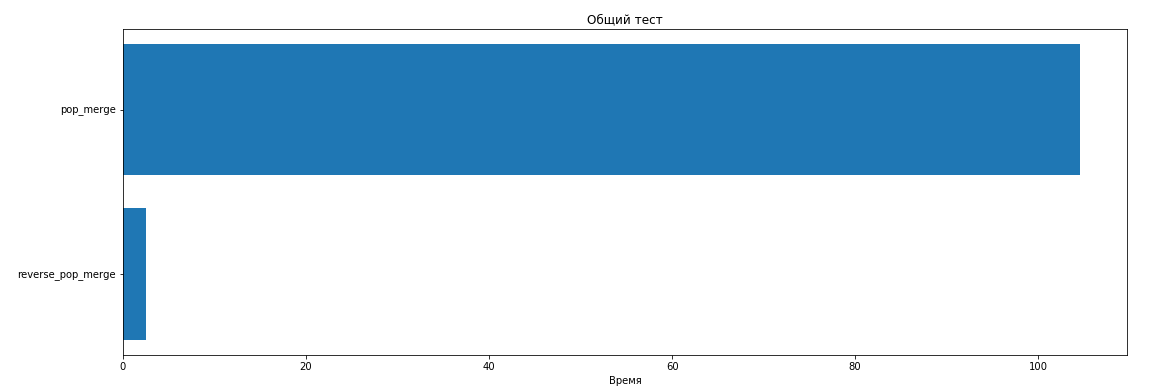
pop_merge , .

pop_merge, :

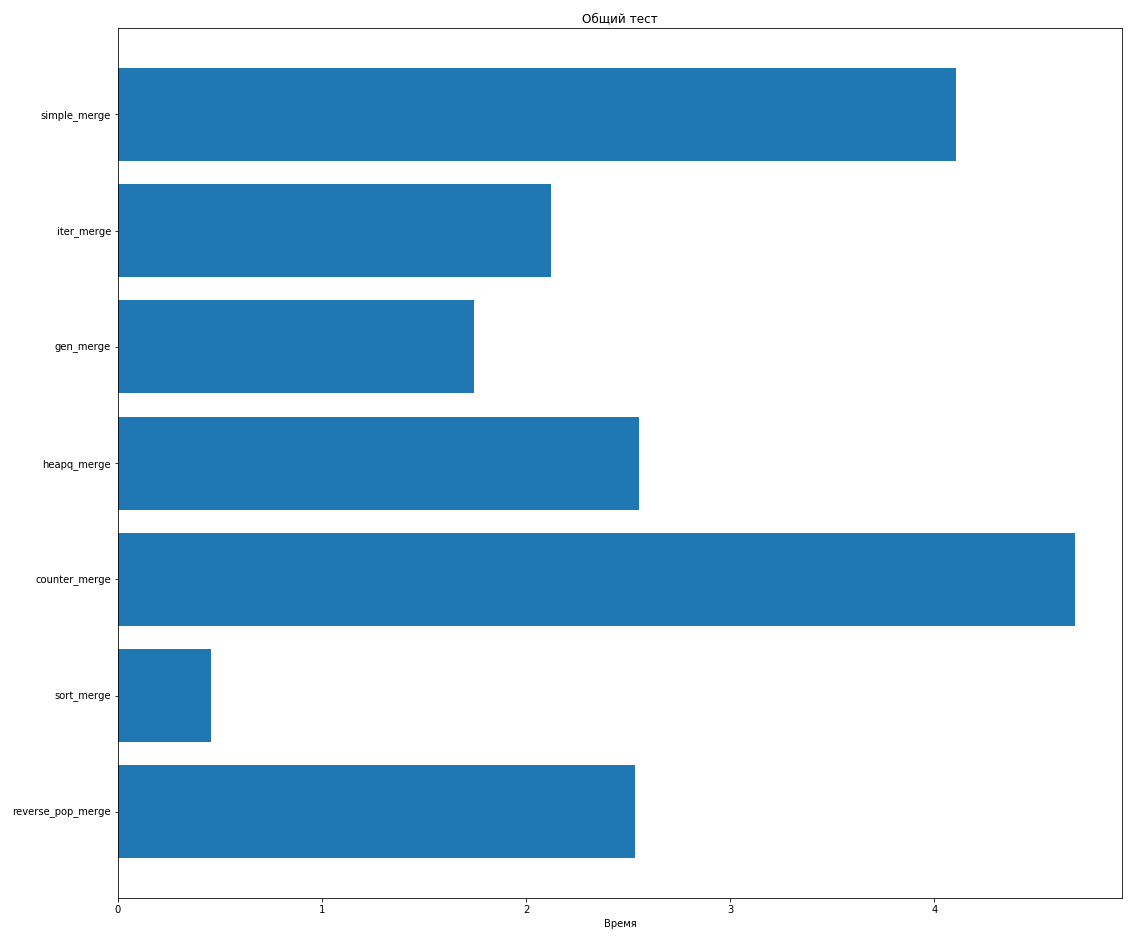
reverse_pop_merge heapq_merge.

, , , .

,

$$$[50x, 50(x+1))$, $$$x$ , $$$1$. $$$50$.

pop_merge heapq_merge, .

, ,

$$$x$, $$$10^4 + 100x$.

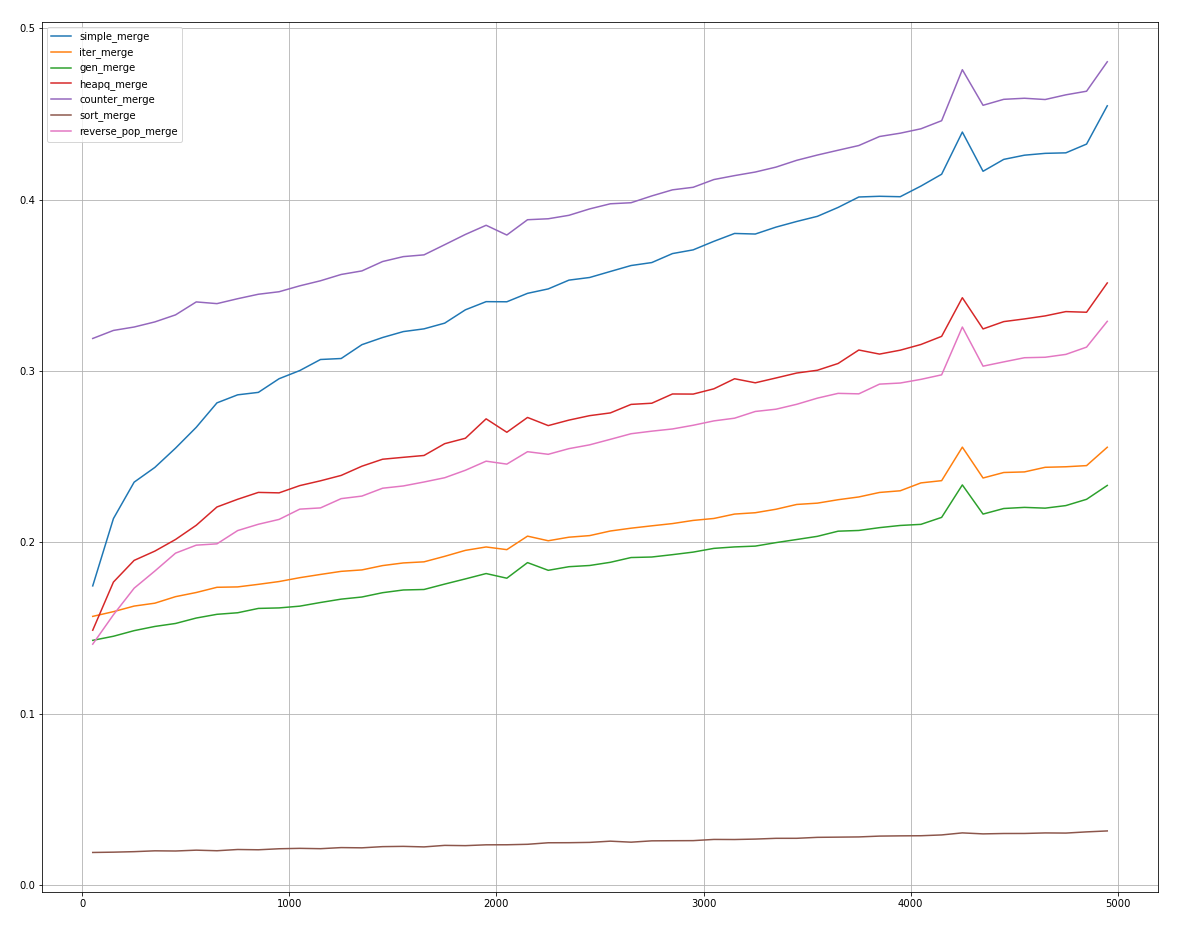
( ) reverse_pop_merge , sort_merge, .

,

, $$$5$, $$$1$.

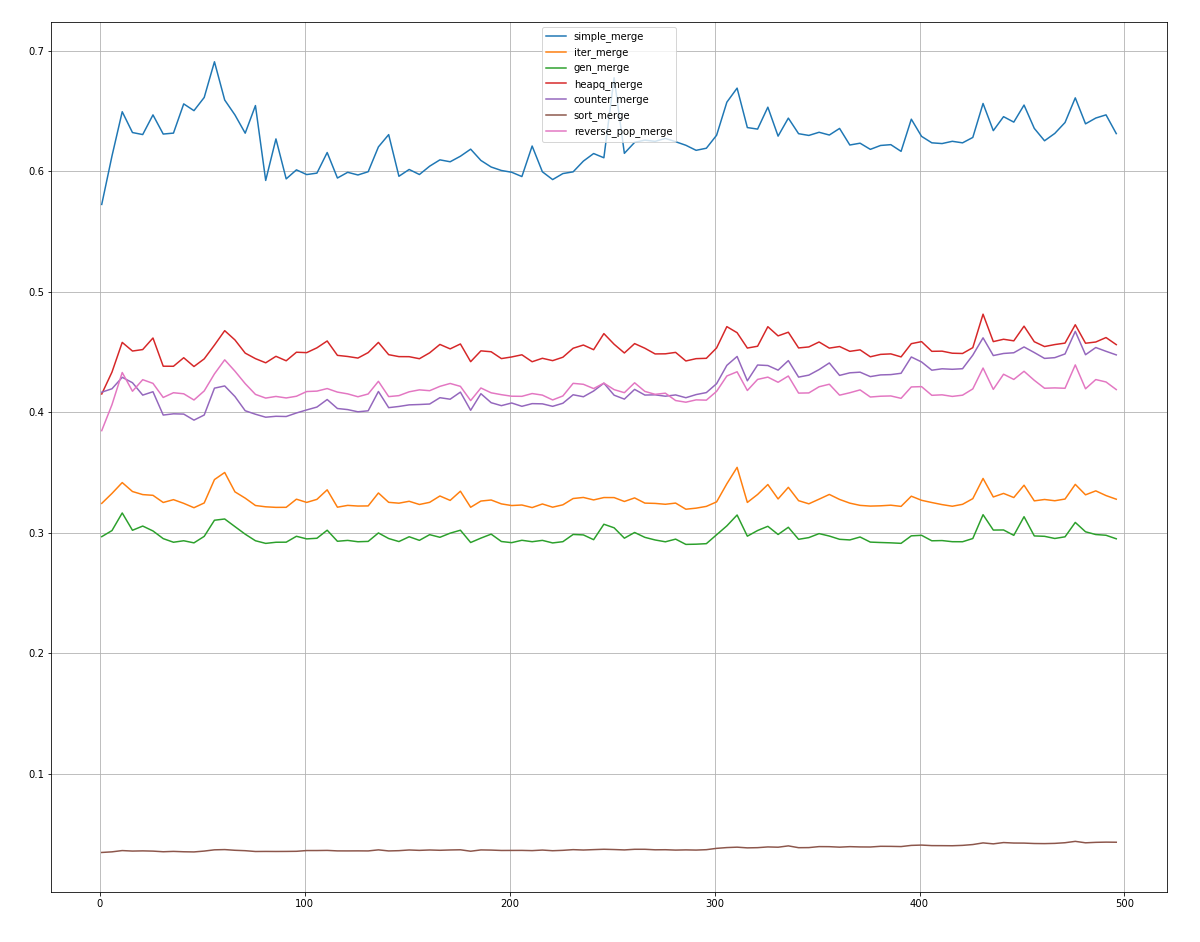
, counter_merge reverse_pop_merge heapq_merge, .

sort_merge! , .

En second lieu, dans la très grande majorité des cas, vient gen_merge, suivi de iter_merge.

Les autres méthodes prennent encore plus de temps, mais certaines, dans certains cas extrêmes, obtiennent des résultats de 2 à 3 places.

PS

Code, tests, notebook jupyter avec graphiques peuvent être trouvés sur gitlab .

Peut-être que cette analyse est incomplète, je serai heureux d'ajouter vos options à la comparaison, suggère.