Qu'est-ce que la musique en termes de mathématiques? Qu'est-ce que "la" ou "mi"? La manière exacte dont les sons sont formés est bien comprise à la guitare.
Son "mi" (son libre de la 1ère corde), son "la" ( 1ère corde serrée à la 5ème case ). "La" est de 440 Hz. Que signifie 440 Hz? C'est 440 fois la corde vibre par seconde. Le son "mi" est 5 demi-tons plus bas que le son "la" ( serré à la 5e frette ).

Encore 7 demi-tons plus bas, j'aurai à nouveau "mi", c'est-à-dire octave. Pourquoi le son libre de la première corde et le son de la corde serrée à la 12e case sont-ils appelés le même mot «mi»?

Il nous semble que la même note est jouée. Le fait est que la longueur de la corde à ce point ( "mi" à la 12e case ) est divisée exactement en deux:
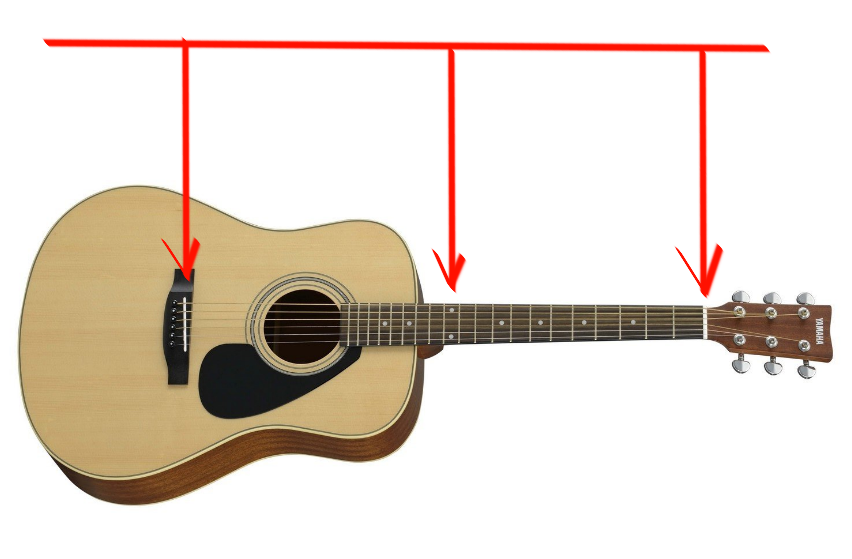
cela signifie que les vibrations de ce reste de la corde, selon les lois de la physique, seront deux fois plus fréquentes que les vibrations d'une corde complète.
Chaque fois que je redescends la corde et que je la serre à la frette suivante (la division indiquée par la ligne perpendiculaire sur le manche ), le son monte d'un demi-ton, comme disent les musiciens.
Notez que les frettes sur le manche sont de largeurs différentes. Ils diminuent progressivement, car pour augmenter la fréquence d'un demi-ton, il faut réduire la longueur de la corde d'un certain nombre de fois.
À quoi est-ce que je fais allusion en me concentrant sur le fait que quelque chose «sur» est traduit en quelque chose «dans»? Les mathématiciens diraient qu'il n'y a qu'une seule fonction (sous certaines conditions) où + va vers x ( multiplier ). Et cette fonction s'appelle le logarithme.
Cela signifie que nos oreilles, raccourcissant la corde et élevant le son un certain nombre de fois, sont perçues comme soulevant un demi-ton. Autrement dit, chaque frette raccourcit la corde du même nombre de fois, et nos oreilles disent que nous montons d'un demi-ton, atteignant la note «E» et recevant une octave. Nos organes auditifs sont logarithmiques.
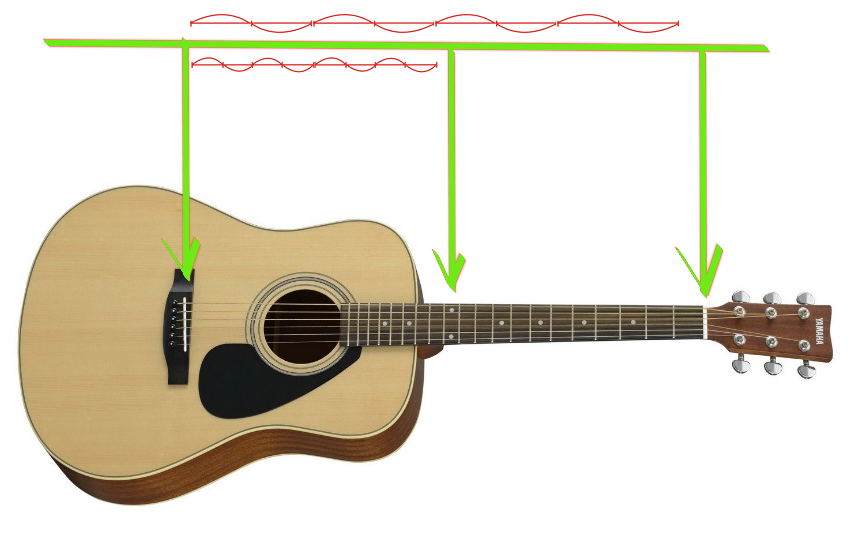
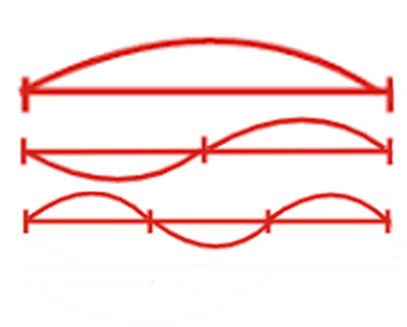
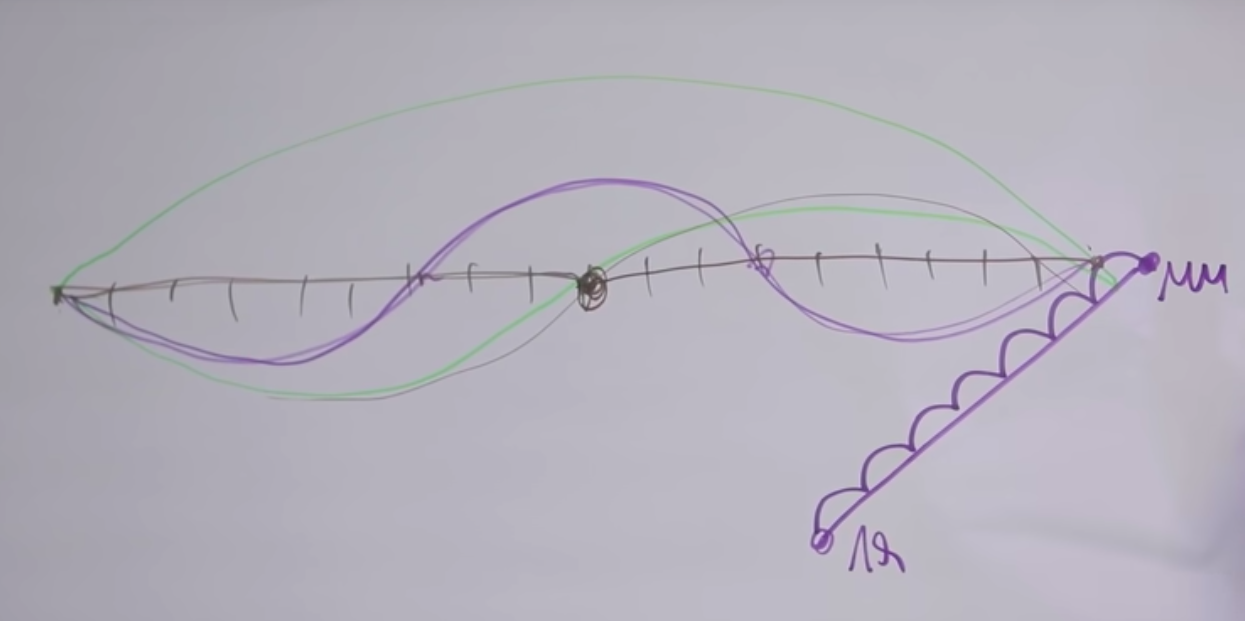
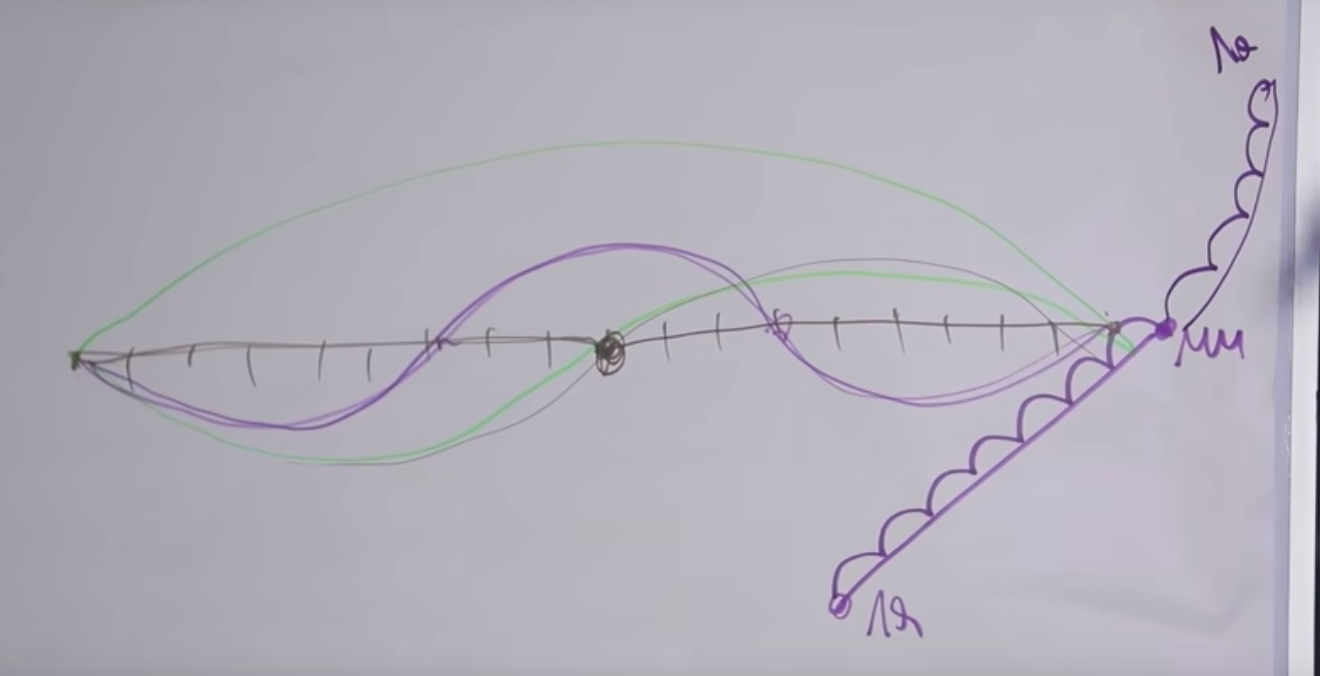
On dit que "mi" et "mi" sont deux fois différents, cela se voit à partir du son. L'arc supérieur bat son plein. Lorsque nous la serrons au milieu, la corde commence à vibrer, comme dans le graphique du milieu.
Pourquoi les sons sont-ils similaires? Le fait est qu'en même temps que la vibration principale de la corde, en fait, la vibration de la même corde se produit, à toutes les fréquences, où la longueur de la section vibratoire est inversement proportionnelle à la fréquence.
En conséquence, si la longueur diminue d'un nombre entier de fois, alors la tonalité correspondante peut être entendue. L'harmonique correspondante est réalisée par la chaîne donnée. Si une corde donnée vibre partiellement fixée à ces deux points ( graphique du bas ), alors sa tonalité sera trois fois plus élevée.
Une double augmentation de fréquence est perçue par l'oreille comme la même note. Toutes les harmoniques que nous divisons plusieurs fois, c'est-à-dire toute division d'un demi-segment est à la fois une division automatique et un grand segment. Et seules certaines divisions d'un grand segment ne rentrent pas dans le schéma de demi-division.
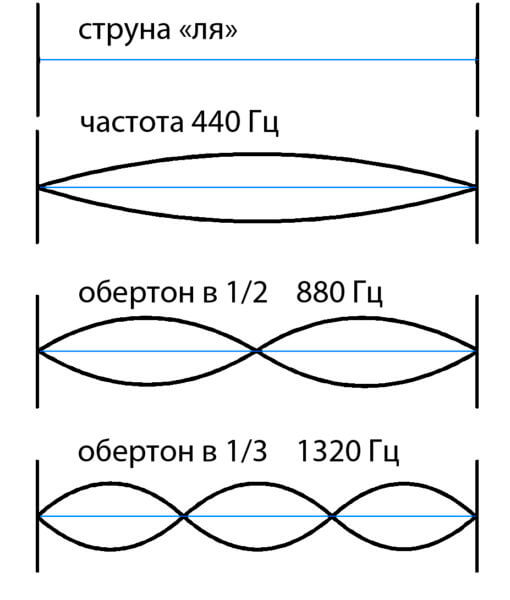
Si nous prenons les sons supérieurs pairs pour une longue corde, alors ils seront les sons supérieurs pour une corde à moitié raccourcie. Et absolument tout son raccourci d'une corde courte sonnera pendant une longue. Par conséquent, nous sentons que tout ce que nous entendons coïncide à ces points, et nous le percevons comme une note.
Il est encore plus intéressant qu'il y ait des notes qui passent par plusieurs demi-tons, et elles sont perçues par les oreilles comme une consonance, un accord, quelque chose qui plaît à l'oreille, ne nous coupe pas les oreilles. Quelles sont ces notes?
Si vous prenez 7 demi-tons, prenez la note "A" et augmentez le son de 7 demi-tons, jusqu'au prochain "E", alors ces deux notes sonneront bien.
Si vous reculez encore de 5 demi-tons, alors il y aura un "la" supérieur de l'octave suivante. Pour une raison quelconque, cet intervalle nous semble également agréable. Voyons tout cela.
Tout d'abord, si une augmentation de 1 demi-ton est une augmentation de la fréquence des oscillations d'un certain nombre de fois, alors nous la désignerons par x. Si vous avez besoin d'augmenter d'un demi-ton de plus, il y aura déjà x * x, c'est-à-dire x 2 . Si je l'ai augmenté de 12 demi-tons (x 12 ), alors il devrait augmenter exactement 2 fois. Nous obtenons l'équation x 12 = 2.
Par conséquent, une augmentation de 1 demi-ton signifie une contraction de la corde à x = 12√2, ou, ce qui est le même, augmenter la fréquence du son de 12 √2.
Et qu'est-ce que "la" et "mi" ont à voir avec cela? Pourquoi 7 demi-tons sont-ils mélodiques? Augmentons le degré:
Qu'est-ce qui est si agréable, bon dans ce nombre?
Parfois dans l'antiquité, des claviers tempérés, un enregistrement précis de la musique, ont été inventés. Vous pouvez le voir très bien sur la guitare, vous pouvez aussi le trouver sur le piano, il est caché à l'intérieur, si vous regardez à l'intérieur, vous pouvez voir les cordes.
Maintenant, ce nombre est très proche de 3/2. Si vous calculez sur une calculatrice, ce sera très précis. Cela signifie que "mi" est environ 1,5 fois plus élevé que le "la" précédent. Ceux. lever 7 tons équivaut à monter 3/2 fois, ce qui signifie que nous avons beaucoup d'harmoniques supérieures identiques.
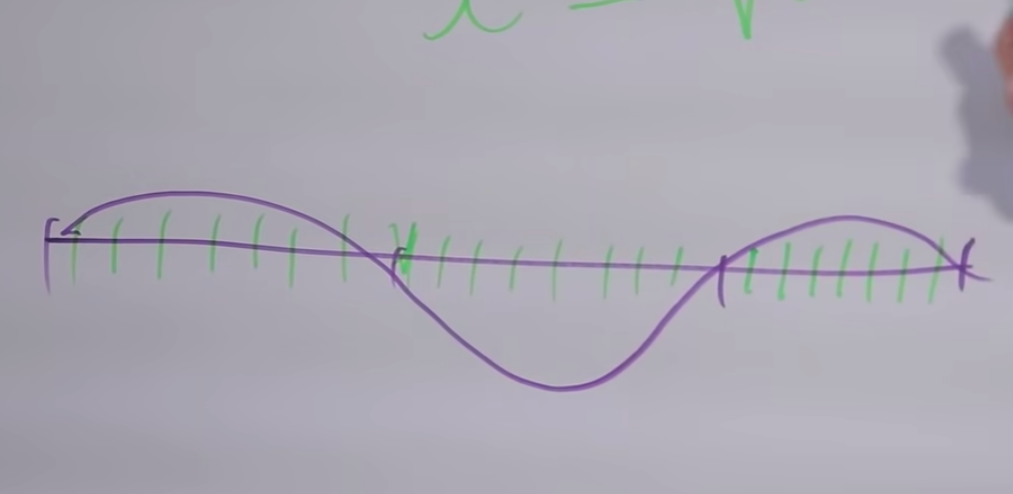
Parce que toute division par un entier d'un petit segment sera une division entière du segment entier. Et, en conséquence, diviser la coupe originale par le nombre de pièces, un multiple de trois, sera la division du petit segment (⅓), et ⅔ aussi. Lorsque nous avons quitté ⅔ de la longueur, c'est-à-dire augmenté la fréquence à 3/2, nous sommes montés d'environ 7 demi-tons, nous aurons de nombreuses harmoniques communes, ce sera une consonance agréable.
Les 4/3 restants sont exactement les 5 demi-tons restants, 3/2 x 4/3 = 2, juste une octave. Ce qui correspond à la formule x71243. La valeur est très proche de 4/3, mais pas de 100%. Ce nombre est irrationnel, ne peut pas être écrit comme une fraction, il ne peut pas être écrit comme un entier divisé par un entier.
J'ai entendu dire qu'il existe un instrument en Inde ( sitar), dans laquelle l'octave est divisée en 19 parties, c'est-à-dire ils ont un demi-ton = 1/19 octave, 19x2.

Et déjà avec une grande précision x121932, ce qui signifie que si sur un tel instrument indien vous reculez de 12 segments sur 19, il y aura plus d'harmoniques dans cette consonance, et cet intervalle sonne comme un baume pour les oreilles.
Il y a beaucoup de choses intéressantes à dire sur la musique et les mathématiques. En particulier, un accord majeur est perçu si 4 demi-tons sont ajoutés à une note initiale, puis 3, c'est-à-dire 0 - 4 - 3. Un mineur, si vous ajoutez 3 au début, puis 4, c'est-à-dire 0 - 3 - 4. La première et la dernière des trois notes de l'accord seront "les mêmes", elles diffèrent juste de 7 demi-tons, mais le son du milieu créera notre perception de consonance et s'accordera en mode mineur ou majeur.
Il semblerait que musique et mathématiques, que peut-il y avoir de commun? Et il y a tellement de points communs que les mathématiciens et les musiciens communiquent souvent, de plus, les mathématiciens comprennent facilement les musiciens, pour ainsi dire, ils saisissent un demi-ton.
Plusieurs liens utiles: