introduction
Cet article décrit un algorithme de tri de fusion adaptatif non récursif stable appelé quadsort.
Échange quadruple
Quadsort est basé sur un échange quadruple. Traditionnellement, la plupart des algorithmes de tri sont basés sur l'échange binaire, où deux variables sont triées à l'aide d'une troisième variable temporaire. Cela ressemble généralement à ceci:
if (val[0] > val[1])
{
tmp[0] = val[0];
val[0] = val[1];
val[1] = tmp[0];
}Dans un échange quadruple, le tri s'effectue à l'aide de quatre variables de substitution (swap). Dans la première étape, les quatre variables sont partiellement triées en quatre variables de swap, dans la deuxième étape, elles sont complètement triées dans les quatre variables d'origine.
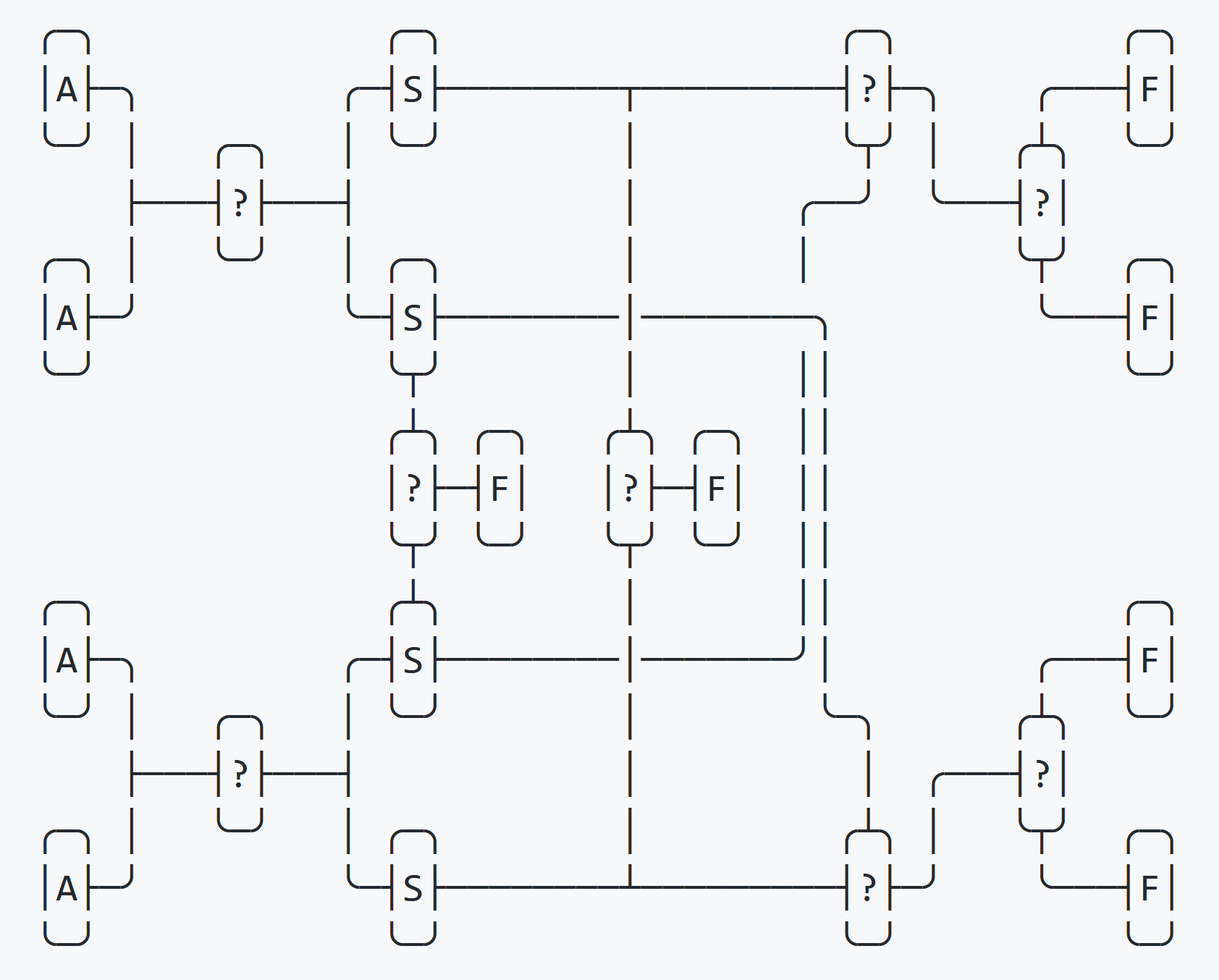
Ce processus est illustré dans le diagramme ci-dessus.
Après le premier tour de tri, un if check détermine si les quatre variables de swap sont triées dans l'ordre. Si tel est le cas, l'échange se termine immédiatement. Il vérifie ensuite si les variables de swap sont triées dans l'ordre inverse. Si tel est le cas, le tri se termine immédiatement. Si les deux tests échouent, l'emplacement final est connu et il reste deux tests pour déterminer l'ordre final.
Cela élimine une comparaison redondante pour les séquences qui sont dans l'ordre. En même temps, une comparaison supplémentaire est créée pour les séquences aléatoires. Cependant, dans le monde réel, nous comparons rarement des données vraiment aléatoires. Ainsi, lorsque les données sont ordonnées plutôt que désordonnées, ce changement de probabilité est bénéfique.
Il y a aussi une amélioration de la performance globale en éliminant le swap inutile. En C, un échange quadruple basique ressemble à ceci:
if (val[0] > val[1])
{
tmp[0] = val[1];
tmp[1] = val[0];
}
else
{
tmp[0] = val[0];
tmp[1] = val[1];
}
if (val[2] > val[3])
{
tmp[2] = val[3];
tmp[3] = val[2];
}
else
{
tmp[2] = val[2];
tmp[3] = val[3];
}
if (tmp[1] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[1];
val[2] = tmp[2];
val[3] = tmp[3];
}
else if (tmp[0] > tmp[3])
{
val[0] = tmp[2];
val[1] = tmp[3];
val[2] = tmp[0];
val[3] = tmp[1];
}
else
{
if (tmp[0] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[2];
}
else
{
val[0] = tmp[2];
val[1] = tmp[0];
}
if (tmp[1] <= tmp[3])
{
val[2] = tmp[1];
val[3] = tmp[3];
}
else
{
val[2] = tmp[3];
val[3] = tmp[1];
}
}Dans le cas où le tableau ne peut pas être parfaitement divisé en quatre parties, la queue de 1 à 3 éléments est triée en utilisant l'échange binaire traditionnel.
L'échange quadruple décrit ci-dessus est implémenté en quadsort.
Fusion quadruple
Lors de la première étape, l'échange quadruple pré-trie le tableau en blocs de quatre éléments, comme décrit ci-dessus.
La deuxième étape utilise une approche similaire pour détecter les ordres ordonnés et inversés, mais dans les blocs de 4, 16, 64 ou plus, cette étape est traitée comme un tri par fusion traditionnel.
Cela peut être représenté comme suit:
main memory: AAAA BBBB CCCC DDDD
swap memory: ABABABAB CDCDCDCD
main memory: ABCDABCDABCDABCDLa première ligne utilise un quadruple swap pour créer quatre blocs de quatre éléments triés chacun. La deuxième ligne utilise une fusion quadruple pour se combiner en deux blocs de huit éléments triés chacun dans la mémoire d'échange. Dans la dernière ligne, les blocs sont de nouveau fusionnés dans la mémoire principale, et il nous reste un bloc de 16 éléments triés. Voici la visualisation.

Ces opérations nécessitent en fait de doubler la mémoire d'échange. Plus à ce sujet plus tard.
Sauter
Une autre différence est qu'en raison du coût accru des opérations de fusion, il est avantageux de vérifier si quatre blocs sont dans l'ordre direct ou inverse.
Si les quatre blocs sont dans l'ordre, l'opération de fusion est ignorée car elle n'a aucun sens. Cependant, cela nécessite une vérification supplémentaire si, et pour les données triées aléatoirement, cette vérification devient de plus en plus improbable à mesure que la taille du bloc augmente. Heureusement, la fréquence de cette vérification est quadruplée à chaque cycle, tandis que l'avantage potentiel quadruple à chaque cycle.
Dans le cas où les quatre blocs sont dans l'ordre inverse, un échange sur place stable est effectué.
Dans le cas où seuls deux des quatre blocs sont ordonnés ou sont dans l'ordre inverse, les comparaisons dans la fusion elle-même sont inutiles et sont ensuite omises. Les données doivent encore être copiées pour permuter la mémoire, mais il s'agit d'une procédure moins informatique.
Cela permet à l'algorithme quadsort de trier les séquences dans l'ordre avant et arrière en utilisant des
ncomparaisons au lieu de n * log ncomparaisons.
Contrôles des limites
Un autre problème avec le tri par fusion traditionnel est qu'il gaspille des ressources en vérifications de limites inutiles. Cela ressemble à ceci:
while (a <= a_max && b <= b_max)
if (a <= b)
[insert a++]
else
[insert b++]Pour l'optimisation, notre algorithme compare le dernier élément de la séquence A avec le dernier élément de la séquence B.Si le dernier élément de la séquence A est inférieur au dernier élément de la séquence B, alors nous savons que le test
b < b_maxsera toujours faux, car la séquence A est la première à fusionner complètement.
De même, si le dernier élément de la séquence A est supérieur au dernier élément de la séquence B, on sait que le test
a < a_maxsera toujours faux. Cela ressemble à ceci:
if (val[a_max] <= val[b_max])
while (a <= a_max)
{
while (a > b)
[insert b++]
[insert a++]
}
else
while (b <= b_max)
{
while (a <= b)
[insert a++]
[insert b++]
}Fusion queue
Lorsque vous triez un tableau de 65 éléments, vous vous retrouvez avec un tableau trié à 64 éléments et un tableau trié à un élément à la fin. Cela ne résultera pas en une opération supplémentaire de swap (échange) si toute la séquence est en ordre. Dans tous les cas, pour cela, le programme doit choisir la taille optimale du tableau (64, 256 ou 1024).
Un autre problème est que la taille non optimale du tableau conduit à des opérations d'échange inutiles. Pour contourner ces deux problèmes, la procédure de fusion quadruple est abandonnée lorsque la taille de bloc atteint 1/8 de la taille du tableau et le reste du tableau est trié à l'aide de la fusion de queue. Le principal avantage de la fusion de la queue est qu'elle permet de réduire le swap du quadort à n / 2 sans impact significatif sur les performances.
Grand O
| Nom | Meilleur | Milieu | Pire | Stable | Mémoire |
|---|---|---|---|---|---|
| quad | n | n log n | n log n | Oui | n |
Lorsque les données sont déjà triées ou triées dans l'ordre inverse, quadsort effectue n comparaisons.
Cache
Puisque quadsort utilise n / 2 swaps, l'utilisation du cache n'est pas aussi idéale que le tri sur place. Cependant, le tri des données aléatoires en place entraîne des échanges sous-optimaux. Sur la base de mes points de repère, le tri quadripolaire est toujours plus rapide que le tri sur place, tant que le tableau ne déborde pas du cache L1, qui peut atteindre 64 Ko sur les processeurs modernes.
Wolfsort
Wolfsort est un algorithme de tri hybride radixsort / quadsort qui améliore les performances lorsque vous travaillez avec des données aléatoires. Il s'agit essentiellement d'une preuve de concept qui ne fonctionne qu'avec des entiers 32 et 64 bits non signés.
Visualisation
La visualisation ci-dessous exécute quatre tests. Le premier test est basé sur une distribution aléatoire, le second sur une distribution ascendante, le troisième sur une distribution descendante et le quatrième sur une distribution ascendante avec une queue aléatoire.
La moitié supérieure montre le swap et la moitié inférieure montre la mémoire principale. Les couleurs varient pour les opérations de saut, d'échange, de fusion et de copie.
Benchmark: quadsort, std :: stable_sort, timsort, pdqsort et wolfsort
Le test de performance suivant a été exécuté sur la configuration de WSL gcc version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). Le code source est compilé par l'équipe
g++ -O3 quadsort.cpp. Chaque test est exécuté une centaine de fois et seule la meilleure exécution est signalée.
L'abscisse est le temps d'exécution.
Fiche technique Quadsort, std :: stable_sort, timsort, pdqsort et wolfsort
| quadsort | 1000000 | i32 | 0.070469 | 0.070635 | ||
| stablesort | 1000000 | i32 | 0.073865 | 0.074078 | ||
| timsort | 1000000 | i32 | 0.089192 | 0.089301 | ||
| pdqsort | 1000000 | i32 | 0.029911 | 0.029948 | ||
| wolfsort | 1000000 | i32 | 0.017359 | 0.017744 | ||
| quadsort | 1000000 | i32 | 0.000485 | 0.000511 | ||
| stablesort | 1000000 | i32 | 0.010188 | 0.010261 | ||
| timsort | 1000000 | i32 | 0.000331 | 0.000342 | ||
| pdqsort | 1000000 | i32 | 0.000863 | 0.000875 | ||
| wolfsort | 1000000 | i32 | 0.000539 | 0.000579 | ||
| quadsort | 1000000 | i32 | 0.008901 | 0.008934 | () | |
| stablesort | 1000000 | i32 | 0.017093 | 0.017275 | () | |
| timsort | 1000000 | i32 | 0.008615 | 0.008674 | () | |
| pdqsort | 1000000 | i32 | 0.047785 | 0.047921 | () | |
| wolfsort | 1000000 | i32 | 0.012490 | 0.012554 | () | |
| quadsort | 1000000 | i32 | 0.038260 | 0.038343 | ||
| stablesort | 1000000 | i32 | 0.042292 | 0.042388 | ||
| timsort | 1000000 | i32 | 0.055855 | 0.055967 | ||
| pdqsort | 1000000 | i32 | 0.008093 | 0.008168 | ||
| wolfsort | 1000000 | i32 | 0.038320 | 0.038417 | ||
| quadsort | 1000000 | i32 | 0.000559 | 0.000576 | ||
| stablesort | 1000000 | i32 | 0.010343 | 0.010438 | ||
| timsort | 1000000 | i32 | 0.000891 | 0.000900 | ||
| pdqsort | 1000000 | i32 | 0.001882 | 0.001897 | ||
| wolfsort | 1000000 | i32 | 0.000604 | 0.000625 | ||
| quadsort | 1000000 | i32 | 0.006174 | 0.006245 | ||
| stablesort | 1000000 | i32 | 0.014679 | 0.014767 | ||
| timsort | 1000000 | i32 | 0.006419 | 0.006468 | ||
| pdqsort | 1000000 | i32 | 0.016603 | 0.016629 | ||
| wolfsort | 1000000 | i32 | 0.006264 | 0.006329 | ||
| quadsort | 1000000 | i32 | 0.018675 | 0.018729 | ||
| stablesort | 1000000 | i32 | 0.026384 | 0.026508 | ||
| timsort | 1000000 | i32 | 0.023226 | 0.023395 | ||
| pdqsort | 1000000 | i32 | 0.028599 | 0.028674 | ||
| wolfsort | 1000000 | i32 | 0.009517 | 0.009631 | ||
| quadsort | 1000000 | i32 | 0.037593 | 0.037679 | ||
| stablesort | 1000000 | i32 | 0.043755 | 0.043899 | ||
| timsort | 1000000 | i32 | 0.047008 | 0.047112 | ||
| pdqsort | 1000000 | i32 | 0.029800 | 0.029847 | ||
| wolfsort | 1000000 | i32 | 0.013238 | 0.013355 | ||
| quadsort | 1000000 | i32 | 0.009605 | 0.009673 | ||
| stablesort | 1000000 | i32 | 0.013667 | 0.013785 | ||
| timsort | 1000000 | i32 | 0.007994 | 0.008138 | ||
| pdqsort | 1000000 | i32 | 0.024683 | 0.024727 | ||
| wolfsort | 1000000 | i32 | 0.009642 | 0.009709 |
Il convient de noter que pdqsort n'est pas un tri stable, il fonctionne donc plus rapidement avec des données dans l'ordre normal (ordre général).
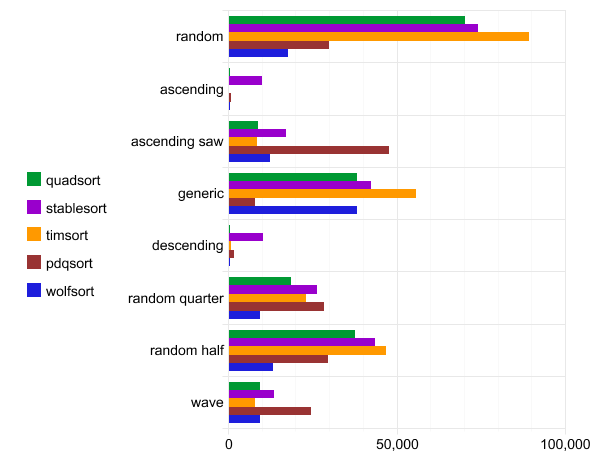
Le benchmark suivant a été exécuté sur WSL gcc version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). Le code source est compilé par l'équipe
g++ -O3 quadsort.cpp. Chaque test est exécuté une centaine de fois et seule la meilleure exécution est signalée. Il mesure les performances sur des baies allant de 675 à 100 000 éléments.
L'axe X du graphique ci-dessous est la cardinalité, l'axe Y est le temps d'exécution.

Fiche technique Quadsort, std :: stable_sort, timsort, pdqsort et wolfsort
| quadsort | 100000 | i32 | 0.005800 | 0.005835 | ||
| stablesort | 100000 | i32 | 0.006092 | 0.006122 | ||
| timsort | 100000 | i32 | 0.007605 | 0.007656 | ||
| pdqsort | 100000 | i32 | 0.002648 | 0.002670 | ||
| wolfsort | 100000 | i32 | 0.001148 | 0.001168 | ||
| quadsort | 10000 | i32 | 0.004568 | 0.004593 | ||
| stablesort | 10000 | i32 | 0.004813 | 0.004923 | ||
| timsort | 10000 | i32 | 0.006326 | 0.006376 | ||
| pdqsort | 10000 | i32 | 0.002345 | 0.002373 | ||
| wolfsort | 10000 | i32 | 0.001256 | 0.001274 | ||
| quadsort | 5000 | i32 | 0.004076 | 0.004086 | ||
| stablesort | 5000 | i32 | 0.004394 | 0.004420 | ||
| timsort | 5000 | i32 | 0.005901 | 0.005938 | ||
| pdqsort | 5000 | i32 | 0.002093 | 0.002107 | ||
| wolfsort | 5000 | i32 | 0.000968 | 0.001086 | ||
| quadsort | 2500 | i32 | 0.003196 | 0.003303 | ||
| stablesort | 2500 | i32 | 0.003801 | 0.003942 | ||
| timsort | 2500 | i32 | 0.005296 | 0.005322 | ||
| pdqsort | 2500 | i32 | 0.001606 | 0.001661 | ||
| wolfsort | 2500 | i32 | 0.000509 | 0.000520 | ||
| quadsort | 1250 | i32 | 0.001767 | 0.001823 | ||
| stablesort | 1250 | i32 | 0.002812 | 0.002887 | ||
| timsort | 1250 | i32 | 0.003789 | 0.003865 | ||
| pdqsort | 1250 | i32 | 0.001036 | 0.001325 | ||
| wolfsort | 1250 | i32 | 0.000534 | 0.000655 | ||
| quadsort | 675 | i32 | 0.000368 | 0.000592 | ||
| stablesort | 675 | i32 | 0.000974 | 0.001160 | ||
| timsort | 675 | i32 | 0.000896 | 0.000948 | ||
| pdqsort | 675 | i32 | 0.000489 | 0.000531 | ||
| wolfsort | 675 | i32 | 0.000283 | 0.000308 |
Benchmark: quadsort et qsort (mergesort)
Le benchmark suivant a été exécuté sur WSL gcc version 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). Le code source est compilé par l'équipe
g++ -O3 quadsort.cpp. Chaque test est exécuté une centaine de fois et seule la meilleure exécution est signalée.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)MO indique le nombre de comparaisons effectuées sur 1 million d'éléments.
Le benchmark ci-dessus compare quadsort à glibc qsort () via la même interface à usage général et sans aucun avantage injuste connu tel que l'inlining.
random order: 635, 202, 47, 229, etc
ascending order: 1, 2, 3, 4, etc
uniform order: 1, 1, 1, 1, etc
descending order: 999, 998, 997, 996, etc
wave order: 100, 1, 102, 2, 103, 3, etc
stable/unstable: 100, 1, 102, 1, 103, 1, etc
random range: time to sort 1000 arrays ranging from size 0 to 999 containing random dataBenchmark: quadsort et qsort (tri rapide)
Ce test particulier est fait en utilisant l'implémentation qsort () de Cygwin, qui utilise quicksort sous le capot. Le code source est compilé par l'équipe
gcc -O3 quadsort.c. Chaque test est exécuté cent fois, seule la meilleure exécution est signalée.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)Dans ce benchmark, il devient clair pourquoi le tri rapide est souvent préférable à la fusion traditionnelle, il fait moins de comparaisons pour les données dans l'ordre croissant, uniformément distribuées, et pour les données dans l'ordre décroissant. Cependant, dans la plupart des tests, ses performances sont moins bonnes que celles du quadort. Quicksort présente également une vitesse de tri extrêmement lente pour les données ordonnées par vague. Le test de données aléatoires montre que le quadruple tri est deux fois plus rapide lors du tri de petits tableaux.
Quicksort est plus rapide dans les tests généraux et stables, mais uniquement parce qu'il s'agit d'un algorithme instable.
Voir également: