IBM a publié le code source de la boîte à outils FHE pour Linux sur GitHub . Les utilitaires fonctionnent sur les plates-formes IBM Z et x86 et sont pris en charge par Ubuntu, Fedora et CentOS.
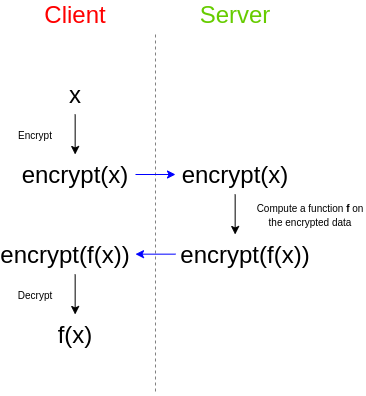
Le cryptage entièrement homomorphe (FHE) a longtemps été considéré comme une partie du Saint Graal en cryptographie. La tâche semblait vraiment irréaliste. Le type de cryptage FHE suppose la manipulation de données cryptées par un tiers sans possibilité de décrypter les données elles-mêmes ou le résultat de la manipulation.
Comment est-ce possible?
À titre d'exemple simple, imaginez que vous avez un tas d'e-mails et que vous souhaitez utiliser un filtre anti-spam tiers pour vérifier s'il s'agit de spam. Le filtre anti-spam fonctionne sur le serveur car le développeur essaie de garder son algorithme confidentiel: soit il cache le code source, soit le filtre anti-spam dépend d'une très grande base de données qu'il ne souhaite pas divulguer publiquement, car cela facilite l'attaque, ou les deux autre. Peu importe, l'essentiel est que le filtre anti-spam fonctionne de toute façon sur le serveur - et vous ne pouvez pas l'exécuter seul. Que faire dans une telle situation? Vous vous souciez également de la confidentialité de vos données et ne souhaitez pas transférer le contenu des e-mails à des tiers sous une forme ouverte et non cryptée. C'est là que le cryptage totalement homomorphe vient à la rescousse:
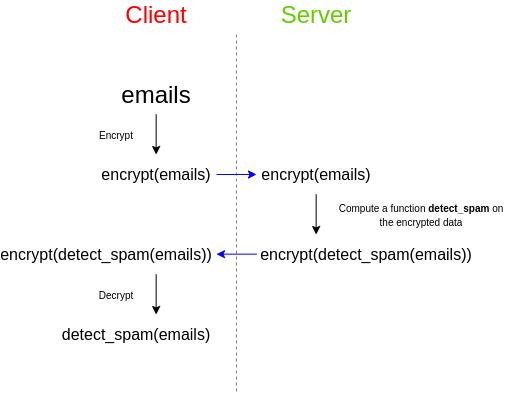
Ainsi, le service garde l'algorithme secret et vous gardez vos données secrètes. Mais FHE permet d'appliquer avec succès l'algorithme sur ces données, de sorte qu'aucun côté n'apprenne les secrets de l'autre.
Le cryptage totalement homomorphe a de nombreuses utilisations, y compris dans la blockchain, où le serveur peut manipuler les données client cryptées sans divulguer le contenu des informations. Autrement dit, le serveur peut répondre aux demandes du client sans savoir ce qu'il a demandé .
Autres utilisations du cryptage homomorphe:
- Des protocoles d' adresses cachées plus efficaces et des solutions d'évolutivité plus générales pour les protocoles de confidentialité qui exigent aujourd'hui que chaque utilisateur scanne personnellement l'ensemble de la blockchain pour les transactions entrantes.
- , , .
- , ( , , , ).
En général, il existe différents types de cryptage homomorphique, certains plus puissants que d'autres. Ils diffèrent dans les opérations pouvant être effectuées avec des données cryptées.
Le chiffrement partiellement homomorphe vous permet de ne faire qu'une seule opération avec des données chiffrées, soit l'addition ou la multiplication, le chiffrement
partiellement homomorphique (quelque peu homomorphe) ne fonctionne entièrement que sur un ensemble de données limité.
Enfin, le cryptage entièrement homomorphe permet des opérations d'addition et de multiplication illimitées sur n'importe quel ensemble de données.
La mise en œuvre d'un chiffrement homomorphique partiel est assez simple: par exemple, la multiplication est implémentée en RSA:
, , pour que
Les courbes elliptiques offrent une option de pliage similaire. Mais mettre en œuvre à la fois l' addition et la multiplication est beaucoup plus difficile. La recherche d'un tel schéma se poursuit depuis 1978, lorsque Rivest, Adleman et Dertuzos ont formulé le problème et inventé le terme de «cryptage homomorphe». Depuis 30 ans, l'existence de systèmes totalement homomorphes n'a pas été prouvée, et Rivest lui-même a décidé que l'idée n'était pas sujette à mise en œuvre.
Une percée majeure n'a eu lieu qu'en 2009 après la publication de la thèse de doctorat de l'étudiant diplômé de Stanford Craig Gentry. Il a décrit une possible construction d'un cryptosystème complètement homomorphe sur des réseaux idéaux . Dans sa thèse, il a également proposé une idée innovante de bootstrap .... Cette astuce transforme le schéma FHE partiel en un schéma de cryptage entièrement homomorphe. La méthode d'amorçage est illustrée dans le diagramme ci-dessous. En bref, ici les bits de la clé secrète sont cryptés avec la clé publique dans un schéma homomorphe et publiés comme une "clé de rappel", ce qui permet d'effectuer un cryptage homomorphique sur le texte chiffré rechiffré, dans lequel le bruit est réduit à la taille d'origine. Autrement dit, nous "actualisons" le texte chiffré, comme pour effacer l'erreur de l'ancienne clé.
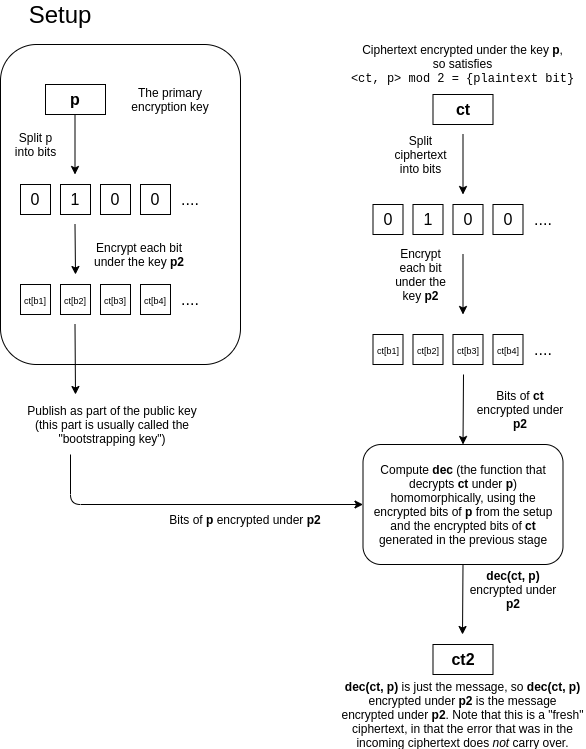
En termes simples, la procédure de décryptage elle-même est un calcul, elle peut donc être implémentée sous la forme d'un schéma homomorphe qui accepte les bits de texte chiffré et les bits d'une clé secrète en entrée.
Le schéma cryptographique de Gentry était une percée majeure, mais a introduit une nouvelle erreur indépendante de la quantité d'erreur dans le cryptage d'origine. L'auteur lui-même a décrit une solution complexe au problème, mais le schéma Brackersky et Vaikuntanathan modifié proposé en 2011 (le schéma s'appelait BGV (Brackersky-Gentry-Vaikuntanatan)) a connu plus de succès . En 2013, IBM a publié une bibliothèque cryptographique gratuite HELib avec prise en charge du cryptage homomorphe et des schémas BGV En janvier 2020, la version 1.0.0 d'HELib est sortie .
En 2013, Gentry s'est de nouveau déclaré. Avec les co-auteurs Sahai et Waters et a présenté un schéma de cryptage homomorphique complet de troisième génération - le schéma GSW (Gentry, Sahai, Waters), qui utilise à nouveau la cryptographie en treillis et le boostrapping.
Au fil des années de développement, un ensemble complet d'outils avec des échantillons intégrés pour les IDE a été créé sur la base d'HELib, qui fonctionne hors de la boîte.
IBM a précédemment publié des outils de chiffrement entièrement homomorphes pour macOS et iOS . À l'avenir, il promet de publier le code source de la version pour Android.
La version Linux a été publiée plutôt à des fins de démonstration et fonctionne sur une base de données avec les pays européens et leurs capitales (le deuxième exemple pour le secteur financier est la reconnaissance de fraude par un réseau neuronal basé sur une base cryptée de transactions anonymes). Jusqu'à présent, il n'est pas arrivé à l'application pratique du cryptage homomorphe. Selon leGentry lui-même en 2009, par exemple, traiter une requête de recherche dans Google au cas où le texte serait chiffré nécessiterait environ mille milliards de fois plus de calculs. Néanmoins, les optimisations apportées par IBM ont considérablement amélioré les performances de la bibliothèque, de sorte que dans quelques années ou décennies, elle pourrait bien être largement utilisée dans les applications Web. IBM indique que la bibliothèque peut désormais fonctionner sur les mainframes IBM Z.