L'impédance caractéristique d'une ligne sans perte est exprimée par la formule bien connue:
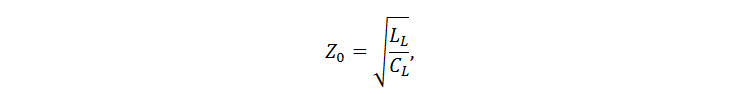
où L L et C L sont l'inductance linéaire et la capacité de ligne (c'est-à-dire par unité de longueur). Je pense qu'il sera utile de préciser d'où il vient. Considérons une section extrêmement petite d'une longue ligne de transmission à deux fils, à travers laquelle un courant alternatif circule (Fig. 1). Le courant est alternatif, donc les valeurs instantanées du courant, de la tension entre les fils, de la densité linéaire de la charge électrique changent le long des fils.
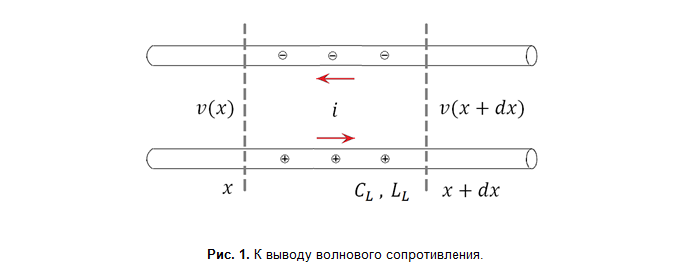
La loi de conservation de la charge pour le tronçon de câble et la loi de Faraday pour le circuit sont les suivantes:

Pour une droite sans pertes (R L = 0) et en tenant compte de Φ L = L L ∙ i et q L = C L ∙ v on obtient:
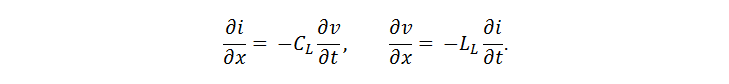
Ces équations différentielles sont réduites à une forme d'onde, pour laquelle on obtient:
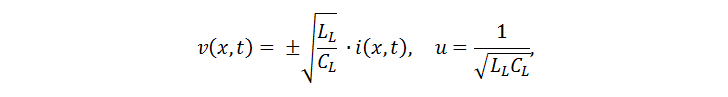
où u est la vitesse de propagation des ondes, et le coefficient reliant le courant dans les fils et la tension entre les fils est l'impédance caractéristique. Voici quelques relations utiles (TD - délai de ligne):
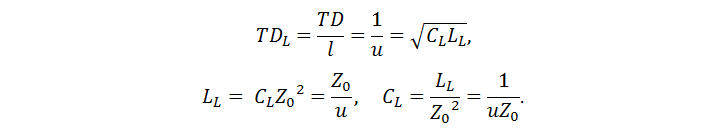
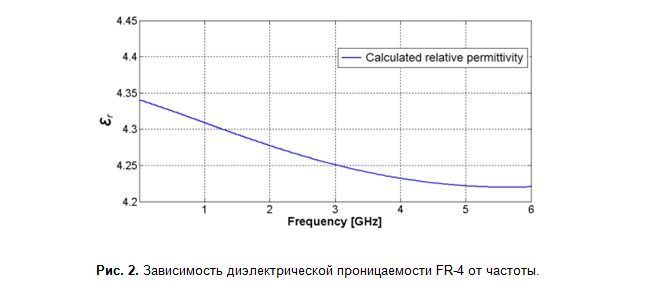
La capacité et l'inductance dépendent de la fréquence, par conséquent l'impédance caractéristique change avec la fréquence. L'influence de l'effet peau sur l'inductance est limitée à des fréquences allant jusqu'à plusieurs dizaines de mégahertz, dans la plage de fréquences supérieure elle change de manière insignifiante. La valeur de la capacité est affectée par la dépendance de la constante diélectrique du matériau PCB sur la fréquence, et pour les lignes microruban, en raison de l'asymétrie du diélectrique, également de l'effet de la dispersion. Les données pour la fibre de verre FR-4 dans différentes sources diffèrent, cependant, à titre d'estimation, on peut supposer que la constante diélectrique diminue de 0,15-0,2 chaque décennie (figure 2). La différence de données est due au fait que FR-4 est une classe de matériaux. Il se compose de fibre de verre et de résine époxy avec des constantes diélectriques sensiblement différentes (Fig. 3).Plus il y a de résine dans le matériau, moins est la valeur moyenne en volume de la constante diélectrique du stratifié de fibres de verre. Par conséquent, des valeurs différentes pour différents fabricants. À propos, en raison d'une telle anisotropie, la constante diélectrique dépend également de la direction - longitudinale ou transversale, ce qui affecte les calculs pour les lignes différentielles, car la configuration du champ différera en fonction du mode.

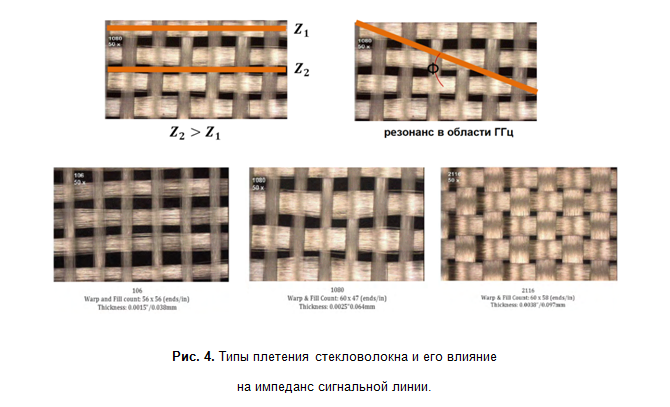
L'agencement mutuel de la fibre de verre et des fibres conductrices affecte également l'impédance caractéristique. Si le conducteur est situé au-dessus de la fibre, alors son impédance caractéristique sera légèrement plus élevée par rapport au conducteur adjacent, qui est tombé dans l'espace entre les fibres. Si le conducteur est dirigé à un angle par rapport aux fibres, cela conduit à un changement périodique de l'impédance caractéristique et des effets de résonance à des fréquences voisines de la dizaine de GHz. Le degré d'influence dépend fortement du type de tissage en fibre de verre (Fig. 4). C'est pourquoi il existe des matériaux spécialisés pour les circuits imprimés haute fréquence, où l'influence de ces effets devient significative. Les paramètres de tels diélectriques ont une meilleure stabilité sur une large gamme de fréquences et sont bien mieux documentés.
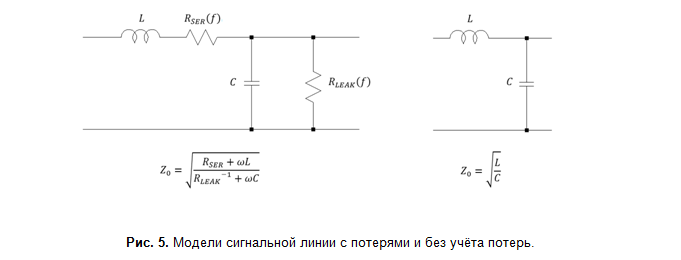
En ce qui concerne les pertes (Fig. 5), pour la plupart des cas pratiques, le modèle à faibles pertes est applicable, pour lequel les pertes aux hautes fréquences peuvent être négligées R SER ≪ ωL, R LEAK ≫1⁄ωC. Cette simplification a permis de développer des modèles efficaces qui permettent un calcul très précis des paramètres de ligne de signal à l'aide de fonctions standard.
Les lignes de signaux planaires ont été inventées au début des années 1950, et des modèles mathématiques précis ont été développés presque immédiatement pour les lignes de bande, et il a fallu plusieurs décennies pour créer un modèle d'analyse microruban précis. Harold Wheeler fut l' un des premiers (en 1965) à donner des solutions exactes à des cas particuliers , qu'il généralisa plus tard (en 1977) . La raison est l'asymétrie du diélectrique, qui conduit à une distribution complexe du champ électrique, qui dépend également de la fréquence.
Naturellement, ce modèle n'était pas le seul - et en 1988, il y en avait suffisamment pour le rendre intéressant à comparer. C'est faitle grand et terrible Eric Bogatin. Je suis tombé sur cet article en choisissant un modèle de calcul pour une calculatrice. Ensuite, je suis arrivé aux publications de Wheeler, où il y a beaucoup de pages de mathématiques cool avec des transformations conformes, et j'ai réalisé que Bogatin ne l'avait pas lu attentivement (ou ne l'avait pas lu du tout) et grossier son modèle, ce qui a influencé les résultats de la comparaison. Ensuite, cette erreur a migré vers la 2007e année. Dans le même temps, Bogatin lui-même se réfère à la monographie «Microwave Transmission Line Impedance Data» d' un certain M.A.R. Gunstan, mais je n'ai plus commencé à creuser là où poussent les jambes, reconnaissant le camarade Bogatin comme le coupable (que, d'ailleurs, je respecte beaucoup, Bogatin est la force).
Alors quel est le point. Bogatin a mesuré expérimentalement la capacité linéaire de lignes microruban de différentes largeurs (à une fréquence de 1 kHz) et les a comparées aux valeurs calculées (Fig. 6).
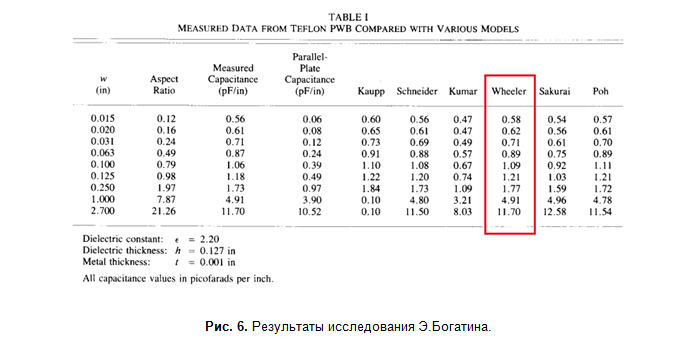
Dans tous les modèles dont j'ai étudié les sources primaires, des relations analytiques pour l'impédance d'onde sont données. La capacité est calculée en utilisant le ratio suivant:
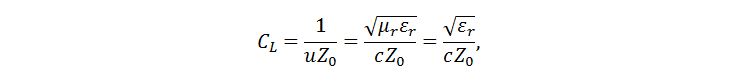
où ε r est la constante diélectrique, c est la vitesse de la lumière. L'asymétrie du diélectrique conduit au fait qu'il faut inventer la valeur efficace de la constante diélectrique. Bogatin écrit:
Dans le cas de Wheeler [13], aucun modèle de constante diélectrique effective n'est proposé. Cependant, sur la base de la suggestion de Gunsten [6], le tracé du modèle de Wheeler utilise la constante diélectrique effective du modèle de Schneider.
et utilise un modèle hybride Wheeler-Schneider (résultat en pF / pouce):
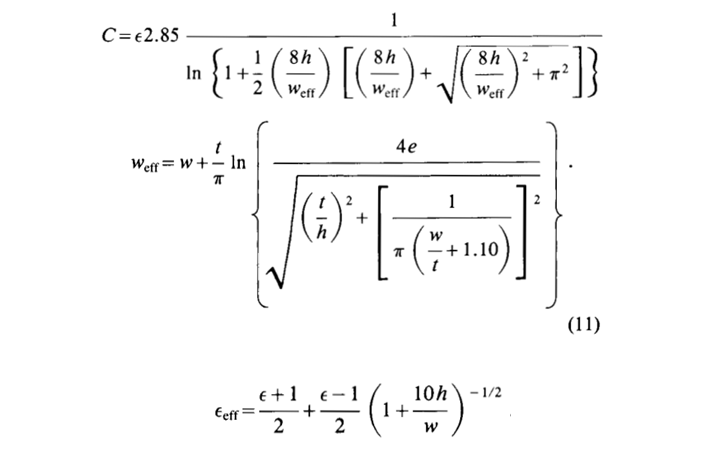
Selon les résultats de l'expérience, le modèle donne une bonne précision et Bogatin fait l'éloge de son vélo inventé:
La combinaison du modèle de Wheeler et de Schneider est en accord avec les données publiées précédemment et les nouvelles données présentées ici à mieux que 3 pour cent, et est d'une forme appropriée pour une utilisation dans une feuille de calcul. En plus d'être utile pour la simulation informatique de conceptions spécifiques, ce modèle peut fournir des informations utiles à ajouter à l'intuition des ingénieurs de fabrication et de conception.
Passons maintenant à la source d'origine. Les formules utilisées par Bogatin sont des formules simplifiées pour le cas sans diélectrique:
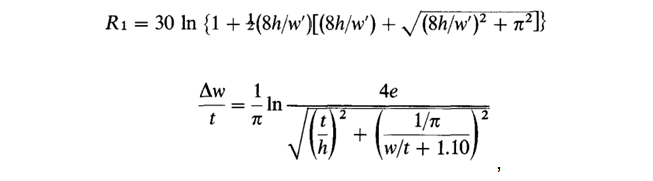
et le modèle complet ressemble à ceci:
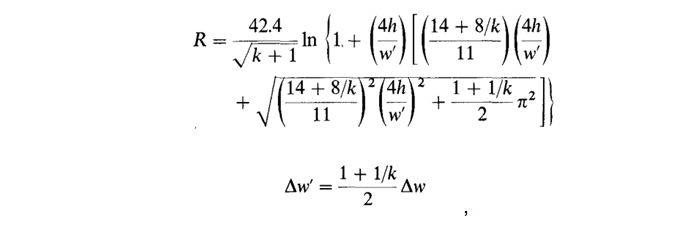
ici, dans la notation de Wheeler, R est la résistance d'onde, k est la constante diélectrique, R 1 = R (k = 1) est la résistance sans diélectrique, ∆w est la correction de largeur tenant compte de l'épaisseur du conducteur, ∆w 'est la correction tenant compte de l'influence du diélectrique. Wheeler utilise la notation k 'pour la constante diélectrique effective et lui donne la formule suivante:
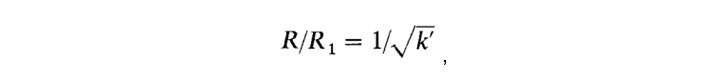
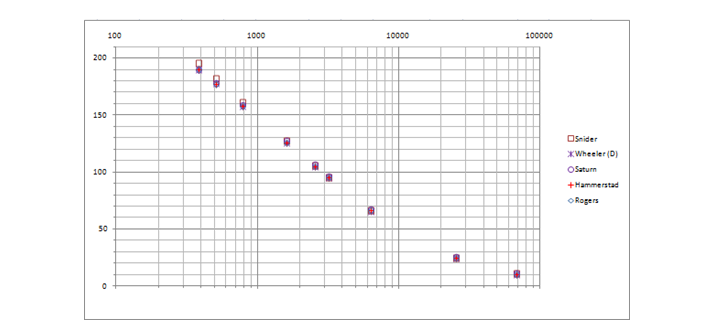
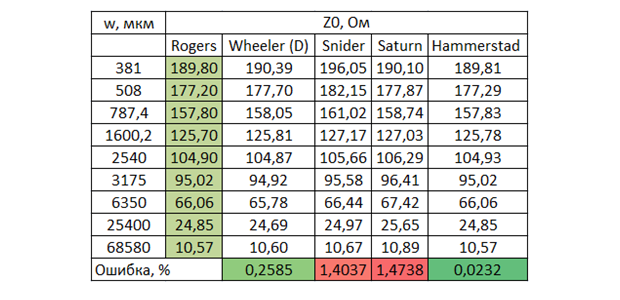
ce qui n'est pas aussi simple, bien sûr, que celui de Schneider, mais c'est néanmoins dans le modèle. J'ai répété les calculs de Bogatin, laissant les modèles les plus précis: Schneider, Wheeler, leur version hybride - et ajouté les résultats du calcul à l'aide du calculateur Saturn PCB Toolkit et du modèle Hammerstead . Pour plus de clarté, je présente à la fois un graphique et des données tabulaires avec une erreur relative aux données expérimentales.
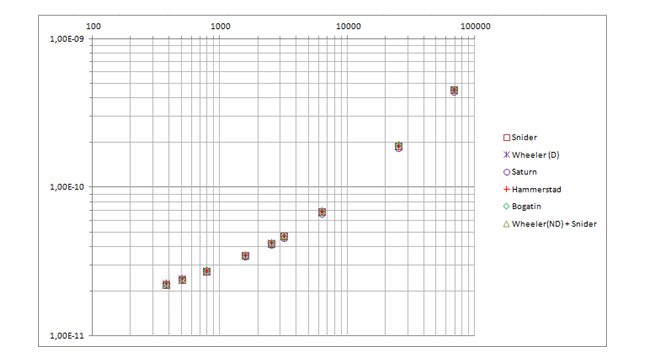
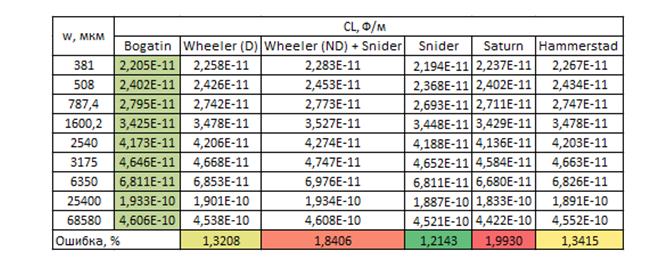
Compte tenu des erreurs de mesure et de la constante diélectrique du matériau de base (2,2 ± 1%), on peut dire que tous les modèles sont bien corrélés aux données expérimentales, ce n'est pas en vain que les chercheurs ont ajusté les formules pendant des années. Je m'attendais à plus de précision de Saturne, car il dit directement qu'il utilise une formule "pas simple, mais complexe" et que la précision est comparable à Sonnet 3D. De plus, là, l'épaisseur ne peut être sélectionnée qu'en onces, soit ½ oz. (18 microns), ou 1 oz. (35 μm) et 1 mil (25,4 μm) n'est pas spécifié. Les valeurs du tableau sont pour ½ oz., Puisqu'elles sont plus proches des données expérimentales obtenues de cette façon. Il est également évident que le modèle original de Wheeler aurait été plus précis sur cet échantillon de données, donc j'étais agacé par lui. Surtout considérant queque le même modèle de Schneider présente un sérieux inconvénient - il ne prend pas en compte l'effet de l'épaisseur du conducteur, qui n'a presque aucun effet sur la capacité, mais est significatif pour l'inductance et donc la résistance d'onde elle-même. Malheureusement, Bogatin ne donne pas la valeur de l'impédance d'onde, il a donc utilisécalculatrice de la société réputée Rogers. Le Saturne cette fois est de 1 once. il a donné une précision un peu meilleure, la logique de son travail ne m'est pas encore très claire. Le graphique montre qu'à mesure que la largeur diminue (là où l'effet de l'épaisseur augmente), Schneider tombe. Et Rogers, apparemment, est basé sur le modèle Hammerstead. Au départ , je l'ai fait sur Wheeler , mais étant donné que la plupart des calculatrices avancées sont sur Hammerstead, il sera possible de passer à ce modèle afin de les suivre (bien que le modèle ne dispose pas d' une formule explicite pour la synthèse, contrairement à Wheeler).
En fait, je considère que la justice est rétablie sur ce point. Wheeler est le pouvoir. Même Bogatin a parfois tort. Alors ne faites pas confiance, vérifiez et revérifiez. Utilisez les calculs pour vos lignes de signal. Au fait. Veuillez partager dans les commentaires si vous utilisez le calcul de la résistance des vagues et si oui, avec quelle aide?
PS Je suis en train de travailler sur la calculatrice et je suis en train de finaliser le livre , maintenant mes mains ont atteint la version gratuite - j'ai ajouté toutes les améliorations et correctifs qui n'étaient que complètement introduits auparavant. Bonne chance à tous!