
Source: Vecteezy
Oui, la régression linéaire n'est pas la seule. Nommez
rapidement cinq algorithmes d'apprentissage automatique.
Il est peu probable que vous nommiez de nombreux algorithmes de régression. Après tout, le seul algorithme de régression largement utilisé est la régression linéaire, principalement en raison de sa simplicité. Cependant, la régression linéaire est souvent inapplicable aux données réelles en raison d'options trop limitées et d'une liberté de manœuvre limitée. Il est souvent utilisé uniquement comme modèle de base pour l'évaluation et la comparaison avec de nouvelles approches de recherche.
Équipe Mail.ru Cloud Solutionstraduit un article dont l'auteur décrit 5 algorithmes de régression. Ils valent la peine de les avoir dans votre boîte à outils, ainsi que des algorithmes de classification populaires tels que SVM, arbre de décision et réseaux de neurones.
1. Régression du réseau neuronal
Théorie
Les réseaux de neurones sont incroyablement puissants, mais ils sont couramment utilisés pour la classification. Les signaux voyagent à travers des couches de neurones et sont résumés dans l'une de plusieurs classes. Cependant, ils peuvent être très rapidement adaptés en modèles de régression en modifiant la dernière fonction d'activation.
Chaque neurone transmet les valeurs de la connexion précédente via une fonction d'activation servant à la généralisation et à la non-linéarité. Habituellement, la fonction d'activation est quelque chose comme une fonction sigmoïde ou ReLU (unité linéaire rectifiée).
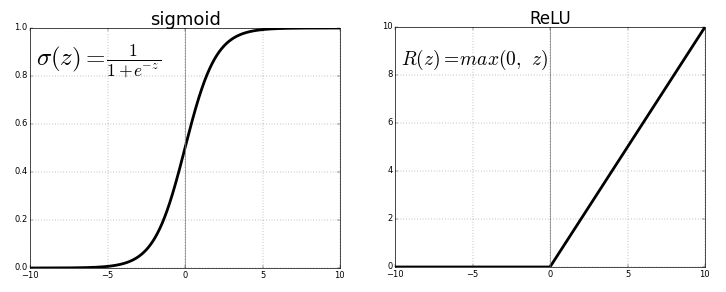
Source . Image libre
Mais, en remplaçant la dernière fonction d'activation (neurone de sortie) par une fonction linéairela fonction d'activation, le signal de sortie peut être mappé à de nombreuses valeurs en dehors des classes fixes. Ainsi, la sortie ne sera pas la probabilité d'affecter le signal d'entrée à une classe quelconque, mais une valeur continue à laquelle le réseau neuronal fixe ses observations. En ce sens, on peut dire que le réseau de neurones complète la régression linéaire.
La régression du réseau neuronal présente l'avantage de la non-linéarité (en plus de la complexité) qui peut être introduite avec les fonctions d'activation sigmoïde et non linéaire plus tôt dans le réseau neuronal. Cependant, la surutilisation de ReLU en tant que fonction d'activation peut signifier que le modèle a tendance à éviter de produire des valeurs négatives, puisque ReLU ignore les différences relatives entre les valeurs négatives.
Cela peut être résolu soit en limitant l'utilisation de ReLU et en ajoutant plus de valeurs négatives des fonctions d'activation correspondantes, soit en normalisant les données dans une plage strictement positive avant l'entraînement.
la mise en oeuvre
En utilisant Keras, construisons une structure de réseau neuronal artificiel, bien que la même chose puisse être faite avec un réseau neuronal convolutif ou un autre réseau si la dernière couche est soit une couche dense avec activation linéaire, soit juste une couche avec activation linéaire. ( Notez que les importations Keras ne sont pas répertoriées pour économiser de l'espace ).
model = Sequential()
model.add(Dense(100, input_dim=3, activation='sigmoid'))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation='sigmoid'))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation='softmax'))
#IMPORTANT PART
model.add(Dense(1, activation='linear'))
Le problème avec les réseaux de neurones a toujours été leur forte variance et leur tendance au surajustement. Il existe de nombreuses sources de non-linéarité dans l'exemple de code ci-dessus, comme SoftMax ou sigmoid.
Si votre réseau de neurones fait du bon travail avec des données d'entraînement avec une structure purement linéaire, il peut être préférable d'utiliser une régression par arbre de décision tronqué, qui émule un réseau de neurones linéaire et hautement dispersé, mais permet au scientifique des données d'avoir un meilleur contrôle sur la profondeur, la largeur et d'autres attributs pour contrôler le surajustement.
2. Régression de l'arbre de décision
Théorie
Les arbres de décision dans la classification et la régression sont très similaires en ce sens qu'ils fonctionnent en construisant des arbres avec des nœuds oui / non. Cependant, alors que les nœuds feuilles de classification donnent une valeur de classe unique (par exemple, 1 ou 0 pour un problème de classification binaire), les arbres de régression se retrouvent avec une valeur en mode continu (par exemple, 4593,49 ou 10,98).
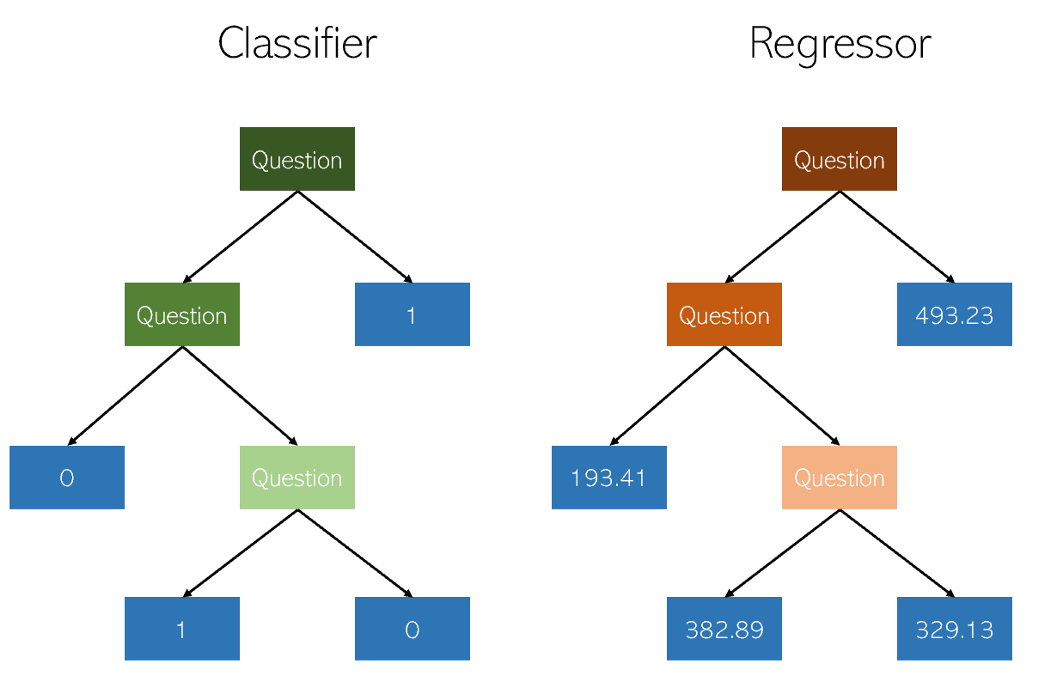
Illustration de l'auteur
En raison de la nature spécifique et très dispersée de la régression en tant que simple problème d'apprentissage automatique, les régresseurs d'arbre de décision doivent être soigneusement élagués. Cependant, l'approche de régression est irrégulière - au lieu de calculer la valeur sur une échelle continue, elle arrive à des nœuds d'extrémité donnés. Si le régresseur est trop coupé, il a trop peu de nœuds feuilles pour remplir correctement son objectif.
Par conséquent, l'arbre de décision doit être élagué afin qu'il ait le plus de liberté (les valeurs de sortie possibles de la régression sont le nombre de nœuds feuilles), mais pas assez pour être trop profond. Si vous ne le coupez pas, l'algorithme déjà très dispersé deviendra trop complexe en raison de la nature de la régression.
la mise en oeuvre
La régression d'arbre de décision peut être facilement créée dans
sklearn:
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(X_train, y_train)
Étant donné que les paramètres du régresseur d'arbre de décision sont très importants, il est recommandé d'utiliser un outil d'optimisation des paramètres des moteurs de recherche à
GridCVpartir de sklearn, pour trouver la bonne recommandation pour ce modèle.
Lors de l'évaluation formelle des performances, utilisez des tests
K-foldplutôt que des tests standard train-test-splitpour éviter le caractère aléatoire de ces derniers qui pourrait violer les résultats sensibles d'un modèle à variance élevée.
Prime: Un proche parent de l'arbre de décision, l'algorithme de forêt aléatoire, peut également être implémenté comme régresseur. Un régresseur forestier aléatoire peut ou non fonctionner mieux qu'un arbre de décision en régression (alors qu'il fonctionne généralement mieux en classification) en raison de l'équilibre délicat entre la redondance et la carence dans la nature des algorithmes de construction d'arbres.
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X_train, y_train)
3. Régression LASSO
La méthode de régression au lasso (LASSO, Least Absolute Shrinkage and Selection Operator) est une variante de la régression linéaire spécialement adaptée pour les données qui présentent une forte multicolinéarité (c'est-à-dire une forte corrélation des caractéristiques entre elles).
Il automatise certaines parties de la sélection de modèle telles que la sélection de variables ou l'exclusion de paramètres. LASSO utilise le rétrécissement, qui est un processus dans lequel les valeurs de données s'approchent d'un point central (comme une moyenne).

Illustration de l'auteur. Visualisation simplifiée du
processus de compression Le processus de compression ajoute plusieurs avantages aux modèles de régression:
- Estimations plus précises et stables des vrais paramètres.
- Réduire les erreurs d'échantillonnage et le hors-échantillonnage.
- Lissage des fluctuations spatiales.
Plutôt que d'ajuster la complexité du modèle pour compenser la complexité des données, comme les réseaux de neurones à variance élevée et les méthodes de régression par arbre de décision, le lasso tente de réduire la complexité des données afin qu'elles puissent être traitées par des méthodes de régression simples en courbant l'espace sur lequel elles se trouvent. Dans ce processus, le lasso aide automatiquement à éliminer ou déformer les caractéristiques hautement corrélées et redondantes dans une méthode à faible variance.
La régression au lasso utilise la régularisation L1, c'est-à-dire pondère les erreurs par leur valeur absolue. Au lieu, par exemple, de la régularisation L2, qui pèse les erreurs par leur carré, afin de punir plus fortement les erreurs les plus significatives.
Cette régularisation conduit souvent à des modèles plus clairsemés avec moins de coefficients, car certains coefficients peuvent devenir nuls et donc être exclus du modèle. Cela lui permet d'être interprété.
la mise en oeuvre
Le
sklearnlasso de régression est livré avec un modèle de validation croisée qui sélectionne le plus efficace des nombreux modèles entraînés avec différents paramètres fondamentaux et des parcours d'apprentissage qui automatisent une tâche qui, autrement, devrait être effectuée manuellement.
from sklearn.linear_model import LassoCV
model = LassoCV()
model.fit(X_train, y_train)
4. Régression de crête (régression de crête)
Théorie
La régression de crête ou régression de crête est très similaire à la régression LASSO en ce qu'elle applique une compression. Les deux algorithmes sont bien adaptés aux ensembles de données avec un grand nombre de caractéristiques qui ne sont pas indépendantes l'une de l'autre (colinéarité).
Cependant, la plus grande différence entre eux est que la régression de crête utilise la régression L2, c'est-à-dire qu'aucun des coefficients ne devient nul, tout comme la régression LASSO. Au lieu de cela, les coefficients se rapprochent de plus en plus de zéro, mais sont peu incités à l'atteindre en raison de la nature de la régularisation L2.
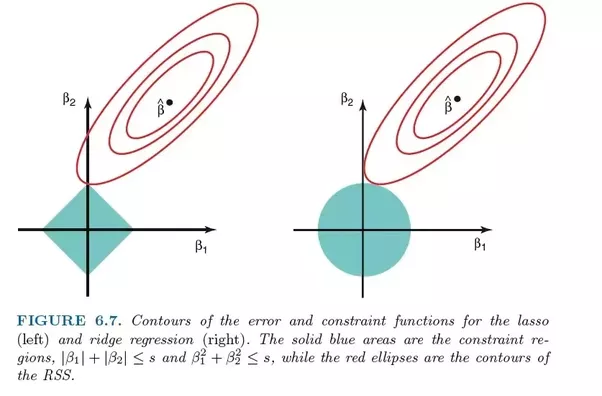
Comparaison des erreurs de régression au lasso (à gauche) et de régression de crête (à droite). Puisque la régression de crête utilise la régularisation L2, sa zone ressemble à un cercle, tandis que la régression du lasso L1 trace des lignes droites. Image libre. Source
Dans le lasso, l'amélioration de l'erreur 5 à l'erreur 4 est pondérée de la même manière que l'amélioration de 4 à 3, et également de 3 à 2, de 2 à 1 et de 1 à 0. Par conséquent, plus de coefficients atteignent zéro et plus de caractéristiques sont éliminées.
Cependant, dans la régression de crête, l'amélioration de l'erreur 5 à l'erreur 4 est calculée comme 5² - 4² = 9, tandis que l'amélioration de 4 à 3 est pondérée uniquement comme 7. Progressivement, la récompense de l'amélioration diminue; par conséquent, moins de fonctionnalités sont éliminées.
La régression Ridge est la mieux adaptée aux situations où nous voulons donner la priorité à un grand nombre de variables, dont chacune a un petit effet. Si votre modèle doit tenir compte de plusieurs variables, dont chacune a un effet moyen à important, le lasso est le meilleur choix.
la mise en oeuvre
La régression Ridge
sklearnpeut être implémentée comme suit (voir ci-dessous). Comme pour la régression par lasso, sklearnil existe une implémentation pour valider la sélection du meilleur de nombreux modèles entraînés.
from sklearn.linear_model import RidgeCV
model = Ridge()
model.fit(X_train, y_train)
5. Régression ElasticNet
Théorie
ElasticNet vise à combiner le meilleur de la régression de crête et de la régression de lasso en combinant les régularisations L1 et L2.
Lasso et Ridge Regression sont deux méthodes de régularisation différentes. Dans les deux cas, λ est le facteur clé qui contrôle le montant de l'amende:
- λ = 0, , .
- λ = ∞, - . , , .
- 0 < λ < ∞, λ , .
Au paramètre λ, la régression ElasticNet ajoute un paramètre supplémentaire α , qui mesure le degré de «mixité» des régularisations L1 et L2. Lorsque α est égal à 0, le modèle est une régression de crête pure, et lorsque α est égal à 1, il s'agit d'une régression de lasso pure.
Le «facteur de mélange» α définit simplement le degré de régularisation L1 et L2 à considérer dans la fonction de perte. Les trois modèles de régression populaires - Ridge, Lasso et ElasticNet - visent à réduire la taille de leurs coefficients, mais chacun agit différemment.
la mise en oeuvre
ElasticNet peut être implémenté à l'aide du modèle de validation croisée de sklearn:
from sklearn.linear_model import ElasticNetCV
model = ElasticNetCV()
model.fit(X_train, y_train)
Que lire d'autre sur le sujet:
- Analyse du Big Data dans le Cloud: comment une entreprise peut devenir axée sur les données.
- Formats de fichiers dans le Big Data.
- - .