Mais comment fonctionne exactement le suivi d'objets? Il existe de nombreuses solutions de Deep Learning pour ce problème, et aujourd'hui, je souhaite parler d'une solution commune et des mathématiques qui la sous-tendent.
Donc, dans cet article, je vais essayer de vous expliquer en termes simples et en formules:
- YOLO est un excellent détecteur d'objets
- Filtres Kalman
- Distance de Mahalanobis
- Tri en profondeur
YOLO est un excellent détecteur d'objets
Immédiatement, vous devez faire une note très importante dont vous devez vous souvenir: la détection d'objets n'est pas le suivi d'objets. Pour beaucoup, ce ne sera pas une nouvelle, mais souvent les gens confondent ces concepts. En termes simples: la
détection d'objets est simplement la définition d'objets dans l'image / le cadre. Autrement dit, un algorithme ou un réseau de neurones définit un objet et enregistre sa position et ses cadres de délimitation (paramètres des rectangles autour des objets). Jusqu'à présent, il n'est pas question d'autres cadres et l'algorithme ne fonctionne qu'avec un seul.
Exemple: le
suivi d'objets est une tout autre affaire. Ici, la tâche n'est pas seulement d'identifier les objets dans le cadre, mais aussi de lier les informations des cadres précédents de manière à ne pas perdre l'objet, ou à le rendre unique.
Exemple:

Autrement dit, Object Tracker inclut la détection d'objets pour déterminer les objets, et d'autres algorithmes pour comprendre quel objet sur une nouvelle image appartient à laquelle de l'image précédente.
Par conséquent, la détection d'objets joue un rôle très important dans la tâche de suivi.
Pourquoi YOLO? Oui, car YOLO est considéré comme plus efficace que de nombreux autres algorithmes pour identifier des objets. Voici un petit graphique de comparaison des créateurs de YOLO:
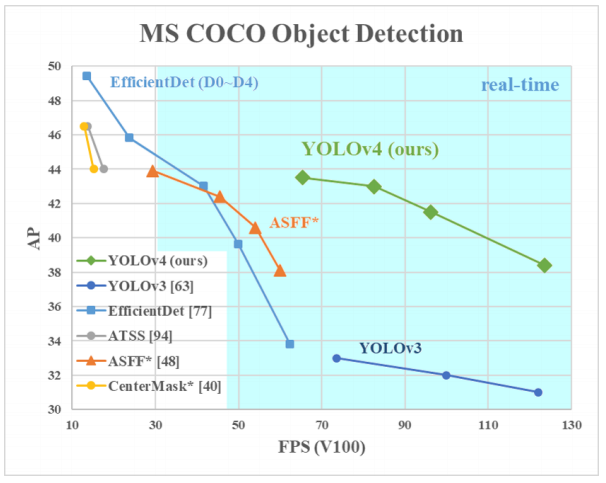
Ici, nous regardons YOLOv3-4 car ce sont les versions les plus récentes et sont plus efficaces que les précédentes.
Architectures de différents détecteurs d'objets
Ainsi, il existe plusieurs architectures de réseaux neuronaux conçues pour définir des objets. Ils sont généralement classés en «deux niveaux» tels que RCNN, RCNN rapide et RCNN plus rapide, et «à un niveau» comme YOLO.
Les réseaux neuronaux «à deux couches» énumérés ci-dessus utilisent les soi-disant régions dans l'image pour déterminer si un objet particulier se trouve dans cette région.
Cela ressemble généralement à ceci (pour un RCNN plus rapide, qui est le plus rapide des systèmes à deux niveaux répertoriés):
- L'image / le cadre est envoyé à l'entrée
- Le cadre est exécuté via CNN pour former des cartes de caractéristiques
- Un réseau neuronal distinct définit les régions avec une forte probabilité d'y trouver des objets
- Ensuite, en utilisant le regroupement RoI, ces régions sont compressées et introduites dans le réseau neuronal, qui détermine la classe de l'objet dans les régions

Mais ces réseaux de neurones ont deux problèmes majeurs: ils ne regardent pas la situation dans son ensemble, mais uniquement dans des régions individuelles, et ils sont relativement lents.
Qu'y a-t-il de si cool chez YOLO? Le fait que cette architecture ne présente pas deux problèmes d'en haut, et elle a prouvé à maintes reprises son efficacité.
En général, l'architecture YOLO dans les premiers blocs ne diffère pas beaucoup en termes de «logique de bloc» des autres détecteurs, c'est-à-dire qu'une image est transmise à l'entrée, puis des cartes de caractéristiques sont créées à l'aide de CNN (bien que YOLO utilise son propre CNN appelé Darknet-53), puis ces cartes de caractéristiques sont analysés d'une certaine manière (plus à ce sujet plus tard), donnant les positions et les tailles des boîtes englobantes et les classes auxquelles elles appartiennent.

Mais que sont le cou, la prédiction dense et la prédiction parcimonieuse?
Nous avons traité de Sparse Prediction un peu plus tôt - il s'agit simplement d'une réitération du fonctionnement des algorithmes à deux niveaux: ils définissent les régions individuellement, puis classent ces régions.
Neck (ou «neck») est un bloc séparé, qui est créé afin d'agréger les informations des couches séparées des blocs précédents (comme le montre la figure ci-dessus) pour augmenter la précision de la prédiction. Si cela vous intéresse, vous pouvez rechercher sur Google les termes "Réseau d'agrégation de chemins", "Module d'attention spatiale" et "Regroupement de pyramides spatiales".
Et enfin, ce qui distingue YOLO de toutes les autres architectures est un bloc appelé (dans notre image ci-dessus) Dense Prediction. Nous allons nous y attacher un peu plus, car c'est une solution très intéressante, qui vient de permettre à YOLO de devenir le leader de l'efficacité de la détection d'objets.
YOLO (You Only Look Once) porte la philosophie de regarder l'image une fois, et pour cette seule visualisation (c'est-à-dire une course de l'image à travers un réseau neuronal) pour faire toutes les définitions d'objet nécessaires. Comment cela peut-il arriver?
Donc, à la sortie du travail de YOLO, nous voulons généralement ceci:
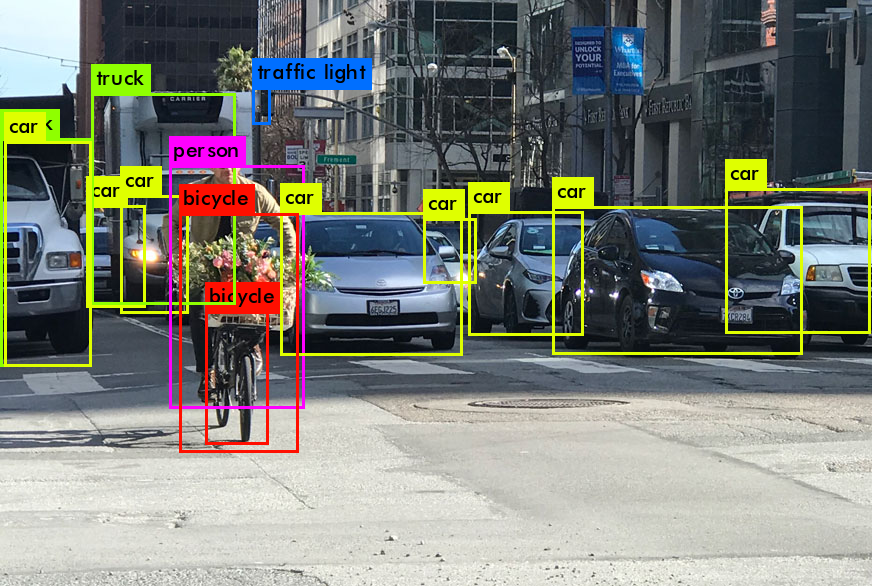
Que fait YOLO quand il apprend à partir de données (en termes simples):
Étape 1: Habituellement, les images seront remodelées à une taille de 416x416 avant d'entraîner le réseau neuronal, afin qu'elles puissent être alimentées par lots (pour accélérer l'apprentissage ).
Étape 2: Divisez l'image (pour l'instant mentalement) en cellules de taille a x a . Dans YOLOv3-4, il est d'usage de se diviser en cellules de taille 13x13 (nous parlerons de différentes échelles un peu plus tard pour le rendre plus clair).

Concentrons-nous maintenant sur ces cellules, dans lesquelles nous avons divisé l'image / le cadre. Ces cellules, appelées cellules de grille, sont au cœur de l'idée YOLO. Chaque cellule est une «ancre» à laquelle sont attachés des cadres de délimitation. Autrement dit, plusieurs rectangles sont dessinés autour de la cellule pour définir l'objet (comme on ne sait pas quelle forme le rectangle conviendra le mieux, ils sont dessinés à la fois dans plusieurs formes différentes), et leurs positions, largeur et hauteur sont calculées par rapport au centre de cette cellule.
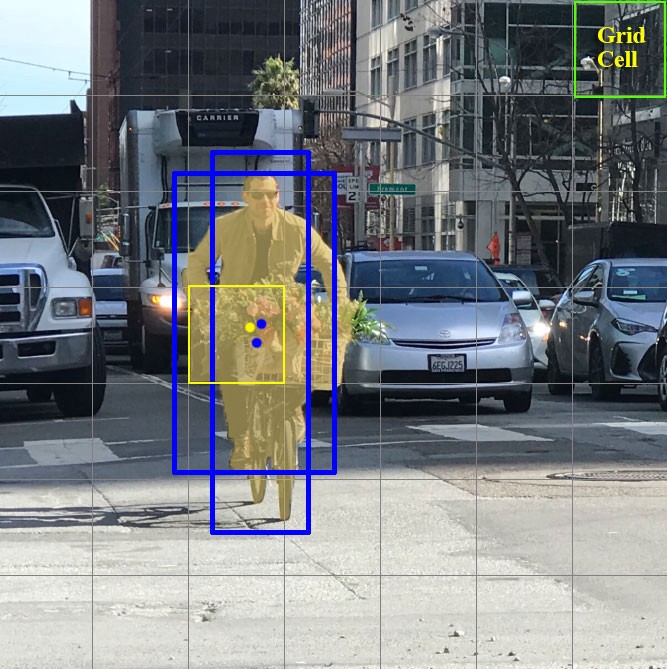
Comment ces boîtes de délimitation sont-elles dessinées autour de la cage? Comment leur taille et leur position sont-elles déterminées? C'est là que la technique des boîtes d'ancrage (en traduction - boîtes d'ancrage, ou «rectangles d'ancrage») entre en jeu. Ils sont définis au tout début soit par l'utilisateur lui-même, soit leurs tailles sont déterminées en fonction des tailles des boîtes englobantes qui se trouvent dans le jeu de données sur lequel YOLO va s'entraîner (le clustering K-means et l'IoU sont utilisés pour déterminer les tailles les plus appropriées). Habituellement, il y a 3 boîtes d'ancrage différentes à dessiner autour (ou à l'intérieur) d'une cellule:

pourquoi est-ce fait? Ce sera clair maintenant lorsque nous discuterons de la façon dont YOLO apprend.
Étape 3. L'image de l'ensemble de données est exécutée à travers notre réseau neuronal (notez qu'en plus de l'image dans l'ensemble de données d'entraînement, nous devons avoir les positions et les tailles des vraies boîtes englobantes pour les objets qu'il contient. Cela s'appelle "annotation" et se fait principalement manuellement ).
Pensons maintenant à ce que nous devons obtenir en sortie.
Pour chaque cellule, nous devons comprendre deux choses fondamentales:
- Laquelle des 3 boîtes d'ancrage dessinées autour de la cage nous convient le mieux, et comment pouvons-nous la modifier un peu pour qu'elle s'adapte bien à l'objet
- Quel objet se trouve à l'intérieur de cette boîte d'ancrage et y est-il du tout
Quelle devrait alors être la sortie de YOLO?
1. À la sortie de chaque cellule, nous voulons obtenir:

2. La sortie doit inclure les paramètres suivants:
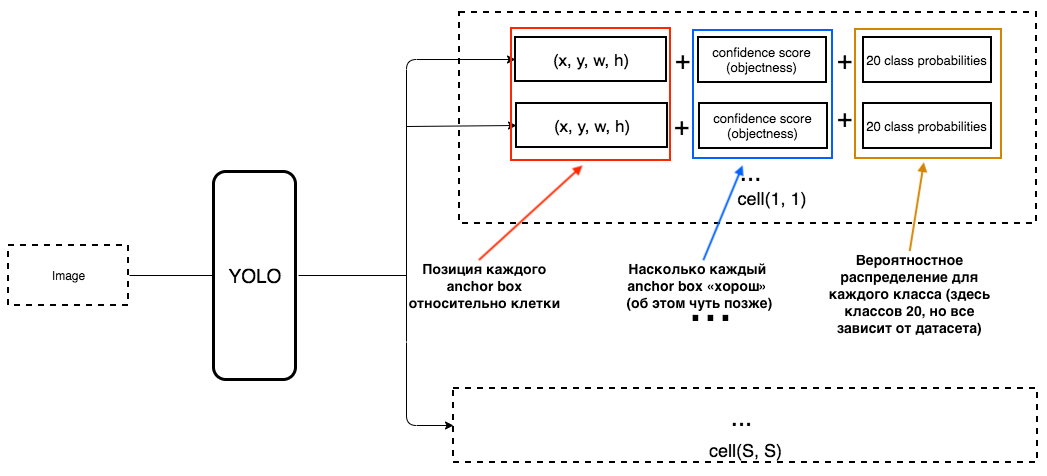
Comment l'objectivité est-elle déterminée? En fait, ce paramètre est déterminé à l'aide de la métrique IoU pendant l'entraînement. La métrique IoU fonctionne comme ceci:
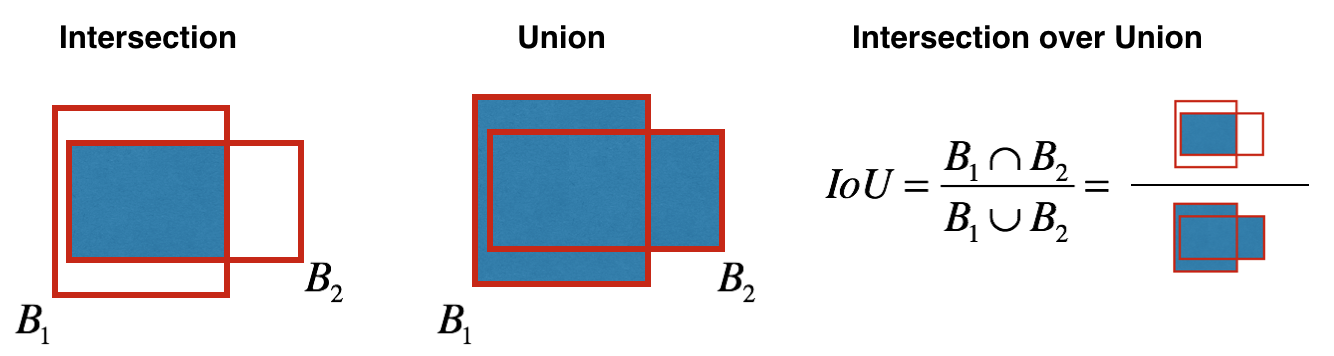
au début, vous pouvez définir un seuil pour cette métrique, et si votre boîte englobante prévue est supérieure à ce seuil, alors elle aura une objectivité égale à un, et toutes les autres boîtes englobantes avec une objectivité inférieure seront exclues. Nous aurons besoin de cette valeur d'objectivité lorsque nous calculons le score de confiance global (dans quelle mesure sommes-nous sûrs que l'objet dont nous avons besoin est situé à l'intérieur du rectangle prédit) pour chaque objet spécifique.
Et maintenant, le plaisir commence. Imaginons que nous sommes les créateurs de YOLO et que nous devons la former à reconnaître les personnes dans le cadre / l'image. Nous transmettons l'image du jeu de données à YOLO, où l'extraction d'entités se produit au début, et à la fin, nous obtenons une couche CNN qui nous informe de toutes les cellules dans lesquelles nous avons «divisé» notre image. Et si cette couche nous dit un "mensonge" sur les cellules de l'image, alors nous devons avoir une grande perte, de sorte que plus tard elle puisse être réduite lorsque les images suivantes sont introduites dans le réseau neuronal.
Pour être très clair, il existe un schéma très simple de la façon dont YOLO crée cette dernière couche:
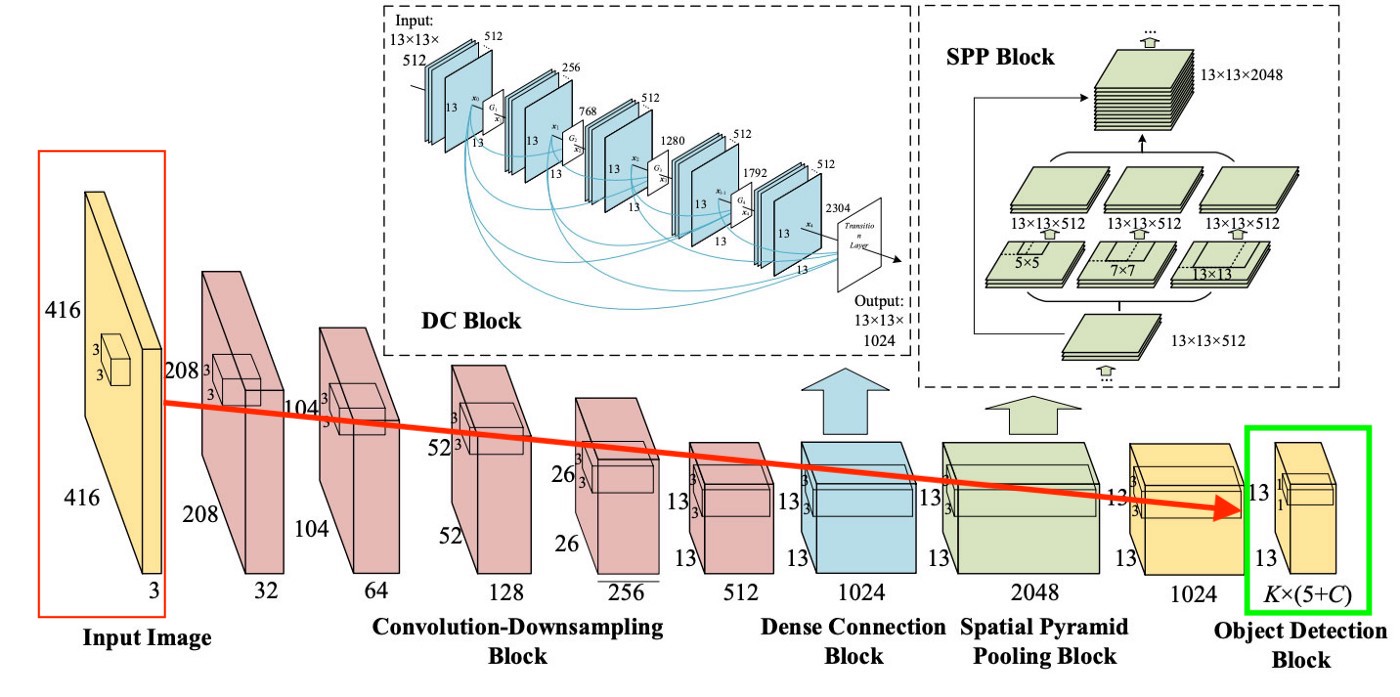
Comme on peut le voir sur l'image, cette couche est de 13x13 (pour les images, la taille initiale est de 416x416) afin de parler de "chaque cellule" dans l'image. A partir de cette dernière couche, les informations que nous voulons sont obtenues.
YOLO prédit 5 paramètres (pour chaque case d'ancrage pour une cellule spécifique):

Pour faciliter la compréhension, il existe une bonne visualisation sur ce sujet:

Comme vous pouvez les comprendre à partir de cette image, la tâche de YOLO est de prédire ces paramètres aussi précisément que possible afin de déterminer l'objet de l'image aussi précisément que possible. Et le score de confiance, qui est déterminé pour chaque boîte englobante prédite, est une sorte de filtre afin de filtrer les prédictions complètement inexactes. Pour chaque boîte englobante prédite, nous multiplions son IoU par la probabilité qu'il s'agisse d'un certain objet (la distribution de probabilité est calculée pendant l'entraînement du réseau de neurones), nous prenons la meilleure probabilité de tout possible, et si le nombre après multiplication dépasse un certain seuil, nous pouvons laisser cette prédiction cadre de sélection dans l'image.
De plus, lorsque nous avons seulement prédit des boîtes englobantes avec un score de confiance élevé, nos prédictions (si visualisées) peuvent ressembler à ceci:

nous pouvons maintenant utiliser la technique NMS (non-max suppression) pour filtrer les boîtes englobantes de telle manière que pour d'un objet, il n'y avait qu'une seule boîte englobante prévue.

Sachez également que YOLOv3-4 est prédit sur 3 échelles différentes. Autrement dit, l'image est divisée en 64 cellules de grille, 256 cellules et 1024 cellules afin de voir également les petits objets. Pour chaque groupe de cellules, l'algorithme répète les actions nécessaires lors de la prédiction / apprentissage, qui ont été décrites ci-dessus.
De nombreuses techniques ont été utilisées dans YOLOv4 pour augmenter la précision du modèle sans perdre trop de vitesse. Mais pour la prédiction elle-même, Dense Prediction est restée la même que dans YOLOv3. Si vous vous demandez ce que les auteurs ont fait de manière magique pour augmenter la précision sans perdre de vitesse, il existe un excellent article écrit sur YOLOv4 .
J'espère avoir réussi à transmettre un peu le fonctionnement de YOLO en général (plus précisément les deux dernières versions, c'est-à-dire YOLOv3 et YOLOv4), et cela éveillera en vous l'envie d'utiliser ce modèle à l'avenir, ou d'en apprendre un peu plus sur son travail.
Maintenant que nous avons déterminé quel est peut-être le meilleur réseau neuronal pour la détection d'objets (en termes de vitesse / qualité), passons enfin à la façon dont nous pouvons associer des informations sur nos objets YOLO spécifiques entre les images vidéo. Comment le programme peut-il comprendre que la personne dans le cadre précédent est la même personne que dans la nouvelle?
Tri en profondeur
Pour comprendre cette technologie, vous devez d'abord comprendre quelques aspects mathématiques - la distance de Mahalonobis et le filtre de Kalman.
Distance de Mahalonobis Prenons
un exemple très simple pour comprendre intuitivement ce qu'est la distance de Maholonobis et pourquoi elle est nécessaire. Beaucoup de gens savent probablement quelle est la distance euclidienne. Habituellement, c'est la distance d'un point à un autre dans l'espace euclidien:
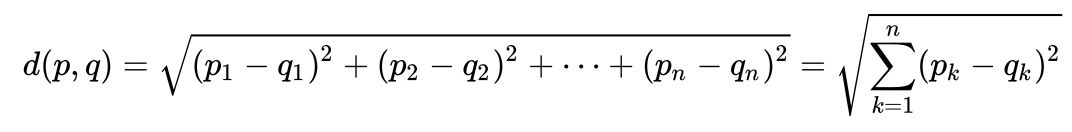

disons que nous avons deux variables - X1 et X2. Pour chacun d'eux, nous avons de nombreuses dimensions.
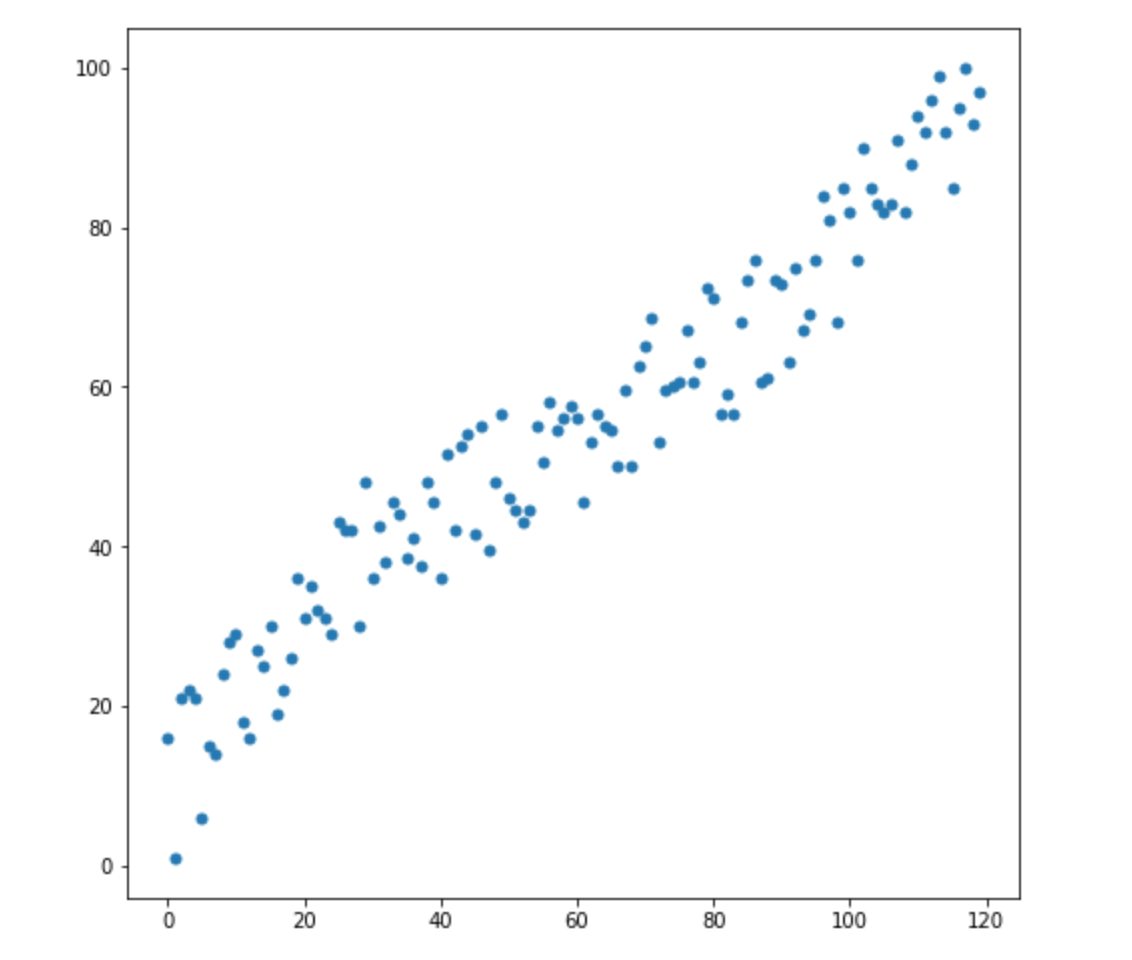
Maintenant, disons que nous avons 2 nouvelles dimensions:
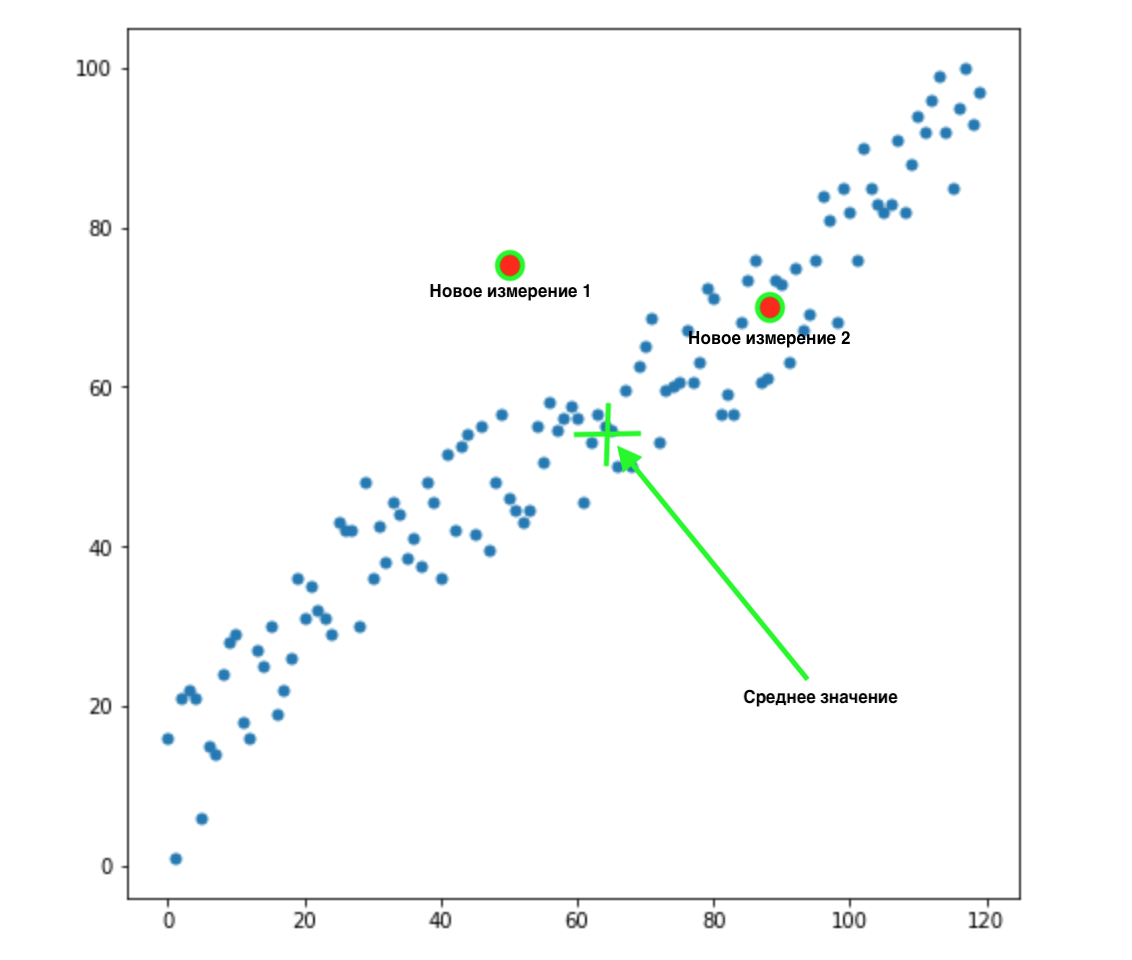
Comment savoir laquelle de ces deux valeurs est la plus appropriée pour notre distribution? Tout est évident à l'œil nu - le point 2 nous convient. Mais la distance euclidienne à la moyenne est la même pour les deux points. En conséquence, une simple distance euclidienne à la moyenne ne fonctionnera pas pour nous.
Comme nous pouvons le voir sur l'image ci-dessus, les variables sont corrélées les unes aux autres, et assez fortement. S'ils n'étaient pas corrélés entre eux, ou beaucoup moins corrélés, nous pourrions fermer les yeux et appliquer la distance euclidienne pour certaines tâches, mais ici nous devons corriger la corrélation et la prendre en compte.
C'est exactement ce que peut supporter la distance de Mahalonobis. Comme il y a généralement plus de deux variables dans les ensembles de données, nous utiliserons une matrice de covariance au lieu de la corrélation:
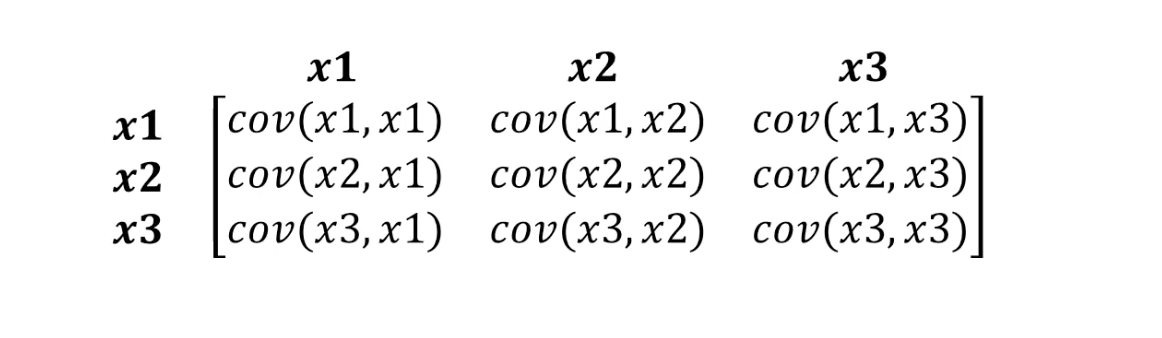
Ce que fait réellement la distance de Mahalonobis:
- Débarrassez-vous de la covariance variable
- Rend la variance des variables égale à 1
- Ensuite, il utilise la distance euclidienne habituelle pour les données transformées.
Regardons la formule de calcul de la distance de Mahalonobis:

Voyons ce que signifient les composants de notre formule:
- Cette différence est la différence entre notre nouveau point et les moyennes de chaque variable.
- S est la matrice de covariance dont nous avons parlé un peu plus tôt.
Une chose très importante peut être comprise à partir de la formule. Nous multiplions en fait par la matrice de covariance inversée. Dans ce cas, plus la corrélation entre les variables est élevée, plus nous réduirons probablement la distance, car nous multiplierons par l'inverse du plus grand - c'est-à-dire le plus petit nombre (si c'est en termes simples).
Nous n'entrerons probablement pas dans les détails de l'algèbre linéaire, il suffit de comprendre que nous mesurons la distance entre les points de manière à prendre en compte la variance de nos variables et la covariance entre eux.
Filtre de Kalman
Pour se rendre compte que c'est une chose cool et éprouvée qui peut être appliquée dans tant de domaines, il suffit de savoir que le filtre Kalman a été utilisé dans les années 1960. Oui, oui, je fais allusion à ceci - le vol vers la lune. Il y a été appliqué à plusieurs endroits, notamment en travaillant avec des trajectoires de vol aller-retour. Le filtre de Kalman est également souvent utilisé dans l'analyse de séries chronologiques sur les marchés financiers, dans l'analyse d'indicateurs de divers capteurs dans les usines, les entreprises et bien d'autres endroits. J'espère avoir réussi à vous intriguer un peu et nous décrirons brièvement le filtre Kalman et son fonctionnement. Je vous conseille également de lire cet article sur Habré si vous souhaitez en savoir plus.
Filtre de Kalman
, . , , .
, . 4 . , 72 .
3 :
1) (Kalman Gain):

, - ( ).
2) , ( , ), , .

3) (), :
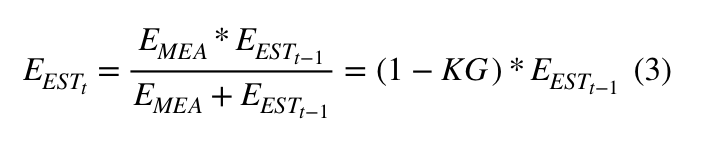
, :
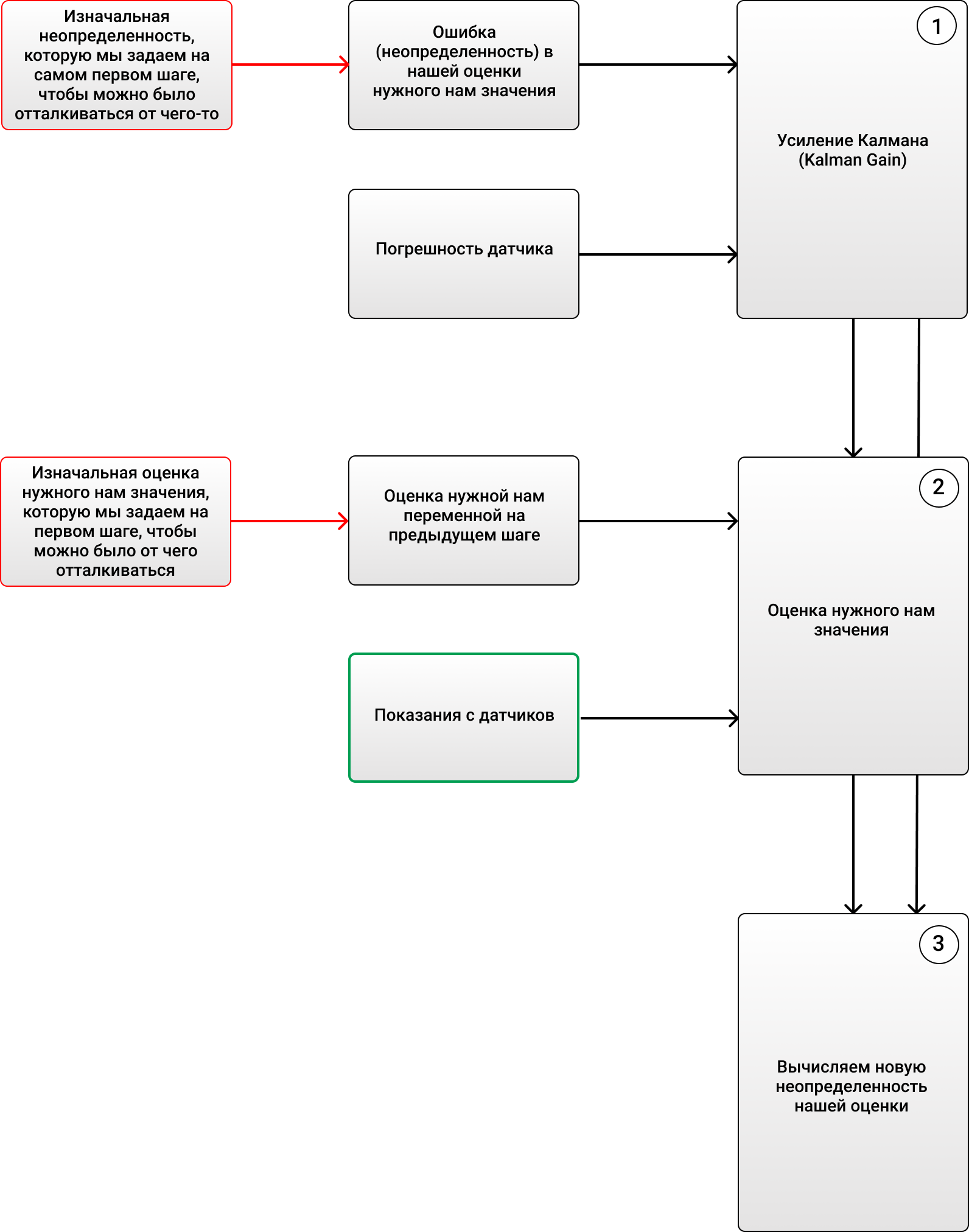
, 69 ( ), 2 . , , 4 (, , ), KG (1) 2/(2+4) = 0.33. ( ), . 70 (), . (2), , 68+0.33(70-68)=68.66. (3) (1-0.33)2 = 1.32. , , , . :
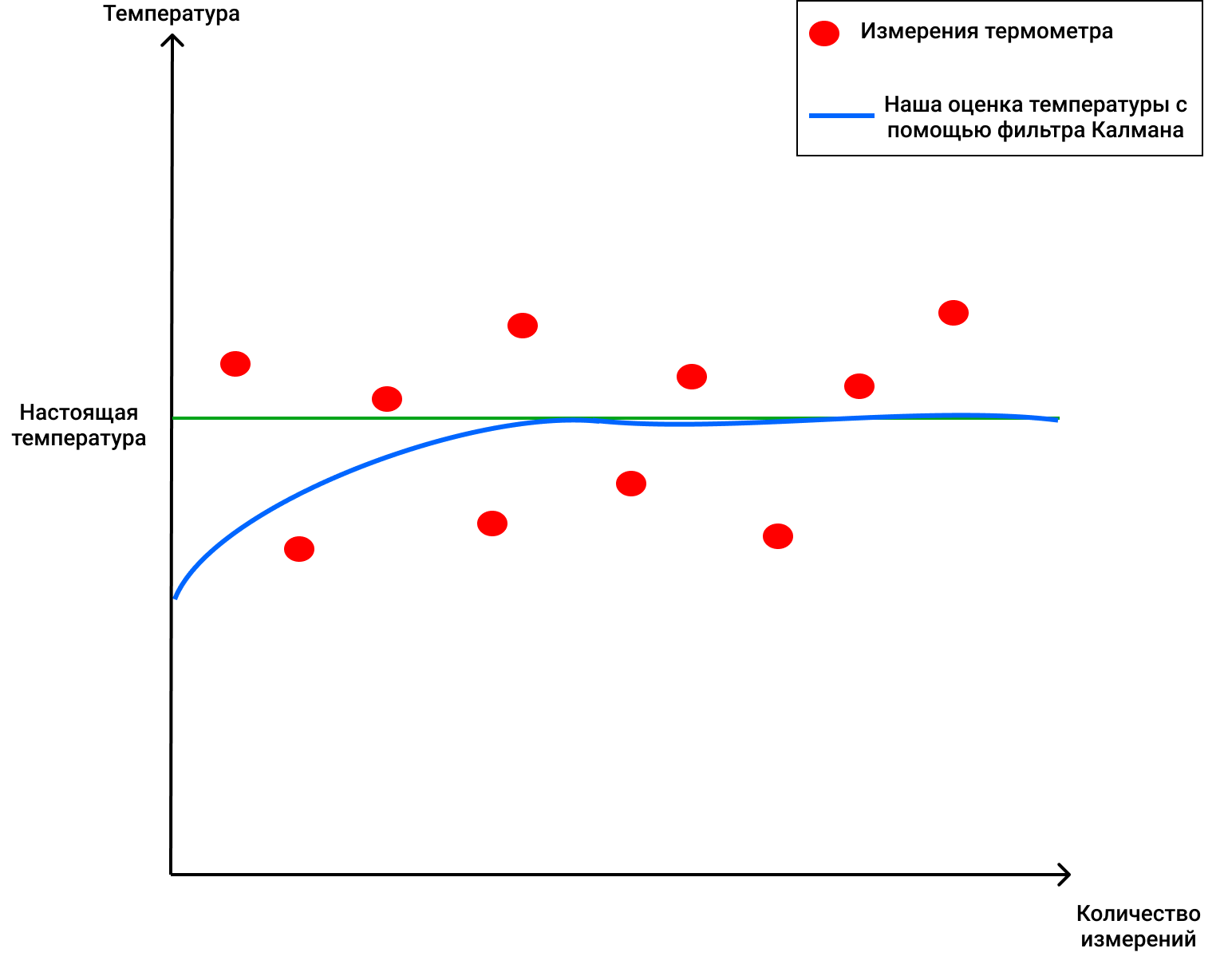
, !
, , , , , ( , ).
, . 4 . , 72 .
3 :
1) (Kalman Gain):

, - ( ).
2) , ( , ), , .

3) (), :
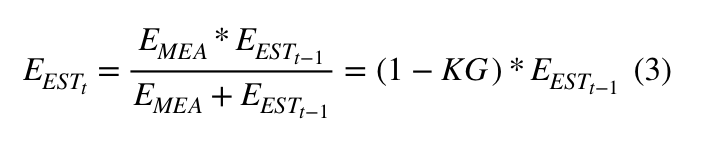
, :

, 69 ( ), 2 . , , 4 (, , ), KG (1) 2/(2+4) = 0.33. ( ), . 70 (), . (2), , 68+0.33(70-68)=68.66. (3) (1-0.33)2 = 1.32. , , , . :

, !
, , , , , ( , ).
DeepSORT - enfin!
Ainsi, nous savons maintenant ce que sont le filtre de Kalman et la distance de Mahalonobis. La technologie DeepSORT relie simplement ces deux concepts afin de transférer des informations d'une image à une autre, et ajoute une nouvelle métrique appelée apparence. Tout d'abord, à l'aide de la détection d'objet, la position, la taille et la classe d'un cadre de sélection sont déterminées. Ensuite, vous pouvez, en principe, appliquer l' algorithme hongrois pour associer certains objets à des ID d'objet qui étaient auparavant sur le cadre et suivis à l'aide de filtres de Kalman - et tout sera super, comme dans le SORT d'origine... Mais la technologie DeepSORT permet d'améliorer la précision de détection et de réduire le nombre de commutations entre les objets, lorsque, par exemple, une personne dans le cadre en bloque brièvement une autre, et maintenant la personne qui était obstruée est considérée comme un nouvel objet. Comment fait-elle ça?
Elle ajoute un élément cool à son travail - la soi-disant «apparence» des personnes qui apparaissent dans le cadre (apparence). Ce look a été formé par un réseau de neurones distinct créé par les auteurs de DeepSORT. Ils ont utilisé environ 1100000 images de plus de 1000 personnes différentes pour que le réseau neuronal prédise correctementLe TRI d'origine a un problème - puisque l'apparence de l'objet n'est pas utilisée là-bas, en fait, lorsque l'objet couvre quelque chose pour plusieurs cadres (par exemple, une autre personne ou une colonne à l'intérieur d'un bâtiment), l'algorithme attribue alors un autre identifiant à cette personne - en conséquence dans lequel la soi-disant «mémoire» des objets dans le SORT original est plutôt de courte durée.
Alors maintenant, les objets ont deux propriétés - leur dynamique de mouvement et leur apparence. Pour la dynamique, nous avons des indicateurs qui sont filtrés et prédits à l'aide du filtre de Kalman - (u, v, a, h, u ', v', a ', h'), où u, v est la position X du rectangle prédit et Y, a est le rapport hauteur / largeur du rectangle prédit, h est la hauteur du rectangle et les dérivées par rapport à chaque valeur. Pour l'apparence, un réseau de neurones a été formé, qui avait la structure:
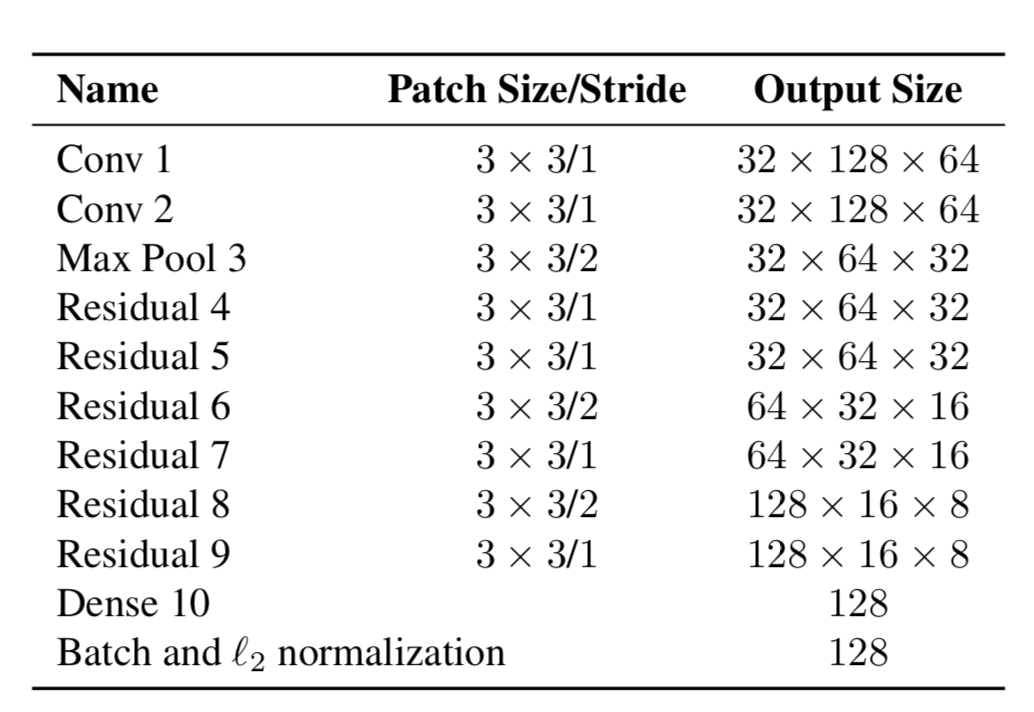
Et à la fin, il a donné un vecteur de caractéristiques, de taille 128x1. Et puis, au lieu de calculer la distance entre certains objets à l'aide de YOLO et des objets que nous avons déjà suivis dans le cadre, puis d'attribuer un certain identifiant simplement en utilisant la distance de Mahalonobis, les auteurs ont créé une nouvelle métrique pour calculer la distance, qui comprend les deux prédictions utilisant des filtres de Kalman, et la "distance cosinus", comme on l'appelle autrement, le coefficient d'Otiai.
En conséquence, la distance d'un certain objet YOLO à l'objet prédit par le filtre de Kalman (ou un objet qui est déjà parmi ceux qui ont été observés dans les images précédentes) est:

Où Da est la distance de similitude externe et Dk est la distance de Mahalonobis. De plus, cette distance hybride est utilisée dans l'algorithme hongrois afin de trier correctement certains objets avec des identifiants existants.
Ainsi, une simple métrique supplémentaire Da a aidé à créer un nouvel algorithme DeepSORT élégant qui est utilisé dans de nombreux problèmes et est très populaire dans le problème de suivi d'objets.
L'article s'est avéré assez lourd, grâce à ceux qui ont lu jusqu'au bout! J'espère avoir pu vous dire quelque chose de nouveau et vous aider à comprendre comment fonctionne le suivi d'objets sur YOLO et DeepSORT.