Deux mathématiciens prouvent la première étape de la conjecture préférée d'Erds sur les motifs dans les séquences de nombres

Un couple de mathématiciens a prouvé la première partie de l'une des hypothèses les plus célèbres concernant les propriétés additives des nombres entiers. Il a été proposé il y a plus de 60 ans par le légendaire mathématicien hongrois Pal Erdos . Cela ressemble à ceci: à quel point dans une liste infinie d'entiers sont garantis des modèles d'au moins trois nombres espacés à la même distance les uns des autres - par exemple, 26, 29 et 32.
Erdos a formulé des milliers de problèmes au cours de sa carrière, mais la question est, quelle liste de nombres contient des nombres équidistants les uns des autres (ce que les mathématiciens appellent des progressions arithmétiques) était l'un de ses favoris. «Je pense que beaucoup de gens ont vu cela comme la principale préoccupation d'Erds», a déclaré Timothy Gowers de l'Université de Cambridge. Gowers, qui a reçuFields Prize en 1998, a passé de nombreuses heures à essayer de résoudre ce problème. «Presque toutes les combinatoires additives assez ambitieuses ont essayé de le résoudre», a-t-il dit, se référant à la branche des mathématiques à laquelle appartient cette hypothèse.
Les listes de nombres plus denses sont généralement plus susceptibles de contenir une progression arithmétique que les listes clairsemées. Par conséquent, Erds a proposé une simple vérification de la densité d'une liste: ajouter les valeurs inverses de celles de la liste. S'il y a suffisamment de nombres pour rendre cette somme infinie, alors, selon l'hypothèse d'Erdos, la liste devrait contenir un nombre infini de progressions arithmétiques de toute longueur finie - trois, quatre, etc. numéros d'affilée.
Dans un article publié en ligne le 7 juillet par Thomas Bloom de Cambridge et Olaf Sisaskde l'Université de Stockholm a prouvé cette hypothèse dans le cas de triplets de nombres régulièrement espacés - tels que 5, 7 et 9. Cette paire a montré que lorsque la somme des réciproques des nombres d'une liste est infinie, il doit y avoir une infinité de triplets de nombres également espacés.

Thomas Bloom de Cambridge
«C'est le résultat le plus remarquable depuis de nombreuses années», a déclaré Nets Katz du California Institute of Technology. "C'est un événement important."
L'un des ensembles, dont la somme des nombres réciproques tend vers l'infini, sont des nombres premiers - ceux qui ne sont divisibles que par 1 et eux-mêmes. Dans les années 1930 Johannes van der Corpututilisé une structure spéciale de nombres premiers pour montrer que vous pouvez en effet trouver un nombre infini de triplets également espacés (par exemple, 17, 23 et 29).
Cependant, la nouvelle découverte de Bloom et Sisask signifie que l'on n'a pas besoin de comprendre en profondeur la structure unique des nombres premiers pour prouver qu'il y a un nombre infini de triplets en eux. Il suffit de savoir qu'il y a suffisamment de nombres premiers pour que la somme de leurs valeurs réciproques soit infinie - et cela est connu des mathématiciens depuis de nombreux siècles. «Le résultat de Thomas et Olaf nous dit que même si leur structure était complètement différente de ce qu'ils ont réellement, le simple fait d'en avoir un grand nombre garantirait une infinité de progressions arithmétiques», nous écrit Tom Sanders.de l'Université d'Oxford.
Le nouvel ouvrage fait 77 pages et il faudra un certain temps aux mathématiciens pour le vérifier en profondeur. Cependant, beaucoup sont optimistes à ce sujet. "Il semble vraiment que la preuve de cette affirmation devrait ressembler", a déclaré Katz, dont les premiers travaux ont constitué la base de cela.
Le théorème de Bloom et Sisask dit que si la liste des nombres est suffisamment dense, certains modèles devraient y apparaître. Cette découverte est cohérente avec la devise fondamentale des mathématiques, comme l' appelle Sarah Pillus d'Oxford, formulée pour la première fois par Theodore Motzkin: «Il n'y a pas de désordre absolu».
Densité déguisée
Il est assez facile de créer une liste infinie sans progressions arithmétiques si vous la réduisez suffisamment. Par exemple, considérons la séquence 1, 10, 100, 1 000, 10 000, ... Les réciproques totalisent 1,111 (1). La distance entre ces nombres croît si vite que pas un seul triplet de nombres situés à égale distance les uns des autres ne peut être trouvé.
Cependant, vous vous demandez peut-être s'il existe une liste plus dense de nombres qui n'ont toujours pas de progressions arithmétiques. Vous pouvez, par exemple, marcher le long d'une droite numérique et laisser chaque nombre qui n'est pas inclus dans les progressions arithmétiques. On obtient la séquence 1, 2, 4, 5, 10, 11, 13, 14, ... qui à première vue semble assez dense. Cependant, au fil du temps, cela devient de plus en plus rare - par exemple, lorsque nous obtenons des nombres à 20 chiffres, nous ne prendrons que 0,000009% de tous les entiers de la droite numérique. En 1946, Felix Berend a proposé des exemples plus denses, mais ils deviennent aussi rares très rapidement - l'ensemble de Berend, atteignant des nombres à 20 chiffres, ne contient que 0,001% de tous les entiers.
D'un autre côté, si votre ensemble contient presque tous les nombres entiers, alors il contiendra certainement des séquences arithmétiques. Mais entre ces deux extrêmes se trouve un territoire intermédiaire vaste, presque non marqué. Dans quelle mesure un ensemble peut-il être rare, ont spéculé les mathématiciens, de sorte que les progressions arithmétiques pourraient encore y être garanties?

Olaf Sisask de l'Université de Stockholm
Erdos (comme on dit, peut-être en collaboration avec le mathématicien hongrois Pal Turan) a donné une réponse possible. Sa condition pour la somme des réciproques est la densité masquée. Il s'avère que cela revient à dire que la densité d'une liste jusqu'au nombre N n'est pas inférieure à un divisé par le nombre de chiffres de N. En d'autres termes, votre liste peut devenir de plus en plus clairsemée à mesure que vous vous déplacez le long de la droite numérique, mais seulement si cela se produit très lentement. Sur les nombres à 5 chiffres, la densité de votre liste doit être d'au moins 1/5; sur 20 chiffres - au moins 1/20, et ainsi de suite. Et si cette condition est remplie, alors, comme Erdos l'a suggéré, votre liste devrait contenir un nombre infini de progressions arithmétiques de n'importe quelle longueur.
En 1953, Klaus Roth a mis les mathématiciens sur la voie menant à la preuve de la conjecture d'Erds. Dans un article qui lui a valu un prix Fields cette année-là, il a défini une fonction de densité qui garantit des triplets équidistants de nombres. La densité n'était pas aussi faible que celle d'Erds, mais elle s'approchait néanmoins de zéro lorsque nous nous déplacions le long de la droite numérique. Le théorème de Roth signifiait que dans la liste des nombres dont la densité tombe finalement en dessous de 1%, puis en dessous de 0,1%, puis en dessous de 0,01%, et ainsi de suite, il doit y avoir des progressions arithmétiques, si seulement sa densité baisse suffisamment lent.

Conférence de Pal Erds «60 ans en mathématiques» à l'Université de Cambridge en juin 1991.
Tout d'abord, l'approche de Roth était basée sur le fait que la plupart des listes avec la densité qu'il a choisie «veulent» avoir des progressions arithmétiques - elles ont suffisamment de paires de nombres différentes pour que presque certainement certains des points médians entre ces paires apparaissent également dans cette liste, qui conduirait à l'apparition de triplés également espacés. L'astuce est de savoir comment passer d'une liste de «presque tous» nombres à une liste de «tous» nombres, même si la structure entière aurait pu être spécialement conçue pour éviter les progressions arithmétiques.
Ayant reçu une telle liste, Roth a compris comment "distiller" sa structure en marquant son "spectre de fréquences" à l' aide de la transformée de Fourier... Il montre lesquels des modèles émergents sont les plus prononcés - les mêmes mathématiques sous-tendent des technologies telles que la cristallographie aux rayons X et la radiospectroscopie.
Certaines fréquences semblent plus fortes que d'autres, et ces variations soulignent les modèles existants - par exemple, la fréquence peut indiquer que la liste contient plus de nombres impairs que de nombres pairs. Si tel est le cas, vous pouvez vous concentrer uniquement sur les nombres impairs et obtenir une liste plus dense par rapport à une liste de nombres impairs uniquement. Roth a pu montrer qu'après plusieurs distillations de ce type, une liste serait si dense que des progressions arithmétiques devraient y être présentes.
L'approche de Roth a inspiré de nombreux articles en théorie analytique des nombres au cours des cinquante dernières années, déclare Jacob Fox de l'Université de Stanford. "Ses idées étaient très influentes."
Jeu, set, match
Cependant, la méthode de Roth ne fonctionnait que pour les ensembles de nombres qui étaient déjà assez denses depuis le début - sinon, des distillations constantes évaporeraient simplement tous les nombres. D'autres mathématiciens trouvaient constamment des moyens d'utiliser cette méthode de plus en plus efficacement, mais ils ne pouvaient pas s'approcher de la densité décrite dans l'hypothèse d'Erd. «Cet obstacle a semblé très difficile», a déclaré Fox.
Puis en 2011, Katz et Michael Bateman ont compris comment surmonter cet obstacle en termes plus simples: dans le jeu de cartes Seth, où les joueurs recherchent des ensembles de trois cartes marquées de différents symboles. Trois du jeu Set peuvent être définis comme une progression arithmétique, et, comme dans le cas d'une liste d'entiers, vous pouvez poser la question de savoir quelle fraction de toutes les cartes vous devez poser sur la table pour en trouver sûrement au moins trois.
Jeu "Set"
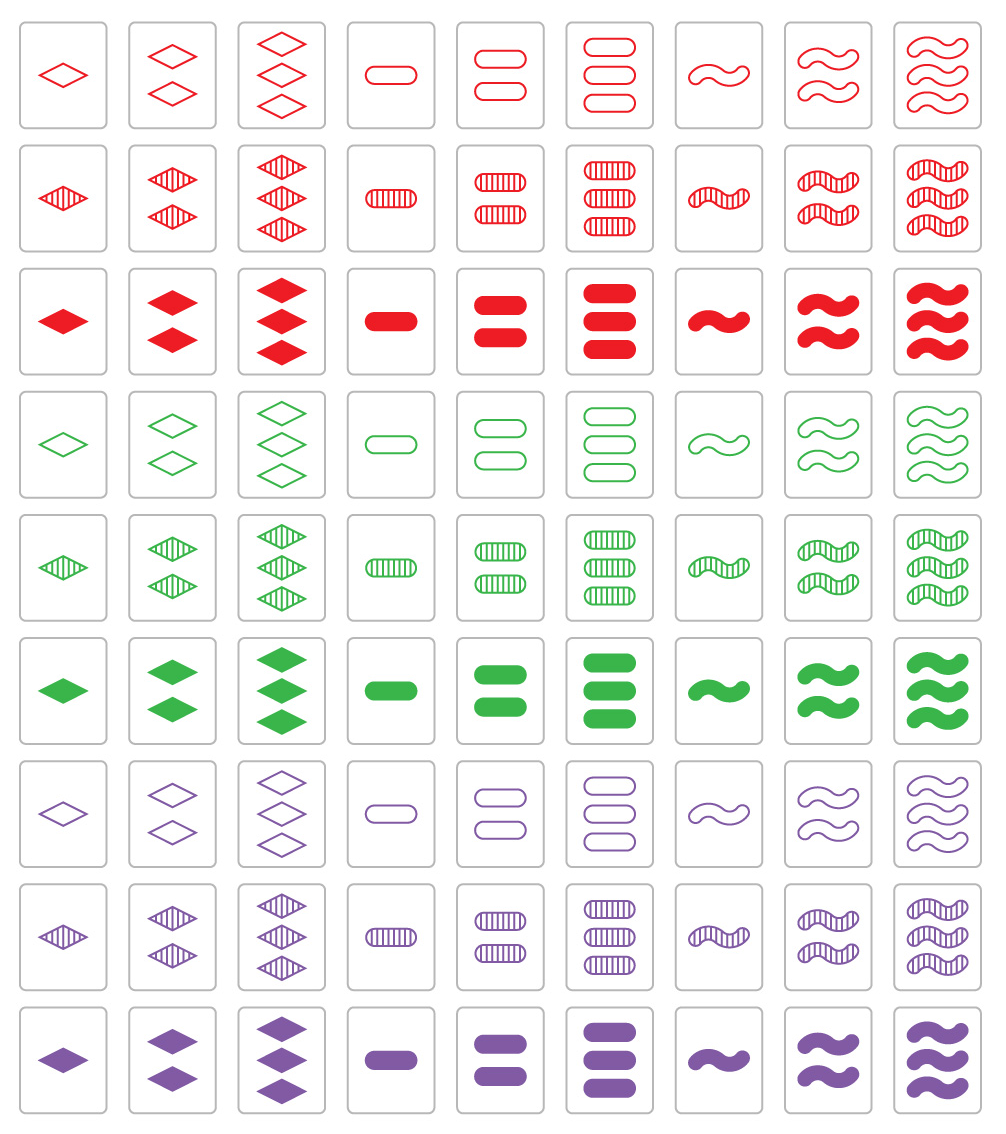
Le but du jeu est de trouver des triplets spéciaux de cartes, ou «ensembles», dans un jeu de 81 cartes. Chaque carte a son propre dessin avec quatre propriétés - la couleur (rouge, violet, vert), la forme (ovale, losange, vague), l'ombrage (contour, rayures, complètement rempli) et le nombre de formes (une, deux ou trois). En jeu normal, 12 cartes sont distribuées face visible sur la table, et les joueurs recherchent des ensembles de trois cartes dans lesquelles chacun des quatre attributs est soit le même pour toutes les cartes, soit différent pour toutes les cartes. S'il n'y a pas de tels ensembles parmi les 12 cartes, d'autres cartes sont ajoutées.
Pont entier
, –
| ? |  |
 |
 |
 |
Un moyen simple de collecter un jeu de cartes suffisamment grand sans triplés est de ne prendre que des cartes qui n'ont que deux ou trois choix pour chaque attribut. La taille de cette collection sera (2/3) n de l'ensemble du jeu, où n est le nombre d'attributs.

Cette question (liée non seulement au jeu Set standard, mais aussi à ses versions plus grandes) est un modèle naturel pour étudier la question correspondante concernant les entiers. Par conséquent, les mathématiciens espéraient que la percée de Bateman et Katz pourrait ouvrir la voie à la démonstration de la conjecture d'Erd s, en particulier lorsqu'elle était combinée avec d' autres percées récentes . Peu de temps après la sortie du travail de Bateman et Katz, Gowers a lancé le « projet polymath"- une collaboration conjointe massive a été conçue pour faire cette tentative.
Cependant, le projet a rapidement stagné". Il a rassemblé une énorme quantité d'arguments techniques, - a-t-il dit Gowers -. Ce projet est plus adapté à une ou deux personnes, pendant longtemps et en travaillant lentement. ".
Par Heureusement, quelques mathématiciens se préparaient juste à cela. Bloom et Sisask, au début séparément, ont déjà commencé à réfléchir à l'hypothèse d'Erds, captivés par la beauté des techniques utilisées. "C'était l'un des premiers problèmes de recherche auxquels j'ai été confronté", a déclaré Sisask , qui, comme Bloom, a maintenant environ 35 ans.
Bloom et Sisask ont uni leurs forces en 2014 et, en 2016, ils ont décidé qu'ils étaient proches d'une solution. Bloom a même annoncé cela dans sa conférence, et seulement après cela, il a découvert que certaines des solutions de contournement qu'ils avaient trouvées se sont avérées erronées. Le couple a continué à travailler, plongeant dans la méthode de Bateman et Katz, et a finalement réalisé quelles nouvelles idées leur permettraient de transférer cette méthode du monde de Seth au monde des nombres entiers.
Le nouveau travail semble être correct sous tous les angles, a déclaré Katz. "Je ne croyais pas à leurs déclarations précédentes, mais je le crois."
Le travail de Bloom et Sisask est "une formidable réussite", a déclaré Fox. Eux et d'autres mathématiciens sont impatients de savoir si les techniques des nouveaux travaux s'appliquent à d'autres problèmes. «Je pense que ces méthodes auront un impact énorme sur les mathématiques», a déclaré Fox.
Quant à l'hypothèse d'Erds dans son ensemble, les travaux sont encore loin d'être achevés. Bloom et Sisask ont prouvé cette hypothèse uniquement pour des triplets de nombres également espacés, mais pas pour des progressions arithmétiques plus longues - cette tâche est encore hors de portée.
Et même la question des trois, que Bloom et Sisask ont déjà close, de l'avis de nombreux mathématiciens, n'aide pas particulièrement. Aussi difficile qu'il soit de prouver que la densité d'Erds garantit des triplets équidistants de nombres, les mathématiciens soupçonnent que la densité réelle à laquelle cette garantie cesse de fonctionner est bien inférieure - peut-être légèrement supérieure à la densité des ensembles conçus par Berend.
«Cela ne veut pas dire que nous avons complètement résolu ce problème, - a déclaré Bloom. "Nous avons éclairé un peu plus sur elle."
Bloom et Sisask ont probablement tiré le meilleur parti des méthodes actuelles, a déclaré Fox. «Il devrait y avoir des outils complètement nouveaux qui nous permettront d'aller beaucoup plus loin et d'obtenir un résultat nettement meilleur», a-t-il déclaré. Cependant, "ce n'est probablement pas la fin de l'histoire".