Pour comprendre comment les index B-tree sont nés, imaginons un monde sans eux et essayons de résoudre un problème typique. En cours de route, nous discuterons des problèmes auxquels nous serons confrontés et des moyens de les résoudre.

introduction
Dans le monde des bases de données, il existe deux manières les plus courantes de stocker des informations:
- Basé sur des structures basées sur le journal.
- Basé sur les pages.
L'avantage de la première méthode est qu'elle vous permet de lire et d'enregistrer facilement et rapidement des données. Les nouvelles informations ne peuvent être écrites qu'à la fin du fichier (enregistrement séquentiel), ce qui garantit une vitesse d'enregistrement élevée. Cette méthode est utilisée par des bases telles que Leveldb, Rocksdb, Cassandra.
La deuxième méthode (basée sur la page) divise les données en blocs de taille fixe et les enregistre sur le disque. Ces parties sont appelées "pages" ou "blocs". Ils contiennent des enregistrements (lignes, tuples) de tables.
Cette méthode de stockage de données est utilisée par MySQL, PostgreSQL, Oracle et autres. Et puisque nous parlons d'index dans MySQL, c'est exactement l'approche que nous allons considérer.
Stockage de données dans MySQL
Ainsi, toutes les données de MySQL sont enregistrées sur le disque sous forme de pages. La taille de la page est régulée par les paramètres de la base de données et est de 16 Ko par défaut.
Chaque page contient 38 octets d'en-têtes et une fin de 8 octets (comme indiqué sur la figure). Et l'espace alloué pour le stockage des données n'est pas complètement rempli, car MySQL laisse un espace vide sur chaque page pour les modifications futures.
Plus loin dans les calculs, nous négligerons les informations de service, en supposant que les 16 Ko de la page sont remplis de nos données. Nous n'entrerons pas dans l'organisation des pages InnoDB, c'est un sujet pour un article séparé. Vous pouvez en savoir plus ici .

Puisque nous avons convenu plus haut que les index n'existent pas encore, par exemple, nous allons créer une table simple sans aucun index (en fait, MySQL créera toujours un index, mais nous ne le prendrons pas en compte dans les calculs):
CREATE TABLE `product` (
`id` INT NOT NULL AUTO_INCREMENT,
`name` CHAR(100) CHARACTER SET utf8 COLLATE utf8_general_ci NOT NULL,
`category_id` INT NOT NULL,
`price` INT NOT NULL,
) ENGINE=InnoDB;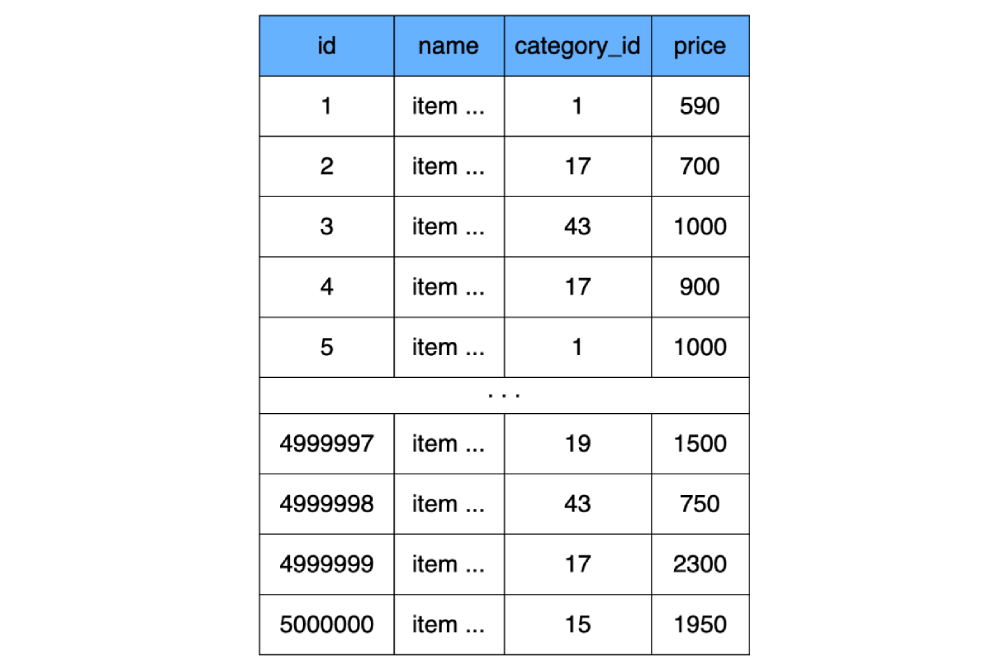
et exécutez la requête suivante:
SELECT * FROM product WHERE price = 1950;MySQL ouvrira le fichier dans lequel les données de la table sont stockées
productet commencera à parcourir tous les enregistrements (lignes) à la recherche de ceux requis, en comparant le champ pricede chaque ligne trouvée avec la valeur de la requête. Pour plus de clarté, je considère spécifiquement l'option avec une analyse complète du fichier, donc les cas où MySQL reçoit des données du cache ne nous conviennent pas.
À quels problèmes pouvons-nous faire face?
Disque dur
Puisque tout est stocké sur un disque dur, jetons un coup d'œil à son appareil. Le disque dur lit et écrit les données par secteurs (blocs). La taille d'un tel secteur peut aller de 512 octets à 8 Ko (selon le disque). Plusieurs secteurs consécutifs peuvent être combinés en grappes.
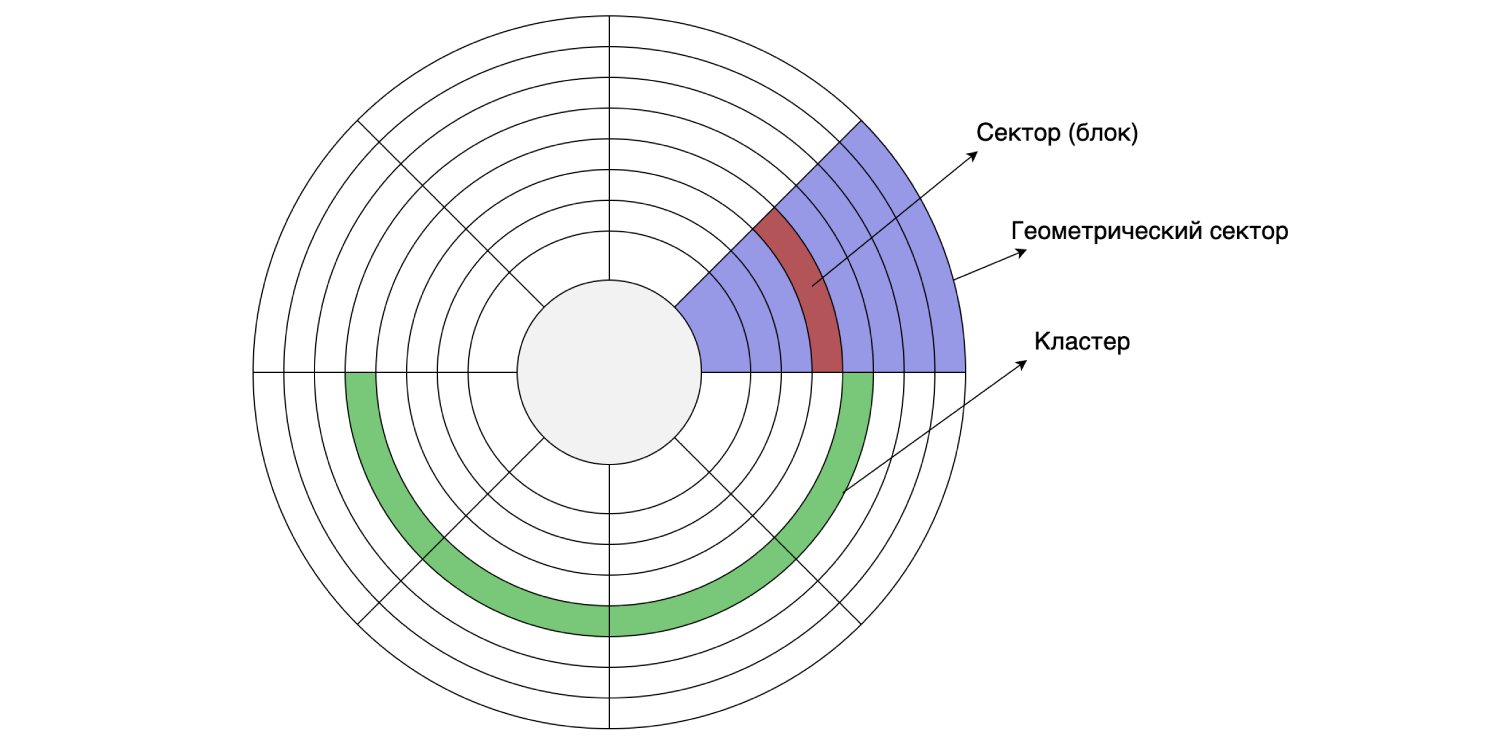
La taille du cluster peut être définie lors du formatage / partitionnement du disque, c'est-à-dire qu'elle est effectuée par programme. Supposons que la taille du secteur de disque soit de 4 Ko et que le système de fichiers soit partitionné avec une taille de cluster de 16 Ko: un cluster se compose de quatre secteurs. Comme nous nous en souvenons, MySQL stocke par défaut les données sur le disque dans des pages de 16 Ko, donc une page tient dans un cluster de disques.
Calculons l'espace que prendra notre plaque de produits, en supposant qu'elle contienne 500 000 articles. Nous avons trois champs de quatre octets
id, priceet category_id. Convenons que le champ de nom pour tous les enregistrements est rempli jusqu'à la fin (tous les 100 caractères), et chaque caractère prend 3 octets. (3 * 4) + (100 * 3) = 312 octets - c'est le poids d'une ligne de notre table, et en multipliant cela par 500000 lignes, nous obtenons le poids de la table de product156 mégaoctets.
Ainsi, pour stocker cette étiquette, 9750 clusters sont nécessaires sur le disque dur (9750 pages de 16 Ko).
Lors de l'enregistrement sur le disque, des clusters libres sont pris, ce qui conduit à un «étalement» des clusters d'une plaque (fichier) sur tout le disque (c'est ce qu'on appelle la fragmentation). La lecture de tels blocs de mémoire situés au hasard sur le disque est appelée lecture aléatoire. Cette lecture est plus lente car vous devez déplacer la tête du disque dur plusieurs fois. Pour lire le fichier entier, nous devons sauter partout sur le disque pour obtenir les clusters requis.
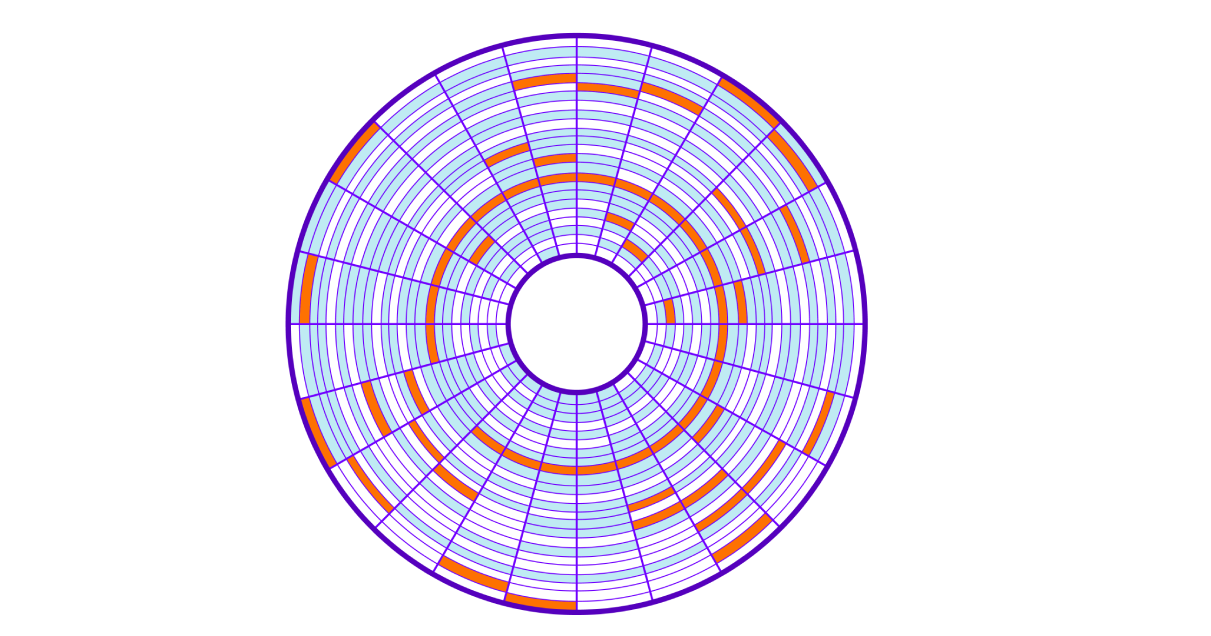
Revenons à notre requête SQL. Pour trouver toutes les lignes, le serveur devra lire tous les 9750 clusters dispersés sur le disque et il faudra beaucoup de temps pour déplacer la tête de lecture du disque. Plus nous utilisons nos données de clusters, plus la recherche sera lente. Et en plus, notre opération obstruera le système d'E / S du système d'exploitation.
En fin de compte, nous obtenons une vitesse de lecture faible; "Suspendre" le système d'exploitation, obstruant le système d'E / S; et effectuez de nombreuses comparaisons en vérifiant les conditions de requête pour chaque ligne.
Mon propre vélo
Comment pouvons-nous résoudre ce problème nous-mêmes?
Nous devons trouver comment améliorer les recherches dans les tables
product. Créons une autre table dans laquelle nous ne stockerons que le champ priceet le lien vers l'enregistrement (zone sur disque) dans notre table product. Prenons immédiatement comme règle que lors de l'ajout de données à une nouvelle table, nous stockerons les prix sous une forme triée.
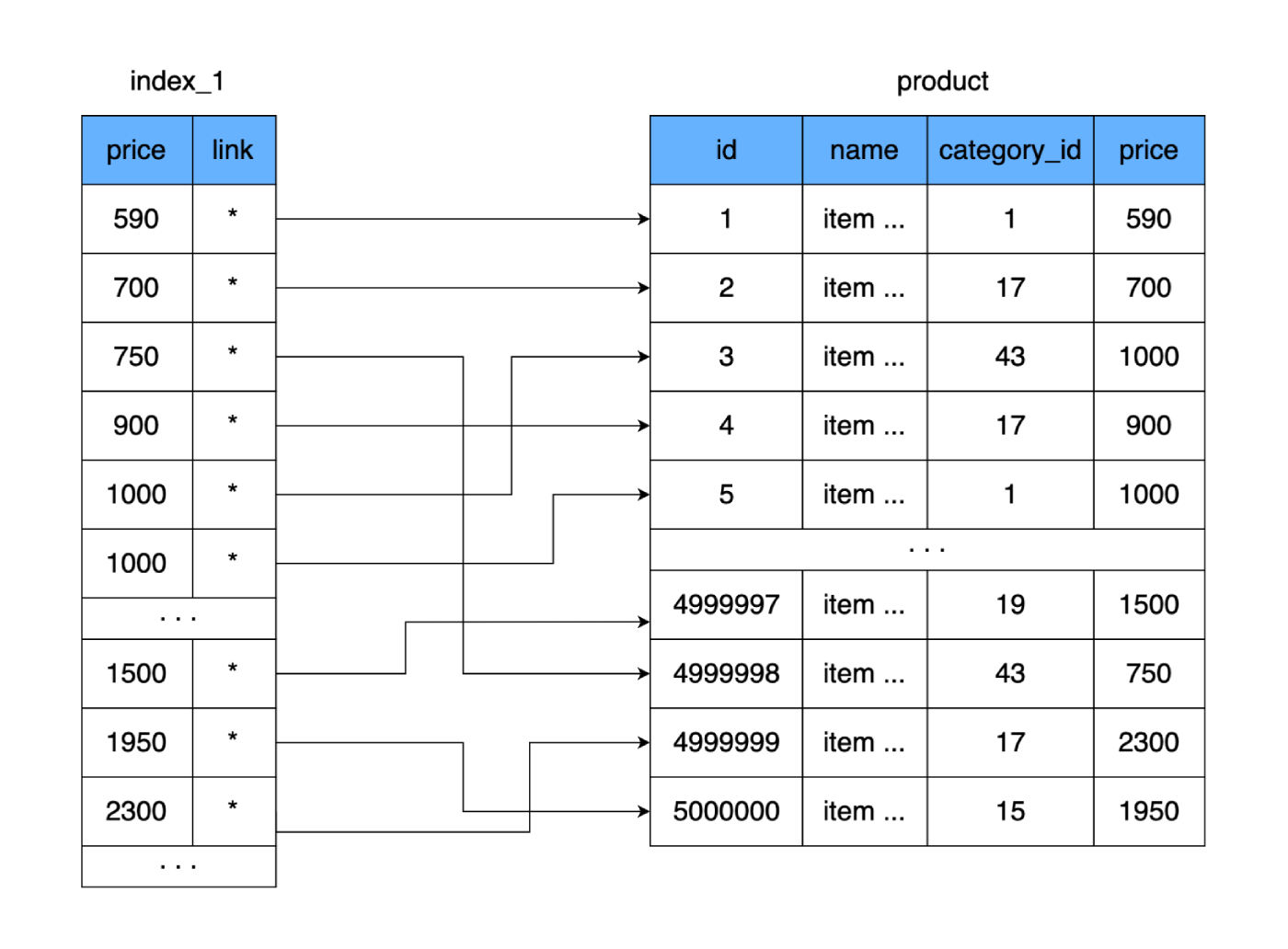
Qu'est-ce que ça nous donne? La nouvelle table, comme la principale, est stockée sur le disque page par page (en blocs). Il contient le prix et un lien vers la table principale. Calculons l'espace qu'une telle table prendra. Le prix prend 4 octets et laisse la référence à la table principale (adresse) sur 4 octets également. Pour 500 000 lignes, notre nouvelle table ne pèsera que 4 Mo. De cette façon, beaucoup plus de lignes du nouveau tableau tiendront sur une page de données, et moins de pages seront nécessaires pour stocker tous nos prix.
Si une table complète nécessite 9 750 clusters de disques durs (ou dans le pire des cas, 9 750 sauts de disque dur), la nouvelle table ne peut contenir que 250 clusters. Cela réduira considérablement le nombre de clusters utilisés sur le disque, et donc le temps consacré aux lectures aléatoires. Même si nous lisons toute notre nouvelle table et comparons les valeurs pour trouver le bon prix, dans le pire des cas, il faudra 250 sauts à travers les grappes de la nouvelle table. Et après avoir trouvé l'adresse requise, nous lirons un autre cluster où se trouvent les données complètes. Résultat: 251 lectures par rapport aux 9750 d'origine. La différence est significative.
De plus, pour rechercher une telle table, vous pouvez utiliser, par exemple, un algorithme de recherche binaire (puisque la liste est triée). Cela économisera encore plus sur le nombre de lectures et d'opérations de comparaison.
Appelons notre deuxième table un index.
Hourra! Nous avons créé notre propre index de
Mais arrêtez: au fur et à mesure que la table grandit, l'index deviendra de plus en plus gros, et nous reviendrons finalement au problème d'origine. La recherche prendra à nouveau du temps.
Un autre index
Et si vous créez un autre index en plus de celui existant?
Seulement cette fois, nous n'écrirons pas chaque valeur du champ
price, mais nous associerons une valeur à une page entière (bloc) de l'index. Autrement dit, un niveau d'index supplémentaire apparaîtra, qui pointera vers l'ensemble de données de l'index précédent (la page sur le disque où les données du premier index sont stockées).
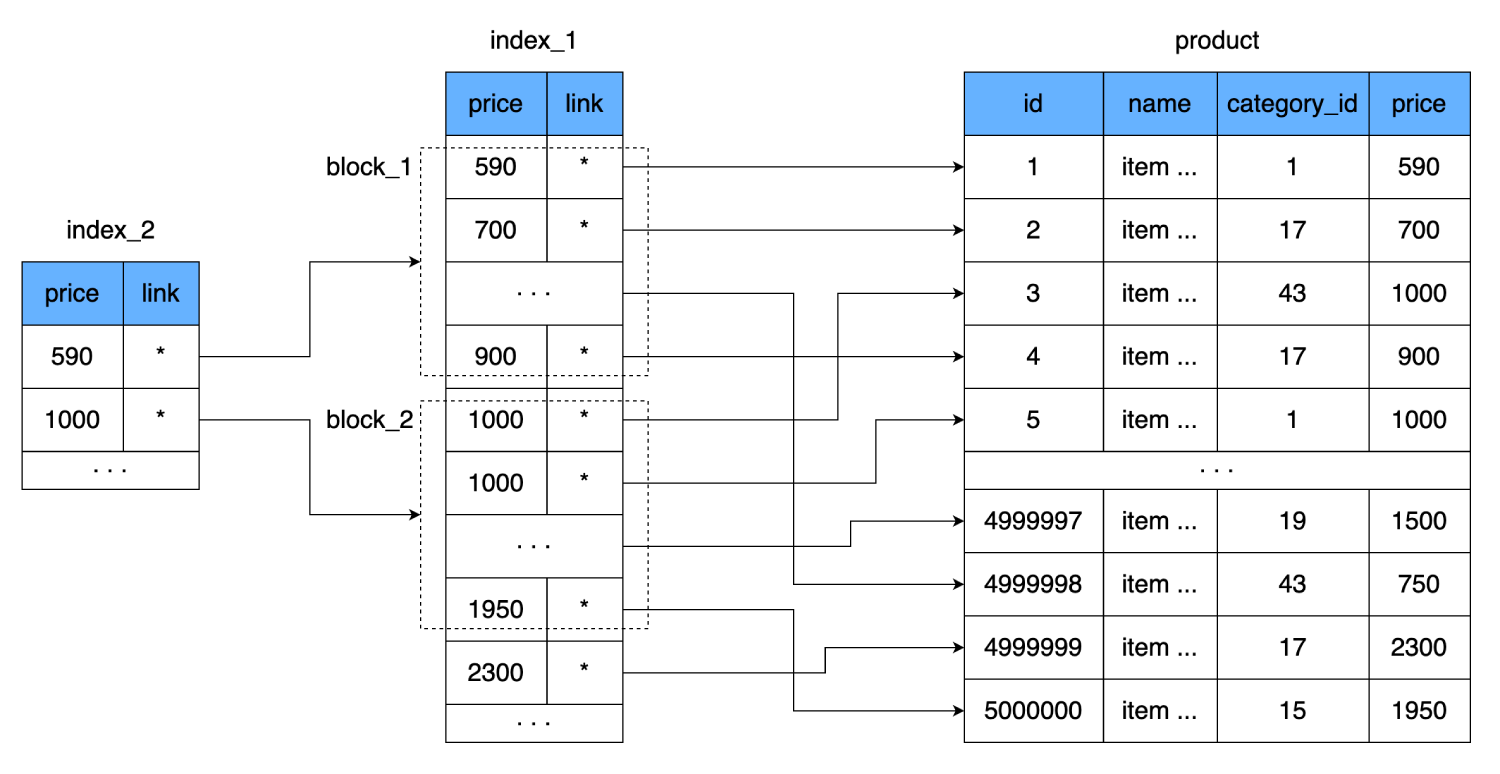
Cela réduira encore le nombre de lectures. Une ligne de notre index prend 8 octets, c'est-à-dire que nous pouvons contenir 2000 lignes de ce type sur une page de 16 kilo-octets. Le nouvel index contiendra un lien vers le bloc de 2000 lignes du premier indice et le prix à partir duquel ce bloc commence. Une de ces lignes prend également 8 octets, mais leur nombre est fortement réduit: au lieu de 500 000, seulement 250. Ils tiennent même dans un cluster de disques durs. Ainsi, afin de trouver le prix souhaité, nous pourrons déterminer exactement dans quel bloc de 2000 lignes il se trouve. Et dans le pire des cas, pour retrouver le même enregistrement, on:
- Faisons une lecture du nouvel index.
- Après avoir parcouru 250 lignes, nous trouvons un lien vers le bloc de données à partir du deuxième index.
- Considérez un cluster qui contient 2000 lignes avec des prix et des liens vers la table principale.
- Après avoir vérifié ces 2000 lignes, nous trouverons le saut requis et un autre saut de temps sur le disque pour lire le dernier bloc de données.
Nous obtiendrons un total de 3 sauts de cluster.
Mais ce niveau sera tôt ou tard également rempli de nombreuses données. Par conséquent, nous devrons répéter tout ce que nous avons fait, en ajoutant encore et encore un nouveau niveau. Autrement dit, nous avons besoin d'une structure de données pour stocker l'index, qui ajoutera de nouveaux niveaux à mesure que la taille de l'index augmente et équilibrera indépendamment les données entre eux.
Si nous retournons les tables pour que le dernier index soit en haut et que la table principale avec des données soit en bas, nous obtenons une structure très similaire à un arbre.
La structure de données B-tree fonctionne sur un principe similaire, elle a donc été choisie à ces fins.
B-Tree en bref
Les index les plus couramment utilisés dans MySQL sont les index ordonnés B-tree (arbre de recherche équilibré) .
L'idée générale d'un arbre B est similaire à nos tables d'index. Les valeurs sont stockées dans l'ordre et toutes les feuilles de l'arbre sont à la même distance de la racine.
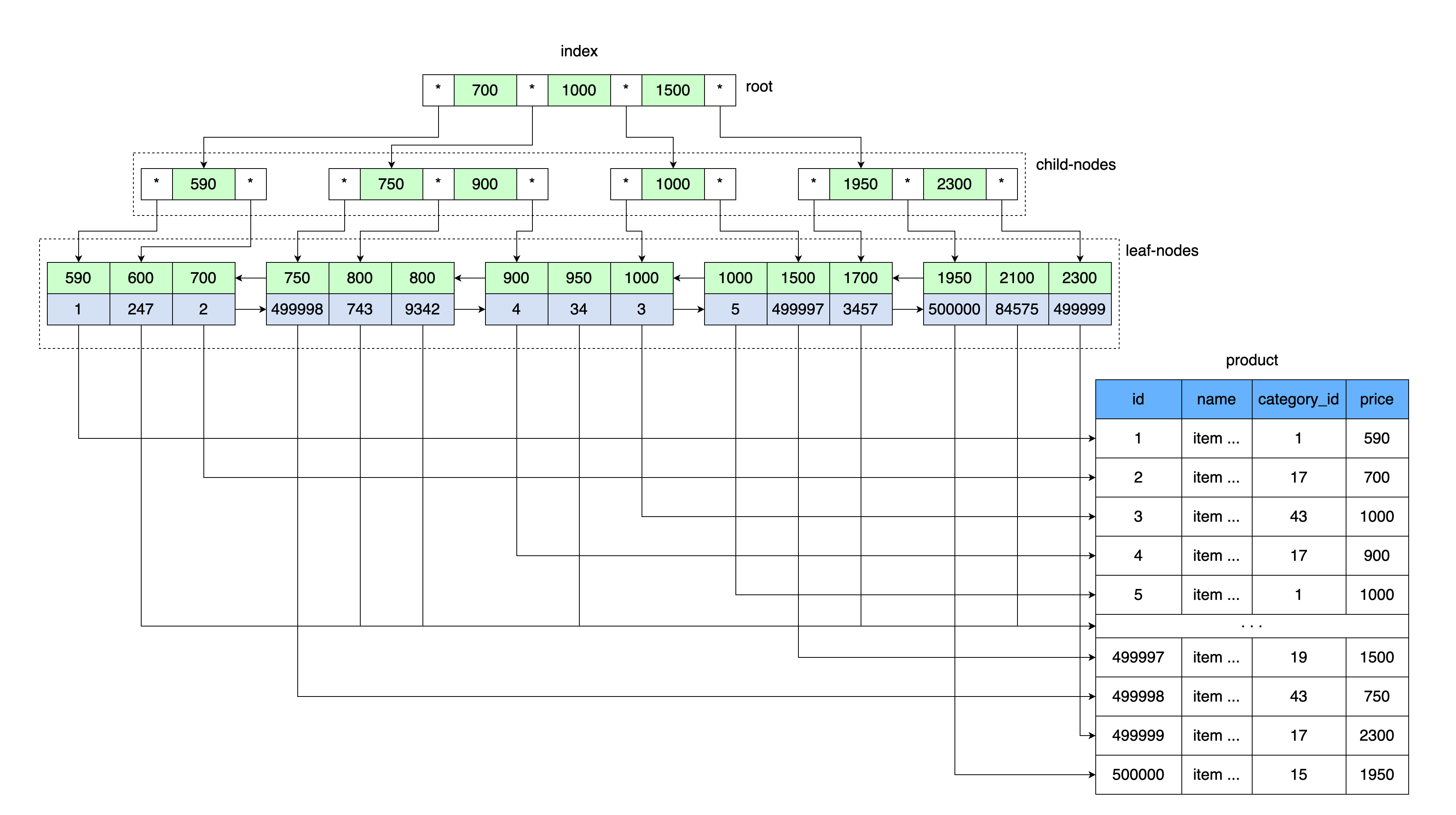
Tout comme notre table avec un index stockait une valeur de prix et un lien vers un bloc de données contenant une plage de valeurs avec ce prix, la racine de l'arbre B stocke une valeur de prix et un lien vers une zone de mémoire sur le disque.
Tout d'abord, la page qui contient la racine de l'arbre B est lue. En outre, après avoir entré la plage de clés, il y a un pointeur vers le nœud enfant souhaité. La page du nœud enfant est lue, à partir de laquelle le lien vers la feuille de données est tiré de la valeur de clé, et la page contenant les données est lue à partir de ce lien.
B-tree dans InnoDB
Plus spécifiquement, InnoDB utilise une structure de données arborescente B +.
Chaque fois que vous créez une table, vous créez automatiquement une arborescence B +, car MySQL stocke un tel index pour les clés primaires et secondaires.
Les clés secondaires stockent en outre les valeurs de la clé primaire (cluster) comme référence à la ligne de données. Par conséquent, la clé secondaire augmente de la taille de la valeur de la clé primaire.
De plus, les arborescences B + utilisent des liens supplémentaires entre les nœuds enfants, ce qui augmente la vitesse de recherche sur une plage de valeurs. En savoir plus sur la structure des index d'arborescence b + dans InnoDB ici .
Résumer
L'index b-tree offre un grand avantage lors de la recherche de données sur une plage de valeurs en raison d'une réduction multiple de la quantité d'informations lues à partir du disque. Il participe non seulement à la recherche par condition, mais également aux tris, jointures, regroupements. Découvrez comment MySQL utilise les index ici .
La plupart des requêtes adressées à la base de données ne sont que des requêtes visant à rechercher des informations par valeur ou par plage de valeurs. Par conséquent, dans MySQL, l'index le plus couramment utilisé est un index b-tree.
En outre, l'index b-tree aide lors de la récupération des données. Étant donné que la clé primaire (index clusterisé) et la valeur de la colonne sur laquelle l'index non cluster est construit (clé secondaire) sont stockées dans les feuilles d'index, vous ne pouvez plus accéder à la table principale pour ces données et les extraire de l'index. C'est ce qu'on appelle l'indice de couverture. Vous trouverez plus d'informations sur les index clusterisés et non clusterisés dans cet article .
Les index, comme les tables, sont également stockés sur disque et occupent de l'espace. Chaque fois que des informations sont ajoutées à la table, l'index doit être mis à jour pour contrôler l'exactitude de tous les liens entre les nœuds. Cela crée une surcharge dans l'écriture des informations, ce qui est le principal inconvénient des index b-tree. Nous sacrifions la vitesse d'écriture pour augmenter la vitesse de lecture.
- MySQL . 3-
: ,
: 2018 - blog.jcole.us/innodb
- dev.mysql.com/doc/refman/8.0/en/innodb-storage-engine.html