🧜🏿 🥡 👐🏾 Espaces vectoriels 🚉 🕘 👩🏽‍✈️

Lors de la recherche scientifique et appliquée, des modèles sont souvent créés dans lesquels des points et / ou vecteurs de certains espaces sont considérés. Par exemple, les modèles de chiffrement à courbe elliptique utilisent des espaces affines et projectifs. Ils recourent à des projectifs lorsqu'il faut accélérer les calculs, car dans les formules de manipulation des points d'une courbe elliptique dérivée dans le cadre de l'espace projectif, il n'y a pas d'opération de division par une coordonnée, qui ne peut être contournée dans le cas d'un espace affine .

L'opération de division n'est qu'une des opérations les plus «coûteuses». Le fait est que dans les champs algébriques, et par conséquent dans les groupes, il n'y a pas du tout d'opération de division, et la solution (quand il est impossible de ne pas diviser) est que l'opération de division est remplacée par la multiplication, mais multipliée non par la coordonnée elle-même, mais par sa valeur inverse ... Il s'ensuit que nous devons d'abord impliquer l'algorithme euclidien étendu GCD et autre chose. En bref, tout n'est pas aussi simple que celui décrit par les auteurs de la plupart des publications sur l'ECC. Presque tout ce qui a été publié sur ce sujet et pas seulement sur Internet m'est familier. Non seulement les auteurs ne sont pas compétents et se livrent à des grossièretés, mais les évaluateurs de ces publications ajoutent des auteurs dans les commentaires, c'est-à-dire qu'ils ne voient ni lacunes ni erreurs évidentes. À propos d'un article normal, ils écrivent que c'est déjà le 100500e et qu'il n'a aucun effet.Jusqu'ici tout est arrangé sur Habré, l'analyse des publications est énorme, mais pas la qualité du contenu. Il n'y a rien à objecter ici - la publicité est le moteur des affaires.

Espace vectoriel linéaire

L'étude et la description des phénomènes du monde environnant nous conduisent nécessairement à l'introduction et à l'utilisation d'un certain nombre de concepts tels que les points, les nombres, les espaces, les droites, les plans, les repères, les vecteurs, les ensembles, etc.

Soit r _<3>= <r1, r2, r3> vecteur de l'espace tridimensionnel, spécifie la position d'une particule (point) par rapport à l'origine. Si nous considérons N éléments, alors la description de leur position nécessite de spécifier 3 ∙ N coordonnées, qui peuvent être considérées comme les coordonnées d'un vecteur dans un espace à 3N dimensions. Si nous considérons les fonctions continues et leurs collections, alors nous arrivons à des espaces dont la dimension est égale à l'infini. En pratique, ils se limitent souvent à n'utiliser que le sous-espace d'un tel espace de fonction de coordonnées de dimension infinie qui a un nombre fini de dimensions.

Exemple 1 . La série de Fourier est un exemple d'utilisation de l'espace fonctionnel. Considérons l'expansion d'une fonction arbitraire dans une série de Fourier

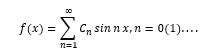
Il peut être interprété comme l'expansion du "vecteur" f (x) en un ensemble infini de vecteurs de base "orthogonaux" sinnx

C'est un exemple d'abstraction et d'extension du concept de vecteur à un nombre infini de dimensions. En effet, on sait que pour -π≤x≤π

L'essence d'un examen plus approfondi ne souffrira pas si nous faisons abstraction de la dimension de l'espace vectoriel abstrait - que ce soit 3, 3N ou l'infini, bien que pour des applications pratiques, les champs de dimension finie et les espaces vectoriels soient d'un plus grand intérêt.

Un ensemble de vecteurs r1, r2,… sera appelé un espace vectoriel linéaire L si la somme de deux de ses éléments est également dans cet ensemble et si le résultat de la multiplication d'un élément par un nombre C est également inclus dans cet ensemble. Faisons une réserve tout de suite que les valeurs du nombre C peuvent être sélectionnées à partir d'un ensemble de nombres bien défini F - le champ de résidus modulo un nombre premier p, qui est considéré comme attaché à

L.Exemple 2 . Un ensemble de 8 vecteurs composé de n = nombres binaires de 5 bits

r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 forme l'espace vectoriel L si les nombres C є {0,1}. Ce petit exemple permet de vérifier la manifestation des propriétés d'un espace vectoriel inclus dans sa définition.

La sommation de ces vecteurs est effectuée modulo deux au niveau du bit, c'est-à-dire sans transférer ceux vers le bit le plus significatif. Notez que si tous les C sont réels (dans le cas général C appartiennent au domaine des nombres complexes), alors l'espace vectoriel est appelé réel.

Formellement, les axiomes de l'espace vectoriel s'écrit comme suit:

r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L - commutativité et fermeté d'addition;

(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 - associativité d'addition;

ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L - existence d'un élément neutre;

ri + (- ri) = r0, pour ∀i il existe un vecteur opposé (-ri) є L;

1 ∙ ri = ri ∙ 1 = ri existence d'une unité de multiplication;

α (β ∙ ri) = (α ∙ β) ∙ ri; α, β, 1, 0 sont des éléments du champ numérique F, ri є L; la multiplication par les scalaires est associative; le résultat de la multiplication appartient à L;

(α + β) ri = α ∙ ri + β ∙ ri; pour ∀i, ri є L, α, β sont des scalaires;

a (ri + rj) = ari + arj pour tout a, ri, rj є L;

a ∙ 0 = 0, 0 ∙ ri = 0; (-1) ∙ ri = - ri.

Dimension et base de l'espace vectoriel

Lors de l'étude des espaces vectoriels, il est intéressant de clarifier des questions telles que le nombre de vecteurs formant l'espace entier; quelle est la dimension de l'espace; quel est le plus petit ensemble de vecteurs, en lui appliquant l'opération de sommation et de multiplication par un nombre, permet de former tous les vecteurs de l'espace? Ces questions sont fondamentales et ne peuvent être ignorées, car sans réponse, la clarté de perception de tout ce qui constitue la théorie des espaces vectoriels est perdue.

Il s'est avéré que la dimension de l'espace est étroitement liée à la dépendance linéaire des vecteurs, et au nombre de vecteurs linéairement indépendants qui peuvent être choisis dans l'espace étudié de plusieurs manières.

Indépendance linéaire des vecteurs

Un ensemble de vecteurs r1, r2, r3 ... r de L est dit linéairement indépendant si pour eux la relation

n'est remplie que sous la condition d'égalité simultanée

с_{1} = с_{2} = \dots = с_{р} = 0

$_1=_2=…=_=0$ ...

Tout

с_{k}

$_k$ , k = 1 (1) p, appartiennent au champ numérique des résidus modulo deux

F = {0, 1}.

Si dans un espace vectoriel L on peut choisir un ensemble de p vecteurs pour lesquels la relation

c_{1} r_{1} + c_{2} r_{2} + . . . + c_{p} r_{p} = 0

$c_1 r_1+c_2 r_2+...+c_p r_p=0$ est exécuté, à condition que tous

с_{k} = 0

$_k = 0$ simultanément, i.e. il s'est avéré possible de sélectionner l'ensemble

с_{k}

$_k$ , k = 1 (1) , parmi lesquels il y a des non nuls, alors de tels vecteurs

r_{i}

$r_i$ sont appelés linéairement dépendants.

Exemple 3 . Deux vecteurs dans l'avion

е_{1}

$_1$ = <0, 1> ^T et

е_{2}

$_2$ = <1, 0> ^T sont linéairement indépendants, puisque dans la relation (T-transposition)

il est impossible de trouver une paire de nombres

с_{1}, с_{2}

$_1, _2$ coefficients non égaux à zéro en même temps, de sorte que le rapport est respecté.

Trois vecteurs

е_{1}

$_1$ = <0, 1> ^T ,

е_{2}

$_2$ = <1, 0> ^T ,

е_{3}

$_3$ = <1, 1> ^T forment un système de vecteurs linéairement dépendants, puisque dans la relation

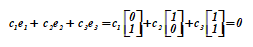
l'égalité peut être assurée en choisissant les coefficients

с_{1} = с_{2} = 1, с_{3} = - 1

$_1 = _2 = 1, _3 = –1$ pas égal à zéro en même temps. De plus, le vecteur

e_{3} = е_{1} + е_{2}

$e_3 = _1 + _2$ est une fonction

е_{1}

$_1$ et

е_{2}

$_2$ (leur somme), qui indique la dépendance

e_{3}

$e_3$ de

е_{1}

$_1$ et

е_{2}

$_2$ ... La preuve du cas général est la suivante.

Laissez au moins une des valeurs

с_{k}

$_k$ , k = 1 (1) p, par exemple,

с_{р} \neq 0

$_ ≠ 0$ , et la relation est satisfaite. Cela signifie que les vecteurs

r_{k}

$r_k$ , k = 1 (1) , sont linéairement dépendants

Séparons explicitement le vecteur r

On dit que le vecteur r _p est une combinaison linéaire de vecteurs

r_{1}, r_{2} \dots r_{р} - 1

$r_1, r_2… r_-1$ ou r _{p à} travers les vecteurs restants est exprimé de manière linéaire, c'est-à-dire r _p dépend linéairement des autres. Il est leur fonction.

Sur un plan bidimensionnel, trois vecteurs quelconques sont linéairement dépendants, mais deux vecteurs non colinéaires quelconques sont indépendants. Dans l'espace 3D, trois vecteurs non coplanaires quelconques sont linéairement indépendants, mais quatre vecteurs quelconques sont toujours linéairement dépendants.

Dépendance / indépendance de la population {

e_{1}, e_{2}, e_{3}, . . ., e_{n}

${e_1, e_2, e_3, ..., e_n}$ } les vecteurs sont souvent déterminés en calculant le déterminant de la matrice de Gram (ses lignes sont les produits scalaires de nos vecteurs). Si le déterminant est nul, il existe des vecteurs dépendants parmi les vecteurs; si le déterminant est différent de zéro, les vecteurs de la matrice sont indépendants.

Le déterminant de Gram (Gramian) du système vectoriel

e_{1}, e_{2}, \dots, e_{n} e_{1}, e_{2}, \dots, e_{n}

${\displaystyle \mathbf {e} _{1},\;\mathbf {e} _{2},\;\ldots ,\mathbf {e} _{n}}\mathbf{e}_1,\;\mathbf{e}_2,\;\ldots,\mathbf{e}_n$

le déterminant de la matrice de Gram de ce système est appelé dans l'espace euclidien:

| \begin{matrix} ⟨ e_{1}, e_{1} ⟩ & ⟨ e_{1}, e_{2} ⟩ & \dots & ⟨ e_{1}, e_{n} ⟩ \\ ⟨ e_{2}, e_{1} ⟩ & ⟨ e_{2}, e_{2} ⟩ & \dots & ⟨ e_{2}, e_{n} ⟩ \\ \dots & \dots & \dots & \dots \\ ⟨ e_{n}, e_{1} ⟩ & ⟨ e_{n}, e_{2} ⟩ & \dots & ⟨ e_{n}, e_{n} ⟩ \end{matrix} |, | \begin{matrix} ⟨ e_{1}, e_{1} ⟩ & ⟨ e_{1}, e_{2} ⟩ & \dots & ⟨ e_{1}, e_{n} ⟩ \\ ⟨ e_{2}, e_{1} ⟩ & ⟨ e_{2}, e_{2} ⟩ & \dots & ⟨ e_{2}, e_{n} ⟩ \\ \dots & \dots & \dots & \dots \\ ⟨ e_{n}, e_{1} ⟩ & ⟨ e_{n}, e_{2} ⟩ & \dots & ⟨ e_{n}, e_{n} ⟩ \end{matrix} |,

${\displaystyle {\begin{vmatrix}\langle e_{1},\;e_{1}\rangle &\langle e_{1},\;e_{2}\rangle &\ldots &\langle e_{1},\;e_{n}\rangle \\\langle e_{2},\;e_{1}\rangle &\langle e_{2},\;e_{2}\rangle &\ldots &\langle e_{2},\;e_{n}\rangle \\\ldots &\ldots &\ldots &\ldots \\\langle e_{n},\;e_{1}\rangle &\langle e_{n},\;e_{2}\rangle &\ldots &\langle e_{n},\;e_{n}\rangle \\\end{vmatrix}},}\begin{vmatrix} \langle e_1,\;e_1\rangle & \langle e_1,\;e_2\rangle & \ldots & \langle e_1,\;e_n\rangle \\ \langle e_2,\;e_1\rangle & \langle e_2,\;e_2\rangle & \ldots & \langle e_2,\;e_n\rangle \\ \ldots & \ldots & \ldots & \ldots \\ \langle e_n,\;e_1\rangle & \langle e_n,\;e_2\rangle & \ldots & \langle e_n,\;e_n\rangle \\ \end{vmatrix},$

Où

⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩ ⟨ e_{i}, e_{j} ⟩

${\displaystyle \langle e_{i},\;e_{j}\rangle }\langle e_i,\;e_j\rangle{\displaystyle \langle e_{i},\;e_{j}\rangle }\langle e_i,\;e_j\rangle$ - produit scalaire des vecteurs

e_{i} e_{i}

${\displaystyle \mathbf {e} _{i}}\mathbf{e}_i$ et

e_{j} e_{j}

${\displaystyle \mathbf {e} _{j}}\mathbf{e}_j$ ...

Dimension et base d'un espace vectoriel

La dimension s = d (L) d'un espace L est définie comme le plus grand nombre de vecteurs dans L formant un ensemble linéairement indépendant. La dimension n'est pas le nombre de vecteurs dans L, qui peut être infini, ni le nombre de composantes vectorielles.

Les espaces de dimension finie s ≠ ∞ sont dits de dimension finie si

s = ∞, de dimension infinie.

La réponse à la question sur le nombre minimum et la composition des vecteurs qui assurent la génération de tous les vecteurs dans un espace vectoriel linéaire est la déclaration suivante.

Toute collection de s de vecteurs linéairement indépendants dans l'espace L forme ses bases et s. Cela découle du fait que tout vecteur

r_{k}

$r_k$ L'espace vectoriel linéaire s-dimensionnel L peut être représenté d'une manière unique comme une combinaison linéaire de vecteurs de base.

Nous fixons et désignons par le symbole

е_{i}

$_i$ , i = 1 (1) s, est l'un des n-uplets formant la base de l'espace L. Alors

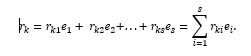
Les nombres r _ki , i = 1 (1) s sont appelés les coordonnées du vecteur

r_{k}

$r_k$ dans la base

е_{i}

$_i$ , i = 1 (1) s, et r _ki = (

е_{i}

$_i$ ,

r_{k}

$r_k$ ).

Montrons l'unicité de la représentation

r_{k}

$r_k$ ... De toute évidence, l'ensemble

e_{1}, e_{2}, . . ., e_{s}

$e_1,e_2,...,e_s$ ,

r_{k}

$r_k$ dépend, puisque

е_{i}

$_i$ , i = 1 (1) s est une base. En d'autres termes, il existe de tels

с_{1}, с_{2} . . . с_{s}, c_{k}

$_1, _2... _s, c_k$ pas simultanément égal à zéro, que

c_{1} \cdot e_{1} + c_{2} \cdot e_{2} + . . . + c_{s} \cdot e_{s} + c_{k} \cdot r_{k} = 0

$c_1·e_1 + c_2·e_2 + ...+ c_s·e_s + c_k·r_k = 0$ ...

De plus, laissez

c_{k} \neq 0

$c_k ≠ 0$ parce que si

c_{k} = 0

$c_k = 0$ , puis au moins un des

с_{1}, с_{2}, . . ., с_{s}

$_1, _2 , ... , _s$ , ce serait différent de zéro puis vecteurs

e_{i}

$e_i$ , i = 1 (1) s, serait linéairement dépendant, ce qui est impossible, car c'est une base. Par conséquent,

En supposant

, nous aurons

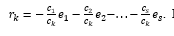
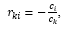
En utilisant la méthode de preuve "par contradiction", nous supposons que la représentation écrite

r_{k}

$r_k$ pas le seul dans cette base et il y a autre chose

Ensuite, nous écrivons la différence des représentations, qui, bien sûr, est exprimée comme étant

évidemment, les côtés droit et gauche sont égaux, mais le côté gauche représente la différence du vecteur avec lui-même, c'est-à-dire qu'il est égal à zéro. Par conséquent, le côté droit est également nul. Vecteurs

е_{i}

$_i$ , i = 1 (1) s sont linéairement indépendants, donc tous les coefficients pour eux ne peuvent être que zéro. De cela, nous obtenons cela

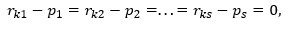
et cela n'est possible que pour

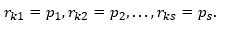
Le choix de la base. Orthonormalité

Les vecteurs sont appelés normalisés si la longueur de chacun d'eux est égale à un. Ceci peut être réalisé en appliquant la procédure de normalisation à des vecteurs arbitraires.

Les vecteurs sont appelés orthogonaux s'ils sont perpendiculaires les uns aux autres. De tels vecteurs peuvent être obtenus en appliquant une procédure d'orthogonalisation à chacun d'eux. Si les deux propriétés sont satisfaites pour un ensemble de vecteurs, alors les vecteurs sont appelés orthonormés.

La nécessité de prendre en compte les bases orthonormées est causée par la nécessité d'utiliser des transformations rapides des fonctions unidimensionnelles et multidimensionnelles. Les tâches d'un tel traitement se posent dans l'étude des codes codant des messages d'information dans les réseaux de communication à des fins diverses, dans l'étude des images obtenues

grâce à des dispositifs automatiques et automatisés, dans un certain nombre d'autres domaines utilisant des représentations numériques de l'information.

Définition. La collection de n vecteurs linéairement indépendants d'un

espace vectoriel V à n dimensions est appelée sa base.

Théorème . Chaque vecteur x d'un espace vectoriel linéaire à n dimensions V peut être représenté, par ailleurs, de manière unique, sous la forme d'une combinaison linéaire de vecteurs de base. L'espace vectoriel V sur le champ F a les propriétés suivantes:

0 x = 0 (0 sur le côté gauche de l'égalité est un élément neutre du groupe additif du champ F; 0 sur le côté droit de l'égalité est un élément de l'espace V, qui est un élément unitaire neutre du groupe additif V, appelé vecteur zéro );

(- 1) · x = –x; –1є F; x є V; –X є V;

Si α x = 0єV, alors pour x ≠ 0 toujours α = 0.

Soit Vn (F) l'ensemble de toutes les suites (x1, x2, ..., xn) de longueur n avec des composantes du champ F, c'est-à-dire, Vn (F) = {x, tel que x = (x1, x2, ..., xn), xi є F;

i = 1 (1) n}.

L'addition et la multiplication par un scalaire sont définies comme suit:

x + y = (x1 + y1, x2 + y2,…, xn + yn);

α x = (α x1, α x2,…, α xn), où y = (y1, y2,…, yn),

alors Vn (F) est un espace vectoriel sur le champ F.

Exemple 4 . Dans l'espace vectoriel r® = 00000, r1 = 10101, r2 = 11010, r3 = 10101 sur le champ F2 = {0,1} déterminer sa dimension et sa base.

Décision. Formons un tableau d'addition de vecteurs d'un espace vectoriel linéaire

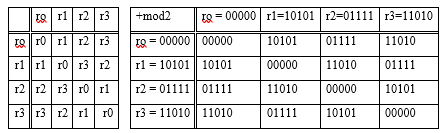
Dans cet espace vectoriel V = {ro, r1, r2, r3} chaque vecteur a lui-même pour opposé. Deux vecteurs quelconques, à l'exclusion de r®, sont linéairement indépendants, ce qui est facile à vérifier

c1 · r1 + c2 · r2 = 0; c1 r1 + c3 r3 = 0; c2 r2 + c3 r3 = 0;

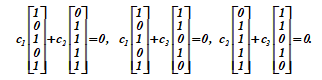
Chacune des trois relations n'est valable que pour les valeurs nulles simultanées des paires de coefficients ci, cj є {0,1}.

Lorsque trois vecteurs différents de zéro sont considérés simultanément, l'un d'eux est toujours la somme des deux autres ou est égal à lui-même, et r1 + r2 + r3 = r.

Ainsi, la dimension de l'espace vectoriel linéaire considéré est égale à deux s = 2, d (L) = s = 2, bien que chacun des vecteurs ait cinq composantes. La base de l'espace est la collection (r1, r2). Vous pouvez utiliser la paire (r1, r3) comme base.

Théoriquement et pratiquement, la question de la description de l'espace vectoriel est importante. Il s'avère que tout ensemble de vecteurs de base peut être vu comme des lignes d'une certaine matrice G, appelée matrice génératrice de l'espace vectoriel. Tout vecteur de cet espace peut être représenté comme une combinaison linéaire de lignes de la matrice G ( comme par exemple ici ).

Si la dimension de l'espace vectoriel est égale à k et est égale au nombre de lignes de la matrice G, le rang de la matrice G, alors il y a évidemment k coefficients avec q valeurs différentes pour générer toutes les combinaisons linéaires possibles de lignes de matrice. De plus, l'espace vectoriel L contient q ^k vecteurs.

L'ensemble de tous les vecteurs de ℤpn avec des opérations d'addition de vecteurs et de multiplication d'un vecteur par un scalaire de ℤp est un espace vectoriel linéaire.

Définition . Un sous-ensemble W d'un espace vectoriel V satisfaisant les conditions:

Si w1, w2 є W, alors w1 + w2 є W,

Pour tout α є F et w є W, l'élément αw є W est

lui - même un espace vectoriel sur le champ F et est appelé un sous-espace de l'espace vectoriel V.

Soit V un espace vectoriel sur un corps F et un ensemble W ⊆ V. Un ensemble W est un sous-espace de V si W par rapport aux opérations linéaires définies dans V est un espace vectoriel linéaire.

Table. Caractéristiques des espaces vectoriels

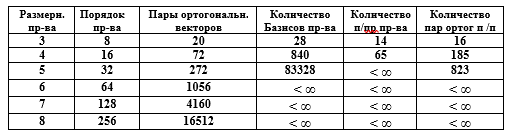
La compacité de la représentation matricielle d'un espace vectoriel est évidente. Par exemple, la spécification de L vecteurs de nombres binaires de 50 bits, parmi lesquels 30 vecteurs forment la base de l'espace vectoriel, nécessite la formation de la matrice G [30,50], et le nombre de vecteurs décrit dépasse 10 ⁹ , ce qui semble déraisonnable dans la notation élément par élément.

Toutes les bases de tout espace L sont divisées par le sous-groupe P des matrices non dégénérées avec det G> 0 en deux classes. L'une d'elles (arbitrairement) est appelée une classe avec des bases orientées positivement (celles de droite), l'autre classe contient des bases de gauche.

Dans ce cas, ils disent qu'une orientation est donnée dans l'espace. Après cela, toute base est un ensemble ordonné de vecteurs.

Si la numérotation de deux vecteurs est modifiée dans la base droite, la base deviendra gauche. Cela est dû au fait que deux lignes de la matrice G sont permutées, par conséquent, le déterminant detG changera de signe.

Norme et produit scalaire des vecteurs

Après avoir résolu les questions sur la recherche de la base d'un espace vectoriel linéaire, sur la génération de tous les éléments de cet espace et sur la représentation de tout élément et de l'espace vectoriel lui-même à travers les vecteurs de base, nous pouvons poser le problème de la mesure dans cet espace des distances entre éléments, angles entre vecteurs, valeurs des composantes vectorielles , les longueurs des vecteurs eux-mêmes.

Un espace vectoriel réel ou complexe L est appelé un espace vectoriel normé si chaque vecteur r qu'il contient peut être associé à un nombre réel || r || - module vectoriel, norme. Un vecteur unitaire est un vecteur dont la norme est égale à un. Le vecteur zéro a zéro composante.

Définition... Un espace vectoriel est dit unitaire si une opération binaire y est définie qui assigne un scalaire à chaque paire ri, rj de vecteurs de L. Entre parenthèses (ri, rj) le produit scalaire ou interne de ri et rj est écrit (noté), et

1. (ri, rj) = ri ∙ rj;

2. (ri, rj) = (ri ∙ rj) *, où * indique une conjugaison complexe ou une symétrie hermitienne;

3. (ri, rj) = (ri ∙ rj) - loi associative;

4. (ri + rj, rk) = (ri ∙ rk) + (rj ∙ rk) - loi distributive;

5. (ri, rk) ≥ 0 et de (ri, rj) = 0 il suit ri = 0.

Définition . La valeur positive de la racine carrée

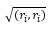est appelée la norme (ou longueur, module) du vecteur ri. Si

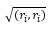= 1, alors le vecteur ri est appelé normalisé...

Deux vecteurs ri, rj de l'espace vectoriel unitaire L sont orthogonaux entre eux si leur produit scalaire est égal à zéro, i.e. (ri, rj) = 0.

Pour s = 3 dans un espace vectoriel linéaire, il est commode de choisir trois vecteurs mutuellement perpendiculaires comme base. Ce choix simplifie considérablement un certain nombre de dépendances et de calculs. Le même principe d'orthogonalité est utilisé lors du choix d'une base en espaces et autres dimensions s> 3. L'utilisation de l'opération introduite du produit scalaire de vecteurs offre la possibilité d'un tel choix.

Des avantages encore plus grands sont obtenus lors du choix comme base de l'espace vectoriel des vecteurs normalisés orthogonaux - la base orthonormée... Sauf indication contraire, nous supposerons toujours que la base ei, i = 1 (1) s est choisie de cette manière, i.e.

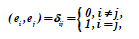
, où ij est le symbole de Kronecker (1823 - 1891).

Dans les espaces vectoriels unitaires, ce choix est toujours réalisable. Montrons la faisabilité d'un tel choix.

Définition. Soit S = {v1, v2,…, vn} un sous-ensemble fini d'un espace vectoriel V sur un corps F.Une

combinaison linéaire de vecteurs de S est une expression de la forme a1 ∙ v1 + a2 ∙ v2 +… + an ∙ vn, où chaque ai ∊ F.

L'enveloppe pour un ensemble S (notation {S}) est l'ensemble de toutes les combinaisons linéaires de vecteurs de S. L'enveloppe pour S est un sous-espace de V.

Si U est un espace dans V, alors U est couvert par S (S contracte U) si {S} = U.

L'ensemble des vecteurs S est linéairement dépendant de F s'il y a des scalaires a1, a2, ..., an dans F, pas tous les zéros pour lesquels a1 ∙ v1 + a2 ∙ v2 +… + an ∙ vn = 0. Si de tels scalaires n'existent pas, alors l'ensemble de vecteurs S linéairement indépendamment sur F.Si

un espace vectoriel V est couvert par un système linéairement indépendant de vecteurs S (ou si le système S contracte l'espace V), alors le système S est appelé une base de V.

Réduction d'une base arbitraire à une forme orthonormée

Soit l'espace V sur une base non orthonormée ē _i , i = 1 (1) s. Nous désignons la norme de chaque vecteur de base par le symbole

La déclaration suivante est connue [11]. Si ē _i , i = 1 (1) s est un système arbitraire fini ou dénombrable de vecteurs linéairement indépendants dans un espace vectoriel unitaire, alors il existe un système orthonormé ē _i , i = 1 (1) s, générant le même espace linéaire (variété).

La procédure de réduction de la base à une forme orthonormalisée est basée sur le processus d'orthogonalisation de Gram-Schmidt, qui à son tour est implémenté par des formules récurrentes.

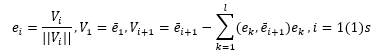
Sous forme développée, l'algorithme d'orthogonalisation et de normalisation de base contient les conditions suivantes:

diviser le vecteur ē ₁ par sa norme; on obtient le vecteur normalisé ē _i = ē ₁ / (|| ē ₁ ||);

On forme V2 = ē ₂ - (ē ₁ , ē ₂ ) e ₁ et on le normalise, on obtient e ₂ . Il est clair

qu'alors (e1, e2) ~ (e1, e2) - (e1, e ₂ ) (e1, e1) = 0;

En construisant V3 = ē ₃ - (e1, ē ₃ ) e1 - (e2, ē ₃ ) e2 et en la normalisant, on obtient e3.

Pour cela, on a immédiatement (e1, e3) = (e2, e3) = 0.

En poursuivant ce processus, on obtient un ensemble orthonormé ē _i , i = 1 (1) s. Cet ensemble contient des vecteurs linéairement indépendants, car ils sont tous orthogonaux entre eux.

Assurons-nous cela. Laissez la relation

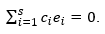
Si l'ensemble ē _i , i = 1 (1) s est dépendant, alors au moins un coefficient cj n'est pas égal à zéro cj ≠ 0. En

multipliant les deux côtés du rapport par ej, on obtient

(ej, c1 ∙ e1) + (ej, c2 ∙ e2) + ... + (ej, cj ∙ ej) +… + (ej, cs ∙ rs) = 0.

Chaque sommation de la somme est égale à zéro en tant que produit scalaire de vecteurs orthogonaux, sauf pour (ej, cj ∙ ej), qui est égal à zéro dans état. Mais dans ce terme

(ej, ej) = 1 ≠ 0, donc, seul cj peut être nul.

Ainsi, l'hypothèse que cj ≠ 0 n'est pas vraie et que la collection est linéairement indépendante.

Exemple 5 . Une base d'un espace vectoriel tridimensionnel est donnée:

{<-1, 2, 3, 0>, <0, 1, 2, 1>, <2, -1, -1,1>}.

Le produit scalaire est défini par la relation:

(<x1, x2, x3, x4>, <y1, y2, y3, y4>) = x1 ∙ y1 + x2 ∙ y2 + x3 ∙ y3 + x4 ∙ y4.

En utilisant la procédure d'orthogonalisation de Gram-Schmidt, nous obtenons un système de vecteurs:

1 = <-1, 2, 3, 0>; a2 = <0, 1, 2, 1> -4 <-1, 2, 3,0> / 7 = <4, -1, 2, 7> / 7;

a3 = <2, -1, -1, 1> + ½ <-1, 2, 3, 0> - <4, -1, 2, 7> / 5 = <7, 2, 1, -4> / Dix.

(a1, a2) = (1 + 4 + 9 + 0) = 14;

a1 ^E = a1 / √14;

a2- (a1 ^E , a2) ∙ a1 ^E = a2- (8 / √14) (a1 / √14) = a2 - 4 ∙ a1 / 7;

Le lecteur est invité à traiter le troisième vecteur de manière indépendante.

Les vecteurs normalisés prennent la forme:

a1 ^E = a1 / √14;

a2 ^E = <4, -1, 2, 7> / √70;

a3 ^E = <7, 2, 1, -4>/ √70;

Ci-dessous, dans l'exemple 6, un processus détaillé détaillé de calcul de la dérivation d'une base orthonormée à partir d'une base simple (prise au hasard) est donnée.

Exemple 6 . Réduisez la base donnée de l'espace vectoriel linéaire en forme orthonormée.

Étant donné: vecteurs de base

Sous-espaces d'espaces vectoriels

Structure de l'espace vectoriel La

représentation d'objets (corps) dans des espaces multidimensionnels est une tâche très difficile. Ainsi, un cube à quatre dimensions a des cubes tridimensionnels ordinaires comme faces, et un déploiement d'un cube à quatre dimensions peut être construit dans un espace tridimensionnel. Dans une certaine mesure, «l'imagerie» et la clarté d'un objet ou de ses parties contribuent à son étude plus réussie.

Ce qui précède nous permet de supposer que les espaces vectoriels peuvent être démembrés d'une certaine manière, pour y distinguer des parties, appelées sous-espaces. Evidemment, la prise en compte des espaces et des objets multidimensionnels et surtout infinis en eux nous prive de la clarté des représentations, ce qui rend très difficile l'étude des objets dans de tels

les espaces. Même des questions apparemment simples telles que les caractéristiques quantitatives des éléments des polyèdres (le nombre de sommets, d'arêtes, de faces, etc.) dans ces espaces sont loin d'être complètement résolues.

Une manière constructive d'étudier ces objets est de sélectionner leurs éléments (par exemple, des arêtes, des faces) et de les décrire dans des espaces de dimension inférieure. Ainsi, un cube à quatre dimensions a des cubes tridimensionnels ordinaires comme faces, et un dépliage d'un cube à quatre dimensions peut être construit dans un espace tridimensionnel. Dans une certaine mesure,

«l'imagerie» et la clarté de l'objet ou de ses parties contribuent à leur étude plus réussie.

Si L est une extension du champ K, alors L peut être considéré comme un espace vectoriel (ou linéaire) sur K. Les éléments du champ L (c'est-à-dire les vecteurs) forment un groupe abélien par addition. De plus, chaque «vecteur» a є L peut être multiplié par un «scalaire» r є K, et le produit ra appartient à nouveau à L (ici ra est simplement le produit au sens du champ L opération des éléments r et a de ce champ). Les lois sont également remplies

r ∙ (a + b) = r ∙ a + r ∙ b, (r + s) ∙ a = r ∙ a + r ∙ s, (r ∙ s) ∙ a = r ∙ (s ∙ a) et 1 ∙ a = a, où r, s є K, a, b є L.

Ce qui précède nous permet de supposer que les espaces vectoriels peuvent être démembrés d'une certaine manière, pour y distinguer des parties, appelées sous-espaces. Evidemment, le principal résultat de cette approche est de réduire la dimension des sous-espaces alloués. On distingue les sous-espaces L1 et L2 dans un espace vectoriel linéaire L. Comme base pour L1, on choisit un ensemble plus petit ei, i = 1 (1) s1, s1 <s, que dans le L. original.

Les vecteurs de base restants génèrent un autre sous-espace L2, appelé «complément orthogonal» du sous-espace L1. Nous utiliserons la notation L = L1 + L2. Cela ne signifie pas que tous les vecteurs de l'espace L appartiennent à L1 ou L2, mais que tout vecteur de L peut être représenté comme la somme d'un vecteur de L1 et d'un vecteur orthogonal de L2.

Ce n'est pas l'ensemble des vecteurs de l'espace vectoriel L qui est scindé, mais la dimension d (L) et l'ensemble des vecteurs de base. Ainsi, le sous-espace L1 d'un espace vectoriel L est l'ensemble L1 de ses éléments (de dimension inférieure), qui lui-même est un espace vectoriel par rapport aux opérations d'addition et de multiplication par un nombre introduit dans L.

Chaque sous-espace vectoriel linéaire Li - contient un vecteur nul et, avec l'un de ses vecteurs, contient toutes leurs combinaisons linéaires. La dimension de tout sous-espace linéaire ne dépasse pas la dimension de l'espace d'origine lui-même.

Exemple 7.Dans l'espace tridimensionnel ordinaire, les sous-espaces sont tous des lignes droites (dimension s = 1), des lignes, des plans (dimension s = 2) passant par l'origine. Dans l'espace n des polynômes de degré au plus n, les sous-espaces sont, par exemple, tous k pour k <n, puisque l'addition et la multiplication par des nombres de polynômes de degré au plus k, on obtiendra à nouveau les mêmes polynômes.

Cependant, chacun des espaces Pn est contenu sous forme de sous-espaces dans l'espace P de tous les polynômes à coefficients réels, et ce dernier est un sous-espace de l'espace C des fonctions continues.

Les matrices du même type sur le corps des nombres réels forment également un espace vectoriel linéaire, puisqu'elles satisfont tous les axiomes des espaces vectoriels. L'espace vectoriel L2 d'ensembles de longueur n, dont chacun est orthogonal au sous-espace L1 d'ensembles de longueur n, forme un sous-espace L2, appelé espace zéro pour L1. En d'autres termes, chaque vecteur de L2 est orthogonal à chaque vecteur de L1 et vice versa.

Les deux sous-espaces L1 et L2 sont des sous-espaces de l'espace vectoriel L d'ensembles de longueur n. Dans la théorie du codage [4], chacun des sous-espaces L1 et L2 génère un code linéaire duel au code généré par d'autres sous-espaces. Si L1 est un (n, k) -code, alors L2 est un (n, n - k) -code. Si un code est un espace vectoriel de lignes d'une matrice, alors son code dual est l'espace zéro de cette matrice et vice versa.

Un problème important dans l'étude des espaces vectoriels Vn est l'établissement de leur structure (structure). En d'autres termes, sont intéressants les éléments, leurs collections (sous-espaces de dimension 1 <k <n), ainsi que leurs relations (ordre, emboîtement, etc.). On suppose qu'un espace vectoriel Vn donné sur un corps fini GF (q) formé de q = p r éléments, où p est un nombre premier et r est un entier.

Les résultats suivants sont connus.

Le nombre de sous-espaces d'un espace vectoriel

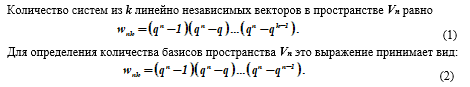
Donnons la justification suivante. Chaque vecteur v1 ≠ 0 d'un système de k vecteurs linéairement indépendants (v1, v2,…, vk) peut être choisi de q ⁿ - 1 manières. Le vecteur suivant v2 ≠ 0 ne peut pas être exprimé linéairement en termes de v1, i.e. peut être choisi de q ⁿ - q façons, etc.

Le dernier vecteur vk ≠ 0 n'est pas non plus exprimé linéairement en termes des vecteurs v1, v2,…, vk précédemment sélectionnés et, par conséquent, peut être choisi de q ⁿ - q ^k - 1 manières. Le nombre total de façons de sélectionner un ensemble de vecteurs v1, v2, ..., vk est donc défini comme le produit du nombre de sélections de vecteurs individuels, ce qui donne la formule (1). Pour le cas où k = n, on a w = wn, n et à partir de la formule (I) on obtient la formule (2).

Résultats de généralisation importants sur les dimensions des sous-espaces.

La collection de tous les tuples de longueur n orthogonaux au sous-espace V1 des tuples de longueur n forme le sous-espace V2 des tuples de longueur n. Ce sous-espace V2 est appelé l'espace nul pour V1.

Si un vecteur est orthogonal à chacun des vecteurs générant le sous-espace V1, alors ce vecteur appartient à l'espace nul pour V1.

Un exemple de (V1) est l'ensemble des vecteurs à 7 bits de la matrice génératrice du code de Hamming (7,4), avec un sous-espace nul (V2) de vecteurs à 7 bits qui forment la matrice de contrôle de parité de ce code.

Si la dimension du sous-espace (V1) des ensembles de longueur n est égale à k, alors la dimension du sous-espace nul (V2) est égale à n - k.

Si V2 est un sous-espace de tuples de longueur n et V1 est un espace nul pour V2, alors (V2) est un espace nul pour V1.

Soit U∩V la collection de vecteurs appartenant à la fois à U et à V, alors U∩V est un sous-espace.

Soit U⊕V le sous-espace constitué par la collection de toutes les combinaisons linéaires de la forme a u + b v , où u є U, v є V, ab sont des nombres.

La somme des dimensions des sous-espaces U∩V et U⊕V est égale à la somme des dimensions des sous-espaces U et V.

Soit U2 le sous-espace zéro pour U1 et V2 l'espace zéro pour V1. Alors U2∩V2 est l'espace zéro pour U1⊕V1.

Conclusion

L'article examine les concepts de base des espaces vectoriels, qui sont souvent utilisés dans la construction de modèles pour l'analyse des systèmes de cryptage, de codage et de stéganographie, processus qui s'y déroulent. Ainsi, dans le nouveau standard de cryptage américain, des espaces affines sont utilisés, et dans les signatures numériques sur des courbes elliptiques, à la fois des espaces affines et

projectifs (pour accélérer le traitement des points de courbe).

On ne parle pas de ces espaces dans l'oeuvre (on ne peut pas tout mettre en un seul tas, et je limite aussi le volume de publication), mais la mention de cela n'est pas faite en vain. Les auteurs qui écrivent sur les moyens de protection, sur les algorithmes de chiffrement, croient naïvement comprendre les détails des phénomènes décrits, mais la compréhension des espaces euclidiens et de leurs propriétés est transférée sans aucune réserve à d'autres espaces, avec des propriétés et des lois différentes. Le public de lecture est induit en erreur sur la simplicité et l'accessibilité du matériel.

Une fausse image de la réalité est créée dans le domaine de la sécurité de l'information et des équipements spéciaux (technologie et mathématiques).

En général, j'ai pris l'initiative, à quel point les lecteurs ont la chance de juger.

Littérature

1. Avdoshin S.M., Nabebin A.A. Mathématiques discrètes. Algèbre modulaire, cryptographie, codage. - M.: DMK Press, 2017.-352 p.

2. Akimov O.E. Mathématiques discrètes Logique, groupes, graphes - M.: Lab. Base. Zn., 2001.-352 p.

3. Anderson D.A. Mathématiques discrètes et combinatoire), Moscou: Williams, 2003, 960 p.

4. Berlekamp E. Théorie du codage algébrique. -M.: Mir, 1971.- 478 p.

5. Vaulin A.E. Mathématiques discrètes dans les problèmes de sécurité informatique. H 1- SPb.: VKA im. UN F. Mozhaisky, 2015, 219 p.

6. Vaulin A.E. Mathématiques discrètes dans les problèmes de sécurité informatique. H 2- SPb.: VKA im. UN F. Mozhaisky, 2017.-151 p.

7. Gorenstein D. Groupes simples finis. Introduction à leur classification.-M.: Mir, 1985.- 352 p.

7. Graham R., Knut D., Ptashnik O. Mathématiques concrètes. Fondations de l'informatique.-M.: Mir, 1998.-703 p.

9. Elizarov V.P. Anneaux d'extrémité. - M.: Helios ARV, 2006. - 304 p.

Ivanov B.N. Mathématiques discrètes: algorithmes et programmes-M.: Lab.Baz. Connaissance., 2001.280 p.

10. Yerusalimsky Ya.M. Mathématiques discrètes: théorie, problèmes, applications-M.: Vuzovskaya kniga, 2000.-280 p.

11. Korn G., Korn T. Manuel de mathématiques pour les scientifiques et les ingénieurs.-M.: Nauka, 1973.-832 p.

12. Lidl R., Niederreiter G. Champs finis: en 2 volumes.Vol.1 -M.: Mir, 1988. - 430 p.

13. Lidl R., Niederreiter G. Champs finis: en 2 volumes.Vol.2 -M.: Mir, 1988. - 392 p.

14. Lyapin E.S., Aizenshtat A.Ya., Lesokhin M.M., Exercices sur la théorie des groupes - Moscou: Nauka, 1967.-264 p.

15. Mutter V.M. Fondamentaux de la transmission d'informations anti-brouillage. -L. Energoatomizdat, 1990, 288 p.

16. Nabebin A.A. Mathématiques discrètes .- M.: Base de laboratoire. Connaissance., 2001.280 p.

17. Novikov F.A. Mathématiques discrètes pour les programmeurs - SPb.: Peter, 2000.-304 p.

18. Rosenfeld B.A. Espaces multidimensionnels.-M.: Nauka, 1966.-648 p.

18. Hall M. La théorie des groupes.-M.: Izd. IL, 1962. - 468 p.

19. Shikhanovich Yu.A. Groupes, anneaux, treillis. - SPb.: Kirtsideli, 2006. - 368 p.

20. Shneperman LB Un cours d'algèbre et de théorie des nombres en problèmes et exercices: En 2 heures Partie 2.-Mn.: Vysh. shk., 1987.-256 p.

21. Shneperman LB Collection de problèmes d'algèbre et de théorie des nombres - Minsk: Design PRO, 2000. -240 p.

Espaces vectoriels