
Autres articles du cycle
. I
. II
. II
La théorie formelle de la modélisation utilise des relations algébriques, les intégrant dans les signatures de modèles de structures algébriques, qui décrivent des objets physiques et techniques réels et les processus de leur fonctionnement. Cette publication s'inscrit dans la continuité de la précédente , dont la lecture est souhaitable, car de nombreux concepts et termes utilisés ici y sont décrits.
La présentation n'est pas proposée dans le style traditionnel (flèche), mais de la manière dont j'ai moi-même dû imaginer et maîtriser toute cette cuisine à la fois à partir de manuels / manuels et d'articles de magazines. Je considère que le catalogue que j'ai créé est particulièrement utile, il vous permet de sélectionner presque n'importe quel espace et de présenter ses éléments sous une forme pratique: une matrice, un graphique, etc.
Concept de relation
Je pense que le terme attitude est familier à tous les lecteurs, mais demander une définition sera plus déroutant. Il y a plusieurs raisons à cela. Il s'agit le plus souvent d'enseignants qui, s'ils ont utilisé des relations dans le processus d'enseignement, ne se sont pas concentrés sur ce terme, n'ont pas donné d'exemples mémorables. Certains commentateurs de l'article ont attribué les commentaires à leur propre compte et ont ajouté des inconvénients. Mais vous ne pouvez pas cacher une couture dans un sac. Il n'y a pas eu de publications sérieuses, et non. Demandez-vous, avez-vous travaillé avec un espace relationnel? Et répondez-vous honnêtement. Que pouvez-vous dire au monde sur cet espace? Pour commencer, listez au moins ses éléments et spécifiez ses propriétés. Vous regardez même le SGBD à travers les yeux de leurs créateurs, mais ils ne voient pas tout non plus, ou ils ne montrent pas tout, comme par exemple dans les microcircuits.
Ici, je vais faire une petite répétition. Il faut commencer par l'ensemble abstrait A = {a1, a2, a3, ..., an}. Vous pouvez en savoir plus ici . Pour une meilleure compréhension, nous réduirons l'ensemble à 3 éléments, soit = {a1, a2, a3}. Nous effectuons maintenant la multiplication cartésienne × = 2 et énumérons explicitement tous les éléments du carré cartésien
× = {(a1, a1), (a1, a2), (a1, a3), (a2, a1), (a2, a2 ), (a2, a3), (a3, a1), (a3, a2), (a3, a3)}.
Nous avons obtenu 9 paires ordonnées d'éléments de A × A, dans une paire le premier élément du premier facteur, le second du second. Essayons maintenant d'obtenir tous les sous-ensembles du carré cartésien A × A. Les sous-ensembles contiendront un nombre différent de paires: une, deux, trois, et ainsi de suite jusqu'aux 9 paires, nous incluons également l'ensemble vide ∅ dans cette liste. Combien de sous-ensembles y a-t-il? Beaucoup, à savoir 2 9= 512 éléments.
Définition . Un sous-ensemble d'un ensemble de carrés cartésiens est appelé une relation binaire. Si le carré cartésien de deux facteurs, le rapport est binaire, si de 3 il est interne, de 4 il est tétrar, et de n il est n-aire. Arity est le nombre de places dans un élément de relation.
Définition . L'ensemble de tous les sous-ensembles de l'ensemble A est appelé un booléen. Le booléen se compose de 2 | A | éléments, ici | A | Est la cardinalité de l'ensemble.
Les relations peuvent être définies de différentes manières:
- énumération des éléments; R1 = {(a2, a2), (a2, a3), (a3, a1)}; R2 = {(a3, a3)}
- vecteur binaire; <000011100>; <000000001>
- matrice;
- graphique et d'autres moyens.
Ensuite, nous passons à la considération des espaces de relations, en supposant que le concept, les propriétés des relations et les opérations avec eux sont familiers au lecteur au moins dans la mesure de notre publication dans le lien.
Espaces de relations binaires
Clarifions au préalable que les relations peuvent être strictes (ce sont toutes des relations antireflet) ou non strictes (toutes les autres). Nous nous concentrerons sur la relation d'indifférence et de préférence, ces dernières étant subdivisées en préférences faibles et préférences strictes (pour une raison quelconque, pas fortes). En général, il n'y a pas d'ordre scientifique avec la terminologie et il n'y en aura probablement pas. En cryptographie, par exemple, supprimer un chiffrement d'un cryptogramme en présence d'une clé est un déchiffrement et sans clé, un déchiffrement. Il semblerait qu'un décodeur décode, mais non.
L'espace des relations binaires avec un ensemble de porteurs est un sous-ensemble arbitraire de l'ensemble des relations binaires donné sur. Considérez les principaux espaces pour les relations de préférence (Figure 2.15).
R- l'espace de toutes les relations de faible préférence, satisfait à la condition de réflexivité et d'exhaustivité.
QT - préférences faibles satisfaisant la condition de quasi-transitivité.
QO est l'espace des quasi- ordres linéaires, c'est-à-dire des relations de QT qui sont transitives.
TO est l'espace de tous les ordres parfaits, c'est-à-dire des relations de QO qui sont antisymétriques.
SP est l'espace de toutes les relations de préférence stricte; elles satisfont aux propriétés d'antiréfléchissement et d'antisymétrie.
RO- relations d'ordre partiel strict, ou préférences strictes transitives. Les relations d'ordre partiel strict étant transitives, il est naturel de les utiliser pour les représenter par des graphes réduits, c'est-à-dire ceux dans lesquels les arcs de transitivité sont omis. De tels graphiques abrégés sont appelés diagrammes de Hasse.
QS est l'espace des quasi-séries, c'est-à-dire des ordres partiels stricts pour lesquels la relation I = ¬ (PUP -1 ) est une équivalence.
TSO est l'espace des ordres linéaires stricts, c'est-à-dire des ordres partiels pour lesquels la propriété d'exhaustivité est satisfaite.
Il faut noter qu'il y a n de telles relations au total! .. Par exemple, pour n = 3, le nombre de relations parfaites est de 6, et elles sont toutes représentées sur la Fig. 2.13.
T- l'espace de toutes les relations de tolérance (indifférence), elles ont les propriétés de symétrie et de réflexivité.
TOT est l'espace des relations de tolérance orientées transitivement, c'est-à-dire des relations telles que le complément de I est représenté comme une union de relations transitives mutuellement inverses, c'est-à-dire
¬I = R∩R -1 .
I est l'espace de toutes les relations d'équivalence, c'est-à-dire des relations symétriques, réflexives et transitives.
E - espace de relations d'égalité, consiste en une relation représentée par une matrice diagonale. Il existe une relation biunivoque entre les espaces R, P et I, déterminée par la mise en correspondance des relations de préférence.


Figure 2.15 Schéma des espaces de relations binaires
Les connexions révélées entre les espaces sont utilisées pour transférer des problèmes de prise de décision (DM) d'un espace à un autre, où ils peuvent être résolus de manière plus simple, puis la solution résultante est renvoyée dans l'espace d'origine, où le DP a été formulé.
Ces relations sont illustrées schématiquement sur la Fig. 2.14. Les espaces de relations binaires (types de relations) sont représentés sur la Fig. 2.15.
Relations d'équivalence
Définition . Une relation binaire σ ⊆ A × A, qui a trois propriétés de réflexivité, symétrie, transitivité, est appelée une relation d'équivalence binaire (BOE). La relation d'équivalence σ (x, y), (x, y) ∊σ, xσy, x≈y est notée. Il est pratique d'utiliser une représentation matricielle (tabulaire) de la relation. Ci-dessous dans la figure 2.24 est juste une représentation matricielle. Au-dessus de l'ensemble de 4 éléments, il y a 15 BOE, qui sont tous représentés.
Représentation et analyse de la structure des relations d'équivalence (n = 4)
L'équivalence des relations binaires est peut-être le BO le plus courant. La science se débrouille rarement sans ce concept, mais même lorsque des équivalences sont utilisées pour poser des questions, il peut être difficile de comprendre ce que l'auteur voulait dire. Même avec la définition et l'énumération correctes des propriétés inhérentes à cette relation binaire, les difficultés de perception demeurent.
Commençons par un exemple sur les équivalences, qui illustre les limites de leur nombre.
Exemple 1 . Soit trois cubes. Faisons une liste des propriétés dont les cubes sont dotés et dont l'utilisation pratique (les propriétés des cubes) les rend, pour ainsi dire, interchangeables. Attribuons des nombres aux cubes et représentons leurs propriétés dans le tableau 1.
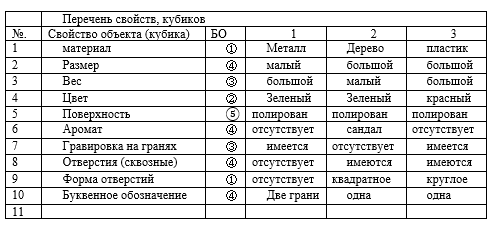
Pour chacune des propriétés, des BOE et des classes d'équivalence apparaissent. En continuant la liste des propriétés, nous n'obtiendrons pas de nouvelles relations d'équivalence. Il n'y aura que des répétitions de ceux déjà construits, mais pour d'autres signes. Montrons le lien entre BOE et décors.
Considérons un ensemble de trois éléments A = {1,2,3} et obtenez pour cela toutes les partitions possibles en toutes les parties. ①1 | 2 | 3; ②12 | 3; ③13 | 2; ④ 1 | 23; ⑤123. La dernière scission en une seule partie. Numéros de partition et BO en cercles.
Définition . Une partition d'un ensemble A est une famille i, i = 1 (1) I, de sous-ensembles disjoints par paires non vides de , dont l'union forme l'ensemble d'origine = Ui, i∩j = ∅, ∀ i ≠ j. Les sous-ensembles i sont appelés classes d'équivalence de la partition de l'ensemble d'origine.
Ce sont toutes les partitions de l'ensemble (5 pièces). L'analyse BO montre qu'il n'y a également que 5 relations d'équivalence différentes. Cette coïncidence est-elle une coïncidence? On peut associer chaque partition à une matrice de neuf cellules (3 × 3 = 9), chacune contenant soit une paire ordonnée d'éléments de l'ensemble A, soit la cellule reste vide s'il n'y a pas d'objet pour la paire correspondante. Les lignes et colonnes de la matrice sont marquées avec des éléments de l'ensemble A, et l'intersection ligne-colonne correspond à une paire ordonnée (i, j). Ce n'est pas une paire qui s'insère dans une cellule matricielle, mais juste un ou zéro, cependant, zéro n'est souvent pas écrit du tout.
Non, la coïncidence n'est pas accidentelle. Il s'avère que chaque partition de l'ensemble est en correspondance biunivoque avec le BOE, et la cardinalité de l'ensemble peut être quelconque | A | = n.
Cette relation est peut-être la plus fréquente en termes d'utilisation dans la circulation scientifique, mais la combinaison des propriétés réalisées à cet égard limite grandement sa prévalence.
Ainsi, parmi toutes les relations binaires abstraites sur un ensemble de trois éléments (il y a 2 9 = 512 relations au total ), seulement cinq sont des équivalences - porteurs des propriétés requises, moins d'un pour cent.
Pour | A | = 4 relations existent 2 16= 65536, mais il n'y a que 15 équivalences. C'est un type de relation très rare. D'autre part, les relations d'équivalence sont répandues dans les problèmes appliqués. Partout où il y a et sont considérés comme des ensembles d'objets très différents et des partitions différentes de ces ensembles (et non des nombres) en parties, des relations d'équivalence apparaissent. On peut les appeler des modèles mathématiques (algébriques) de telles partitions, qui classent des ensembles d'objets selon divers critères.
La partition minimale de l'ensemble A formée à partir de sous-ensembles à un élément A = U {a} et la partition A constituée de l'ensemble {A} lui-même sont appelées partitions triviales (impropres).
Lattice P (4): toutes les partitions de l'ensemble A = {a1, a2, a3, a4} = {1,2,3,4}

Le partitionnement minimum correspond à la relation d'équivalence P15, appelée égalité ou relation unitaire. Chaque classe d'équivalence contient un seul élément. A une partition de l'ensemble A, qui ne comprend que l'ensemble A lui-même, correspond une relation d'équivalence contenant tous les éléments du carré cartésien A × A.

Le type le plus proche des relations d'équivalence est celui des relations de tolérance . L'ensemble des relations de tolérance contient toutes les relations d'équivalence. Pour le porteur A, il y a trois éléments de tolérance 8. Tous ont les propriétés de réflexivité et de symétrie.
Lorsque la propriété de transitivité est remplie, cinq des huit tolérances se transforment en équivalences (figures 2.24 et 2.25).
Définition . L'ensemble des classes d'équivalence [a] σ des éléments de l'ensemble A est appelé l'ensemble quotient (noté A / σ) de l'ensemble A par l'équivalence σ.
Définition . Une application naturelle (canonique) f: A → A / σ est une application f telle que f (a) = [a] σ.
Relations de tolérance et leur analyse
Ces BO ont déjà été mentionnés précédemment, mais nous les examinerons ici plus en détail. Tout le monde connaît les concepts de similitude, de similitude, de similitude, d'indiscernabilité, d'interchangeabilité des objets. Ils semblent avoir un contenu similaire, mais pas la même chose. Lorsque seule la similitude est indiquée pour les objets, il est impossible de les décomposer en classes claires de sorte qu'au sein d'une classe les objets soient similaires, et il n'y a pas de similitude entre les objets de classes différentes. En cas de similitude, une situation vague survient sans limites claires. D'un autre côté, l'accumulation de différences insignifiantes dans des objets similaires peut conduire à des objets complètement différents.
Dans la partie précédente, nous avons discuté de la signification significative de la relation de similitude (équivalence) des objets. Tout aussi importante est la situation où il est nécessaire d'établir la similitude des objets.
Étudions la forme des corps géométriques. Si la similitude de la forme des objets, par exemple des cubes, signifie leur interchangeabilité complète dans une certaine situation d'apprentissage, alors la similitude est une interchangeabilité partielle (quand parmi les cubes il y a des parallélépipèdes qui leur sont très similaires), c'est-à-dire la possibilité d'interchangeabilité avec certains (admissible dans cette situation ) pertes.
La plus grande mesure de similitude est l'indiscernabilité, pas du tout la similitude, comme cela peut paraître à première vue. L'identité est une propriété qualitativement différente. L'identité ne peut être considérée que comme un cas particulier d'indiscernabilité et de similitude.
Le fait est que les objets indiscernables (ainsi que les objets similaires et similaires) ne peuvent pas être divisés en classes afin que les éléments de chaque classe ne soient pas différents et que les éléments des différentes classes soient évidemment différents.
En effet, nous considérerons l'ensemble des points (x, y) sur le plan. Soit la valeur d une valeur inférieure au seuil de résolvabilité de l'œil, c'est-à-dire que d est une distance à laquelle deux points situés à cette distance se confondent en un, c'est-à-dire visuellement indiscernable (à la distance choisie de l'avion de l'observateur). Considérons maintenant n points situés sur une ligne droite et espacés (chacun des voisins) d'une distance d. Chaque paire de
points adjacents est indiscernable, mais si n est suffisamment grand, le premier et le dernier points seront éloignés l'un de l'autre et seront certainement distinguables.
L'approche traditionnelle pour étudier la similitude ou l'indiscernabilité consiste d'abord à déterminer la mesure de la similitude, puis à examiner la position relative d'objets similaires. Le mathématicien anglais Zieman, étudiant les modèles de l'appareil visuel, a proposé une définition axiomatique de la similitude. Ainsi, il est devenu possible d'étudier les propriétés de la similitude indépendamment de la précision avec laquelle elle est spécifiée dans une situation donnée: la distance entre les objets, la coïncidence de certaines caractéristiques ou l'opinion subjective de l'observateur.
Introduisons une explication du concept de similitude ou d'indiscernabilité.
Définition . La relation T sur l'ensemble M est appelée relation de tolérance ou de tolérance si elle est réflexive et symétrique.
La justesse de cette définition est évidente du fait que l'objet est évidemment indiscernable de lui-même et, bien sûr, ressemble à lui-même (cela donne la réflexivité de la relation). L'ordre de considération de deux objets n'affecte pas la conclusion finale sur leur similitude ou leur dissemblance (symétrie).
A partir de l'exemple avec indiscernabilité visuelle des points sur le plan, nous voyons que la transitivité de la tolérance n'est pas remplie pour toutes les paires d'objets.
Il est également clair que la similitude étant un cas particulier de similitude, l'équivalence doit être un cas particulier de tolérance. En comparant les définitions de l'équivalence et de la tolérance, nous sommes convaincus que tel est le cas. Le principe philosophique: «le particulier est plus riche que le général» est clairement confirmé. Une propriété supplémentaire - la transitivité rend certaines des relations de tolérance équivalentes. Deux jumeaux se ressemblent tellement qu'ils peuvent se passer des examens sans risque. Cependant, si deux étudiants se ressemblent seulement, une telle astuce, bien que réalisable, est risquée.
Chaque élément de l'ensemble contient certaines informations sur des éléments similaires. Mais pas toutes les informations, comme dans le cas d'éléments identiques. Ici, différents degrés d'informations sont possibles qu'un élément contient par rapport à un autre.
Prenons des exemples où la tolérance est définie de différentes manières.
Exemple 2 . L'ensemble M se compose de mots russes de quatre lettres - noms communs dans le cas nominatif. Nous appellerons ces mots similaires s'ils ne diffèrent pas de plus d'une lettre. Le problème bien connu "Transformer une mouche en éléphant" en termes précis est formulé comme suit. Trouvez une séquence de mots commençant par le mot «voler» et se terminant par le mot «éléphant», deux mots adjacents quelconques dans le sens de la définition qui vient d'être donnée. La solution à ce problème:
mouche - mura - tura - tara - kara - kare - café - kaffr - musher - esquif - crochet - croc - temps - stock - gémissement - éléphant.
Exemple 3... Soit p un nombre naturel. On note Sp la collection de tous les sous-ensembles non vides de l'ensemble M = {1, 2, ..., p}. La relation «avoir au moins un élément commun» sur l'ensemble Sp est une relation de tolérance. Ensuite, deux de ces sous-ensembles sont appelés tolérants s'ils ont au moins un élément commun. Il est facile de voir que la réflexivité et la symétrie de la relation sont remplies.
L'ensemble Sp est appelé un simplexe (p –1) dimensionnel. Ce concept généralise le concept de segment, de triangle et de tétraèdre au cas multidimensionnel. Les nombres 1, 2, 3, ..., p sont interprétés comme des sommets d'un simplexe. Sous-ensembles à deux éléments - en tant qu'arêtes, trois éléments - en tant que faces planes (bidimensionnelles), autres sous-ensembles à k éléments - en tant que faces (k –1) dimensionnelles. Le nombre de tous les éléments (sous-ensembles) de Sp est égal à 2 p - 1.
La tolérance des sous-ensembles (faces) signifie qu'ils ont des sommets communs.
Définition . L'ensemble M avec la relation de tolérance τ donnée dessus s'appelle l'espace de tolérance. Ainsi, l'espace de tolérance est une paire (M, τ).
Exemple 4 . L'espace de tolérance Sp peut être généralisé au cas infini. Soit H un ensemble arbitraire. Si SH est la collection de tous les sous-ensembles non vides de l'ensemble H, alors la relation de tolérance T sur SH est donnée par la condition: X T Y si X∩Y ≠ ∅. La symétrie et la réflexivité de cette relation sont évidentes. L'espace SH est désigné <H, T> et est appelé espace "universel" de tolérance.
Exemple 5... Soit p un nombre naturel. Notons Bp l'ensemble de tous les points de l'espace p-dimensionnel dont les coordonnées sont 0 ou 1. La tolérance dans Bp est donnée par la règle: xτy si x et y contiennent au moins une composante coïncidente (coordonnée). Le nombre total d'éléments dans Bp est de 2 r . Pour chaque élément x = (a1, a2, ..., ap) de l'ensemble Bp, il n'y a qu'un seul élément y = (1 - a1, 1 - a2, ..., 1 - ap) qui ne lui est pas tolérant.
De toute évidence, Bp est constitué de tous les sommets du cube p-dimensionnel.
Exemple 6 . Considérez l'espace de tolérance, dont les composants prennent des valeurs réelles.
En particulier, c'est l'ensemble de tous les points x = (a1, a2) dans le plan cartésien. La tolérance de deux points signifie qu'ils ont au moins une coordonnée. Cela signifie que deux points tolérants sont soit sur une verticale commune, soit sur une horizontale commune.
Pour les autres valeurs de p, l'espace peut être interprété comme un ensemble de points dans l'espace p-dimensionnel. En particulier, chaque élément x peut être considéré comme une fonction numérique définie sur l'ensemble des nombres naturels {1, 2, 3, ...}, qui attribue à chaque entier i: 1 ≤ i ≤ p un nombre réel ai (une suite de nombres finie). Alors la tolérance de deux fonctions x et y signifie qu'elles sont égales au moins en un point.
Relations d'ordre partiel et leur analyse
Les ensembles ordonnés sont des ensembles avec une relation d'ordre introduite dessus. Définition . Un ensemble A et une relation d'ordre binaire R sur lui (≤) est appelé partiellement ordonné si la relation contient (comme dans BOE) trois conditions (une condition est différente):
- réflexivité ∀ x ∊ A (xRx); (antireflet ∀ x ∊ A ¬ (xRx));
- antisymétrie ∀ , y ∊ (Ry yRx → x = y);
- transitivité ∀ x, y, z ∊ A (xRy & yRz → xRz).
Avec une attitude antireflet, un ordre partiel strict apparaît . L'ensemble B (A) de tous les sous-ensembles de l'ensemble A, ordonné par l'inclusion d'éléments, est un ensemble partiellement ordonné (PA). L'ensemble partiellement ordonné (B (A), ⊆) est souvent appelé un booléen.
Un élément x∊A POZA A recouvre un élément y∊A si x> y et il n'y a pas de z∊A tel que x> z> y. Une paire d'éléments x, y∊A est dite comparable si x ≥ y ou x ≤ y.
Si dans PLA A, chaque paire de ses éléments est comparable, alors A est appelé un ensemble ou une chaîne ordonnée linéairement . Si un fléau B n'est constitué que d'éléments incomparables les uns avec les autres, alors l'ensemble B est appelé une antichaïne
... Une chaîne dans PLAG A est dite saturée si elle ne peut être imbriquée dans aucune autre chaîne que la sienne.
L'antichaine saturée est définie de manière similaire. Une chaîne maximale (antichain) est une chaîne (antichain) contenant le nombre maximal d'éléments.
Un élément m d'un PLM A est dit minimal s'il n'y a pas d'élément ∊ dans autre que m et tel que ≤m. Un élément M d'un fléau A est dit maximal s'il n'y a pas d'élément x «supérieur» à M, autre que M et tel que x ≥ M.
Un élément y∊A d'un fléau A est dit maximal si ∀ x∊ A x ≤ y. L'élément y∊ A PLAG A est appelé le plus petitsi ∀ x∊A x ≥ y. Pour les éléments les plus grands et les plus petits, il est d'usage d'utiliser respectivement les désignations 1 et 0. On les appelle des frontières universelles. Toute peste A a au plus un élément le plus petit et au plus un élément le plus grand. Plusieurs éléments minimum et plusieurs éléments maximum sont autorisés dans
PLA A. Il est pratique de représenter le PLA A final avec un diagramme de Hasse , qui est un graphe orienté, ses sommets sont répartis sur les niveaux du diagramme et correspondent aux éléments de A, et chaque arc est dirigé vers le bas et est dessiné si et seulement si l'élément x∊A couvre l'élément y∊A.
Les arcs transitifs ne sont pas dessinés. Les niveaux des graphiques Hasse contiennent des éléments du même rang, c'est-à-dire relié aux éléments minimaux du PCM par des chemins de longueur égale (en fonction du nombre d'arcs).
Soit B un sous-ensemble non vide de PLA A, alors un élément x∊A est appelé la borne supérieure exacte (notée sup A B) de l'ensemble B si x ≥ y pour tout y∊B et s'il découle de la vérité de la relation z ≥ y pour tout y∊B, que z ≥ x.
Un élément x A est appelé une borne inférieure exacte (notée inf A B) d'un ensemble B si x ≤ y pour tout y∊B et si la condition z ≤ y pour tout y∊ B implique que z ≤ x.
Exemple 7 . Deux ensembles numériques finis
A = {0,1,2, ..., 21} et B = {6,7,10,11} sont donnés.
CHUM (A, ≤) est illustré à la Fig. 2.26.
La collection B Δ de toutes les bornes supérieures de est appelée le cône supérieur de l'ensemble B. La collection ∇de toutes les faces inférieures pour B est appelé le cône inférieur pour B.

Tout sous-ensemble de PLA est également PLP par rapport à l'ordre hérité. Si l'ensemble contient les éléments les plus grands et / ou les plus petits, alors ils sont maximum (minimum, respectivement). L'inverse est pas vrai. Boolean a un seul plus petit (Ø) et un seul plus grand élément.
Dans l'ensemble donné, le plus petit élément est zéro (0) et il coïncide avec le seul élément minimal, et le plus grand élément n'existe pas. Les éléments maximum sont {19, 20, 21}. La limite supérieure exacte de B = {6,7,10,11} est l'élément 21 (c'est le plus petit élément du cône supérieur).
Situation générale. Soit un ensemble dont la cardinalité est *******. Parmi toutes les relations binaires possibles sur cet ensemble, distinguons les relations de préférence binaire et les relations d'ordre partiel strict associées.
Les ordres partiels diffèrent des ordres partiels stricts uniquement en ce qu'ils contiennent des éléments supplémentaires (dans la représentation matricielle - diagonale) (i, ai) = 1, i = 1 (1) n, et le nombre de ces ordres et d'autres dans l'ensemble complet des relations le même. Jusqu'à présent, aucune dépendance (formule, algorithme) n'a été trouvée permettant de calculer et d'énumérer le nombre d'ordres partiels pour tout n.
Différents auteurs ont déterminé et publié les résultats suivants par calcul direct (tableau 2.12).
Les expériences de calcul de l'auteur ont permis d'obtenir non seulement le nombre, mais aussi la forme (représentation) d'ordres partiels à différentes puissances du multiplicateur-porteur de relations. L'imprimeur s'est étouffé en imprimant des listes aussi énormes, mais non seulement la beauté nécessite des sacrifices, la science ne les refuse pas non plus.

Le tableau 2.12 montre: n = | A | - la cardinalité de l'ensemble-porteur; la deuxième ligne est le nombre de toutes les relations binaires sur l'ensemble A; et plus
| Dans (n) | - le nombre de classes de relations non isomorphes;
| (n) | - le nombre de relations d'ordre partiel;
| Gn (n) | - le nombre de classes de relations d'ordre partiel non isomorphes;
| Gl (n) | = n! - le nombre de relations d'ordre linéaire.
Comme vous pouvez le voir, dans le tableau pour petit n, par exemple, G (n = 4), il n'y a que 219, des données sont données, dont les valeurs croissent très rapidement avec l'augmentation de n, ce qui complique considérablement leur analyse directe quantitative (et qualitative), même avec un ordinateur.
Le tableau ci-dessous illustre la possibilité de générer Γ (n = 4) de tous les ordres partiels à partir de l'intersection de chacun avec chaque ordre partiel linéaire. Mais dans cette situation, des redondants (répétitifs) apparaissent, qui pour un petit n peuvent être coupés manuellement (recalculés). Il s'avère que 300 matrices, mais il n'y en a que 219. Les formules générales n'ont pas été obtenues. Au niveau mondial, la situation est similaire, même si je n'ai vu aucune publication sur les transferts PLM par des auteurs occidentaux. Nos algorithmes sont totalement originaux et pionniers.
Je donnerai un schéma possible pour résoudre le problème de l'énumération des éléments de l'espace des ordres partiels (n = 4).

L'ensemble des ordres partiels stricts dans l'ordre lexicographique des ordres linéaires (n = 4) est généré par leur intersection mutuelle.


Plusieurs définitions importantes des mathématiques, pour des concepts que l'on retrouve souvent dans les textes.
Définition . Un intervalle fermé est un ensemble de la forme {x: a ≤ x ≤ b}; un intervalle ouvert n'est pas fermé, et un intervalle semi-ouvert, c'est-à-dire un ensemble de la forme {x: a <x ≤ b}, où a <b, ou de la forme {x: a ≤ x <b} n'est ni ouvert ni fermé.
Définition . La limite d'un intervalle arbitraire d'une ligne réelle dans la topologie habituelle des nombres réels se compose uniquement des extrémités de cet intervalle, que cet intervalle soit ouvert, fermé ou semi-ouvert. La limite de l'ensemble des nombres rationnels, ainsi que la limite de l'ensemble de tous les nombres irrationnels, est l'ensemble complet des nombres réels.
Définition... Chaque ensemble ordonné linéairement, dans tout sous-ensemble non vide dont il y a le plus petit élément, est appelé bien ordonné.
Définition . Une famille R est appelée chaîne (parfois une tour, un nid) si et seulement si, pour l'un de ses éléments A et B, soit A ⊂ B ou B ⊂ A. Cette condition équivaut à l'affirmation que la famille R est ordonnée linéairement par inclusion ou, dans la terminologie acceptée - que la famille R avec la relation d'inclusion est une chaîne.
P r et n c et p m a à s et m al n à propos de s t et H a u s d o r f a. Pour toute famille d'ensembles A et tout nid R formé par des éléments de la famille A, il existe un nid maximal M dans A contenant R.
Un théorème important sur les ensembles et leurs familles (J.L. Kelly "General topology" p. 55).
Théorème. (a) PRINTSIpMACKSIMALN sur ELEMENT. Un élément maximal dans la famille A d'un ensemble existe si, pour chaque imbrication dans A, il y a un élément dans A qui contient un élément arbitraire de cette imbrication.
(b) PRINTSIpMINIMALNO ELEMENT. Le plus petit élément d'une famille A existe si, pour chaque imbrication dans A, dans A il y a un élément contenu dans chaque élément de ce nest.
(c) Lemme T yuk et. Chaque famille d'ensembles de caractères finis a un élément maximal.
d) LEMMA KURATOVSKOGO. Chaque chaîne d'un ensemble (partiellement) ordonné est contenue dans une chaîne maximale.
(e) Le lemme de Tson. Si chaque chaîne d'un ensemble partiellement ordonné est bornée au-dessus, alors cet ensemble a un élément maximal.
(f) A à s et o m et un choix. Soit Xα un ensemble non vide pour tout élément a de l'ensemble d'indices A. Alors il existe une fonction c sur A telle que c (a) ∊ Xα pour chaque a de A.
(g) Postulez Tserm elo. Pour toute famille A d'ensembles non vides disjoints, il existe un ensemble C tel que AUC pour chaque A de A se compose exactement d'un point.
(h) IMPRESSIONS et P dans l'ordre complet de livraison. Chaque ensemble peut être entièrement commandé.