Filipp Titarenko, chef de produit pour Femap, Nanosoft JSC
Introduction, ou pourquoi et le sujet de cet article
Tous les ingénieurs ne savent pas comment résoudre les problèmes d'analyse non linéaire. Et pour beaucoup, même parmi ceux qui se spécialisent dans les calculs dans les programmes d'analyse par éléments finis, l'expression "analyse non linéaire" est trompeuse, voire effrayante. Ceux qui ont essayé de résoudre de tels problèmes en passant rappellent des fenêtres avec un grand nombre de paramètres et des graphiques qui se déplacent quelque part et en même temps quelque chose "ne converge pas" (Fig. 1). Cependant, non seulement les problèmes scientifiques, mais aussi les normes et standards d'ingénierie modernes nécessitent souvent de prendre en compte la non-linéarité dans les modèles de calcul. De plus, ces exigences n'existent pas seulement dans les secteurs de l'espace, de l'aviation et de l'ingénierie. Ainsi, par exemple, l'ensemble des règles de la coentreprise 385.1325800.2018 «Protection des bâtiments et des structures contre l'effondrement progressif» lors de la réalisation des calculs nécessite de prendre en compte la non-linéarité géométrique et physique (plasticité, fluage, etc.).

Image 1
Les statistiques d'aujourd'hui sont telles qu'environ 90% des calculs reposent sur une analyse linéaire. D'un point de vue économique, l'analyse linéaire est rapide, simple et bon marché. Mais si vous avez besoin de calculer la réponse à l'impact des chocs, de prendre en compte les effets d'inertie, de suivre l'évolution de la température ou d'autres paramètres au fil du temps, de prendre en compte la présence de surfaces de contact, de non-linéarités géométriques ou de mécanismes complexes de comportement des matériaux, vous ne pouvez pas vous passer d'une analyse non linéaire et de la possibilité de configurer correctement le solveur. Les principaux types de non-linéarité sont géométriques physiques et dus à la présence de surfaces de contact.
Sur le Runet (et dans le réseau mondial), il existe deux types conditionnels de matériel pédagogique sur le thème de l'analyse par éléments finis non linéaires: 1) des instructions pas trop longues sur où et dans quelle séquence cliquer dans votre système de CAO pour calculer votre «poutre, chauffage, support, current ... ", ou 2) de gros manuels universitaires / articles scientifiques ou des manuels d'utilisation de plusieurs pages qui peuvent et devraient être étudiés pendant longtemps ... mais dans les jours et les semaines à venir, il est peu probable qu'il soit possible de calculer quelque chose par vous-même.
Cet article est une tentative de l'auteur, à l'aide d'un exemple spécifique dans un système CAO spécifique, d'illustrer l'algorithme de réalisation d'une analyse statique non linéaire de zéro à l'analyse de la solution, tout en offrant quelques explications sur les fondements théoriques associés aux paramètres du solveur.
Nous allons résoudre le problème du pré-postprocesseur Femap avec le solveur NX Nastran, qui a prouvé sa fiabilité, sa précision et sa vitesse depuis le milieu des années 70 du siècle dernier. J'utilise Femap 2020.2, mais en général, l'algorithme pour résoudre ce type de problèmes est identique non seulement dans les versions précédentes de Femap, mais aussi dans d'autres complexes de calcul FE.
Sur quoi allons-nous nous entraîner? Analyse statique non linéaire
Non, contrairement au héros de la vieille comédie (fig. 2), nous ne nous entraînerons pas sur les chats.

Figure 2
Nous devons calculer le support en forme de L au-delà de la limite d'élasticité de l'acier. Un véritable prototype du support peut être un boulon d'escalade, un support sur l'ISS, ou un élément d'une façade ventilée à charnière. Je l'ai choisi parce que, d'une part, je ne voulais pas prendre le modèle fini, et d'autre part, ce serait bien de ne pas passer beaucoup de temps au lecteur sur le processus de création de la géométrie. Du point de vue du modèle, tout sera aussi simple que possible, je porterai plus d'attention aux paramètres de la théorie et du solveur. Avec cette approche, le lecteur aura la possibilité de répéter indépendamment tout le processus - de la création d'un modèle à son analyse numérique. Et même mener une expérience naturelle.
Lors de la préparation de l'article, j'ai découvert chez moi un support similaire, mais perforé (Fig. 3), que j'avais précédemment retiré avec une pince au-delà de la limite d'élasticité - mais avec des conditions limites différentes pour la fixation. Et à d'autres fins - pas scientifiques et expérimentales, mais à des fins domestiques ...
Figure 3
Mais si vous le souhaitez, vous pouvez toujours vérifier votre expérience numérique: de telles parenthèses sont disponibles dans toutes les quincailleries.
Un peu de théorie: les différences entre l'analyse linéaire et non linéaire
Pour la pratique de la résolution de problèmes d'ingénierie du point de vue des algorithmes de calcul internes, il est important de réaliser que dans l'analyse non linéaire, les charges sont appliquées progressivement et en fait, le solveur résout de manière cohérente de nombreux problèmes. Dans l'analyse statique linéaire, une seule étape est toujours franchie: de l'état initial à l'état final. Lors de la résolution d'un problème non linéaire, toutes les charges spécifiées ne seront pas appliquées immédiatement au corps.
Les données initiales pour chaque étape suivante de l'analyse non linéaire sont l'état du modèle à l'étape précédente. De plus, à chaque étape, les forces internes et externes (paramètres énergétiques) doivent être équilibrées en tenant compte d'une certaine erreur (Fig. 4). Le montant de l'erreur tolérée est déterminé par le critère des tolérances de convergence. En règle générale, ce critère est défini sous forme de pourcentage de la charge appliquée, la charge faisant référence à toutes les forces externes appliquées au modèle ou, dans le cas d'un chargement de déplacement, aux forces de réaction. L'abondance des paramètres s'explique par la complexité des algorithmes de calcul accompagnant l'analyse non linéaire. La valeur typique du critère de convergence de force est comprise entre 0,1 et 1% de la charge appliquée. En recherchant la convergence à une étape de la solution, le programme peut effectuer de nombreuses itérations.Pour ces raisons, la résolution de problèmes non linéaires prend beaucoup plus de temps à l'ordinateur que la résolution de problèmes statiques linéaires. Il est important de comprendre que l'approche en plusieurs étapes peut, pour diverses raisons (types de non-linéarités), nécessiter des problèmes, résultat d'une résolution qui ne dépend pas du temps.
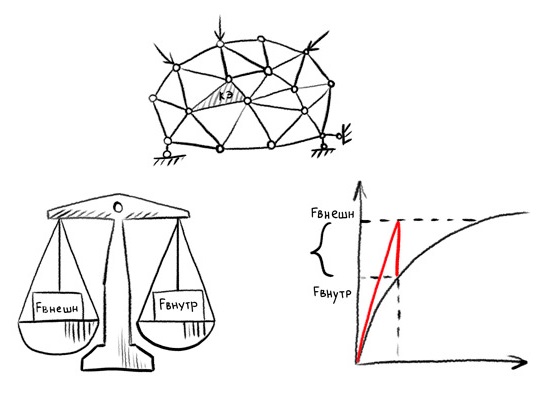
Figure 4
L'exemple le plus simple sur lequel cet énoncé peut être compris est le chargement d'une structure élastique-plastique avec une charge à laquelle la contrainte dépasse la limite d'élasticité. Le solveur «ne sait pas» à l'avance à quelle charge la contrainte dans les nœuds individuels du modèle dépassera cette limite et, par conséquent, les paramètres des équations décrivant l'état de contrainte-déformation du corps changeront fondamentalement. Dans ce cas, à chaque étape de l'incrément de force, il est nécessaire de prendre en compte l'évolution de la zone de déformation plastique. Par conséquent, la solution passe par de nombreuses étapes de l'incrément de charge, et les étapes, à leur tour, si nécessaire, sont effectuées pour un certain nombre d'itérations. Les calculs de la matrice de rigidité peuvent être répétés à chaque étape de la solution. La fréquence de recalcul de la matrice de rigidité est fixée par l'utilisateur. La plasticité est la non-linéarité physique.
En raison du processus «multi-étapes» et «itératif» de la solution, je recommande de maîtriser l'onglet Historique non linéaire, accessible en exécutant le solveur. Dans celui-ci, vous pouvez suivre le nombre d'itérations effectuées et le niveau de la charge atteinte (facteur de charge) en temps réel selon le calendrier. À partir de ce graphique, vous pouvez analyser le taux de convergence de la solution. En cas de problème, le solveur interrompra le processus de résolution et affichera un message indiquant que la solution ne converge pas.
L'analyse linéaire ne peut être utilisée que pour analyser des modèles avec des matériaux linéaires, à condition qu'il n'y ait pas d'autres types de non-linéarités. Les matériaux linéaires peuvent être isotropes, orthotropes ou anisotropes. Si le matériau du modèle a des caractéristiques contrainte-déformation non linéaires sous une charge donnée, une analyse non linéaire doit être utilisée. Différents types de modèles de matériaux peuvent être utilisés dans l'analyse non linéaire.
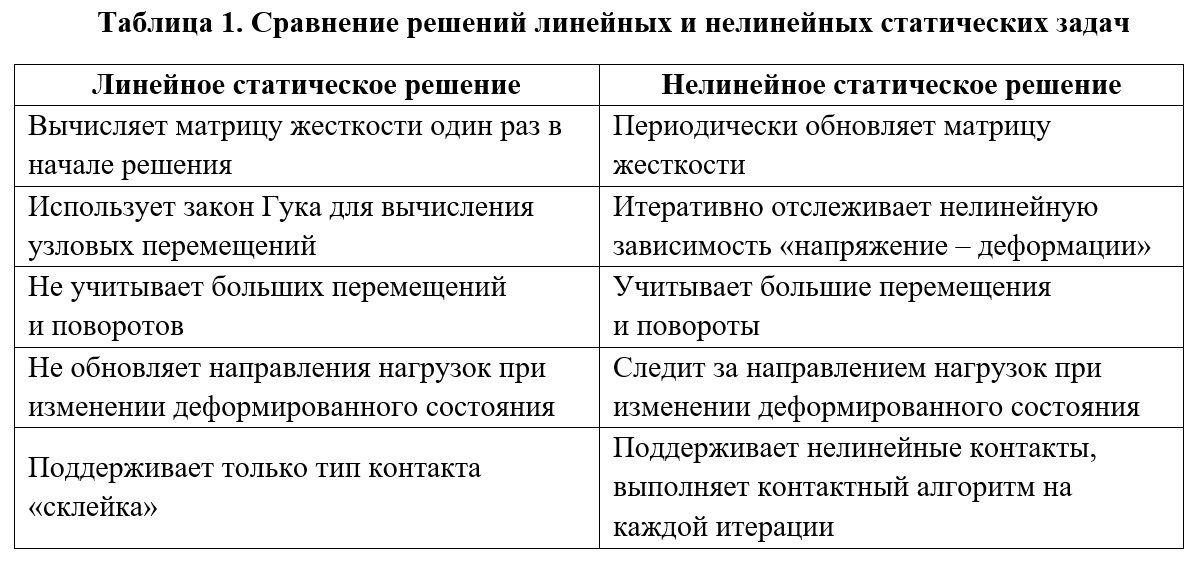
Dans l'analyse statique non linéaire, les phénomènes dynamiques tels que les forces d'inertie et les forces d'amortissement ne sont pas pris en compte. Le traitement d'une solution statique non linéaire diffère du traitement d'une solution statique linéaire en plusieurs points principaux, présentés dans le tableau. 1.
La théorie générale suffit pour cela, mais j'écrirai ci-dessous sur la façon de configurer les algorithmes pour résoudre le système non linéaire global d'équations algébriques généré par la méthode des éléments finis, lorsque nous arrivons à l'endroit approprié lors de l'analyse de notre exemple pratique avec une parenthèse. Dans Femap, la plupart de ces paramètres se trouvent dans la boîte de dialogue Nastran Nonlinear Analysis, accessible à partir de la boîte de dialogue Analysis Set en définissant 10..Nonlinear Static dans le champ Analysis Type et en cliquant plusieurs fois sur Next. Mais tout a son temps.
Mise en route: modélisation de parenthèses et analyse linéaire dans Femap avec NX Nastran
Dans le menu de commande, ouvrez l'onglet Fichier → Préférences → Géométrie / Modèle. Dans les paramètres Facteur d'échelle de la géométrie solide, définissez Mètres, qui correspond au système SI de mesures de grandeurs physiques.
Notre support en forme de L sera composé de deux plaques carrées avec des côtés de 0,1 mètre, situées dans des plans perpendiculaires. Dans le menu de commande, allez dans Géométrie → Surface → Coins et créez successivement deux plaques carrées.
1) Les coordonnées des sommets de la première plaque: 1) X = 0; Y = 0; Z = 0; 2) X = 0,1; Y = 0; Z = 0; 3) X = 0,1; Y = 0; Z = 0,1; 4) X = 0; Y = 0; Z = 0,1.
2) Pour le second: 1) X = 0; Y = 0; Z = 0; 2) X = 0; Y = 0,1; Z = 0; 3) X = 0; Y = 0,1; Z = 0,1; 4) X = 0; Y = 0; Z = 0,1.
En conduisant séquentiellement ces points dans la boîte de dialogue Localiser → Entrer № Coin de la surface, nous obtiendrons la géométrie souhaitée. En appuyant sur Ctrl + A, nous pouvons afficher notre géométrie au centre de la fenêtre à une échelle appropriée.
Ensuite, nous allons créer le matériau de nos plaques (Acier 3) et définir ses propriétés. Pour ce faire, dans le panneau Informations sur le modèle situé sur le côté gauche de l'écran, ouvrez l'onglet Modèle, puis cliquez avec le bouton droit sur la ligne Matériaux et cliquez sur Nouveau. La boîte de dialogue Define Material - ISOTROPIC s'ouvre. Dans le champ Titre, saisissez le nom St3. Dans le champ Général, définissez le module de Young, E = 2e11, le rapport de Poisson, nu = 0,3, la densité de masse = 7850. Nous n'irons pas dans l'onglet Non linéaire pour le moment. Cliquez sur OK puis sur Annuler.
Créons un type d'élément final et spécifions ses propriétés. Pour ce faire, dans l'onglet Modèle, cliquez avec le bouton droit sur la ligne Propriétés et cliquez sur Nouveau. La boîte de dialogue Définir la propriété - Type d'élément de plaque s'ouvre. Dans le champ Titre, entrez le nom Pl0005. Dans l'onglet Matériau, sélectionnez 1..St3. Cliquez ensuite sur le bouton Elem / Property Type et assurez-vous que la case à cocher est au bon endroit: Éléments de plan - Plaque. Autrement dit, un élément fini plat est sélectionné - une plaque. Définissons l'épaisseur de la plaque, pour cela, dans le champ Epaisseurs, définissons TavgorT1 = 0,005. Cliquez sur OK puis sur Annuler.
Sauvegardons notre modèle, pour lequel nous appuyons sur Fichier → Enregistrer sous, sélectionnez le chemin pour enregistrer le fichier et le nom du fichier. Je l'appellerai KronNonlin.
Définissons les propriétés de maillage du modèle d'éléments finis. Pour ce faire, dans le menu des commandes, cliquez sur Maillage → Contrôle du maillage → Taille sur surface. Dans la boîte de dialogue Sélection d'entité → Sélectionner la ou les surfaces pour définir la taille de maillage, cliquez sur Sélectionner tout pour sélectionner toutes les surfaces. En cliquant sur OK, nous entrons dans la boîte de dialogue Dimensionnement automatique du maillage. Dans le champ Taille de l'élément, définissez la valeur 0,005 et cliquez sur OK. Désormais, la dimension caractéristique de nos éléments finis sera de 5 mm. Des points sont apparus sur les lignes du modèle, nous donnant des informations sur la taille des éléments après la création des éléments finis.
Créons maintenant un modèle d'éléments finis. Dans le menu de commandes, cliquez sur Maillage → Géométrie → Surface. Dans la boîte de dialogue Sélection d'entités → Sélectionner les surfaces à mailler, cliquez sur Sélectionner tout et OK. Dans le champ Propriété, définissez le type FE que nous avons créé 1..Pl0005 et dans le champ Maillage, cochez la case Quad. Cliquez sur OK. Le modèle d'éléments finis a été créé. Maintenant, nous allons réparer le support et le charger avec des forces externes.
Nous fixerons le support pour quatre nœuds (une telle fixation correspond le plus étroitement à la fixation avec des rivets ou au soudage par points) le long de six degrés de liberté, et le long de la ligne du joint de deux plaques - le long de trois degrés de liberté (laissant la possibilité de rotation autour de la ligne).
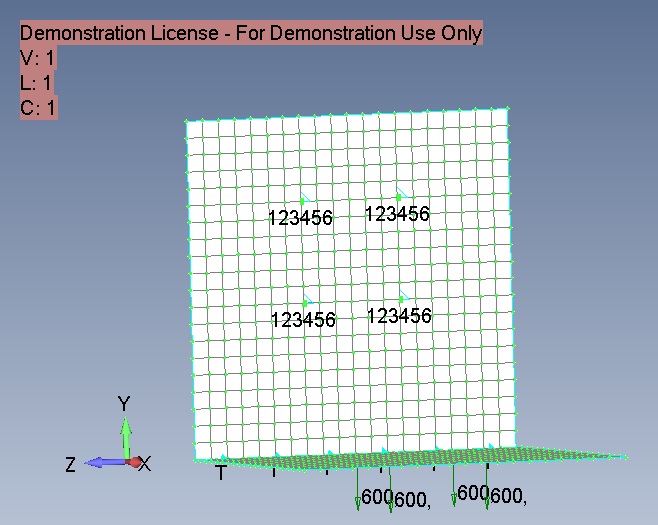
Figure 5
Nous fixons les conditions limites pour la fixation. Pour ce faire, faites un clic droit sur Contraintes, cliquez sur Nouveau et entrez le nom Constr. Ensuite, cliquez avec le bouton droit sur Définitions de contraintes et sélectionnez Nœuds. Sélection de quatre nœuds comme indiqué sur la fig. 5, nous les fixons à six degrés de liberté; cliquez sur OK. Dans le champ Titre de la boîte de dialogue Créer des contraintes nodales / DOF, écrivez 4 nœuds et cliquez sur le bouton Fixe pour contraindre le mouvement-rotation. Cliquez sur OK. Cliquez à nouveau avec le bouton droit sur Définitions de contraintes et sélectionnez Courbes. Dans le champ Titre de la boîte de dialogue Créer des contraintes sur la géométrie, spécifiez Ligne et cliquez sur le bouton Epinglé - Pas de translation pour contraindre le mouvement, laissant la possibilité de rotation.
Définissons les conditions de chargement en faisant un clic droit sur Charges - Nouveau. Le nouvel ensemble s'appellera Vert. Cliquez avec le bouton droit sur Définitions de charge - Nodal et sélectionnez quatre nœuds auxquels les données de charge seront appliquées. Dans la boîte de dialogue Créer Loadson Nodal, nommons notre charge Force600. Les forces nodales sont dirigées le long de l'axe Y dans une direction négative. La valeur de la charge nodale FY est de moins 600 Newton. Ainsi, une charge de 600 Newtons sera appliquée à chacun des quatre nœuds (soit 240 kg pour les quatre nœuds).
Ensuite, passons aux paramètres d'analyse. Dans le menu de commandes, choisissez Modèle → Analyses. Appuyez sur le bouton Nouveau pour sélectionner le type d'analyse et le solveur. Dans le champ Titre, saisissez Linear. Nous sélectionnons le programme d'analyse - 36..Simcenter Nastran et type d'analyse 1..Static. Ensuite, en appuyant sur le bouton Analyser, nous commençons le calcul. La solution me prend moins d'une seconde (!). Femap nous montre une fenêtre d'observation des résultats d'analyse: Simcenter Nastran Analysis Monitor. Analyse terminée 0 signifie que l'analyse a été effectuée avec succès.
Dans Info modèle, faites un clic droit sur Résultats → Tous les résultats → Déformer. Maintenant, nous voyons l'état déformé de notre support sous une forme exagérée. À mon avis, l'état déformé est visuellement exagéré, alors appuyez sur F6: la boîte de dialogue des options d'affichage s'ouvre. Allons à l'onglet Post-traitement, Style déformé dans le champ Echelle, définissez 4%. La visualisation de l'état déformé du modèle est désormais moins exagérée. Les déplacements maximaux peuvent être visualisés dans le coin inférieur gauche du modèle - ils sont de 0,0026 m.
Appuyez sur la touche F5 et affichez la distribution des contraintes dans le modèle. Dans le champ Style de contour, cochez la case Contour, puis cliquez sur le bouton Données déformées et de contour. Dans l'onglet Contour, sélectionnez 7033 Plate Top Von Mises Stress pour que Femap affiche les contraintes aux nœuds. Notre modèle est devenu multicolore, les couleurs reflètent le niveau de tension (Fig. 6). Sur le côté droit de l'écran, on voit une échelle indiquant quelle couleur correspond à quel niveau de tension. Pour masquer le modèle géométrique d'origine, cliquez sur l'icône Afficher les surfaces bascule. Les contraintes maximales atteignent 332,4 MPa, ce qui est nettement supérieur à la limite d'élasticité de 210 MPa pour l'acier St3.
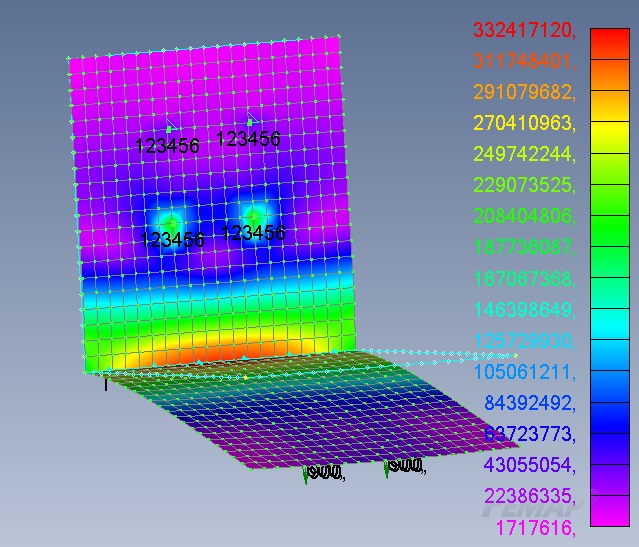
Graphique 6
Ainsi, les contraintes aux points de la parenthèse sont beaucoup plus élevées que la limite d'élasticité. L'analyse linéaire ne prend pas en compte la fluidité-plasticité des matériaux et l'effet de redistribution des contraintes associé à ce phénomène, donc cette répartition des contraintes ne correspond pas à la réalité. Passons à l'analyse non linéaire.
Pratique: Analyse statique non linéaire dans Femap avec NX Nastran
Pour passer d'un modèle linéaire à un modèle non linéaire, nous devons effectuer juste quelques actions (nous ne changeons pas la partition, les conditions de fixation et de chargement).
Modifiez les propriétés du matériau en ajoutant des déformations plastiques; pour ce faire, dans l'onglet Matériaux, faites un clic droit sur notre matériau 1 ... St3 et appuyez sur Modifier. Allons à l'onglet Non linéaire et sélectionnez Plastique dans le champ Type de non-linéarité. Dans le champ Critère de rendement, sélectionnez 0..von Mises, dans le champ Contrainte de rendement initiale, saisissez la valeur 210 000 000 (soit 210 MPa). Cliquez sur OK.
NX Nastran prend en charge les critères de ductilité suivants:
- Mises (von Mises) - utilisé pour la matière plastique dans la plupart des cas;
- Morue (Tresca) - pour les matériaux fragiles et certains matériaux ductiles;
- Drucker-Prager - pour les matériaux tels que le sol et le béton avec friction interne;
- - (Mohr-Coulomb) – .
- .
Dans le menu de commandes, sélectionnez Modèle → Analyses. Appuyez sur le bouton Nouveau pour sélectionner le type d'analyse et le solveur. Dans le champ Titre, saisissez Non linéaire1. Nous sélectionnons le programme d'analyse - 36..Simcenter Nastran et Analysis Type 10..Nonlinear Static. Cliquez sur le bouton Suivant. Dans la fenêtre Nastran Executive and Solution Options, cochez la case Number of Processors et entrez le nombre de processeurs sur notre ordinateur. Ensuite, nous appuyons sur le bouton Suivant six fois de suite, sans modifier les paramètres par défaut dans les boîtes de dialogue, jusqu'à ce que nous arrivions à la boîte de dialogue Analyse non linéaire Nastran. Il s'agit de la fenêtre clé pour les paramètres d'analyse non linéaire, nous allons donc nous attarder sur cet endroit plus en détail et examiner ses champs de paramètres (Fig. 7).
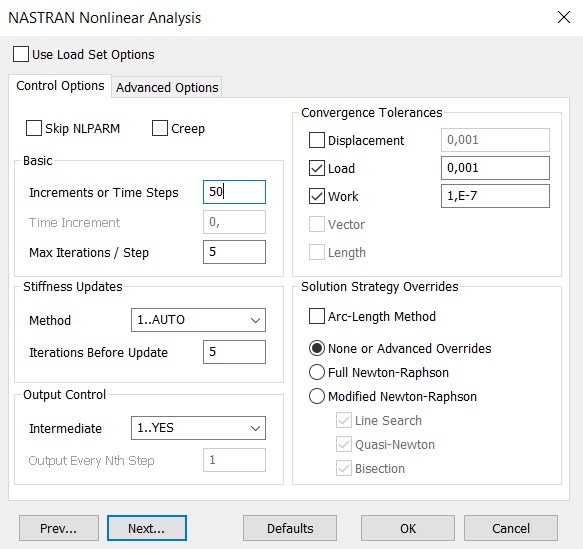
Figure 7
S'il est nécessaire de prendre en compte l'effet du fluage, vérifiez le champ Fluage.
Dans le champ De base, définissez le nombre d'étapes pour augmenter la charge (incréments ou pas de temps) et le nombre maximal d'itérations à chaque étape (itérations / étapes max). Dans le cas d'une analyse statique non linéaire, les incréments ou les pas de temps reflètent le niveau de charge. Dans le graphique Historique non linéaire, qui illustre le nombre d'itérations effectuées en temps réel, le niveau de charge est tracé sur l'axe vertical et est appelé facteur de charge. Sa valeur est comprise entre 0 et 1. Pour un nombre de pas donné, la charge passe de 0 à pleine; dans ce cas, si les conditions de convergence l'exigent, plusieurs itérations sont effectuées en une seule étape. Ces deux paramètres sont très importants, dans chaque tâche, vous devez essayer de choisir un «bon moyen» entre trop de «pas» et «d'itérations» et trop peu. S'il y en a trop peu,alors la solution ne convergera pas ou aura un impact négatif sur la précision. Si leur nombre s'avère excessif, la solution consommera beaucoup de puissance machine, de temps et la convergence peut être affectée négativement. Pour étudier l'influence de ces paramètres, nous résolvons notre problème avec une parenthèse plusieurs fois avec différentes combinaisons du nombre de "pas" et "itérations", tout en observant le graphe de la chronologie non linéaire.tout en observant le graphique de la chronologie non linéaire.tout en observant le graphique de la chronologie non linéaire.
Pour un problème statique non linéaire dans le champ Mises à jour de rigidité, vous pouvez sélectionner l'une des trois méthodes (AUTO, ITER, SEMI) pour mettre à jour la matrice de rigidité du corps, ainsi que le nombre d'itérations (Itération avant la mise à jour) par lesquelles la matrice sera mise à jour. Si la méthode est mal choisie, alors 0..Default (par défaut) sera utilisé automatiquement. Dans la méthode AUTO, la matrice de rigidité est mise à jour à partir des estimations de la convergence de différentes méthodes numériques (quasi-newtonienne, avec itération linéaire, demi-division) et avec le choix de celle qui donnera le nombre minimum de mises à jour de la matrice de rigidité. La méthode SEMI est similaire à la méthode AUTO, mais la matrice de rigidité est nécessairement mise à jour à la première itération après le changement de charge, ce qui est efficace pour les processus hautement non linéaires.La méthode ITER (dans l'analyse temporelle non linéaire, elle est similaire à la méthode TSTEP) met à jour la matrice de rigidité après le nombre d'itérations spécifié dans le champ Itération avant mise à jour. La méthode ITER est efficace pour les processus hautement non linéaires dans lesquels la géométrie du corps change considérablement pendant la déformation (par exemple, lorsque la stabilité est perdue).
Dans le champ Contrôle de sortie, les paramètres de sortie des résultats aux étapes de chargement intermédiaires (pas de temps, si nous parlons d'analyse temporelle) sont définis. Lorsque vous effectuez une analyse non linéaire statique dans l'onglet Intermédiaire, vous pouvez sélectionner l'une des options suivantes: 0..Défaut (par défaut), OUI (affichage), NON (ne pas afficher), Tout (afficher à toutes les étapes). Avec l'analyse non linéaire dans le temps, vous pouvez définir le nombre d'étapes après lesquelles le résultat doit être affiché.
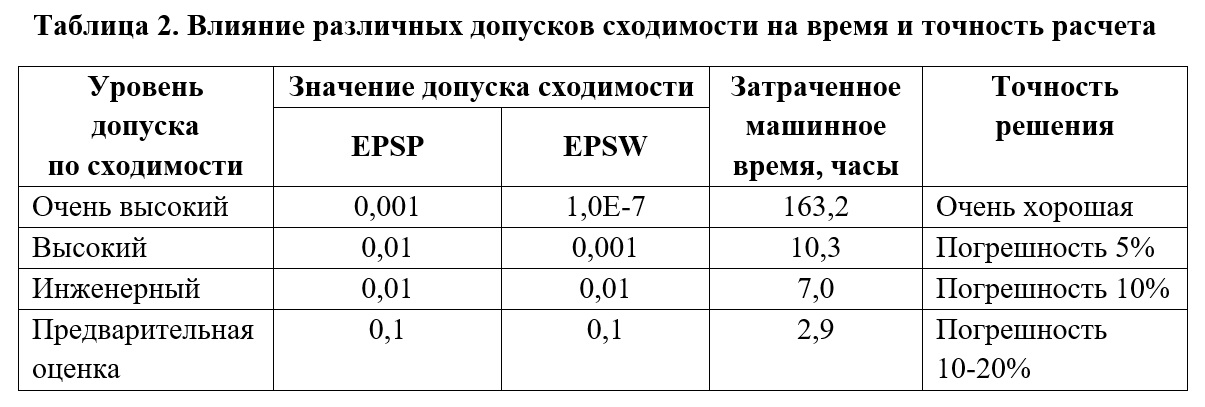
Le champ Tolérance de convergence spécifie les tolérances pour respecter les conditions de convergence pour les charges (charge), les déplacements (déplacement) et le travail interne (travail). Considérons l'influence des tolérances de convergence sur la précision et le temps de résolution du problème à l'aide de l'exemple du modèle étudié par les développeurs de Femap avec NX Nastran de Siemens.
Un très grand modèle non linéaire (950 000 DOF) a été soigneusement examiné pour déterminer l'effet des différentes tolérances des critères de convergence sur le temps d'exécution et la précision des calculs. Il n'y avait aucun transfert de chaleur, espaces ou contacts dans ce modèle. Les résultats de l'étude ont montré qu'une précision acceptable de la solution (par rapport à la solution obtenue avec un niveau de tolérance de convergence très élevé) peut être obtenue aussi bien pour le niveau de tolérance de convergence «élevé» que «d'ingénierie». Le niveau de tolérance de convergence «estimation préliminaire» produit un résultat avec les mêmes tendances générales que les niveaux de tolérance supérieurs, mais les réponses ne sont pas suffisamment précises pour un projet de travail. Avec une diminution du niveau de tolérance pour la convergence, le calcul est beaucoup plus rapide. Table 2, les tendances présentées peuvent être quantifiées.
Dans le champ Remplacements de stratégie de solution, les paramètres du processus de résolution du système non linéaire global d'équations algébriques générées par la méthode des éléments finis sont définis. Pour modifier consciemment ces paramètres, vous devez avoir des connaissances et de l'expérience - s'ils ne suffisent pas, il est préférable de laisser les paramètres par défaut. Voici quelques explications.
La méthode de longueur d'arc définit la valeur du pas de temps (charge supplémentaire), en tenant compte des informations sur le déplacement des nœuds du corps - elle doit être utilisée si la tâche est associée à une forte déformation (perte de stabilité).
La méthode Full Newton-Raphson converge très rapidement, mais il faut plus de temps pour créer une matrice supplémentaire pour la matrice complète du système d'équations algébriques à chaque itération.
La méthode Newton-Raphson modifiée n'a pas besoin de cette action, mais converge beaucoup plus lentement, donc des procédures supplémentaires peuvent être utilisées pour l'accélérer: Recherche de ligne (recherche linéaire), Quasi-Newton (accélération quasi-newtonienne) et / ou Bisection ( demi-division).
Ainsi, nous avons analysé les paramètres de base de l'analyse statique non linéaire (les paramètres de l'analyse non linéaire dans le temps leur sont très similaires). Pour calculer notre parenthèse dans la fenêtre Analyse non linéaire Nastran, définissez les paramètres suivants: dans le champ Incréments ou Pas de temps - 50, Max itérations / étape - 5, Méthode de mise à jour de rigidité - 1..AUTO, Itérations avant mise à jour - 5, Intermédiaire - 1..OUI ... Laissez les autres paramètres inchangés. Cliquez sur OK et accédez à la fenêtre Analysis Set Manager. Pour démarrer le calcul, appuyez sur le bouton Analyser. Femap ouvrira automatiquement la fenêtre Simcenter Nastran Analysis Monitor. Passons à l'onglet Historique non linéaire en déplaçant la case à cocher du journal vers l'historique non linéaire (Fig. 8).
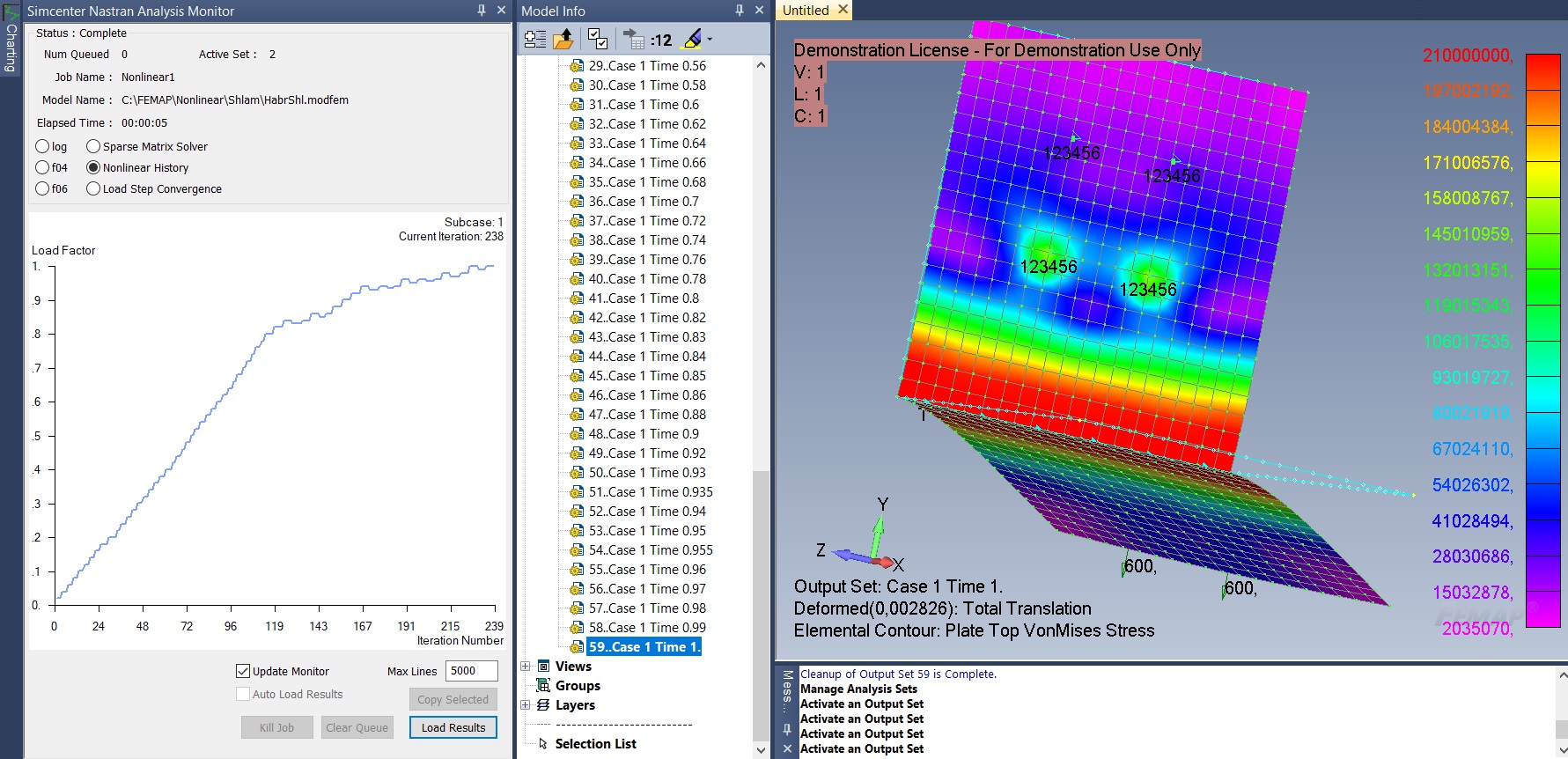
Figure 8
Il affiche un graphique montrant en temps réel le nombre d'itérations effectuées et (dans le cas de notre analyse statique non linéaire) le facteur de charge, c'est-à-dire un facteur de charge de 0 à 1. Dans le coin supérieur droit, nous voyons des informations sur le numéro de l'itération en cours. Veuillez noter qu'il ne s'agit pas du numéro d'étape de l'incrément de charge, mais du numéro de l'itération actuelle. Chaque étape de l'incrément de charge peut contenir plusieurs itérations - cela est nécessaire pour l'exécution d'algorithmes qui implémentent la convergence de la solution. Si l'incrément ne converge pas, cela signifie que le changement de charge est trop important pour passer à l'étape suivante; la charge est réduite - des itérations supplémentaires sont effectuées en une seule étape.
Dans la fenêtre Informations sur le modèle, ouvrez l'onglet Résultats → Tous les résultats. Un double-clic sur la ligne de solution ouvre les résultats à différents niveaux de charge de 0 à 100%. Analysons ensemble le graphique de la chronologie non linéaire et l'état de contrainte-déformation du support à différents niveaux de charge.
À un niveau de charge de 0 à 0,62 (facteur de charge), la contrainte est inférieure à la limite d'élasticité de 210 MPa, après quoi la déformation plastique de l'acier du support commence. L'unité 1 correspond à une charge totale appliquée de 240 kg pour quatre nœuds. Les contraintes maximales sont surlignées en rouge - elles sont concentrées près de la ligne d'intersection des surfaces. À un niveau de charge de 0,62 à 1, la zone de déformation plastique augmente - les contraintes maximales (contrairement à l'analyse linéaire) n'augmentent pas. Avec un facteur de charge de 0,82, le taux de croissance de la courbe diminue, ce qui signifie que plus d'itérations sont nécessaires pour chaque étape pour satisfaire les conditions de convergence. Nous avons pu atteindre la pleine charge 1 - le déplacement maximal était de 0,00283 m. Dans certains cas (par exemple,si nous augmentons considérablement la charge), la géométrie du corps déformé est tellement déformée que la convergence ne peut pas être obtenue avec cette stratégie (paramètres du solveur). Comme vous pouvez le voir, les résultats de l'analyse non linéaire sont qualitativement et quantitativement différents des résultats de l'analyse linéaire.
Faisons trois autres calculs, définissant des paramètres différents pour le nombre d'étapes d'incréments et d'itérations (Fig. 9). Dans le premier cas, les incréments ou pas de temps - 50, max itérations / pas - 5.
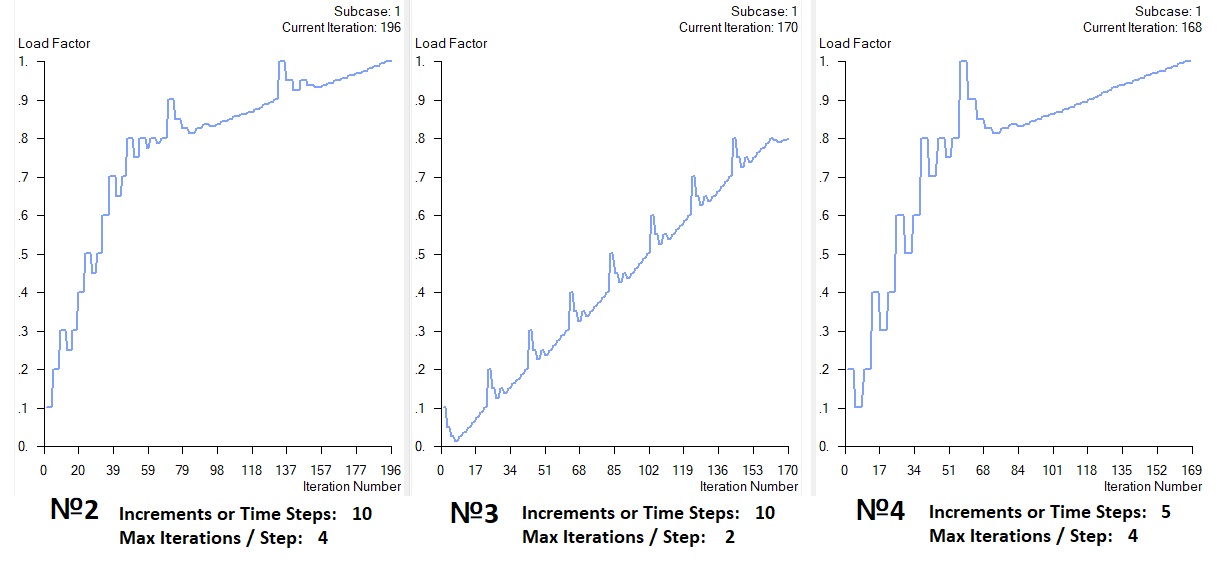
Figure 9
Les conditions de convergence ont été remplies dans les 1er, 2e et 4e cas de calcul. Dans le 3ème cas de conception, une erreur fatale avec l'explication que la solution ne converge pas est apparue à un niveau de charge de 0,8. Notez que dans les 2ème et 4ème calculs, la solution a été réalisée avec succès (pleine charge 1) avec un nombre significativement plus petit d'étapes et d'itérations. Notre modèle est assez simple et tous les calculs ont été effectués en moins de 5 secondes. Sur les grands modèles, il est possible de gagner beaucoup de temps machine en choisissant le bon nombre d'incréments et d'itérations de charge.
Conclusion
De nombreuses questions restent en dehors du cadre de cet article: chargement multi-étapes (application de cas et sous-cas), application de contacts non linéaires, analyse non linéaire dans le temps, actions dans les cas où la solution "s'effondre". Mais j'espère que l'objectif principal de l'article a été atteint - les lecteurs qui n'ont pas une vaste expérience dans la résolution de problèmes non linéaires ont maintenant un ensemble minimum de connaissances théoriques et d'images pratiques pour se lancer dans l'analyse par éléments finis non linéaires.
Littérature
- Guide de l'utilisateur de l'analyse non linéaire de base. Siemens.
- Rudakov K.N. Femap 10.2.0. Modélisation géométrique et par éléments finis des structures. K.: KPI, 2011 .-- 317 p., Ill.
Philip Titarenko,
Product Manager pour Femap
, Nanosoft JSC
E-mail: titarenko@nanocad.ru
Chers lecteurs, je vous invite à trois événements intéressants et utiles qui auront lieu dans un proche avenir:
- Le 20 août, j'organise un webinaire gratuit " Analyse non linéaire dans Femap avec NX Nastran ".
- Le 17 septembre, je vous attends au webinaire "Tâches de contact dans Femap avec NX Nastran". Un lien vers celui-ci apparaîtra dans les prochains jours dans la section événements .
Lors des webinaires, je serai heureux de répondre à vos questions. - Le Symposium Femap 2020 se tiendra les 9 et 10 septembre, au cours duquel des spécialistes des entreprises industrielles russes et des développeurs Femap de Siemens partageront leur expérience et leurs compétences en ingénierie dans le domaine de la modélisation par éléments finis. Pour en savoir plus sur le symposium, suivez le lien .
Une version d'essai gratuite de Femap avec NX Nastran peut être téléchargée ici .