Pour la génétique du blé, une tâche importante est de déterminer la ploïdie (le nombre d'ensembles identiques de chromosomes dans le noyau cellulaire). L'approche classique pour résoudre ce problème est basée sur l'utilisation de méthodes de génétique moléculaire, qui sont coûteuses et demandent beaucoup de travail. La détermination des types de plantes n'est possible que dans des conditions de laboratoire. Par conséquent, dans ce travail, nous testons l'hypothèse: est-il possible de déterminer la ploïdie du blé à l'aide de méthodes de vision par ordinateur, uniquement sur la base d'une image d'une oreille.

Description des données
Pour résoudre le problème, avant même le début de l'atelier, un ensemble de données a été préparé dans lequel la ploïdie était connue pour chaque espèce végétale. Au total, nous avions 2344 photographies d'hexaploïdes et 1259 tétraproïdes à notre disposition.
La plupart des plantes ont été photographiées en utilisant deux protocoles. Le premier cas - sur une table en une projection, le second - sur une pince à linge en 4 projections. Les photographies avaient toujours une palette de couleurs de vérificateur de couleurs , il est nécessaire de normaliser les couleurs et de déterminer l'échelle.

Un total de 3603 photos avec 644 numéros de graines uniques. L'ensemble de données contient 20 espèces de blé: 10 hexaploïdes, 10 tétraploïdes; 496 génotypes uniques; 10 végétation unique. Les plantes ont été cultivées entre 2015 et 2018 dans des serresICG SB RAS . Le matériel biologique a été fourni par l'académicien Nikolai Petrovich Gontcharov .
Validation
Une plante de notre ensemble de données peut correspondre à jusqu'à 5 photographies prises en utilisant différents protocoles et dans différentes projections. Nous avons divisé les données en 3 ensembles stratifiés: train (échantillon d'apprentissage), valide (échantillon de validation) et attente (échantillon retardé), dans des ratios de 60%, 20% et 20%, respectivement. Lors de la division, nous avons tenu compte du fait que toutes les photographies d'un certain génotype apparaissaient toujours dans un sous-échantillon. Ce schéma de validation a été utilisé pour tous les modèles formés.
Essayer les méthodes classiques de CV et ML
La première approche que nous avons utilisée pour résoudre le problème est basée sur l'algorithme existant que nous avons développé précédemment. L'algorithme permet d'extraire un ensemble fixe de différentes caractéristiques quantitatives de chaque image. Par exemple, la longueur de l'oreille, la zone des arêtes , etc. Pour une description détaillée de l'algorithme, voir Genaev et al., Morphometry of the Wheat Spike by Analyzing 2D Images, 2019 . En utilisant cet algorithme et des méthodes d'apprentissage automatique, nous avons formé plusieurs modèles pour prédire les types de ploïdie.
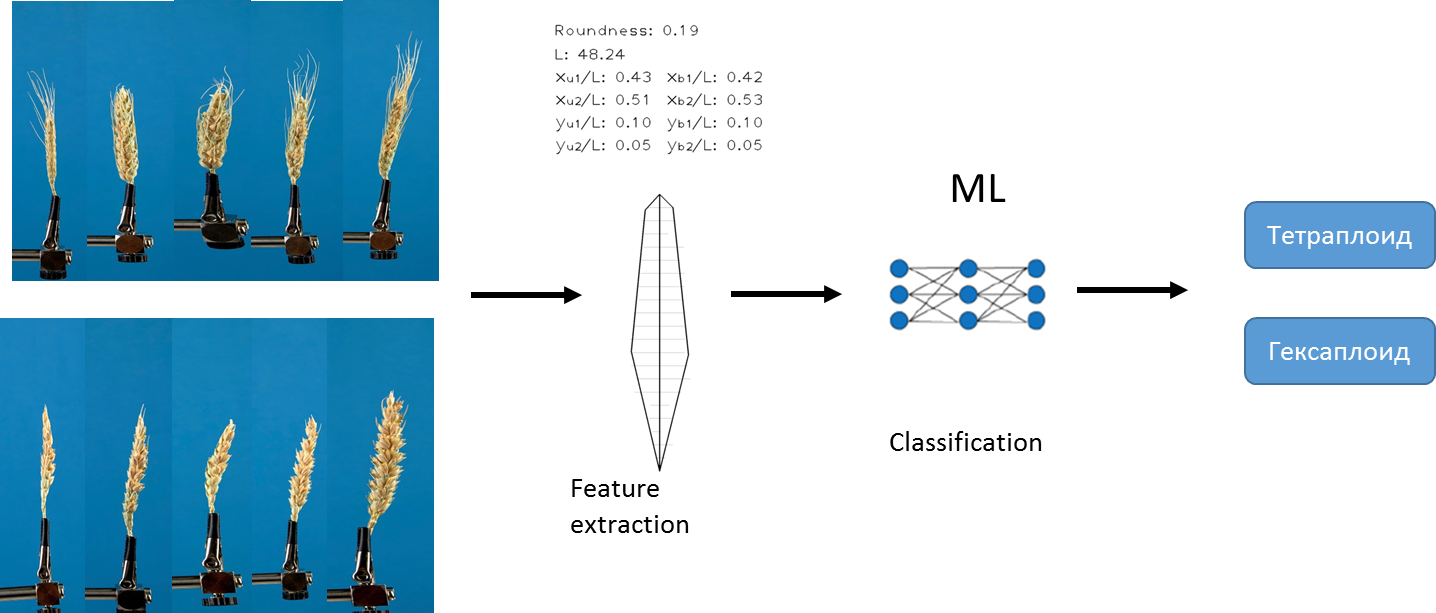
Nous avons utilisé des méthodes de régression logistique , des forêts aléatoires et un renforcement de gradient . Les données ont été pré - normalisé... Nous avons choisi l' AUC comme mesure d'exactitude .
| Méthode | Train | Valide | Résistant |
| Régression logistique | 0,77 | 0,70 | 0,72 |
| Forêt aléatoire | 1,00 | 0,83 | 0,82 |
| Booster | 0,99 | 0,83 | 0,85 |
La meilleure précision sur l'échantillonnage différé a été montrée par la méthode d'amplification de gradient; nous avons utilisé l'implémentation CatBoost.
Interpréter les résultats
Pour chaque modèle, nous avons reçu une estimation de «l'importance» de chaque trait. En conséquence, nous avons obtenu une liste de toutes nos fonctionnalités, classées par importance et sélectionné les 10 principales fonctionnalités: zone des aubes, indice de circularité, rondeur, périmètre, longueur de la tige, xu2, L, xb2, yu2, ybm. (une description de chaque fonctionnalité peut être trouvée ici ).
Un exemple de traits importants est la longueur et le périmètre des oreilles. Les distributions des valeurs de ces traits chez les tétraploïdes et les hexaploïdes sont indiquées sur les histogrammes. On peut voir que la distribution des hexaploïdes est déplacée vers des valeurs plus élevées.

Nous avons regroupé les 10 principales fonctionnalités à l'aide de la méthode t-SNE
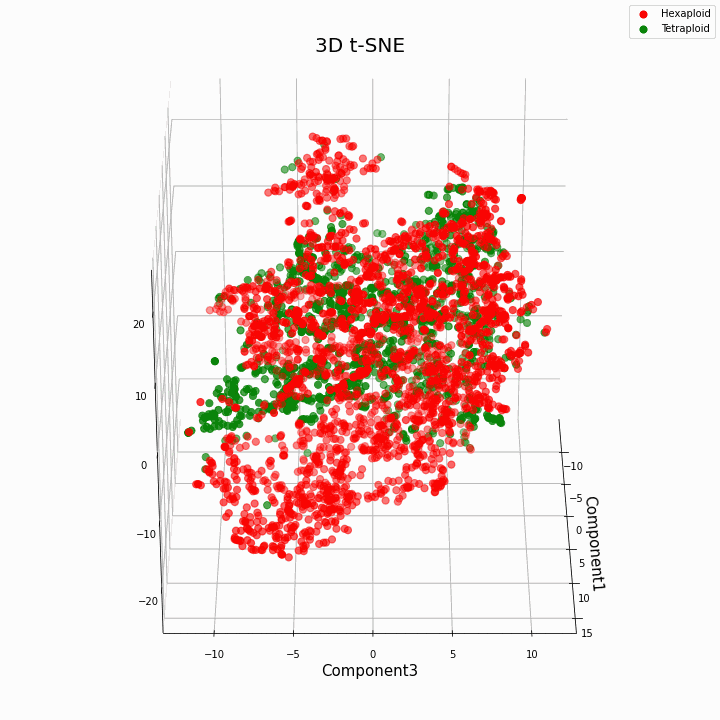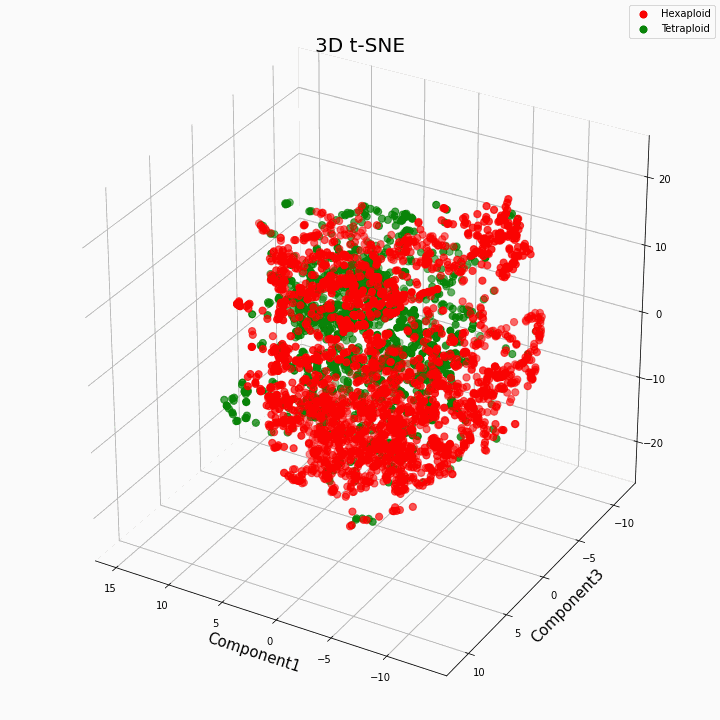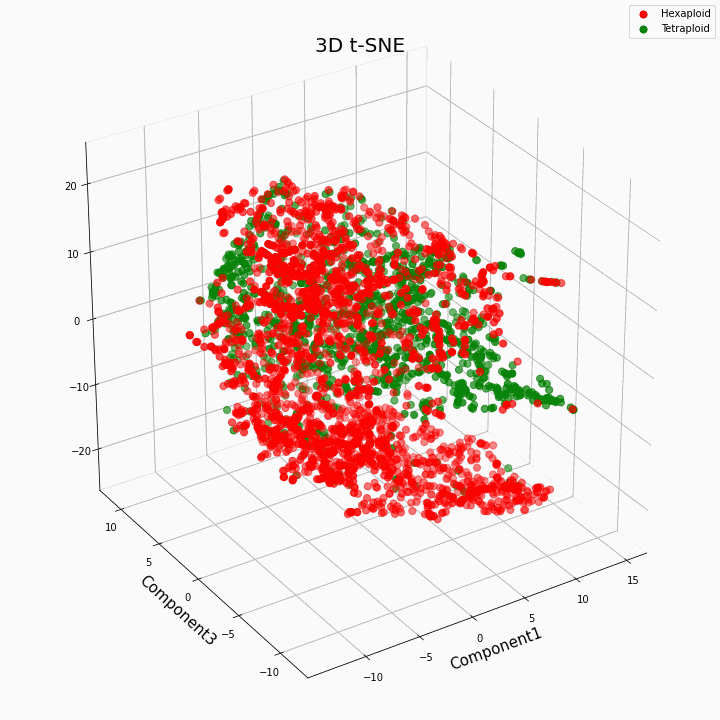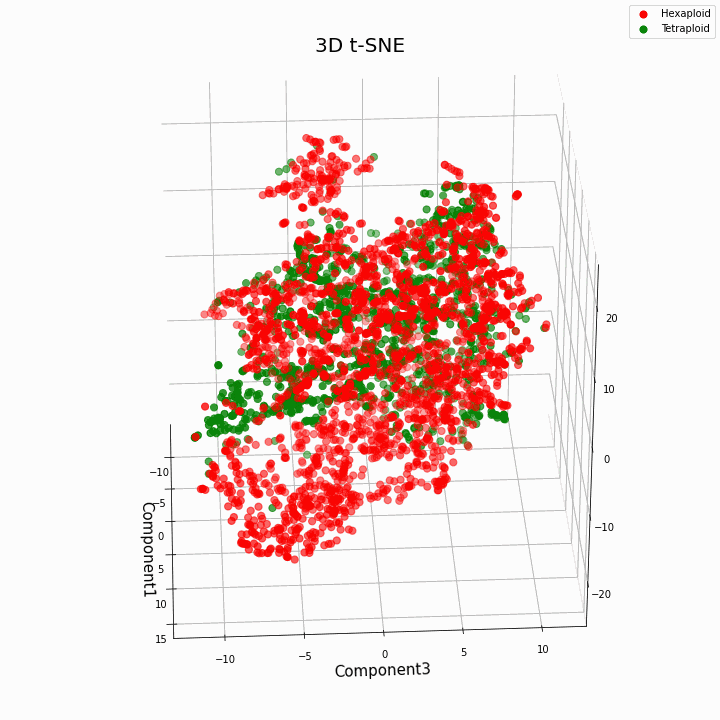
En général, une plus grande ploïdie donne des valeurs de caractères plus variables. Pour les hexaploïdes, une plus grande dispersion / variance des valeurs du trait est caractéristique. En effet, le nombre de copies de gènes dans les hexaploïdes est plus grand et donc le nombre de variantes du «travail» de ces gènes augmente.
Pour confirmer notre hypothèse d'une plus grande variabilité phénotypique dans les hexaploïdes, nous avons appliqué la statistique F. La statistique F donne la signification des différences dans les variances des deux distributions. Nous avons considéré les cas où la valeur p est inférieure à 0,05 pour réfuter l'hypothèse nulle selon laquelle il n'y a pas de différences entre les deux distributions. Nous avons effectué ce test indépendamment pour chaque trait. Conditions de test: il doit y avoir un échantillon d'observations indépendantes (dans le cas de plusieurs images, ce n'est pas le cas) et de distributions normales. Pour remplir ces conditions, nous avons testé une image de chaque oreille. Ils n'ont pris des photographies qu'en une seule projection selon le protocole «sur la table». Les résultats sont présentés dans le tableau. On peut voir que la variance pour les hexaploïdes et les tétraploïdes présente des différences significatives pour 7 caractères. De plus, dans tous les cas, la valeur de dispersion est plus élevée dans les hexaploïdes.La plus grande variabilité phénotypique des hexaploïdes peut être expliquée par le grand nombre de copies d'un gène.
| Name | F-statistic | p-value | Disp Hexaploid | Disp Tetraploid |
| Awns area | 0.376 | 1.000 | 1.415 | 3.763 |
| Circularity index | 1.188 | 0.065 | 0.959 | 0.807 |
| Roundness | 1.828 | 0.000 | 1.312 | 0.718 |
| Perimeter | 1.570 | 0.000 | 1.080 | 0.688 |
| Stem length | 3.500 | 0.000 | 1.320 | 0.377 |
| xu2 | 3.928 | 0.000 | 1.336 | 0.340 |
| L | 3.500 | 0.000 | 1.320 | 0.377 |
| xb2 | 4.437 | 0.000 | 1.331 | 0.300 |
| yu2 | 4.275 | 0.000 | 2.491 | 0.583 |
| ybm | 1.081 | 0.248 | 0.695 | 0.643 |
Nos données comprennent 20 espèces de plantes. 10 blé hexaploïdes et 10 tétraploïdes.
Nous avons coloré les résultats du regroupement afin que la couleur + la forme de chaque point corresponde à une vue spécifique.

La plupart des espèces occupent des zones assez compactes sur la carte. Ces domaines peuvent cependant se chevaucher beaucoup avec d'autres. D'autre part, au sein d'une même espèce, il peut y avoir des groupes clairement définis, par exemple pour T compactum, T petropavlovskyi.
Nous avons fait la moyenne des valeurs de chaque espèce pour 10 caractéristiques, obtenant un tableau de 20 par 10. Où chacune des 20 espèces correspond à un vecteur de 10 caractéristiques. Pour ces données, une matrice de corrélation a été construite et une analyse de cluster hiérarchique a été effectuée. Les carrés bleus du graphique correspondent aux tétraploïdes.

Sur l'arbre construit, en général, les espèces de blé ont été divisées en tétraploïde et hexaploïde. Les espèces hexaploïdes étaient clairement divisées en deux groupes: à poil moyen - T. macha, T. aestivum, T. yunnanense et à poil long - T. vavilovii, T. petropavlovskyi, T. spelta. La seule exception est que la seule espèce sauvage polyploïde (tétraploïde) T. dicoccoides a été classée comme hexaploïde.
Dans le même temps, les espèces tétraploïdes comprenaient du blé hexaploïde à épi compact - T. compactum, T. antiquorum et T. sphaerococcum, et la lignée isogénique artificielle ANK-23 de blé tendre.
Essayer CNN

Pour résoudre le problème de la détermination de la ploïdie du blé à partir de l'image d'une épi, nous avons formé un réseau de neurones convolutifs de l'architecture EfficientNet B0 avec des poids pré-formés sur ImageNet. CrossEntropyLoss a été utilisé comme fonction de perte; Optimiseur Adam; la taille d'un lot est de 16; les images ont été redimensionnées à 224x224; le taux d'apprentissage a été modifié selon la stratégie fit_one_cycle avec un lr initial = 1e-4. Nous avons formé le réseau pendant 10 époques, en appliquant les augmentations suivantes au hasard: rotations de -20 + 20 degrés, changement de luminosité, contraste, saturation, mise en miroir. Le meilleur modèle a été choisi en fonction de la métrique AUC , dont la valeur a été calculée à la fin de chaque époque.
En conséquence, la précision sur l'échantillon différé AUC = 0,995 , ce qui correspond à la précision_score= 0,987 et une erreur de 1,3%. Ce qui est un très bon résultat.
Conclusion
Ce travail est un bon exemple de la façon dont une équipe de 5 étudiants et 2 conservateurs peut résoudre un problème biologique urgent et obtenir de nouveaux résultats scientifiques en quelques semaines.
Je tiens à exprimer ma gratitude à tous les participants à notre projet: Nikita Prokhoshin , Alexei Prikhodko , Evgeny Zavarzin , Artem Pronozin , Anna Paulish , Evgeny Komyshev, Mikhail Genaev .
Koval Vasily Sergeevich et Kruchinina Yulia Vladimirovna pour avoir tiré des épis de maïs.
Nikolai Petrovich Gontcharov et Afonnikov Dmitry Arkadyevich pour le matériel biologique fourni et leur aide dans l'interprétation des résultats.
Au Centre Mathématique de l'Université d'État de Novossibirsk et à l' Institut de Cytologie et de Génétique du SB RAS pour l'organisation de l'événement et la puissance de calcul.

PS Nous prévoyons de préparer la deuxième partie de l'article, où nous parlerons de la segmentation d'une oreille et de la sélection des épillets individuels.