Après avoir pris connaissance de KMath , j'ai décidé de généraliser cette optimisation à une variété de structures mathématiques et d'opérateurs définis dessus.
KMath est une bibliothèque de mathématiques et d'algèbre informatique qui utilise largement la programmation contextuelle dans Kotlin. KMath sépare les entités mathématiques (nombres, vecteurs, matrices) et les opérations sur celles-ci - elles sont fournies sous forme d'objet séparé, une algèbre correspondant au type d'opérandes, Algèbre <T> .
import scientifik.kmath.operations.*
ComplexField {
(i pow 2) + Complex(1.0, 3.0)
}Ainsi, après avoir écrit un générateur de bytecode, en tenant compte des optimisations JVM, vous pouvez obtenir des calculs rapides pour n'importe quel objet mathématique - il suffit de définir des opérations sur eux dans Kotlin.
API
Pour commencer, il était nécessaire de développer une API d'expressions et de passer ensuite à la grammaire du langage et à l'arbre de syntaxe. Il a également eu l'idée intelligente de définir l'algèbre sur les expressions elles-mêmes pour présenter une interface plus intuitive.
La base de l'ensemble de l'API d'expression est l'interface Expression <T> , et le moyen le plus simple de l'implémenter est de définir directement la méthode d' appel à partir des paramètres donnés ou, par exemple, des expressions imbriquées. Une implémentation similaire a été intégrée au module racine comme référence, bien que la plus lente.
interface Expression<T> {
operator fun invoke(arguments: Map<String, T>): T
}Des implémentations plus avancées sont déjà basées sur MST. Ceux-ci inclus:
- Interprète MST,
- Générateur de classe MST.
Une API pour analyser les expressions d'une chaîne vers MST est déjà disponible sur la branche de développement de KMath, tout comme le générateur de code JVM plus ou moins final.
Passons à MST. MST dispose actuellement de quatre types de nœuds:
- Terminal:
- symboles (c'est-à-dire variables)
- Nombres;
- opérations unaires;
- opérations binaires.
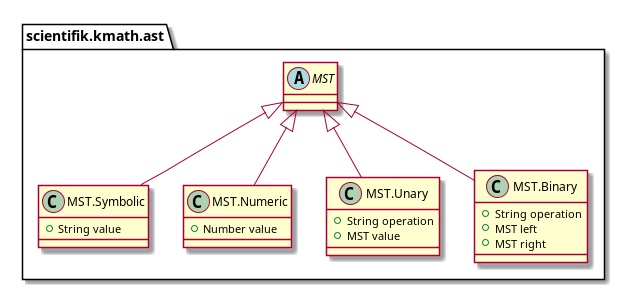
La première chose que vous pouvez faire est de contourner et de calculer le résultat à partir des données disponibles. En passant dans l'algèbre cible l'ID de l'opération, par exemple "+", et les arguments, par exemple 1.0 et 1.0 , on peut espérer le résultat si cette opération est définie. Sinon, une fois évaluée, l'expression échouera avec une exception.

Pour travailler avec MST, en plus du langage d'expression, il y a aussi l'algèbre - par exemple, MstField:
import scientifik.kmath.ast.*
import scientifik.kmath.operations.*
import scientifik.kmath.expressions.*
RealField.mstInField { number(1.0) + number(1.0) }() // 2.0Le résultat de la méthode ci-dessus est une implémentation de Expression <T> qui, lorsqu'elle est appelée, provoque une traversée de l'arborescence obtenue en évaluant la fonction passée à mstInField .
Génération de code
Mais ce n'est pas tout: lors de la traversée, on peut utiliser les paramètres de l'arborescence comme on veut et ne pas se soucier de l'ordre des actions et de l'arité des opérations. C'est ce qui est utilisé pour générer le bytecode.
La génération de code dans kmath-ast est un assemblage paramétré de la classe JVM. L'entrée est MST et l'algèbre cible, la sortie est l' instance Expression <T> .
La classe correspondante, AsmBuilder , et quelques autres extensions fournissent des méthodes pour créer impérativement du bytecode au-dessus d'ObjectWeb ASM. Ils donnent un aspect propre à la traversée MST et à l'assembly de classe et prennent moins de 40 lignes de code.
Considérez la classe générée pour l'expression "2 * x" , le code source Java décompilé à partir du bytecode est affiché:
package scientifik.kmath.asm.generated;
import java.util.Map;
import scientifik.kmath.asm.internal.MapIntrinsics;
import scientifik.kmath.expressions.Expression;
import scientifik.kmath.operations.RealField;
public final class AsmCompiledExpression_1073786867_0 implements Expression<Double> {
private final RealField algebra;
public final Double invoke(Map<String, ? extends Double> arguments) {
return (Double)this.algebra.add(((Double)MapIntrinsics.getOrFail(arguments, "x")).doubleValue(), 2.0D);
}
public AsmCompiledExpression_1073786867_0(RealField algebra) {
this.algebra = algebra;
}
}Tout d'abord, la méthode invoke a été générée ici , dans laquelle les opérandes ont été organisés séquentiellement (puisqu'ils sont plus profonds dans l'arborescence), puis l'appel add . Après l' appel , la méthode de pont correspondante a été enregistrée. Ensuite, le champ d' algèbre et le constructeur ont été écrits . Dans certains cas, lorsque les constantes ne peuvent pas être simplement placées dans le pool de constantes de classe , le champ constantes , le tableau java.lang.Object , est également écrit .
Cependant, en raison des nombreux cas extrêmes et optimisations, la mise en œuvre du générateur est plutôt compliquée.
Optimiser les appels à l'algèbre
Pour appeler une opération à partir de l'algèbre, vous devez transmettre son ID et ses arguments:
RealField { binaryOperation("+", 1.0, 1.0) } // 2.0Cependant, un tel appel est coûteux en termes de performances: pour choisir la méthode à appeler, RealField exécutera une instruction de tablewitch relativement coûteuse , et vous devez également vous souvenir de la boxe. Par conséquent, bien que toutes les opérations MST puissent être représentées sous cette forme, il est préférable de faire un appel direct:
RealField { add(1.0, 1.0) } // 2.0Il n'y a pas de convention spéciale sur le mappage des ID d'opération aux méthodes dans les implémentations d' Algebra <T> , nous avons donc dû insérer une béquille, dans laquelle il est écrit manuellement que "+" , par exemple, correspond à la méthode add. Il existe également un support pour les situations favorables où vous pouvez trouver une méthode pour un ID d'opération avec le même nom, le nombre d'arguments requis et leurs types.
private val methodNameAdapters: Map<Pair<String, Int>, String> by lazy {
hashMapOf(
"+" to 2 to "add",
"*" to 2 to "multiply",
"/" to 2 to "divide",
...private fun <T> AsmBuilder<T>.findSpecific(context: Algebra<T>, name: String, parameterTypes: Array<MstType>): Method? =
context.javaClass.methods.find { method ->
...
nameValid && arityValid && notBridgeInPrimitive && paramsValid
}Un autre problème majeur est la boxe. Si nous regardons les signatures de méthode Java obtenues après la compilation du même RealField, nous verrons deux méthodes:
public Double add(double a, double b)
// $FF: synthetic method
// $FF: bridge method
public Object add(Object var1, Object var2)Bien sûr, il est plus facile de ne pas s'embêter avec la boxe et le déballage et d'appeler la méthode bridge: elle est apparue ici à cause de l'effacement de type, afin d'implémenter correctement la méthode add (T, T): T , dont le type T dans le descripteur a été effacé en java.lang .Objet .
Appeler add directement à partir de deux doubles n'est pas non plus idéal, car la valeur de retour est la bauxite (il y a une discussion à ce sujet dans YouTrack Kotlin ( KT-29460 ), mais il est préférable de l'appeler afin de sauvegarder au mieux deux moulages d'objets d'entrée dans java.lang .Nombre et leur déballage à doubler .
Il a fallu le plus de temps pour résoudre ce problème. La difficulté ici n'est pas de créer des appels à une méthode primitive, mais du fait qu'il faut combiner les deux types primitifs (comme double) et leurs wrappers ( java.lang.Double , par exemple) sur la pile , et insérer la boxe aux bons endroits (par exemple, java.lang.Double.valueOf ) et unboxing ( doubleValue ) - il n'était absolument pas nécessaire de travailler avec des types d'instructions en bytecode.
J'avais des idées pour accrocher mon abstraction dactylographiée au-dessus du bytecode. Pour ce faire, j'ai dû approfondir l'API ObjectWeb ASM. J'ai fini par me tourner vers le backend Kotlin / JVM, examiné la classe StackValue en détail(un fragment typé de bytecode, qui conduit finalement à la réception d'une certaine valeur sur la pile d'opérandes), a compris l'utilitaire Type , qui vous permet d'utiliser facilement les types disponibles dans le bytecode (primitives, objets, tableaux), et réécrit le générateur avec son utilisation. Le problème de l'encadrement ou du déballage de la valeur sur la pile a été résolu par lui-même en ajoutant un ArrayDeque contenant les types attendus par l'appel suivant.
internal fun loadNumeric(value: Number) {
if (expectationStack.peek() == NUMBER_TYPE) {
loadNumberConstant(value, true)
expectationStack.pop()
typeStack.push(NUMBER_TYPE)
} else ...?.number(value)?.let { loadTConstant(it) }
?: error(...)
}conclusions
En fin de compte, j'ai pu créer un générateur de code en utilisant ObjectWeb ASM pour évaluer les expressions MST dans KMath. Le gain de performances sur une simple traversée MST dépend du nombre de nœuds, car le bytecode est linéaire et ne perd pas de temps sur la sélection des nœuds et la récursivité. Par exemple, pour une expression à 10 nœuds, la différence de temps entre l'évaluation avec la classe générée et l'interpréteur est de 19 à 30%.
Après avoir examiné les problèmes que j'ai rencontrés, j'ai tiré les conclusions suivantes:
- vous devez étudier immédiatement les capacités et les utilitaires d'ASM - ils simplifient considérablement le développement et rendent le code lisible ( Type , InstructionAdapter , GeneratorAdapter );
- MaxStack , , — ClassWriter COMPUTE_MAXS COMPUTE_FRAMES;
- ;
- , , , ;
- , — , , ByteBuddy cglib.
Merci d'avoir lu.
Auteurs de l'article:
Yaroslav Sergeevich Postovalov , MBOU “Lyceum № 130 nommé d'après Académicien Lavrentiev », membre du laboratoire de modélisation mathématique sous la direction de Voytishek Anton Vatslavovich
Tatyana Abramova , chercheur du laboratoire de méthodes d'expériences de physique nucléaire chez JetBrains Research .