Livre «Programmation des ordinateurs quantiques. Algorithmes de base et exemples de code "

Bonjour les Habitants! Les ordinateurs quantiques ont déclenché une nouvelle révolution informatique, et vous avez une grande chance de rejoindre la percée technologique dès maintenant. Les développeurs, les spécialistes de l'infographie et les aspirants professionnels de l'informatique trouveront dans ce livre des informations pratiques sur l'informatique quantique dont les programmeurs ont besoin. Au lieu d'étudier la théorie et les formules, vous vous concentrerez immédiatement sur des problèmes spécifiques qui démontrent les capacités uniques de la technologie quantique.



Eric Johnston, Nick Harrigan et Mercedes Gimeno-Segovia aident à développer les compétences et l'intuition nécessaires, ainsi qu'à maîtriser les outils nécessaires pour créer des applications quantiques. Vous comprendrez de quoi sont capables les ordinateurs quantiques et comment les appliquer dans la vraie vie. Le livre se compose de trois parties: - Programmation QPU: concepts de base de la programmation de processeurs quantiques, exécution d'opérations avec des qubits et téléportation quantique. - Primitives QPU: primitives et méthodes algorithmiques, amplification d'amplitude, transformée quantique de Fourier et estimation de phase. - Pratiquer QPU: résoudre des problèmes spécifiques en utilisant les primitives QPU, les méthodes de recherche quantique et l'algorithme de décomposition de Shor.

Données réelles

Les applications QPU complètes sont conçues pour fonctionner avec des données réelles, sans formation. Les données réelles ne sont pas toujours limitées aux entiers de base que nous avons parcourus jusqu'à présent. Par conséquent, la question de savoir comment représenter des données plus complexes dans QPU en vaut la peine, et de bonnes structures de données peuvent être tout aussi importantes que de bons algorithmes. Dans ce chapitre, nous allons essayer de répondre à deux questions qui ont été précédemment contournées:

1. Comment représenter des types de données complexes dans le registre QPU? Un entier positif peut être représenté dans un codage binaire simple. Mais qu'en est-il des nombres irrationnels, ou même des types de données composites comme les vecteurs ou les matrices? Cette question prend une nouvelle profondeur lorsque l'on considère que la superposition et la phase relative peuvent fournir de nouvelles options de codage quantique pour ces types de données.
2. , QPU? , WRITE . , QPU . , , , QPU , .

Commençons par la première question. Lors de la description des représentations QPU pour des types de données de complexité croissante, nous arriverons à l'introduction de structures de données quantiques à part entière et au concept de mémoire à accès aléatoire quantique (QRAM). La RAM quantique est une ressource essentielle pour de nombreuses applications QPU pratiques.



Le contenu des chapitres suivants dépendra fortement des structures de données présentées dans ce chapitre. Par exemple, le codage d'amplitude complexe qui sera décrit pour les données vectorielles est au cœur de toutes les applications d'apprentissage automatique quantique présentées au chapitre 13.

Données non cibles

Comment encoder des données numériques non entières dans le registre QPU? Les deux méthodes standard pour représenter ces valeurs en binaire sont les représentations à virgule fixe et à virgule flottante. Bien que la représentation en virgule flottante soit plus flexible (et adaptable à la plage de valeurs qui doivent être représentées avec un certain nombre de bits), en raison de la valeur élevée des qubits et de notre désir de simplicité, la représentation en virgule fixe est un meilleur endroit pour commencer.



Les nombres à virgule fixe sont souvent décrits en notation Q (malheureusement, Q dans ce cas ne signifie pas "quantique"). Cela permet de supprimer l'ambiguïté quant à la fin des bits fractionnaires et à l'endroit où les bits entiers commencent. La notation Qn.m désigne un registre à n bits, dont les m bits sont pour la partie fractionnaire (et par conséquent, les autres (n - m) contiennent la partie entière). Bien sûr, vous pouvez utiliser la même notation pour spécifier comment le registre QPU doit être utilisé pour coder un nombre à virgule fixe. Par exemple, sur la Fig. 9.1 représente un registre QPU à huit qubits, qui code la valeur 3,640625 dans la représentation en virgule fixe Q8.6.



Dans l'exemple donné, le nombre sélectionné peut être codé avec précision en représentation en virgule fixe, car 3.640625 =Bien sûr, une telle chance n'est pas toujours trouvée. L'augmentation du nombre de bits dans la partie entière d'un registre à virgule fixe élargit la plage de valeurs entières qui peuvent être représentées, tandis que l'augmentation du nombre de bits dans la partie fractionnaire améliore la précision de la partie fractionnaire d'un nombre. Plus il y a de qubits dans la partie fractionnaire, plus il est probable qu'une combinaison 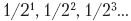puisse représenter avec précision un nombre donné.





Bien que nous mentionnerons brièvement l'utilisation de la représentation en virgule fixe dans les chapitres suivants, elle joue un rôle extrêmement important dans l'expérimentation de données réelles dans de petits registres QPU. Lorsque vous travaillez avec différentes méthodes de codage, vous devez surveiller attentivement le codage spécifique utilisé pour les données d'un registre QPU particulier afin d'interpréter correctement l'état de ses qubits.

QRAM

Les registres QPU peuvent stocker des représentations de différentes valeurs numériques, mais comment y stocker ces valeurs? Les données initialisées manuellement deviennent très rapidement obsolètes. Ce dont nous avons vraiment besoin, c'est de pouvoir lire les valeurs de la mémoire, en récupérant les valeurs stockées à une adresse binaire. Le programmeur travaille avec la mémoire vive traditionnelle en utilisant deux registres: l'un est initialisé avec une adresse mémoire et l'autre reste non initialisé. La mémoire à accès aléatoire écrit dans le second registre les données binaires stockées à l'adresse spécifiée par le premier registre, comme le montre la Fig. 9.2.





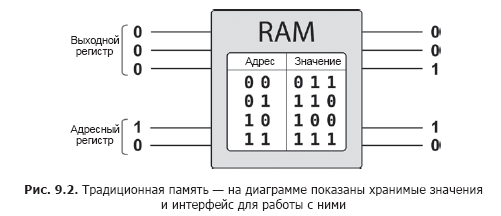
La mémoire traditionnelle peut-elle être utilisée pour stocker les valeurs destinées à initialiser les registres QPU? Bien sûr, l'idée semble séduisante.



Si vous souhaitez initialiser le registre QPU avec une seule valeur traditionnelle (complément à deux, codage binaire à virgule fixe ou simple), alors la RAM est très bien. La valeur souhaitée est simplement stockée en mémoire, et write () et read () sont utilisés pour écrire ou lire à partir du registre QPU. C'est ce mécanisme limité qui a été utilisé par le code JavaScript de QCEngine pour interagir avec les registres QPU jusqu'à présent.



Par exemple, l'exemple de code du Listing 9.1, qui reçoit un tableau a et implémente l'opération a [2] + = 1 ;, récupère implicitement ce tableau de valeurs dans la RAM pour initialiser le registre QPU. Le circuit est illustré à la Fig. 9.3.

Exemple de code

Cet exemple peut être réalisé en ligne à l' adresse http://oreilly-qc.github.io?p=9-1.

Liste 9.1. Utilisation de QPU pour augmenter le nombre en mémoire

var a = [4, 3, 5, 1];

qc.reset(3);
var qreg = qint.new(3, 'qreg');

qc.print(a);
increment(2, qreg);
qc.print(a);

function increment(index, qreg)
{
      qreg.write(a[index]);
      qreg.add(1);
      a[index] = qreg.read();
}

Il est à noter que dans ce cas simple, non seulement la RAM traditionnelle est utilisée pour stocker l'entier, mais également le processeur traditionnel indexe le tableau pour sélectionner et transmettre le QPU de la valeur souhaitée.



Bien que cette utilisation de la RAM permette d'initialiser les registres QPU à de simples valeurs binaires, elle présente de sérieuses limitations. Que faire si vous devez initialiser le registre QPU avec la superposition des valeurs stockées? Par exemple, supposons que dans la RAM, la valeur 3 (110) est stockée à l'adresse 0x01 et la valeur 5 (111) est stockée à l'adresse 0x11. Comment préparer le registre d'entrée dans une superposition de ces deux valeurs?



Avec la RAM traditionnelle et l'opération traditionnelle maladroite write (), cela ne fonctionnera pas. Les processeurs quantiques, tout comme leurs ancêtres tubes, auront besoin d'un équipement de mémoire fondamentalement nouveau - de nature quantique. Meet Quantum Random Access Memory (QRAM) vous permet de lire et d'écrire des données au niveau quantique. Il y a déjà quelques idées sur la façon de construire physiquement QRAM, mais il convient de noter que l'histoire peut bien se répéter et que des processeurs quantiques incroyablement puissants peuvent apparaître bien avant qu'il n'y ait de matériel de mémoire quantique exploitable.



Cela vaut la peine d'expliquer un peu plus précisément ce que fait QRAM. Comme la mémoire traditionnelle, QRAM reçoit deux registres en entrée: le registre d'adresse QPU pour l'adresse mémoire et le registre de sortie QPU, qui renvoie la valeur stockée à l'adresse donnée. Pour QRAM, les deux registres sont composés de qubits. Cela signifie que dans le registre d'adresse, il est possible de définir une superposition de cellules de mémoire et, par conséquent, d'obtenir une superposition des valeurs correspondantes dans le registre de sortie (Fig. 9.4).





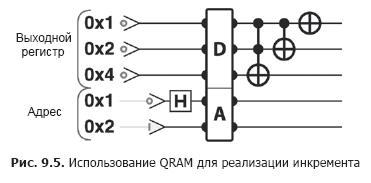
Ainsi QRAM vous permet en fait de lire les valeurs stockées en superposition. Les amplitudes complexes exactes de la superposition à obtenir dans le registre de sortie sont déterminées par la superposition prévue dans le registre d'adresse. En figue. La Figure 9.2 montre les différences lors de l'exécution de la même opération d'incrémentation dans le Listing 9.1 (Figure 9.5), mais en utilisant QRAM pour accéder aux données au lieu d'opérations de lecture / écriture QPU. La lettre "A" désigne le registre dans lequel l'adresse QRAM (ou superposition) est transmise. La lettre "D" désigne le registre dans lequel QRAM renvoie la superposition correspondante de valeurs stockées (données).

Exemple de code

Cet exemple peut être fait en ligne à oreilly-qc.github.io?p=9-2 .

Liste 9.2. Utilisation de QPU pour incrémenter un nombre de QRAM - le registre d'adresse peut contenir une superposition, ce qui entraînera le registre de sortie pour contenir une superposition de valeurs stockées

var a = [4, 3, 5, 1];
var reg_qubits = 3;
qc.reset(2 + reg_qubits + qram_qubits());
var qreg = qint.new(3, 'qreg');
var addr = qint.new(2, 'addr');
var qram = qram_initialize(a, reg_qubits);

qreg.write(0);
addr.write(2);
addr.hadamard(0x1);

qram_load(addr, qreg);
qreg.add(1);

Cette description de QRAM peut sembler trop vague - qu'est-ce que le matériel de mémoire quantique? Dans ce livre, nous ne donnerons pas une description de la façon de construire QRAM dans la pratique (comme, par exemple, la plupart des livres sur C ++ ne fournissent pas une description détaillée du fonctionnement de la mémoire traditionnelle). Les exemples de code comme celui du Listing 9.2 sont exécutés à l'aide d'un modèle simplifié qui imite le comportement de QRAM. Néanmoins, des prototypes de technologies QRAM existent.



Alors que la mémoire quantique sera un composant essentiel de tout QPU sérieux, les détails de mise en œuvre sont susceptibles de changer, comme avec tout appareil informatique quantique. Ce qui est important pour nous, c'est l'idée même d'une ressource fondamentale qui se comporte comme le montre la Fig. 9.4, et les applications puissantes qui peuvent être construites dessus.

Avec la mémoire quantique à votre disposition, vous pouvez passer à la création de structures de données quantiques complexes. Les structures qui vous permettent de représenter des données vectorielles et matricielles sont particulièrement intéressantes.

Encodage vectoriel

Supposons que vous souhaitiez initialiser le registre QPU pour représenter un vecteur simple comme l'équation 9.1.



Formule 9.1. Un exemple de vecteur d'initialisation du registre QPU.





Les données sous cette forme se trouvent souvent dans les applications d'apprentissage automatique quantique.

La méthode la plus évidente pour coder des données vectorielles est peut-être de représenter chaque composant comme un registre QPU séparé avec une représentation binaire appropriée. Nous appellerons cette méthode (probablement la plus évidente) l'encodage d'état de méthode pour les vecteurs. Le vecteur de l'exemple donné peut être codé dans quatre registres à deux qubits, comme le montre la Fig. 9.6.





L'un des problèmes du codage d'état naïf est qu'il gaspille des qubits - la ressource la plus précieuse d'un QPU. Cependant, l'un des avantages des vecteurs traditionnels à code d'état est qu'ils ne nécessitent pas de mémoire quantique. Les composantes vectorielles peuvent simplement être stockées dans la mémoire standard et utiliser leurs valeurs séparées pour contrôler la préparation de chaque registre QPU individuel. Mais cet avantage sous-tend également l'inconvénient le plus sérieux du codage d'état vectoriel: stocker les données vectorielles de cette manière traditionnelle nous empêche d'utiliser les capacités non traditionnelles de QPU. Pour utiliser la puissance du QPU, il faut être capable de manipuler les phases relatives des superpositions, et ce n'est pas facile à faire,si chaque composant d'un vecteur traite réellement votre processeur quantique comme une collection de registres binaires traditionnels!



Au lieu de cela, vous devez descendre au niveau quantique. Supposons que les composantes vectorielles soient stockées dans la superposition des amplitudes d'un registre QPU. Puisqu'un registre QPU de n qubits peut exister dans une superposition avec 2n amplitudes (et par conséquent, il y aura 2n cercles pour les expériences avec enregistrement circulaire), il est possible de représenter le codage d'un vecteur avec n composantes dans un registre QPU avec ceil (log (n)) qubits.



Pour l'exemple de vecteur de la formule 9.1, cette approche nécessiterait un registre à deux qubits - l'idée est de trouver un schéma quantique approprié pour coder les données vectorielles de la figure 1. 9.7.





Appelons ces données vectorielles quantiques uniques codant un codage d'amplitude complexe. Il est important d'apprécier les différences entre un codage d'amplitude complexe et un codage d'état plus conventionnel. Table 9.1 compare les deux méthodes de codage pour différentes données vectorielles. Le dernier exemple de codage d'état nécessitera quatre registres de 7 bits, dont chacun utilise une représentation à virgule fixe de Q7.7.



Tableau 9.1. Différences entre les méthodes de codage des données vectorielles (codage d'amplitude complexe et codage d'état)





Pour obtenir des vecteurs avec un codage d'amplitude complexe dans QCEngine, vous pouvez utiliser la fonction pratique amplitude_encode (). Le programme du Listing 9.3 prend un vecteur de valeurs et une référence à un registre QPU (qui doit être suffisamment grand) et prépare ce registre en effectuant un codage d'amplitude complexe sur le vecteur.

Exemple de code

Cet exemple peut être fait en ligne à oreilly-qc.github.io?p=9-3 .



Liste 9.3. Préparation de vecteurs avec codage d'amplitude complexe dans QCEngine

//     ,    
//   2
var vector = [-1.0, 1.0, 1.0, 5.0, 5.0, 6.0, 6.0, 6.0];

//        
//  
var num_qubits = Math.log2(vector.length);
qc.reset(num_qubits);
var amp_enc_reg = qint.new(num_qubits, 'amp_enc_reg');

//      amp_enc_reg
amplitude_encode(vector, amp_enc_reg);

Dans cet exemple, le vecteur est simplement passé en tant que tableau JavaScript stocké dans la mémoire traditionnelle - même si nous avons indiqué que le codage d'amplitude complexe dépend de la QRAM. Comment QCEngine effectue-t-il un codage d'amplitude complexe lorsque seule la RAM de votre ordinateur est disponible pour le programme? Bien qu'il soit possible de générer un schéma de codage d'amplitude complexe sans QRAM, cela ne peut certainement pas être fait efficacement. QCEngine fournit un modèle lent mais réalisable de ce qui peut être réalisé avec l'accès QRAM.

Limitations du codage d'amplitude complexe

L'idée derrière le codage d'amplitude complexe semble excellente au début - il utilise moins de qubits et fournit des outils quantiques pour travailler avec des données vectorielles. Dans toute application utilisant ce mécanisme, deux facteurs importants doivent être pris en compte.

Problème 1: résultats quantiques

Vous avez peut-être déjà remarqué la première de ces restrictions: les superpositions quantiques ne peuvent généralement pas être lues par READ. Notre principal ennemi encore! Si vous répartissez les composantes vectorielles sur la superposition quantique, elles ne peuvent pas être lues à nouveau. Naturellement, cela ne crée pas de problèmes particuliers lors du transfert de données vectorielles vers l'entrée d'un autre programme QPU depuis la mémoire. Mais très souvent, les applications QPU qui reçoivent des données vectorielles complexes codées AM à l'entrée génèrent également des données vectorielles complexes codées AM en sortie.



Ainsi, l'utilisation d'un codage d'amplitude complexe restreint considérablement notre capacité à lire la sortie de l'application avec une opération READ. Heureusement, il est souvent possible d'extraire des informations utiles à partir de résultats de codage d'amplitude complexes. Comme vous le verrez dans les chapitres suivants, bien que vous ne puissiez pas reconnaître les composants individuels, vous pouvez découvrir les propriétés globales des vecteurs encodés de cette manière. Cependant, le codage d'amplitude complexe n'est pas une panacée, et son application réussie nécessite attention et ingéniosité.

Problème 2: la nécessité de normaliser les vecteurs

Le deuxième problème associé au codage d'amplitude complexe est caché dans le tableau. 9.1. Regardez de plus près le codage d'amplitude complexe des deux premiers vecteurs du tableau: [0,1,2,3] et [6,1,1,4]. Les amplitudes complexes d'un registre QPU à deux qubits peuvent-elles prendre les valeurs [0,1,2,3] ou les valeurs [6,1,1,4]? Malheureusement non. Dans les chapitres précédents, nous avons généralement contourné la discussion des amplitudes et des phases relatives au profit d'une notation circulaire plus intuitive. Si cette approche était plus intuitive, elle vous protégeait d'une règle numérique importante concernant les amplitudes complexes: les carrés des amplitudes complexes d'un registre doivent s'additionner à 1. Cette exigence, appelée normalisation, a du sens quand on se souvient que les carrés des amplitudes dans le registre correspondent aux probabilités de lecture. résultats différents.Puisqu'il faut obtenir un résultat, ces probabilités (et, par conséquent, les carrés de toutes les amplitudes complexes) devraient s'additionner à 1. Lors de l'utilisation d'une notation circulaire pratique, il est facile d'oublier la normalisation, mais elle impose une contrainte importante sur quel vecteur un codage d'amplitude complexe peut être appliqué aux données. Les lois de la physique ne permettent pas de créer un registre en superposition d'amplitudes complexes [0,1,2,3] ou [6,1,1,4].étant en superposition avec des amplitudes complexes [0,1,2,3] ou [6,1,1,4].qui est en superposition avec des amplitudes complexes [0,1,2,3] ou [6,1,1,4].



Pour appliquer un codage d'amplitude complexe à deux vecteurs de problème du tableau. 9.1, vous devez d'abord les normaliser en divisant chaque composant par la somme des carrés de tous les composants. Par exemple, dans le codage d'amplitude complexe du vecteur [0,1,2,3], vous devez d'abord diviser toutes les composantes par 3,74 pour obtenir un vecteur normalisé [0,00, 0,27, 0,53, 0,80], qui convient désormais au codage en amplitudes de superposition complexes.



La normalisation des données vectorielles a-t-elle des effets indésirables? On dirait que les données ont complètement changé! En fait, la normalisation laisse la plupart des informations importantes inchangées (dans la représentation géométrique, elle met simplement à l'échelle la longueur du vecteur, laissant la direction inchangée). Pouvons-nous supposer que les données normalisées remplacent complètement les données d'origine? Cela dépend des besoins de l'application QPU particulière dans laquelle vous avez l'intention de les utiliser. N'oubliez pas que vous pouvez stocker la valeur numérique du facteur de normalisation dans un registre différent si nécessaire.

Codage d'amplitude complexe et enregistrement circulaire

Lorsque vous commencez à réfléchir plus spécifiquement aux valeurs numériques des amplitudes complexes des registres, il peut être utile de vous rappeler comment les amplitudes complexes sont représentées en notation circulaire et de remarquer un éventuel écueil. Les zones remplies en notation circulaire représentent les carrés des amplitudes des amplitudes complexes de l'état quantique. Dans des situations telles que le codage d'amplitude complexe, où les amplitudes complexes doivent représenter les composantes d'un vecteur avec des valeurs réelles, cela signifie que les zones remplies sont déterminées par le carré de la composante vectorielle correspondante, et non par la composante elle-même. En figue. 9.8 montre comment interpréter correctement la représentation du vecteur [0,1,2,3] après normalisation en notation circulaire.





Vous en savez maintenant assez sur les vecteurs codés en amplitude complexes pour comprendre les applications QPU qui seront présentées dans le livre. Mais pour de nombreuses applications, en particulier celles liées à l'apprentissage automatique quantique, il est nécessaire d'aller plus loin et d'utiliser QPU pour manipuler non seulement des vecteurs, mais également des matrices de données entières. Comment encodez-vous des tableaux de nombres à deux dimensions?



»Plus de détails sur le livre peuvent être trouvés sur le site de l'éditeur

» Table des matières

» Extrait



Pour Habitants un rabais de 25% sur le coupon - Programmation



Lors du paiement de la version papier du livre, un e-book est envoyé à l'e-mail.