Les physiciens ont découvert la structure algébrique sous-jacente aux mathématiques complexes des collisions de particules. Certains espèrent que cela nous conduira à une théorie plus élégante du monde physique.
Lorsque les physiciens des particules tentent de modéliser des expériences, ils sont confrontés à des calculs impossibles en raison d'une équation infiniment grande qui est hors de portée des mathématiques modernes.
Heureusement, ils peuvent faire des prédictions généralement précises sans passer par toutes ces mathématiques cryptiques jusqu'à la fin. Pour raccourcir les calculs, les scientifiques du Grand collisionneur de hadrons du CERN, en Europe, font des prédictions qui coïncident avec les événements qu'ils observent ensuite lors de collisions de particules subatomiques balayant à une vitesse énorme le long d'une piste de 26 kilomètres.
Malheureusement, l'ère de l'accord entre la prédiction et l'observation touche peut-être à sa fin. Plus les mesures sont précises, plus il est difficile pour les schémas de calcul approximatifs utilisés par les théoriciens de suivre.
«Nous sommes déjà sur le point d'épuiser les fonds dont nous disposons», a déclaré Claude Dar , physicien des particules au CERN.
Cependant, trois travaux récents de Pierpaolo Mastrolia de l'Université de Padoue en Italie et de Sebastian Mizeradu Princeton Institute for Advanced Research dans le New Jersey, a découvert la structure mathématique sous-jacente à ces équations. Il fournit une nouvelle façon de réduire un nombre infini de membres en une douzaine de composants requis. Leur méthode peut aider à amener la précision de la prédiction au niveau suivant dont les théoriciens ont besoin pour aller au-delà du modèle principal mais incomplet de la physique des particules.
«Ils ont montré de nombreux résultats prouvant la viabilité de cette technique prometteuse», a déclaré Dar.
Cependant, les avantages peuvent être bien plus importants que la simple amélioration des prévisions. La nouvelle méthode contourne les mathématiques ennuyeuses traditionnelles en calculant directement des «nombres d'intersection», qui, selon certains, peuvent finalement nous donner une description plus élégante du monde subatomique.
«Ce ne sont pas que des mathématiques», a déclaré Simon Caron-Hewot de l'Université McGill, un théoricien quantique qui étudie les implications des travaux de Mastrolius et Mizera. "Tout cela est très étroitement lié à la théorie quantique des champs."
Boucle infinie
Lors de la modélisation des collisions de particules, les physiciens utilisent des diagrammes de Feynman , une notation simple inventée par Richard Feynman dans les années 1940.
Pour comprendre le fonctionnement de cet enregistrement, considérons un événement simple: deux quarks se rapprochent, échangent un gluon dans le processus de «collision», puis rebondissent sur des trajectoires différentes.
Dans le diagramme de Feynman, les chemins des quarks sont indiqués par des «jambes», qui forment des «sommets» à la jonction pendant l'interaction des particules. Feynman a développé des règles pour transformer une telle image en équations qui calculent la probabilité que cet événement se produise. Vous écrivez une fonction spécifique pour chaque jambe et sommet - généralement une fraction utilisant la masse et l'élan de la particule - et vous multipliez le tout. Pour des options simples comme la nôtre, les calculs peuvent tenir sur une serviette.
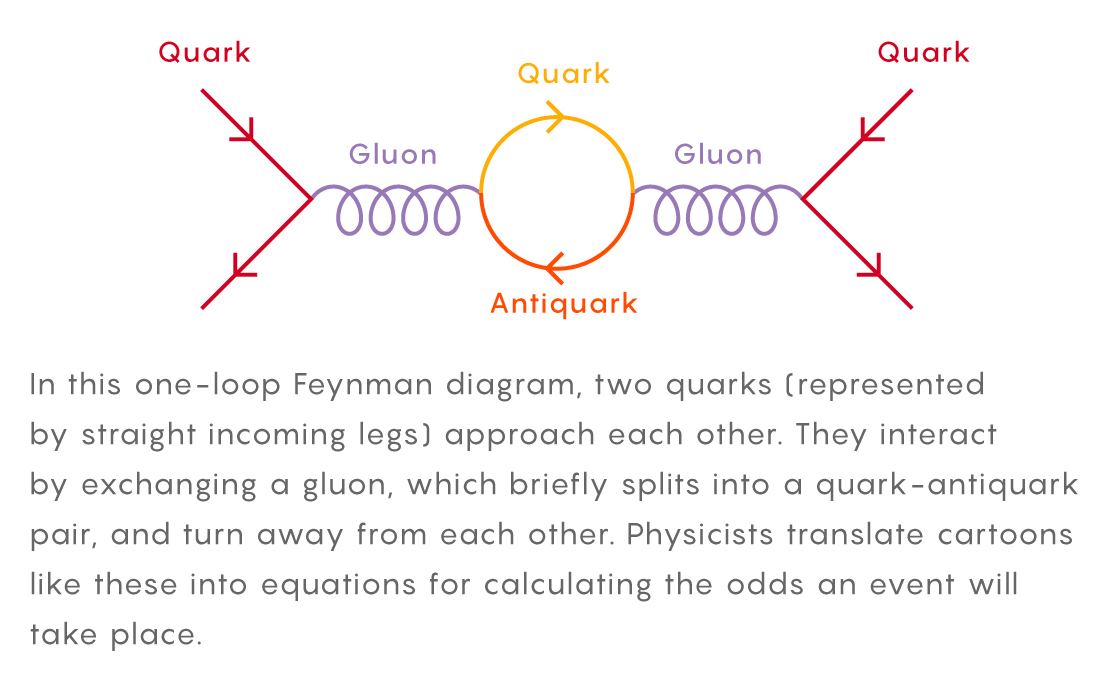
Dans ce diagramme, deux quarks (indiqués par des jambes droites avec des flèches pointant vers l'intérieur) s'approchent d'une boucle. Ils interagissent, échangeant des gluons, qui pendant une courte période de temps se sont séparés en une paire quark-antiquark, puis s'envolent. Les physiciens traduisent ces modèles en équations qui calculent la probabilité que cet événement se produise.
Cependant, la règle d'or de la théorie quantique est de considérer toutes les possibilités, et l'échange d'un simple gluon n'est que l'un des nombreux scénarios qui peuvent se dérouler lorsque deux quarks entrent en collision. Un gluon échangé entre des particules peut se diviser en une paire quark-antiquark pendant une courte période de temps, puis redevenir un gluon. Deux quarks se rencontrent et deux quarks divergent, mais il peut se passer beaucoup de choses entre les deux. Pour rendre pleinement compte de ce qui se passe et donner une prédiction idéale, vous devrez dessiner un nombre infini de diagrammes. Personne ne s'attend à des résultats parfaits, mais la clé pour améliorer la précision des calculs est d'aller aussi loin que possible le long de la chaîne sans fin des événements.
Et c'est là que les physiciens sont bloqués.
Pour étudier ce centre caché plus en détail, vous devez vous tourner vers les particules virtuelles - des fluctuations quantiques qui affectent progressivement le résultat de chaque interaction. L'existence à court terme du couple de quarks mentionné ci-dessus, comme de nombreux événements virtuels, est indiquée sur le diagramme de Feynman par une boucle fermée. Les boucles déconcertent les physiciens - ce sont des boîtes noires qui ajoutent des couches supplémentaires à des scénarios sans fin. Afin de calculer en quelque sorte les possibilités impliquées par la boucle, les théoriciens doivent prendre des intégrales. Ces intégrales atteignent des proportions monstrueuses dans les diagrammes de Feynman avec de nombreuses boucles qui apparaissent au fur et à mesure que les chercheurs avancent le long de la chaîne d'événements et rendent compte d'interactions virtuelles de plus en plus complexes.
Les physiciens disposent d'algorithmes pour calculer les probabilités de scénarios sans boucles ou avec une boucle, mais déjà des collisions avec deux boucles mettent les ordinateurs à genoux. C'est le plafond de la précision prédictive - et pour les physiciens de comprendre les implications de la théorie quantique.
Cependant, tout cela a un côté positif: les physiciens n'ont pas besoin de calculer absolument toutes les intégrales d'un diagramme de Feynman complexe, car la plupart d'entre elles peuvent être rassemblées en un seul.
Des milliers d'intégrales peuvent être réduites à plusieurs dizaines d'intégrales «de base», auxquelles on peut donner des poids et les ajouter. Mais quelles intégrales peuvent être rassemblées dans des intégrales de base séparées est une question de calcul difficile. Les chercheurs utilisent des ordinateurs qui font essentiellement des suppositions basées sur des millions d'interactions et ont du mal à obtenir des combinaisons significatives d'intégrales.
Cependant, grâce aux nombres d'intersection, les physiciens peuvent avoir trouvé un moyen de sélectionner élégamment des informations importantes à partir de calculs tentaculaires d'intégrales de Feynman.
Empreinte géométrique
Le travail de Mastrolia et Mizera découle d'une ramification des mathématiques telle que la topologie algébrique , qui classe les formes et les espaces. Aide dans ces théories de " cohomologie ", vous permettant de calculer des "empreintes digitales" algébriques à partir d'espaces géométriques complexes.
"C'est un peu comme un synopsis, un dispositif algébrique qui capture l'essence de l'espace que vous explorez", a déclaré Clément Dupont, mathématicien à l'Université de Montpellier en France.
Les diagrammes de Feynman peuvent être traduits en espaces géométriques, qui peuvent ensuite être analysés en utilisant la cohomologie. Chaque point de cet espace peut représenter l'un des nombreux scénarios qui se déroulent lorsque des particules entrent en collision.
Nous pourrions espérer qu'en prenant la cohomologie de cet espace - en trouvant sa structure algébrique - vous pourriez calculer les poids pour les intégrales fondamentales. Cependant, l'espace géométrique qui caractérise la plupart des diagrammes de Feynman est si courbé qu'il résiste à de nombreux calculs cohomologiques.
En 2017, Mizera tentait d'analyser les collisions d'objets dans la théorie des cordes lorsqu'il est tombé sur des outils inventés pour la première fois par Israel Gelfand et Katsuhiko Aomoto dans les années 1970 et 1980 alors qu'ils travaillaient sur une cohomologie appelée cohomologie tordue. Plus tard la même année, Mizera a rencontré Mastrolia, qui s'est rendu compte que ces techniques pouvaient également fonctionner sur le diagramme de Feynman. L'année dernière, ils ont publié trois articles qui utilisaient la théorie de la cohomologie pour accélérer les calculs de collisions de particules simples.
Leur méthode prend une famille de scénarios physiques interconnectés, le présente comme un espace géométrique et calcule sa cohomologie tordue. «Et cette cohomologie tordue dit tout sur les intégrales qui nous intéressent», a déclaré Mizera.
En particulier, la cohomologie tordue indique combien d'intégrales de base sont nécessaires et quels devraient être leurs poids. Ces poids apparaissent sous forme de valeurs qu'ils appellent «numéros d'intersection». En conséquence, des milliers d'intégrales sèchent jusqu'à une somme pondérée de plusieurs dizaines d'intégrales de base.
Il est possible que les théories de cohomologie qui produisent ces nombres d'intersection puissent faire plus que simplement faciliter le calcul - elles peuvent nous indiquer la signification physique des quantités les plus importantes dans le calcul.
Par exemple, lorsqu'un gluon virtuel se désintègre en deux quarks virtuels, leur durée de vie peut être différente. Dans l'espace géométrique qui leur est associé, chaque point peut désigner une durée de vie de quark différente. Lors du calcul des poids, les chercheurs constatent que les scénarios avec les particules virtuelles les plus durables - c'est-à-dire les cas où les particules deviennent presque réelles - ont le plus d'impact sur le résultat.
«C'est ce qui est incroyable avec cette méthode», a déclaré Karon-Hewot. "Il recrée tout à partir de ces rares événements spéciaux."
La semaine dernière, Mizera, Mastrolia et leurs collègues ont publié une autre pré-impression, où il est montré que cette technique a suffisamment évolué pour fonctionner avec de vrais diagrammes à deux boucles. Dans le prochain travail, Karon-Hewot développera encore plus cette méthode, en apprivoisant peut-être même les diagrammes à trois boucles.
En cas de succès, cette technique pourrait aider à ouvrir une nouvelle génération de prédictions théoriques. Et, comme certains chercheurs le soupçonnent, cela peut même nous montrer une nouvelle perspective sur la réalité.