Apprentissage automatique. Réseaux de neurones (partie 2): modélisation OU; XOR avec TensorFlow.js

L'article est la suite d'une série d'articles consacrés à l'apprentissage automatique à l'aide de la bibliothèque TensorFlow.JS, l'article précédent fournit la partie théorique générale de la formation du réseau de neurones le plus simple composé d'un neurone: l'



apprentissage automatique. Réseaux de neurones (partie 1): Le processus d'apprentissage du perceptron



Dans cet article, nous utiliserons un réseau de neurones pour modéliser l'exécution d'opérations OR logiques; XOR, qui est une sorte d'application "Hello World" pour les réseaux de neurones.

L'article décrira étape par étape le processus d'une telle modélisation à l'aide de TensorFlow.js.



Construisons donc un réseau de neurones pour l'opération OR logique. En entrée, nous enverrons toujours deux signaux X ₁ et X ₂ , et en sortie, nous recevrons un signal de sortie Y. Pour entraîner le réseau neuronal, nous avons également besoin d'un jeu de données d'entraînement (Figure 1).





Figure 1 - Un jeu de données d'apprentissage et un modèle pour modéliser une opération OU logique



Pour comprendre quelle structure d'un réseau de neurones définir, imaginons un jeu de données d'apprentissage sur un plan de coordonnées avec les axes X ₁ et X ₂ (Figure 2, à gauche).





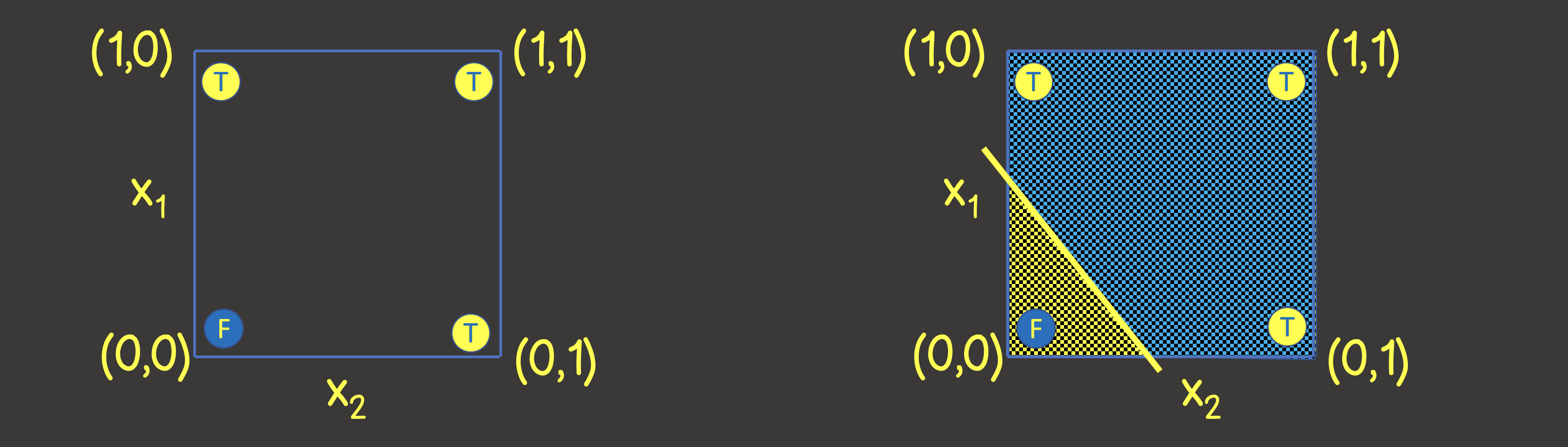
Figure 2 - Ensemble d'entraînement sur le plan de coordonnées pour une opération OR logique



Veuillez noter que pour résoudre ce problème, il nous suffit de tracer une ligne qui diviserait le plan de telle sorte que d'un côté de la ligne il y ait toutes les valeurs VRAIES , et de l'autre - toutes les valeurs FAUX (Figure 2, à droite). Nous savons également qu'un neurone dans un réseau de neurones (perceptron) peut parfaitement faire face à cet objectif, dont la valeur de sortie est calculée à partir des signaux d'entrée comme:

$$

$$y=x_1w_1+x_2w_2$$

qui est une représentation mathématique de l'équation d'une ligne droite.



Compte tenu du fait que nos valeurs sont comprises entre 0 et 1, nous appliquons également la fonction d'activation sigmoïde. Ainsi, notre réseau de neurones ressemble à celui de la figure 3.



Figure 3 - Un réseau de neurones pour l'entraînement du fonctionnement logique OU Résolvons



donc ce problème en utilisant TensorFlow.js.



Tout d'abord, nous devons convertir l'ensemble de données d'entraînement en tenseurs. Un tenseur est un conteneur de données qui peut avoir$$$N$axes et un nombre arbitraire d'éléments le long de chacun des axes. La plupart des tenseurs sont familiers avec les mathématiques - vecteurs (tenseur à un axe), matrices (tenseur à deux axes - lignes, colonnes).



Pour définir le jeu de données d'entraînement, le premier axe (axe 0) est toujours l'axe le long duquel toutes les instances d'échantillons de données disponibles sont situées (Figure 4).





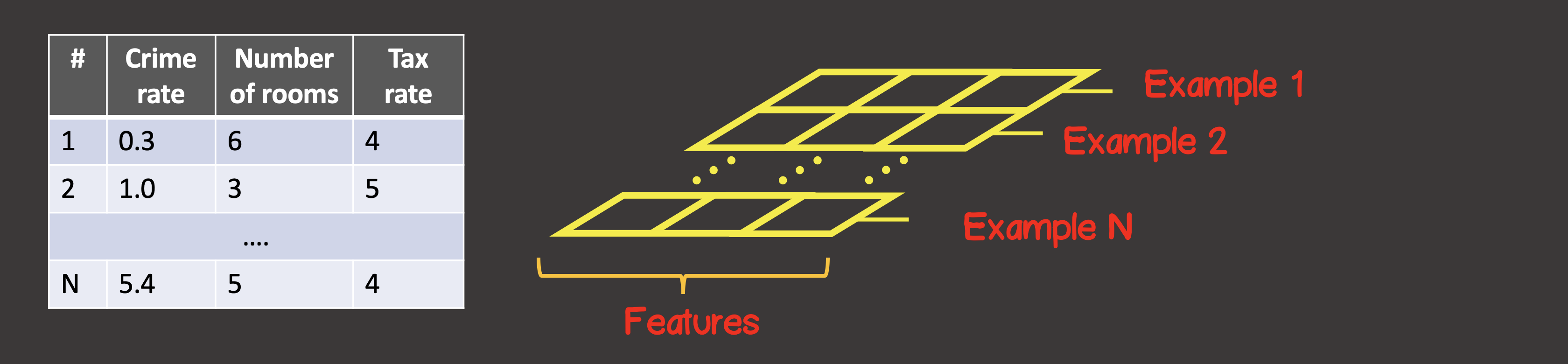
Figure 4 - Structure



du tenseur Dans notre cas particulier, nous avons 4 instances d'échantillons de données (Figure 1), ce qui signifie que le tenseur d'entrée le long du premier axe aura 4 éléments. Chaque élément de l'échantillon d'apprentissage est un vecteur composé de deux éléments X ₁ , X ₂ . Ainsi, le tenseur d'entrée a 2 axes (matrice), le long du premier axe il y a 4 éléments, le long du second axe - 2 éléments.

const input = [[0, 0], [1, 0], [0, 1], [1, 1]];
const inputTensor = tf.tensor(input, [input.length, 2]);

De même, convertissez la sortie en un tenseur. En ce qui concerne les signaux d'entrée, le long du premier axe, nous avons 4 éléments, et chaque élément contient un vecteur contenant une valeur:

const output = [[0], [1], [1], [1]]
const outputTensor = tf.tensor(output, [output.length, 1]);

Créons un modèle à l'aide de l'API TensorFlow:

const model = tf.sequential();
model.add(
      tf.layers.dense({ inputShape: [2], units: 1, activation: 'sigmoid' })
);

La création du modèle commencera toujours par un appel à tf.sequential () . Le bloc de construction principal d'un modèle est constitué de couches. Nous pouvons nous connecter au modèle autant de couches du réseau neuronal que nécessaire. Ici, nous utilisons une couche dense , ce qui signifie que chaque neurone de la couche suivante a une connexion avec chaque neurone de la couche précédente. Par exemple, si nous avons deux couches denses, dans la première couche$$$N$ neurones, et dans le second - $$$M$, alors le nombre total de connexions entre les couches sera $$$NM$...

Dans notre cas, comme nous pouvons le voir, le réseau neuronal se compose d'une couche, dans laquelle il y a un neurone, donc les unités sont réglées sur un.



Aussi, pour la première couche du réseau neuronal, nous devons définir inputShape , puisque chaque instance d'entrée est représentée par un vecteur de deux valeurs X ₁ et X ₂ , donc inputShape = [2] . Notez qu'il n'est pas nécessaire de définir inputShape pour les couches intermédiaires - TensorFlow peut déterminer cette valeur à partir de la valeur des unités de la couche précédente.

De plus, si nécessaire, chaque couche peut se voir attribuer une fonction d'activation, nous avons déterminé ci-dessus qu'il s'agira d'une fonction sigmoïde. Les fonctions d'activation actuellement disponibles dans TensorFlow peuvent être trouvées ici .



Ensuite, nous devons compiler le modèle (voir API ici ), tandis que nous devons définir deux paramètres requis - c'est la fonction d'erreur et le type d'optimiseur qui recherchera son minimum:

model.compile({
    optimizer: tf.train.sgd(0.1),
    loss: 'meanSquaredError'
});

Nous définissons une descente de gradient stochastique avec un pas d'entraînement de 0,1 comme optimiseur.



La liste des optimiseurs implémentés dans la bibliothèque: tf.train.sgd , tf.train.momentum , tf.train.adagrad , tf.train.adadelta , tf.train.adam , tf.train.adamax , tf.train.rmsprop .  

En pratique, par défaut, vous pouvez immédiatement sélectionner l' optimiseur adam , qui a les meilleurs taux de convergence du modèle, contrairement à sgd - le taux d'apprentissage à chaque étape de la formation est défini en fonction de l'historique des étapes précédentes et n'est pas constant tout au long du processus d'apprentissage.

En tant que fonction d'erreur, elle est donnée par la fonction d'erreur quadratique moyenne:

$$

$$L=\frac{1}{N}\sum_{i=1}^{N}\left(y_{predicted(i)}-y_{expected(i)}\right)^2$$

Le modèle est défini et l'étape suivante est le processus d'entraînement du modèle, pour cela, la méthode d' ajustement doit être appelée sur le modèle :

async function initModel() {
    // skip for brevity

    await model.fit(trainingInputTensor, trainingOutputTensor, {
        epochs: 1000,
        shuffle: true,
        callbacks: {
            onEpochEnd: async (epoch, { loss }) => {
                // any actions on during any epoch of training
                await tf.nextFrame();
            }
        }
    })
}

Nous avons établi que le processus d'apprentissage devrait comprendre 100 étapes d'apprentissage (nombre d'époques d'apprentissage); également à chaque époque successive - les données d'entrée doivent être mélangées dans un ordre aléatoire ( shuffle = true ) - ce qui accélérera le processus de convergence du modèle, car il y a peu d'instances dans notre jeu de données d'entraînement (4).



Une fois le processus d'apprentissage terminé, nous pouvons utiliser la méthode prédire , qui, sur la base de nouveaux signaux d'entrée, calculera la valeur de sortie.

const testInput = generateInputs(10);
const testInputTensor = tf.tensor(testInput, [testInput.length, 2]);

const output = model.predict(testInputTensor).arraySync();

La méthode generateInputs génère simplement un exemple de jeu de données 10x10 qui divise le plan de coordonnées en 100 carrés:

$$

$$[[0,0], [0, 0.1], [0, 0.2], …. [1, 1]]$$

Dans la figure suivante, vous verrez une partie du processus d'apprentissage:









Simulation de l'opération logique XOR L'



ensemble d'apprentissage pour cette fonction est illustré à la Figure 6, et nous placerons également ces points comme nous l'avons fait pour l'opération logique OU sur le plan de coordonnées





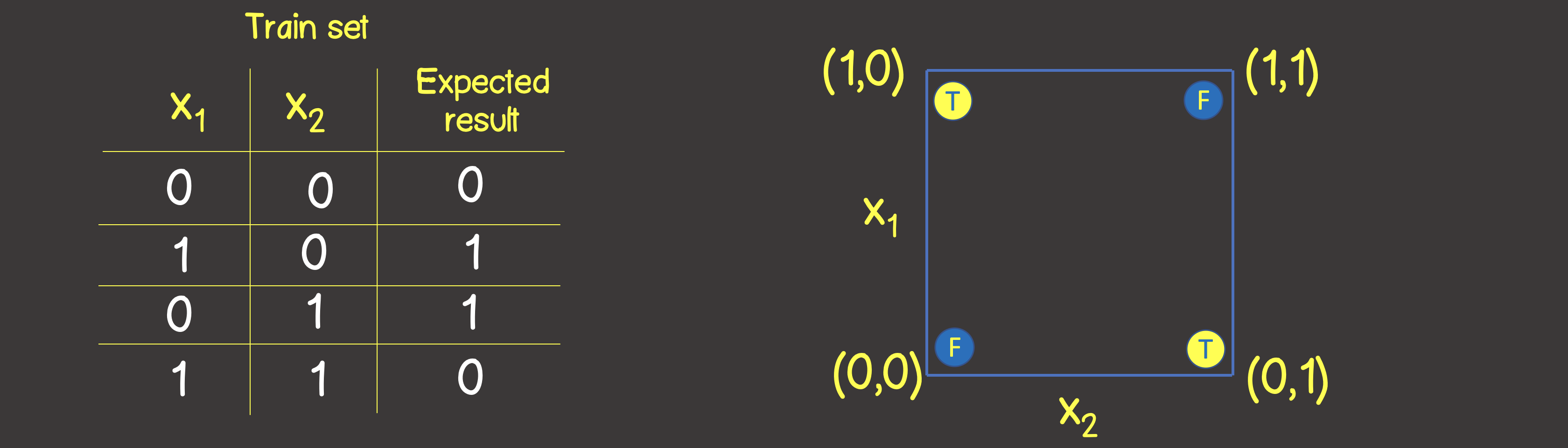
Figure 6 - Ensemble de données d'apprentissage et modèle pour la modélisation de l'opération logique OU EXCLUSIF (XOR)



Veuillez noter que contrairement à l'opération logique OU - vous ne pouvez pas diviser le plan avec une ligne droite, de sorte que d'un côté il y a toutes les valeurs VRAI , et de l'autre côté - toutes FAUX . Cependant, nous pouvons le faire en utilisant deux courbes (Figure 7).



De toute évidence, dans ce cas, un neurone dans une couche ne suffit pas - vous avez besoin d'au moins une couche supplémentaire avec deux neurones, dont chacun définirait l'une des deux lignes du plan.





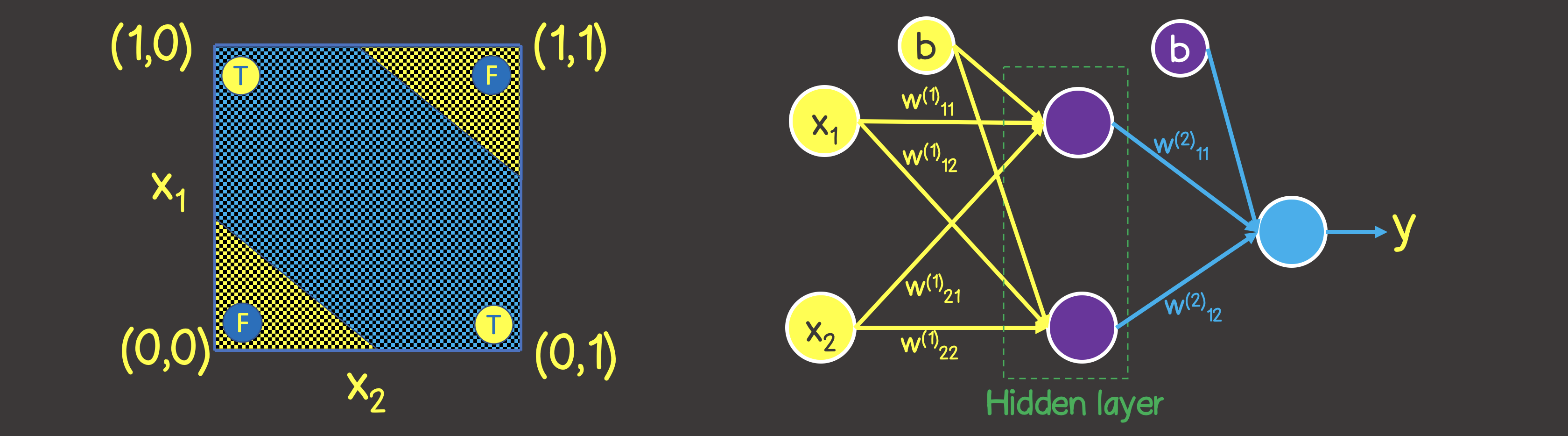
Figure 7 - Modèle de réseau neuronal pour l'opération logique OU EXCLUSIF (XOR)



Dans le code précédent, nous devons apporter des modifications à plusieurs endroits, dont l'un est le jeu de données d'entraînement lui-même:

const input = [[0, 0], [1, 0], [0, 1], [1, 1]];
const inputTensor = tf.tensor(input, [input.length, 2]);

const output = [[0], [1], [1], [0]]
const outputTensor = tf.tensor(output, [output.length, 1]);

La deuxième place est la structure modifiée du modèle, selon la figure 7:

model = tf.sequential();
model.add(
    tf.layers.dense({ inputShape: [2], units: 2, activation: 'sigmoid' })
);
model.add(
    tf.layers.dense({ units: 1, activation: 'sigmoid' })
);

Le processus d'apprentissage dans ce cas ressemble à ceci:









Sujet de l'article suivant



Dans le prochain article, nous décrirons comment résoudre les problèmes liés à la classification des objets en catégories, à partir d'une liste de quelques signes.