Python et théorie des ensembles

Python a un type de données très utile pour travailler avec des sets - set . Ce type de données, des exemples d'utilisation et un court extrait de la théorie des ensembles seront discutés plus tard.

Une réserve doit être faite tout de suite que cet article ne prétend en aucun cas à une rigueur et à une exhaustivité mathématiques, mais plutôt une tentative de démontrer de manière accessible des exemples d'utilisation d'ensembles dans le langage de programmation Python.

– , , , - , . :

– .

? , , .

, . , , .

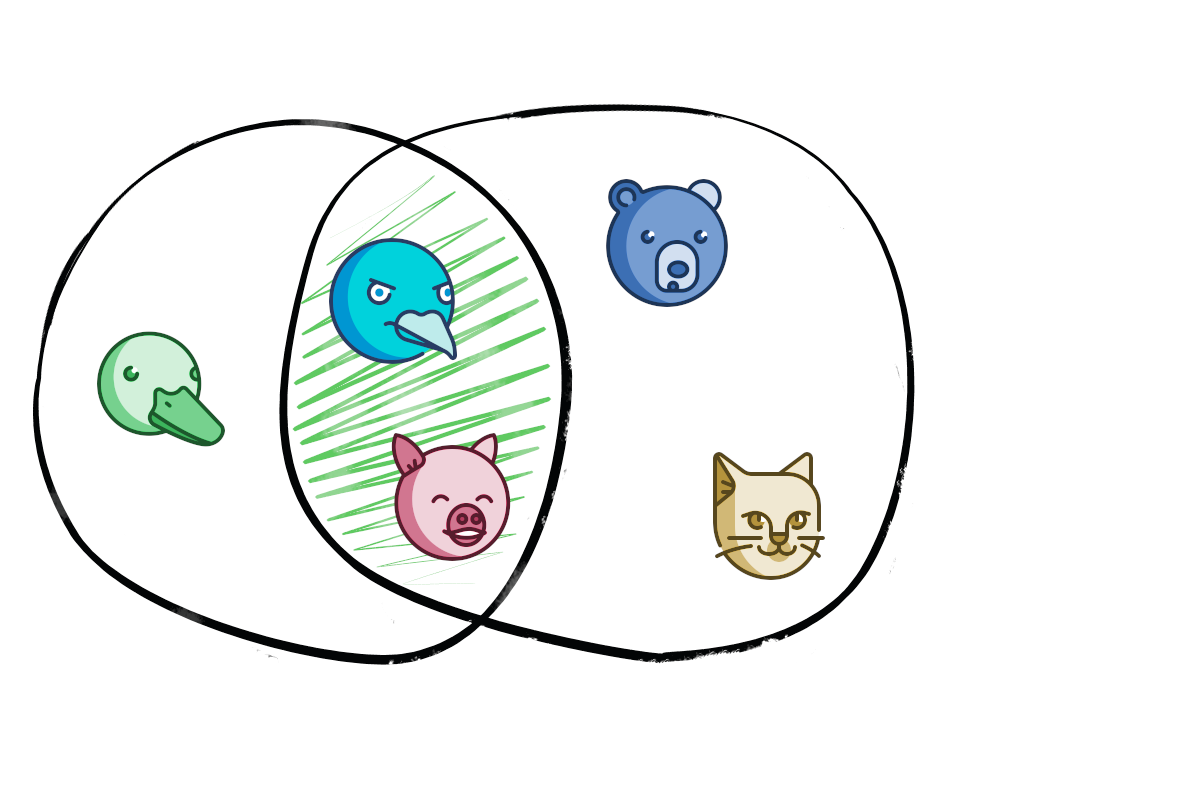
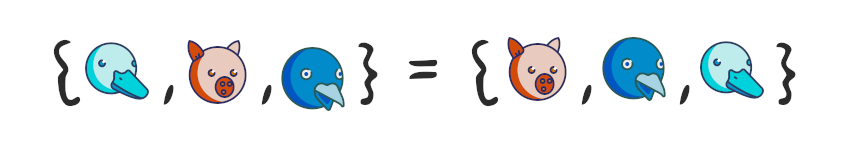
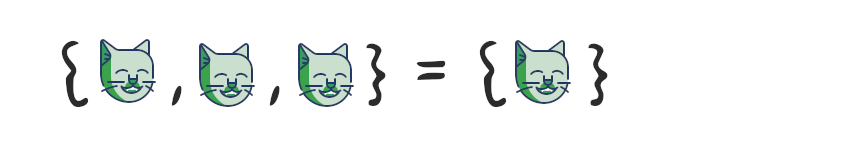
, , , – . , , . Python, .

Python

Python . – :

fruits = {"banana", "apple", "orange"}

, . :

wrong_empty_set = {}
print(type(wrong_empty_set))

# 
<class "dict">

set():

correct_empty_set = set()
print(type(correct_empty_set))

# 
<class "set">

set() - , (Iterable):

color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)

#  (   ):
{"red", "purple", "blue", "green"}

– set comprehension. , list comprehension ( ).

numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]

#      - 
#     
even_numbers = {
    number for number in numbers
    if number % 2 == 0
}
print(even_numbers)

#  (   ):
{2, 4, 6}

, ( ) Python (Hashable) . , set -. , – , . Python (int, float, str, bool, ..) – . , tuple, , .

#   (tuple)
records = {
    ("", 17_200_000), 
    ("-", 5_400_000), 
    ("", 1_600_000),
    ("", 17_200_000),
}

for city, population in records:
    print(city)

#  (   ):


-

. - , , .. "" .

class City:
    def __init__(self, name: str):
        self.name = name

    def __repr__(self) -> str:
        """   __repr__    
        """
        return f'City("{self.name}")'

print(City("Moscow") == City("Moscow"))

# :
False

cities = {City("Moscow"), City("Moscow")}
print(cities)

# 
{City("Moscow"), City("Moscow")}

, City("Moscow") , cities .

, City:

class City:
    def __init__(self, name: str):
        #  name   ,   
        #       
        self._name = name

    def __hash__(self) -> int:
        """   
        """
        return hash((self._name, self.__class__))

    def __eq__(self, other) -> bool:
        """    ( ==)
        """
        if not isinstance(other, self.__class__):
            return False
        return self._name == other._name

    def __repr__(self) -> str:
        """   __repr__    
        """
        return f'City("{self._name}")'

, :

moscow = City("Moscow")
moscow_again = City("Moscow")

print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# :
True

#        
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)

#  (   ):
{City("Kazan"), City("Moscow")}

set Python Collection ( ), :

iterable-

- in. . O(1) , -.

tremendously_huge_set = {"red", "green", "blue"}

if "green" in tremendously_huge_set:
    print("Green is there!")
else:
    print("Unfortunately, there is no green...")

# :
Green is there!

if "purple" in tremendously_huge_set:
    print("Purple is there!")
else:
    print("Unfortunately, there is no purple...")

# :
Unfortunately, there is no purple...

– , . .

even_numbers = {i for i in range(100) if i % 2 == 0}

#  
cardinality = len(even_numbers)
print(cardinality)

# :
50

, , , iterable-.

colors = {"red", "green", "blue"}

#        for
for color in colors:
    print(color)

#  (   ):
red
green
blue

#    ,   iterable-
color_counter = dict.fromkeys(colors, 1)
print(color_counter)

#  (   ):
{"green": 1, "red": 1, "blue": 1}

, . .

– , . , .

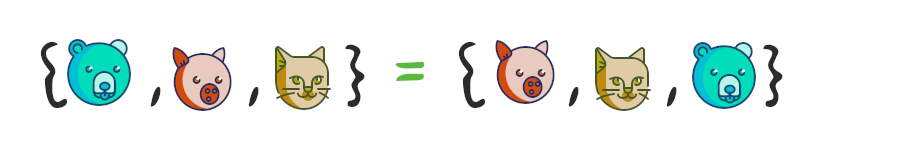
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)

# :
True

, , . , .

even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}

# ,        
if even_numbers.isdisjoint(odd_numbers):
    print("  !")

# :
  !

S – , S. S .

#     100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}

#     100
natural_numbers = set(range(100))

#       
#  
if fibonacci_numbers.issubset(natural_numbers):
    print("!")

# :
!

#       
#    
if natural_numbers.issuperset(fibonacci_numbers):
    print("!")

# :
!

empty = set()

#  issubset  issuperset    iterable-
print(
    empty.issubset(range(100))
    and empty.issubset(["red", "green", "blue"])
    and empty.issubset(set())
)

# :
True

natural_numbers = set(range(100))

if natural_numbers.issubset(natural_numbers):
    print("!")

# :
!

, .

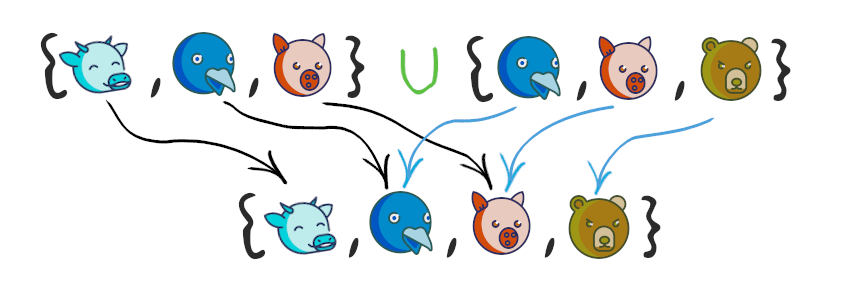
– , . Python , .

my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}

#       `|`,
#       set
our_fruits = my_fruits | your_fruits
print(our_fruits)

#  (   ):
{"apple", "banana", "orange", "pear"}

#     union.
#    ,   union   
#   set,   iterable-
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)

#  (   ):
{"apple", "banana", "orange", "pear"}

, , . O(1).

colors = {"red", "green", "blue"}

#  add     
colors.add("purple")
#  ,     ,  
#  
colors.add("red")
print(colors)

#  (   ):
{"red", "green", "blue", "purple"}

#  update  iterable- (, ,   ..)
#      
numbers = {1, 2, 3}
numbers.update(i**2 for i in [1, 2, 3])
print(numbers)

#  (   ):
{1, 2, 3, 4, 9}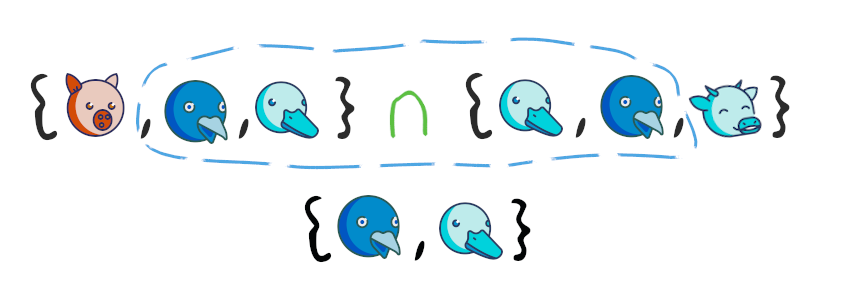

– , , .

def is_prime(number: int) -> bool:
    """  True,  number -   
    """
    assert number > 1
    return all(number % i for i in range(2, int(number**0.5) + 1))

def is_fibonacci(number: int) -> bool:
    """  True,  number -   
    """
    assert number > 1
    a, b = 0, 1
    while a + b < number:
        a, b = b, a + b
    return a + b == number

#     100
primes = set(filter(is_prime, range(2, 101)))

#     100
fibonacci = set(filter(is_fibonacci, range(2, 101)))

#     100,   
#  
prime_fibonacci = primes.intersection(fibonacci)

#    `&`,    
prime_fibonacci = fibonacci & primes

print(prime_fibonacci)

#  (   ):
{2, 3, 5, 13, 89}

& , set. intersection, , iterable-. , , intersection_update, intersection, -.

– , , .

i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
    "Go": 0.4, 
    "C++": 0.6, 
    "Rust": 0.2, 
    "Java": 0.9
}

#  ,   `-`  
#    set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)

#  (   ):
{"Rust", "C++"}

#  difference     iterable-,
#   dict, 
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)

# :
{"Python"}

, – . , , , . O(1).

fruits = {"apple", "orange", "banana"}

#    .   
#   ,    
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)

#  (   ):
{"apple", "banana"}

#  remove   discard,   ,
#      
fruits.remove("pineapple")  # KeyError: "pineapple"

differene_update, iterable- iterable-. difference, , .

numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers.difference_update(even_numbers_under_100)
print(numbers)

#  (   ):
{1, 3, 5, 7, 9}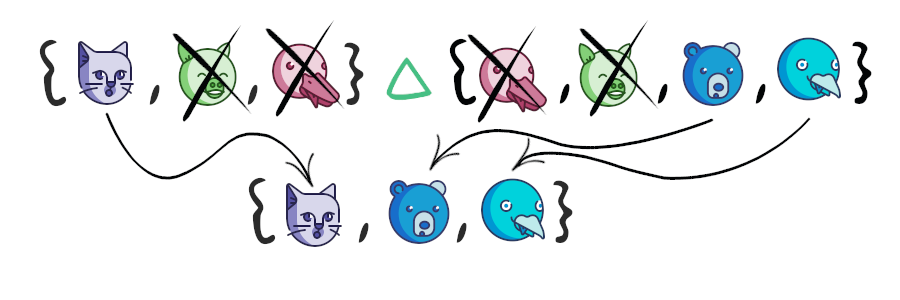

– , , . .

non_positive = {-3, -2, -1, 0}
non_negative = {0, 1, 2, 3}

#  ,   `^`  
#     set
non_zero = non_positive ^ non_negative
print(non_zero)

#  (   ):
{-1, -2, -3, 1, 2, 3}

, 0 , . , ^, – symmetric_difference symmetric_difference_update. iterable- , , symmetric_difference -, symmetric_difference_update .

non_positive = {-3, -2, -1, 0}
non_negative = range(4)

non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)

#  (   ):
{-1, -2, -3, 1, 2, 3}

#  symmetric_difference_update   
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)

#  (   ):
{"red", "yellow"}

Conclusion

J'espère avoir pu montrer que Python a de très bons outils intégrés pour travailler avec des ensembles. En pratique, cela permet souvent de réduire la quantité de code, de le rendre plus expressif et plus facile à comprendre, et donc plus maintenable. Je serai heureux si vous avez des commentaires et des ajouts constructifs.

Liens utiles

Ensembles (article Wikipedia)

Documentation de type pour les ensembles

Iterables (Glossaire Python)

Objets hachables (Glossaire Python)

Ensembles en Python

Set Theory: la méthode de la folie des bases de données

Python et théorie des ensembles

Python et théorie des ensembles

Python

Conclusion

Liens utiles

More articles: