En traduisant l'hypothèse de Keller dans un langage de recherche de graphes compréhensible par ordinateur, les chercheurs ont finalement résolu le problème de la couverture des espaces avec des tuiles.

Une équipe de mathématiciens a finalement compris l'hypothèse de Keller - mais pas de leur propre chef. Au lieu de cela, ils ont formé toute une flotte d'ordinateurs et ils l'ont résolu.
L'hypothèse de Keller, avancée il y a 90 ans par Ott-Heinrich Keller, est liée à la tâche de recouvrir des espaces avec des tuiles identiques. Elle fait valoir que si vous pavez un espace bidimensionnel avec des carreaux carrés bidimensionnels, au moins deux d'entre eux devront toucher les côtés complètement, et non partiellement. L'hypothèse fait la même prédiction pour toutes les dimensions - c'est-à-dire que lors du remplissage d'un espace à 12 dimensions avec des «carrés» à 12 dimensions, au moins deux d'entre eux doivent avoir un bord commun.
Pendant des années, les mathématiciens se sont battus sur cette hypothèse, prouvant sa vérité pour certaines dimensions et fausse pour d'autres. Et à l'automne dernier, la question n'était toujours pas résolue pour l'espace à sept dimensions.
Mais de nouvelles preuves générées par ordinateur ont également résolu ce problème. La preuve , publiée en octobre dernier, est l'un des exemples les plus récents de la combinaison du génie humain et de la puissance de calcul pure pour répondre aux questions les plus passionnantes en mathématiques.
Les auteurs du nouveau travail, Joshua Breukensik de Stanford, Marin Hijul et John Mackey de l'Université Carnegie Mellon, et David Narvaez de Rochester Institute of Technology, ont résolu ce problème en utilisant 40 ordinateurs. En seulement 30 minutes, les machines ont produit une réponse monosyllabique: oui, en sept dimensions, l'hypothèse est correcte. Et nous n'avons même pas à tirer cette conclusion sur la foi.
Attaché à la réponse est un long élément de preuve expliquant sa vérité. La preuve est trop longue à comprendre pour un humain, mais un autre programme informatique peut la vérifier.
En d'autres termes, même si nous ne savons pas exactement ce que les ordinateurs ont fait pour prouver l'hypothèse de Keller, nous pouvons au moins nous assurer qu'ils l'ont bien fait.
La septième dimension mystérieuse
Il est facile de voir que la conjecture de Keller est vraie en deux dimensions. Prenez un morceau de papier et essayez de le recouvrir de carrés égaux sans espace ni chevauchement. Bientôt, vous vous rendrez compte que vous ne pouvez le faire que si au moins deux carrés ont le même côté. Si vous avez des cubes sous la main, il vous sera facile de vérifier que l'hypothèse est vraie pour la troisième dimension. En 1930, Keller a suggéré que cette relation fonctionne pour toutes les dimensions et leurs carreaux correspondants.
Les premiers résultats ont soutenu la prédiction de Keller. En 1940, Oscar Perron a prouvé que l'hypothèse était correcte pour les mesures un à six. Cependant, plus de 50 ans plus tard, une nouvelle génération de mathématiciens a trouvé le premier contre-exemple à cette hypothèse: en 1992, Jeffrey Lagarias et Peter Shoreprouvé que l'hypothèse ne fonctionne pas dans la 10e dimension.

L'hypothèse de Keller prédit que lors du remplissage d'un espace dans n'importe quelle dimension, au moins deux tuiles doivent toucher complètement les côtés.
Lors du remplissage d'un espace bidimensionnel, de nombreux carreaux ont des côtés communs (lignes bleues).
Lors du remplissage de l'espace 3D, de nombreux cubes ont des faces communes (bleu).
Il est facile de montrer que si une hypothèse échoue dans une certaine dimension, elle ne tient pas dans toutes les plus élevées. Par conséquent, après les travaux de Lagarias et Shor, il ne reste plus qu'à résoudre le problème pour les septième, huitième et neuvième dimensions. En 2002, Mackey a prouvé que l'hypothèse de Keller était fausse pour la dimension huit (et donc neuf).
Seule la septième dimension est restée ouverte - c'était soit la plus grande dimension pour laquelle cette hypothèse est vraie, soit la plus petite dans laquelle l'hypothèse est incorrecte.
«Personne ne sait exactement ce qui se passe là-bas», a déclaré Khiyul.
Relier les points
Alors que les mathématiciens se sont débattus avec ce problème pendant plusieurs décennies, leurs méthodes ont progressivement changé. Perron a travaillé sur les six premières dimensions en utilisant uniquement un crayon et du papier, mais dans les années 1990, les chercheurs avaient trouvé comment traduire l'hypothèse de Keller sous une forme complètement différente - leur permettant d'utiliser des ordinateurs pour la résoudre.
La formulation originale de la conjecture de Keller concerne l'espace continu lisse. Dans un tel espace, il existe un nombre infini de façons de placer un nombre infini de tuiles. Mais les ordinateurs ne sont pas bons pour résoudre des problèmes avec un nombre infini d'options - pour y faire face, ils ont besoin d'objets discrets et finis.

Marin Hijul de l'Université Carnegie Mellon
En 1990, Kereszteli Korradi et Sandor Shabo ont proposé un objet discret approprié. Ils ont montré que des questions équivalentes à l'hypothèse de Keller peuvent être posées sur cet objet. Et si vous prouvez quelque chose lié à ces objets, alors l'hypothèse de Keller sera prouvée. Cela a réduit la question de l'infini à un problème arithmétique moins complexe avec des nombres multiples.
Voici comment cela fonctionne.
Supposons que vous souhaitiez traiter l'hypothèse de Keller en deux dimensions. Corradi et Shabo ont proposé une méthode pour cela, en utilisant la construction d'une structure, qu'ils ont appelée le graphe de Keller.
Pour commencer, imaginez qu'il y ait 16 dés sur la table, et tous ont un bord supérieur avec deux points (deux points désignent un espace bidimensionnel, et pourquoi il y a 16 cubes - nous verrons un peu plus tard). Tous les cubes sont tournés de la même manière, de sorte que deux points sont situés de la même manière pour tout le monde. Colorez chaque point avec l'une des quatre couleurs suivantes: rouge, vert, blanc ou noir.
Les points d'un cube ne changent pas de place - laissez l'un d'eux désigner la coordonnée x et l'autre - y. Après avoir coloré les cubes, nous commencerons à dessiner des lignes, ou des arêtes, entre des paires de cubes si deux conditions sont remplies: les points au même endroit pour une paire de cubes ont des couleurs différentes, et dans l'autre ils sont différents et appariés, et le rouge et le vert sont considérés comme des paires, ou du noir avec du blanc.
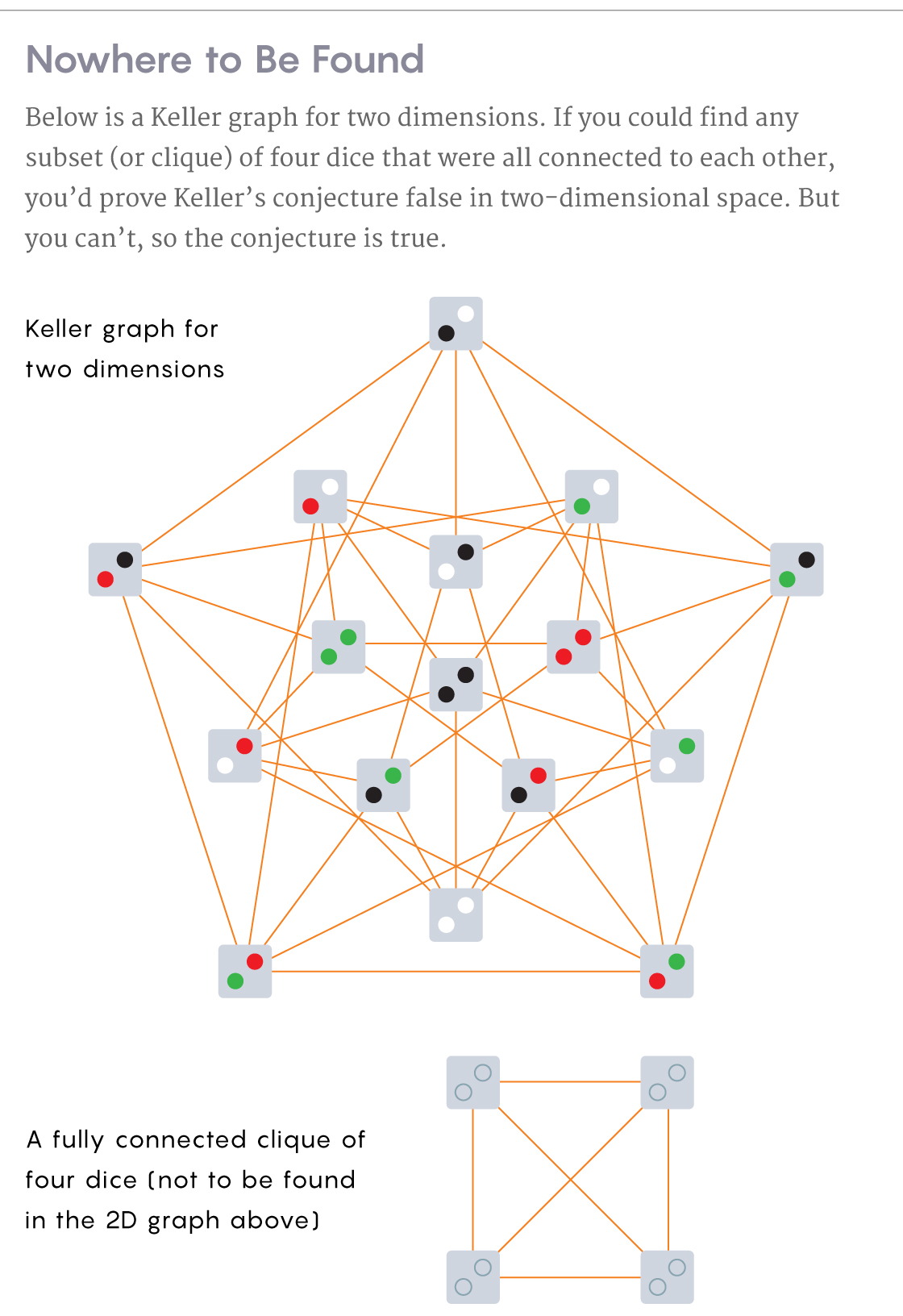
Graphique de Keller pour deux dimensions. En trouvant un sous-ensemble de quatre cubes dans lesquels chacun est connecté à tous les autres, vous réfuterez l'hypothèse de Keller pour l'espace bidimensionnel. Cependant, un tel sous-ensemble n'existe pas et l'hypothèse est correcte.
Vous trouverez ci-dessous un exemple d'une clique entièrement fusionnée de quatre dés qui ne figure pas dans le graphique.
Autrement dit, par exemple, si un cube a deux points rouges et l'autre a deux points noirs, ils ne sont pas reliés par une arête. Leurs points aux mêmes positions ont des couleurs différentes, mais ils ne satisfont pas à l'exigence d'appariement des couleurs. Si un cube a des points rouges et noirs et que l'autre a deux points verts, ils sont reliés par un bord, car dans une position, ils ont des couleurs appariées (rouge et vert), et dans l'autre, ils sont simplement différents (noir et vert).
Il y a 16 façons de colorer deux points avec quatre couleurs (nous avons donc 16 cubes). Présentez toutes ces 16 possibilités devant vous. Connectez toutes les paires de cubes qui satisfont aux exigences. Y a-t-il quatre cubes dans votre schéma, chacun étant combiné avec trois autres?
Un tel sous-ensemble de cubes entièrement connecté est appelé une clique. Si vous pouvez en trouver un, vous réfuterez l'hypothèse de Keller en deux dimensions. Cependant, vous ne pouvez pas - cela n'existe tout simplement pas. Et l'absence d'une telle clique de quatre cubes signifie que l'hypothèse de Keller est vraie pour deux dimensions.
Ces cubes ne sont pas littéralement les mêmes tuiles que l'hypothèse de Keller, cependant, vous pouvez supposer que chaque cube représente une tuile. Considérez les couleurs attribuées aux points comme les coordonnées qui placent le cube dans l'espace. Et l'existence d'un bord est une description de la façon dont deux cubes sont positionnés l'un par rapport à l'autre.
Si les couleurs des cubes sont les mêmes, elles représentent des tuiles également espacées. S'ils n'ont pas de couleurs et de paires de couleurs communes (l'une a le noir et le blanc, l'autre le vert et le rouge), ils indiquent des carreaux qui se chevauchent partiellement - ce qui n'est pas autorisé pour remplir l'espace. Si deux cubes ont un ensemble de couleurs correspondantes et un ensemble de la même couleur (l'un rouge-noir, l'autre vert-noir), ils représentent des tuiles avec un côté commun.
Enfin, et surtout - s'ils ont un ensemble de couleurs appariées et un autre ensemble de couleurs différentes - c'est-à-dire s'ils sont reliés par un bord - alors les cubes représentent des carreaux qui sont en contact les uns avec les autres, mais légèrement décalés, en raison desquels leurs bords ne coïncident pas complètement ... C'est cette condition que nous devons étudier. Les cubes reliés par un bord désignent des tuiles contiguës qui n'ont pas de côté commun - c'est exactement la disposition nécessaire pour réfuter l'hypothèse de Keller.
"Ils devraient toucher, mais pas complètement", a déclaré Khiyul.

Même coloration - même arrangement.
Différentes couleurs, pas de paires - se chevauchent.
Deux couleurs appariées et une paire des mêmes sont le côté commun.
Deux couleurs appariées et deux différentes - contact partiel par les côtés.
Mise à l'échelle
Il y a trente ans, Corradi et Shabo ont prouvé que les mathématiciens pouvaient utiliser une procédure similaire pour travailler avec l'hypothèse de Keller dans n'importe quelle dimension, en modifiant les paramètres de l'expérience. Pour prouver l'hypothèse de Keller en trois dimensions, vous pouvez utiliser 216 cubes avec trois points sur le bord, et éventuellement trois paires de couleurs (cependant, il y a une certaine flexibilité ici). Ensuite, vous devez rechercher huit cubes (2 3 ), complètement connectés les uns aux autres, selon les mêmes conditions que nous avons données ci-dessus.
En général, pour prouver la conjecture de Keller en n dimensions, vous devez utiliser des cubes avec n points et essayer de trouver une clique de taille 2 n parmi eux . On peut supposer qu'il représente une sorte de super-tuile (constituée de 2 ncarreaux plus petits) capables de couvrir tout l'espace à n dimensions.
Si vous pouvez trouver cette super-tuile (qui n'a pas de tuiles avec un côté commun), vous pouvez en utiliser des copies pour couvrir tout l'espace avec des tuiles sans côté commun, ce qui réfute l'hypothèse de Keller.
«En cas de succès, vous pouvez couvrir tout l'espace de transfert. Un bloc sans côtés de carreaux communs s'étendra sur tout le sol », a déclaré Lagarias, maintenant à l'Université du Michigan.
Mackey a réfuté l'hypothèse de Keller dans la 8e dimension, trouver une clique de 256 cubes (2 8 ), il restait à faire face à l'hypothèse de la 7e dimension, trouver une clique de 128 cubes (2 7). Trouver cette clique réfutera l'hypothèse de Keller dans la septième dimension. Prouvez qu'il n'existe pas et vous prouverez que l'hypothèse est vraie.
Malheureusement, trouver une clique de 128 cubes est une tâche particulièrement difficile. Dans des travaux antérieurs, les chercheurs ont profité du fait que les dimensions 8 et 10 peuvent, en un sens, être «décomposées» en espaces de dimension inférieure, avec lesquels il est plus facile de travailler. Et ici, cela n'a pas fonctionné.
"La septième dimension n'est pas pratique car 7 est un nombre premier et vous ne pouvez pas le décomposer en dimensions d'un ordre plus petit", a déclaré Lagarias. "Par conséquent, il n'y avait pas d'autre issue que de traiter la combinatoire à part entière de ces graphiques."
Trouver une clique de 128 cubes peut être difficile pour le cerveau sans aide - mais ce sont les types de questions auxquelles les ordinateurs sont capables de répondre, surtout avec un peu d'aide.
Le langage de la logique
Pour transformer la recherche de clics en une tâche qu'un ordinateur peut gérer, vous devez la formuler en termes de logique propositionnelle . C'est un raisonnement si logique, qui comprend un ensemble de restrictions.
Disons que vous planifiez une fête avec des amis. Vous essayez de créer une liste d'invités, mais il y a des conflits d'intérêts. Supposons que vous souhaitiez soit inviter Alexei, soit exclure Kolya. Un de vos amis veut inviter Kolya, ou Vlad, ou les deux. Un autre ami ne veut appeler ni Alexei ni Vlad. Avec de telles restrictions, est-il possible de créer une liste d'invités qui satisfera les trois?
En termes informatiques, ce problème est appelé le problème d'acceptabilité. Il peut être résolu en décrivant la condition dans la formule propositionnelle. Dans ce cas, cela ressemble à ceci, et A, K et B désignent des invités potentiels: (A OU PAS K) ET (K OU B) ET (PAS A OU PAS B).
L'ordinateur le calcule en remplaçant chaque variable par 0 ou 1. 0 est la valeur de la variable «faux» ou désactivé, et 1 est «vrai» ou activé. En remplaçant 0 au lieu de A, nous disons qu'Alexei n'a pas été invité et 1 qu'il a été invité. Dans cette formule simple, 0 et 1 peuvent être remplacés (en créant une liste d'invités) de plusieurs façons, et il est possible qu'après les avoir parcourus, tout l'ordinateur conclura qu'il est impossible de satisfaire tous les intérêts. Cependant, dans ce cas, il existe deux façons de substituer 1 et 0 pour plaire à tout le monde: A = 1, K = 1, B = 0 (inviter Alexei et Kolya) et A = 0, K = 0, B = 1 (inviter un Vlad ).
Le programme informatique qui résout de telles déclarations est appelé le solveur SAT, où SAT est l'abréviation de satisfiability. Il examine toutes les combinaisons de variables et donne une réponse monosyllabique - soit OUI, il existe un moyen de satisfaire aux exigences de la formule, soit NON, ce n'est pas le cas.

John Mackie de l'Université Carnegie Mellon
"Vous cherchez simplement à voir si vous pouvez attribuer des valeurs vraies et fausses à toutes les variables afin que la formule entière soit vraie, et si oui, alors elle est satisfaite, et sinon, alors non", a déclaré Thomas Hales de Université de Pittsburgh.
La question de trouver une clique de 128 cubes est un problème similaire. Il peut également être réécrit sous forme de formule propositionnelle et donné au solveur SAT. Commencez avec beaucoup de dés avec 7 points chacun et 6 couleurs possibles. Est-il possible de colorer les points pour que 128 cubes soient connectés les uns aux autres selon certaines règles? En d'autres termes, est-il possible d'attribuer des couleurs pour que le clic apparaisse?
La formule propositionnelle de la question cliquée est assez longue et contient 39 000 variables. Chacun peut se voir attribuer l'une des deux valeurs, 0 ou 1. En conséquence, le nombre d'options possibles pour organiser les valeurs ou les méthodes d'attribution des couleurs était de 2,39 000 - ce qui est très, très bien.
Pour trouver la réponse à la question sur l'hypothèse de Keller en sept dimensions, l'ordinateur devrait vérifier toutes ces combinaisons - et soit les exclure toutes (ce qui signifierait que la clique de taille 128 n'existe pas, et l'hypothèse de Keller dans la septième dimension est correcte), soit trouver au moins serait une option de travail (réfutant l'hypothèse de Keller).
«Si vous faites une simple itération de toutes les possibilités, vous tombez sur un nombre à 324 chiffres», a déclaré Mackey. L'ordinateur le plus rapide du monde fonctionnerait jusqu'à la fin des temps, passant par toutes les possibilités.
Cependant, les auteurs du nouveau travail ont compris comment un ordinateur peut donner une réponse définitive sans vérifier toutes les possibilités. La clé de tout cela est l'efficacité.
Efficacité cachée
Mackey se souvient du jour où, de son point de vue, le projet a réellement commencé à fonctionner. Il se tenait devant un tableau noir dans son bureau de l'Université Carnegie Mellon, discutant d'un problème avec deux coauteurs, Hijul et Breikensik, lorsque Hijul a proposé un moyen de structurer la recherche afin qu'elle puisse être achevée dans un délai raisonnable.
«Il y avait un vrai génie humain qui travaillait dans mon bureau ce jour-là», a déclaré Mackey. - J'étais comme regarder Wayne Gretzky ou LeBron James en finale de la NBA. J'ai la chair de poule rien que par le souvenir. "
Vous pouvez personnaliser les recherches pour un graphique Keller spécifique de différentes manières. Imaginez que vous avez beaucoup de cubes sur votre table et que vous essayez d'en résoudre 128, en suivant les règles du comte Keller. Disons que vous avez sélectionné 12 correctement, mais que vous ne savez pas comment ajouter le suivant. À ce stade, vous pouvez supprimer toute configuration de 128 dés qui inclut cette configuration non fonctionnelle de 12.
«Si vous savez que vos cinq premières affectations ne correspondent pas, vous n'avez pas besoin de rechercher d'autres variables, et cela réduit généralement beaucoup le champ de recherche», a déclaré Shore, maintenant au MIT.
Un autre type d'efficacité est associé à la symétrie. Les objets symétriques sont un peu les mêmes. L'identité nous permet de comprendre l'objet dans son ensemble, en n'en étudiant qu'une partie - en regardant la moitié du visage d'une personne, vous pouvez le restaurer entièrement.
De même, vous pouvez couper les coins ronds dans le cas des graphiques Keller. Imaginez à nouveau que vous essayez d'aligner les cubes sur la table. Disons que vous commencez au centre de la table et que vous construisez votre main sur la gauche. Vous posez quatre dés et vous vous retrouvez dans une impasse. Vous avez maintenant éliminé une combinaison de départ et toutes les combinaisons basées sur elle. Cependant, vous pouvez exclure la mise en miroir de cette combinaison initiale - la configuration des cubes que vous obtenez si vous les placez de la même manière, uniquement sur la droite.
«Si vous avez trouvé un moyen de résoudre des problèmes satisfaisants qui tient intelligemment compte de la symétrie, vous avez grandement simplifié la tâche», a déclaré Hales.
Quatre collègues ont profité de l'efficacité de cette recherche d'une nouvelle manière - en particulier, ils ont automatisé la prise en compte des cas symétriques, alors que les mathématiciens les traitaient auparavant presque à la main.
En conséquence, ils ont tellement amélioré leur recherche de cliques de taille 128 qu'au lieu de vérifier 2,39 000 configurations, leur programme n'a dû vérifier qu'environ un milliard ( 2,30 ). Cela a fait une recherche qui pourrait prendre une éternité dans une tâche pour une matinée. Enfin, après seulement une demi-heure de calculs, ils ont reçu une réponse.
"Les ordinateurs ont dit non, donc nous savons que l'hypothèse fonctionne", a déclaré Hiyul. Il est impossible de colorer les 128 cubes de manière à ce qu'ils fusionnent tous, donc l'hypothèse de Keller pour la septième dimension est confirmée. Pour tout placement de carreaux couvrant un espace, il y aura inévitablement au moins une paire de bords complètement touchants.
L'ordinateur n'a pas donné simplement une réponse monosyllabique. Il y a joint une longue preuve de 200 Go à l'appui de cette conclusion.
La preuve n'est pas simplement un calcul de tous les ensembles de variables qui ont été vérifiés par un ordinateur. C'est un argument logique prouvant que la clique nécessaire ne peut exister. Les chercheurs ont introduit les preuves dans un programme qui teste les preuves formelles en traçant la logique d'un argument et en le validant.
«Nous n'avons pas simplement passé en revue toutes les options et n'avons rien trouvé. Nous avons examiné toutes les options et avons pu noter la preuve qu'une telle chose n'existe pas, - a déclaré Mackey. "Nous avons pu noter les preuves d'insatisfaction."