Voyons quelles solutions ce problème a.
Répartition des objets "par capacité"
Afin de ne pas nous plonger dans des abstractions inintéressantes, nous la considérerons à l'aide de l'exemple d'une tâche spécifique - la surveillance . Je suis sûr que vous serez en mesure de relier par vous-même les méthodes proposées à vos tâches spécifiques.
Objets de surveillance "équivalents"
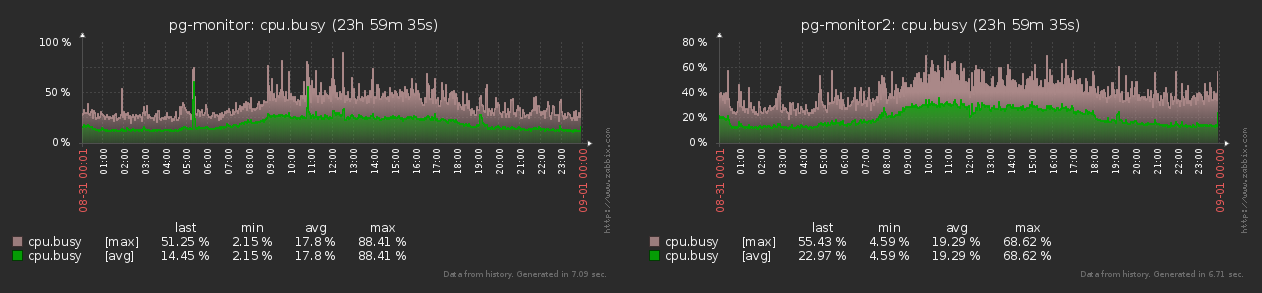
Un exemple est nos collecteurs de métriques pour Zabbix , qui partagent historiquement une architecture commune avec les collecteurs de journaux PostgreSQL. En effet
, chaque objet de surveillance (hôte) génère pour zabbix presque de manière stable le même ensemble de métriques avec la même fréquence tout le temps:
Comme vous pouvez le voir sur le graphique, la différence entre les valeurs min-max du nombre de métriques générées ne dépasse pas 15% . Par conséquent, nous pouvons considérer tous les objets comme égaux dans les mêmes «perroquets» .
Fort "déséquilibre" entre les objets
Contrairement au modèle précédent, les hôtes surveillés sont loin d'être homogènes pour les collecteurs de journaux .
Par exemple, un hôte peut générer un million de plans par jour dans le journal, un autre des dizaines de milliers et certains, même quelques-uns. Et les plans eux-mêmes sont très différents en termes de volume et de complexité et en termes de répartition au cours de la journée. Il s'avère donc que la charge "tremble" fortement , parfois:

Eh bien, puisque la charge peut tellement changer, vous devez apprendre à la gérer ...
Coordinateur
Nous comprenons immédiatement que nous devons évidemment mettre à l' échelle le système de collecteur, puisqu'un nœud séparé avec toute la charge ne fera plus face un jour. Et pour cela, nous avons besoin d'un coordinateur - quelqu'un qui gérera tout le zoo.
Il s'avère quelque chose comme ceci:

Chaque travailleur sa charge "en perroquets" et en pourcentage de la CPU réinitialise périodiquement le maître, ceux - au collecteur. Et il, sur la base de ces données, peut émettre une commande telle que "mettre un nouvel hôte sur un travailleur déchargé n ° 4" ou "hostA doit être transféré vers le travailleur n ° 3" .
Ici, vous devez également vous rappeler que, contrairement aux objets de surveillance, les collecteurs eux - mêmes n'ont pas du tout la même «puissance» - par exemple, sur l'un, vous pouvez avoir 8 cœurs de processeur, et sur l'autre - seulement 4, et même une fréquence inférieure. Et si vous les chargez avec des tâches "également", alors le second commencera à "se taire", et le premier sera inactif. D'où il suit ...
Tâches du coordinateur
En fait, il n'y a qu'une seule tâche: assurer la répartition la plus uniforme de la charge totale (en% cpu) entre tous les travailleurs disponibles. Si nous pouvons le résoudre parfaitement, alors l'uniformité de la distribution% cpu-load sur les collecteurs sera obtenue «automatiquement».
Il est clair que même si chaque objet génère la même charge, au fil du temps, certains d'entre eux peuvent "mourir", et de nouveaux apparaissent. Par conséquent, vous devez être capable de gérer l'ensemble de la situation de manière dynamique et de maintenir un équilibre en permanence .
Équilibrage dynamique
Nous pouvons résoudre un problème simple (zabbix) assez trivialement:
- on calcule la capacité relative de chaque collecteur "en tâches"
- répartissez toutes les tâches entre eux proportionnellement
- nous répartissons uniformément entre les travailleurs

Mais que faire en cas d'objets "fortement inégaux", comme pour un collecteur de journaux? ..
Évaluation de l'uniformité
Ci-dessus, nous avons utilisé le terme « distribution uniformément maximale » tout le temps , mais comment comparer formellement deux distributions, laquelle est «la plus uniforme»?
Pour évaluer l'uniformité en mathématiques, il existe depuis longtemps l' écart type . Qui est paresseux pour lire:
S[X] = sqrt( sum[ ( x - avg[X] ) ^ 2 of X ] / count[X] )Étant donné que le nombre de travailleurs sur chacun des collecteurs peut également différer pour nous, la répartition de la charge doit être normalisée non seulement entre eux, mais également entre les collecteurs dans leur ensemble .
Autrement dit, la répartition de la charge sur les travailleurs des deux collecteurs
[ (10%, 10%, 10%, 10%, 10%, 10%) ; (20%) ]n'est pas non plus très bonne, car le premier se révèle être 10% et le second - 20% , ce qui, pour ainsi dire, est deux fois plus élevé en termes relatifs.
Par conséquent, nous introduisons une seule métrique-distance pour une estimation générale de "l'uniformité":
d([%wrk], [%col]) = sqrt( S[%wrk] ^ 2 + S[%col] ^ 2 )La modélisation
Si nous avions quelques objets, alors nous pourrions les «décomposer» par force brute entre les ouvriers afin que la métrique soit minimale . Mais nous avons des milliers d'objets, donc cette méthode ne fonctionnera pas. Mais nous savons que le collecteur est capable de "déplacer" un objet d'un travailleur à un autre - modélisons cette option en utilisant la méthode de descente de gradient .
Il est clair que nous ne trouvons peut-être pas le minimum «idéal» de la métrique, mais le local est certain. Et la charge elle-même peut tellement varier dans le temps qu'il n'est absolument pas nécessaire de rechercher un «idéal» pendant un temps infini .
Autrement dit, nous devons simplement déterminer quel objet et vers quel travailleur il est le plus efficace de "déplacer". Et faisons-en une modélisation exhaustive triviale:
- ( host, worker)
- host worker' «»
«» . - « »
- d «»
Nous alignons toutes les paires dans l'ordre croissant de la métrique . Idéalement, nous devrions toujours implémenter le transfert de la première paire , car il donne la métrique cible minimale. Malheureusement, en réalité, le processus de transfert lui-même "coûte des ressources", vous ne devriez donc pas l'exécuter pour le même objet plus souvent qu'un certain intervalle de "refroidissement" .
Dans ce cas, nous pouvons prendre le deuxième, le troisième, ... par le rang de la paire - si seule la métrique cible diminue par rapport à la valeur actuelle.
S'il n'y a nulle part où diminuer - ici c'est un minimum local!
Exemple dans l'image:

Il n'est pas du tout nécessaire de démarrer les itérations «à fond». Par exemple, vous pouvez effectuer une analyse de charge moyenne sur un intervalle d'une minute et, une fois terminé, effectuer un seul transfert.
Micro-optimisations
Il est clair qu'un algorithme complexe
T() x W()n'est pas très bon. Mais dans ce document, vous ne devez pas oublier d'appliquer des optimisations plus ou moins évidentes qui peuvent parfois l'accélérer.
Zéro "perroquet"
Si un objet / une tâche / un hôte a généré une charge de "0 pièces" sur l'intervalle mesuré , alors ce n'est pas quelque chose qui peut être déplacé quelque part - il n'a même pas besoin d'être considéré et analysé.
Transfert automatique
Lors de la génération de paires, il n'est pas nécessaire d'évaluer l'efficacité du transfert d'un objet vers le même travailleur , là où il se trouve déjà . Après tout, ce sera déjà
T x (W - 1)- une bagatelle, mais sympa!
Charge indiscernable
Puisque nous modélisons le transfert de la charge et que l'objet n'est qu'un outil, il est inutile d' essayer de transférer le «même»% cpu - les valeurs des métriques resteront exactement les mêmes, bien que pour une distribution d'objets différente.
Autrement dit, il suffit d'évaluer un seul modèle pour le tuple (wrkSrc, wrkDst,% cpu) . Eh bien, et vous pouvez considérer «égal», par exemple, les valeurs% cpu qui correspondent jusqu'à 1 décimale.
Exemple d'implémentation JavaScript
var col = {
'c1' : {
'wrk' : {
'w1' : {
'hst' : {
'h1' : 5
, 'h2' : 1
, 'h3' : 1
}
, 'cpu' : 80.0
}
, 'w2' : {
'hst' : {
'h4' : 1
, 'h5' : 1
, 'h6' : 1
}
, 'cpu' : 20.0
}
}
}
, 'c2' : {
'wrk' : {
'w1' : {
'hst' : {
'h7' : 1
, 'h8' : 2
}
, 'cpu' : 100.0
}
, 'w2' : {
'hst' : {
'h9' : 1
, 'hA' : 1
, 'hB' : 1
}
, 'cpu' : 50.0
}
}
}
};
// ""
let $iv = (obj, fn) => Object.values(obj).forEach(fn);
let $mv = (obj, fn) => Object.values(obj).map(fn);
// initial reparse
for (const [cid, c] of Object.entries(col)) {
$iv(c.wrk, w => {
w.hst = Object.keys(w.hst).reduce((rv, hid) => {
if (typeof w.hst[hid] == 'object') {
rv[hid] = w.hst[hid];
return rv;
}
// ,
if (w.hst[hid]) {
rv[hid] = {'qty' : w.hst[hid]};
}
return rv;
}, {});
});
c.wrk = Object.keys(c.wrk).reduce((rv, wid) => {
// ID -
rv[cid + ':' + wid] = c.wrk[wid];
return rv;
}, {});
}
//
let S = col => {
let wsum = 0
, wavg = 0
, wqty = 0
, csum = 0
, cavg = 0
, cqty = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += w.cpu;
wqty++;
});
csum += c.cpu;
cqty++;
});
wavg = wsum/wqty;
wsum = 0;
cavg = csum/cqty;
csum = 0;
$iv(col, c => {
$iv(c.wrk, w => {
wsum += (w.cpu - wavg) ** 2;
});
csum += (c.cpu - cavg) ** 2;
});
return [Math.sqrt(wsum/wqty), Math.sqrt(csum/cqty)];
};
// -
let distS = S => Math.sqrt(S[0] ** 2 + S[1] ** 2);
//
let iterReOrder = col => {
let qty = 0
, max = 0;
$iv(col, c => {
c.qty = 0;
c.cpu = 0;
$iv(c.wrk, w => {
w.qty = 0;
$iv(w.hst, h => {
w.qty += h.qty;
});
w.max = w.qty * (100/w.cpu);
c.qty += w.qty;
c.cpu += w.cpu;
});
c.cpu = c.cpu/Object.keys(c.wrk).length;
c.max = c.qty * (100/c.cpu);
qty += c.qty;
max += c.max;
});
$iv(col, c => {
c.nrm = c.max/max;
$iv(c.wrk, w => {
$iv(w.hst, h => {
h.cpu = h.qty/w.qty * w.cpu;
h.nrm = h.cpu * c.nrm;
});
});
});
// ""
console.log(S(col), distS(S(col)));
//
let wrk = {};
let hst = {};
for (const [cid, c] of Object.entries(col)) {
for (const [wid, w] of Object.entries(c.wrk)) {
wrk[wid] = {
wid
, cid
, 'wrk' : w
, 'col' : c
};
for (const [hid, h] of Object.entries(w.hst)) {
hst[hid] = {
hid
, wid
, cid
, 'hst' : h
, 'wrk' : w
, 'col' : c
};
}
}
}
// worker
let move = (col, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
let wsrc = col[h.cid].wrk[h.wid]
, wdst = col[w.cid].wrk[w.wid];
wsrc.cpu -= h.hst.cpu;
wsrc.qty -= h.hst.qty;
wdst.qty += h.hst.qty;
// "" CPU
if (h.cid != w.cid) {
let csrc = col[h.cid]
, cdst = col[w.cid];
csrc.qty -= h.hst.qty;
csrc.cpu -= h.hst.cpu/Object.keys(csrc.wrk).length;
wsrc.hst[hid].cpu = h.hst.cpu * csrc.nrm/cdst.nrm;
cdst.qty += h.hst.qty;
cdst.cpu += h.hst.cpu/Object.keys(cdst.wrk).length;
}
wdst.cpu += wsrc.hst[hid].cpu;
wdst.hst[hid] = wsrc.hst[hid];
delete wsrc.hst[hid];
};
// (host, worker)
let moveCheck = (orig, hid, wid) => {
let w = wrk[wid]
, h = hst[hid];
// -
if (h.wid == w.wid) {
return;
}
let col = JSON.parse(JSON.stringify(orig));
move(col, hid, wid);
return S(col);
};
// (hsrc,hdst,%cpu)
let checked = {};
// ( -> )
let moveRanker = col => {
let currS = S(col);
let order = [];
for (hid in hst) {
for (wid in wrk) {
// ( 0.1%) ""
let widsrc = hst[hid].wid;
let idx = widsrc + '|' + wid + '|' + hst[hid].hst.cpu.toFixed(1);
if (idx in checked) {
continue;
}
let _S = moveCheck(col, hid, wid);
if (_S === undefined) {
_S = currS;
}
checked[idx] = {
hid
, wid
, S : _S
};
order.push(checked[idx]);
}
}
order.sort((x, y) => distS(x.S) - distS(y.S));
return order;
};
let currS = S(col);
let order = moveRanker(col);
let opt = order[0];
console.log('best move', opt);
//
if (distS(opt.S) < distS(currS)) {
console.log('move!', opt.hid, opt.wid);
move(col, opt.hid, opt.wid);
console.log('after move', JSON.parse(JSON.stringify(col)));
return true;
}
else {
console.log('none!');
}
return false;
};
// -
while(iterReOrder(col));En conséquence, la charge sur nos réservoirs est répartie presque de la même manière à chaque instant, nivelant rapidement les pics émergents: