Courbes de Bézier
La logique derrière la construction des courbes de Bézier est bien comprise à partir de l'animation suivante:

Pour obtenir la formule directement à partir de la représentation graphique, il suffit de définir une fonction auxiliaire d'interpolation linéaire entre deux points, à laquelle, lorsque le paramètre t passe de 0 à 1, il renvoie des valeurs intermédiaires de a à b :
Remarque
- lerp, blend, mix - . .
Avec son aide, vous pouvez toujours trouver les points nécessaires - trouvez d'abord
et
et puis à travers eux trouver
Si vous le souhaitez, vous pouvez substituer les fonctions les unes aux autres et réduire - bien que cela ne simplifie pas particulièrement les calculs, cela vous permettra de généraliser les courbes à un nombre arbitraire de points de contrôle (via les polynômes de Bernstein). Dans notre cas, nous obtenons
L'augmentation de l'ordre des courbes est réalisée de manière triviale - les points initiaux ne sont pas fixés constants, mais à la suite d'une interpolation entre n + 1 autres points de contrôle:
Remarque
, . .
Courbes circulaires
Arc de cercle
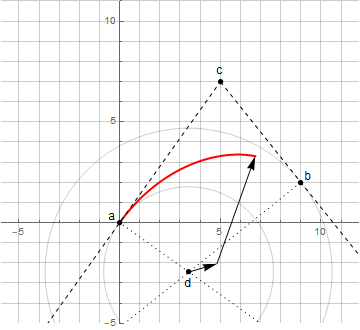
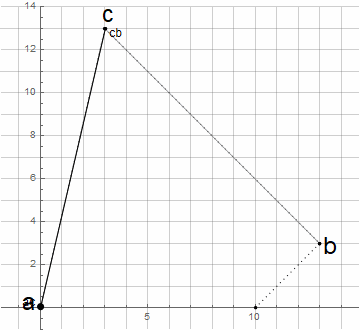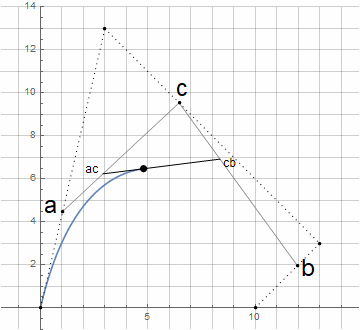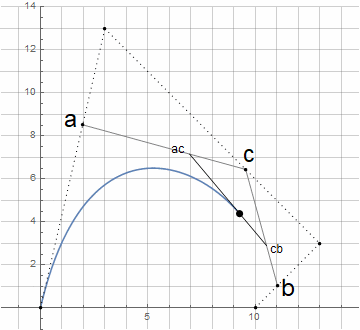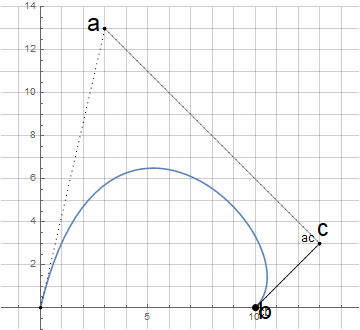
Pour construire un arc de cercle de la même manière, il est nécessaire de déterminer la logique de construction appropriée - par analogie avec le dessin d'un cercle avec une boussole.

Au départ, nous ne connaissons pas le centre du cercle d - il se trouve par l'intersection des perpendiculaires aux tangentes aux points a et b (ci-après nodaux); les tangentes elles-mêmes sont spécifiées au point c (ci-après dénommé la directive). Pour créer un arc de cercle arbitraire (moins de 180 °), il suffit que les distances du point directeur aux points nodaux soient les mêmes.

Arc d'ellipse
Construire un arc d'ellipse est déjà plus difficile - vous avez besoin de deux vecteurs tournant dans des directions différentes ( plus de détails ici )
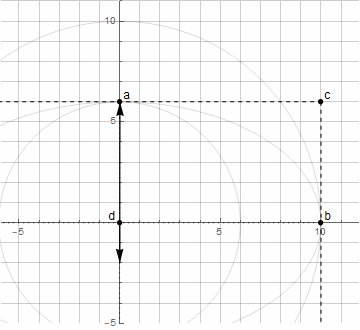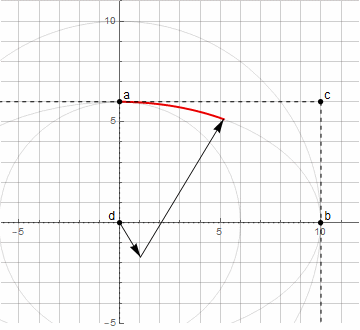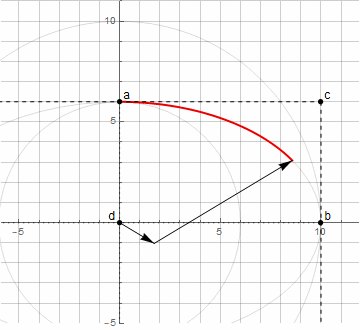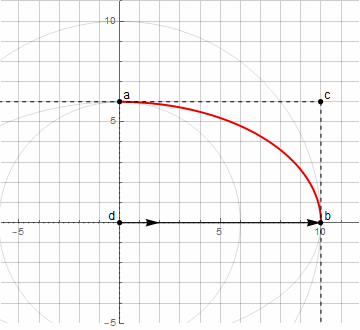
En utilisant la méthode ci-dessus pour trouver le point d , nous ne pouvons plus construire un arc arbitraire d'ellipse - seulement de 0 ° à 90 ° (y compris tourné d'un certain angle).
Arc hypotrochoïde
En posant la condition qu'au début et à la fin du dessin les vecteurs doivent se trouver sur une ligne droite, nous obtenons l'arc de l' hypotrochoïde dans tous les autres cas. Cette condition n'est pas accidentelle et (outre la définition unique de la courbe) garantit la coïncidence des tangentes aux points nodaux. En conséquence, les chemins angulaires parcourus par les deux vecteurs seront différents, mais totalisent toujours 180 °.

L'animation suivante montre comment la forme de la courbe change en fonction de la position du point de repère:

Algorithme
Comme nous avons ici des rotations sur un plan bidimensionnel, il est pratique de décrire les mathématiques de la construction de ces courbes en termes de nombres complexes.
1) trouver le point d'intersection des normales des tangentes tracées du point directeur aux points nodaux:
(ici l'astérisque signifie conjugaison complexe).
2) connaissant d , on trouve les longueurs des normales
et leur somme et différence
3) trouver le vecteur unitaire à partir duquel la construction commence
Remarque
sign(x).
4) trouver les chemins angulaires que chacun des vecteurs doit passer
Remarque
, — . — , . . .
, — , - ; .
. ,
— - .
, — , - ; .
. ,
— - .
5) en changeant successivement t de 0 à 1 avec un certain pas, on trouve le point appartenant à la courbe par la formule
Splines circulaires
Tout comme les courbes de Bézier, ces courbes peuvent être combinées pour créer des splines continues par morceaux. Pour garantir la fluidité des points d'ancrage (ancrage), le point d'ancrage doit être aligné avec deux points directeurs adjacents. Pour ce faire, vous pouvez spécifier des points d'ancrage non explicitement, mais via l'interpolation des points directeurs. Ils ne peuvent pas non plus être réglés du tout, calculant de manière complètement automatique - par exemple, comme la moyenne entre les points de guidage: à

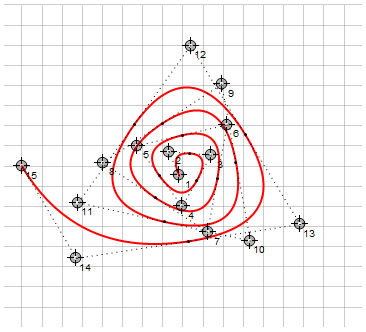
droite, à des fins de comparaison, la même approche a été utilisée avec les courbes de Bézier du 2ème ordre.
Notes et nuances
Contrairement aux courbes de Bézier, ici la courbe ne se situe pas toujours dans la forme des lignes reliant les points de contrôle, par exemple
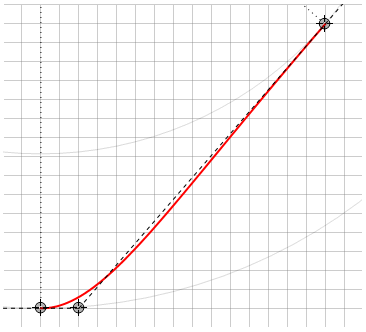
De plus, il existe un cas dégénéré qui doit être traité séparément - lorsque le point directeur se trouve sur la même ligne que les points d'ancrage. Dans ce cas, la courbe dégénère en une ligne droite et lors de la tentative de calcul du point d , une division par zéro se produit.
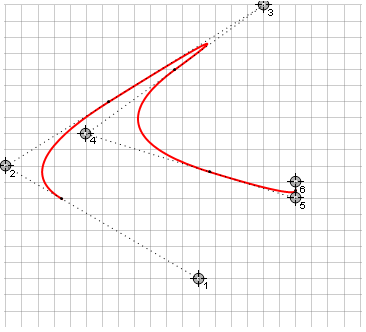
Ces courbes ont également des restrictions sur la courbure de la ligne, car l'algorithme choisit le plus petit chemin à suivre et la courbe ne peut pas faire plus de 180 °. Cela conduit au fait qu'avec une interpolation continue par morceaux, des angles vifs peuvent se produire à une certaine position des points directeurs (à droite - les mêmes points pour Bézier):
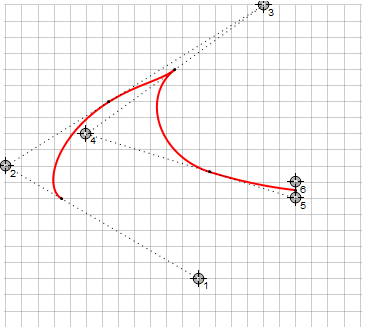
Conclusion
Le développement ultérieur de la méthode considérée de construction de courbes est une augmentation du nombre de vecteurs impliqués dans la construction de la courbe et, par conséquent, une augmentation du nombre de points directeurs. Cependant, contrairement aux courbes de Bézier, l'augmentation de l'ordre n'est pas évidente ici et nécessite une réflexion réfléchie séparée. Diverses méthodes pour les combiner avec les courbes de Bézier sont également possibles - en particulier, l'interpolation du centre du cercle des vecteurs de dessin.
La méthode envisagée de construction de courbes n'est pas non plus la seule, dont un cas particulier sont des arcs de cercle et une ellipse - au moins, une ellipse peut être construite à travers l' intersection de lignes droites dans un parallélogramme(cependant, dans cette version, l'auteur a échoué). Il est possible qu'il existe d'autres solutions, y compris des options décrites dans l'article - écrivez dans les commentaires si vous savez quelque chose sur ce sujet.
Le code source de l'article peut être téléchargé à partir de GitHub .