Vos carrés sont faux

L'autre jour, il y avait un article consacré à la différence entre un carré aux bords arrondis et un «cercle carré» - une figure intermédiaire entre un cercle et un carré, obtenue à partir de la formule de la superellipse . Les opinions des lecteurs étaient partagées - tout le monde n'a pas vu la différence, et qui a vu - tout le monde n'a pas préféré l'option «correcte». Et je soupçonne pourquoi: vos carrés ne sont pas réels!

Solution alternative

Ma solution (en coordonnées polaires) s'est avérée comme ceci:

$$

$$\rho =\sqrt{\frac{2}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin ^2(2 \phi )}}}$$

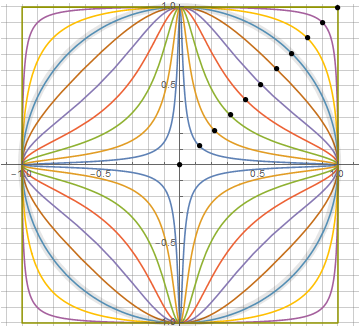
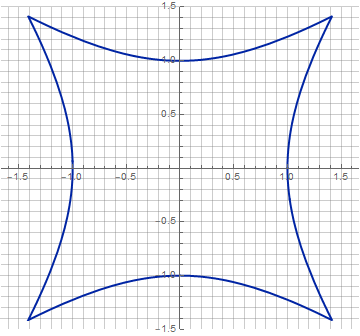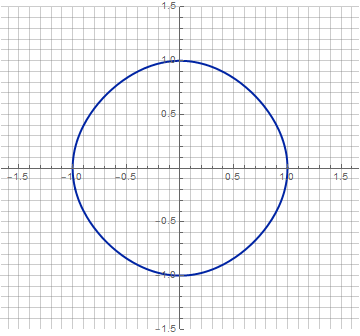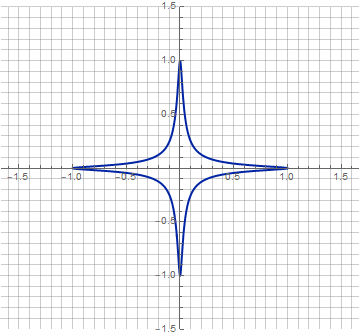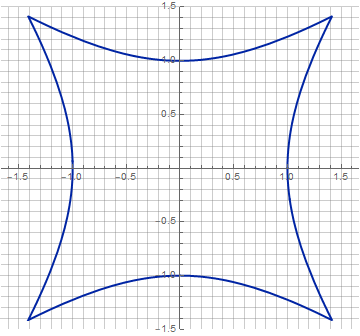
dans quel paramètre $$$k$de 0 à 1 définit le degré de "quadrature", et linéairement - définissant le point d'intersection ( k , k ) de la figure avec la diagonale. Cela signifie que nous pouvons définir de manière unique notre cercle carré à travers 3 points. Et oui, avec$$$k = 1$nous avons un vrai carré, avec des côtés droits et des angles vifs. Eh bien, le cercle, respectivement, est obtenu lorsque$$$k = \frac{1}{\sqrt{2}}$(cosinus 45 °). Les variantes des chiffres résultants sont reflétées sur le KDPV.



Vous pouvez également noter que cette formule ne contient pas d'astuces telles que les fonctions de module, les fonctions de signe / rejet, etc. - comme cela est requis pour une superellipse. Tout est juste, seulement des fonctions mathématiques standard, avec lesquelles il n'y aura aucune difficulté à différencier ou à intégrer. À propos de l'intégration - si vous le souhaitez, vous pouvez également trouver la zone de ces figures (via des intégrales elliptiques):

$$

$$\frac{4 k^4 E\left(\frac{2 k^2-1}{k^4}\right)-4 \left(k^2-1\right)^2 K\left(\frac{2 k^2-1}{k^4}\right)}{2 k^2-1}$$

Développement

Vous pouvez ajouter plus de variation aux formes résultantes. Par exemple, comme ceci:

$$

$$\rho =\sqrt{\frac{1+\sqrt{\frac{(z-2)^2}{z^2}}}{1+\sqrt{1+\left(\frac{1}{k^4}-\frac{2}{k^2}\right) \sin^2(2\phi)+\left(\frac{4(1-z)}{z^2}\right)\cos^2(2 \phi)}}}$$

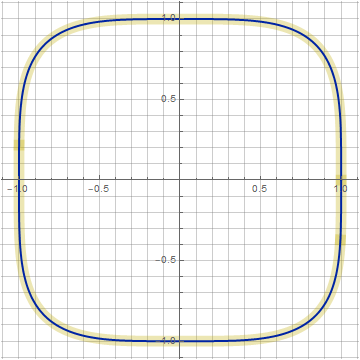
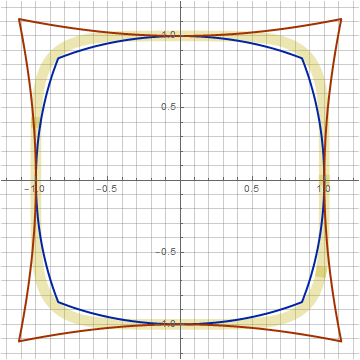
Ici, nous avons encore un paramètre z , qui nous permet de déformer la figure sans violer l'idéologie de la construction. Avec son aide, vous pouvez rapprocher notre figure de la superellipse (représentée en jaune sur les graphiques). Par exemple, pour n = 4 ( k = 0,266, z = 0,1), la correspondance est presque parfaite:







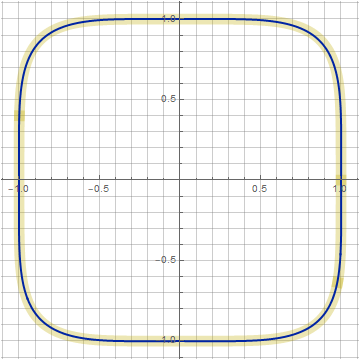
à n supérieur , la différence est déjà plus sensible ( n = 5, k = 0,6, z = 0,48):







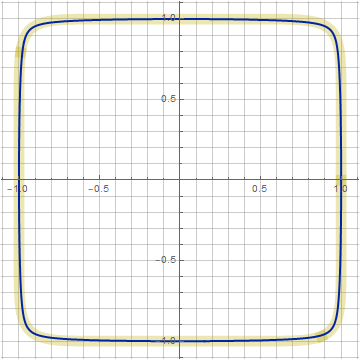
n = 10, k = 0,942, z = 1,02:





Et oui, vous pouvez y aller de manière complètement radicale! Cette conception d'icône ne peut certainement pas être confondue avec quoi que ce soit:







Eh bien, vous pouvez aussi rêver un peu avec de l'animation:

Conclusion

Si un concepteur d'une certaine entreprise avec (éventuellement) un logo de fruits veut obtenir un design unique, même s'il ne diffère pas fondamentalement des solutions existantes, il peut être utile d'essayer de rechercher et de breveter une formule vraiment nouvelle, et de ne pas attirer une solution connue depuis longtemps en y accrochant des tonnes de bulletins marketing. ... Surtout si cela peut être fait juste pour le plaisir par une simple personne de province sans éducation spéciale.



Les codes source PS de l'article sont ici .



PPS Grâce à l'équation de la courbe en coordonnées cartésiennes, la formule originale ressemblera à

$$

$$0=-2+\left(x^2+y^2\right) \left(1+\sqrt{1+\frac{\left(4-8 k^2\right) x^2 y^2}{k^4 \left(x^2+y^2\right)^2}}\right)$$