Certains attracteurs envoûtent par leur beauté même dans les images statiques. Nous voulions faire une application capable de visualiser la plupart des attracteurs en dynamique, en 3D et sans décalage.
À propos de nous
Nous sommes Roman Venediktov, Vladislav Nosivskoy et Kirill Karnaukhov - étudiants de deuxième année du programme de licence "Mathématiques appliquées et informatique" à l'École supérieure d'économie de Saint-Pétersbourg. Nous aimons la programmation depuis l'école. Tous les trois étaient engagés dans la programmation des Olympiades et sont passés différentes années à l'étape finale de l'Olympiade panrusse des écoliers en informatique, mais ils n'avaient aucune expérience en programmation industrielle auparavant, et pour nous, c'est le premier grand projet d'équipe. Nous l'avons défendu comme un article sur le C ++.
La modélisation
Il existe de nombreuses façons de définir un système dynamique avec un attracteur étrange, mais la plus courante est un système de trois équations différentielles du premier ordre. Nous avons commencé avec elle.
Avant de visualiser quelque chose, vous devez simuler le processus lui-même et trouver les trajectoires des points. Les méthodes de modélisation précises sont assez laborieuses, et nous aimerions le faire le plus rapidement possible.
Lors de l'implémentation de la modélisation, nous avons décidé d'utiliser la métaprogrammation, abandonnant std :: function et d'autres mécanismes similaires. Ils auraient pu simplifier l'architecture et le codage, mais ils auraient considérablement réduit les performances, ce que nous ne voulions pas.
Au départ, la méthode Runge - Kutta la plus simple du 4ème ordre de précision avec un pas constant a été utilisée pour la modélisation. Jusqu'à présent, nous ne sommes pas retournés à l'augmentation du nombre de méthodes et d'autres composants mathématiques du modèle, et maintenant c'est la seule méthode présentée. Sur la plupart des systèmes trouvés, il est suffisamment précis pour produire des images similaires à des images provenant d'autres sources.
Le modèle accepte en entrée:
- le foncteur «dérivés» pour obtenir des dérivées par les coordonnées d'un point;
- le foncteur «observateur», qui est appelé à partir du point dès qu'il est reçu;
- paramètres de simulation (point de départ, taille du pas, nombre de points).
À l'avenir, vous pourrez ajouter une vérification pour voir comment l'image présentée correspond à la vraie, des méthodes de modélisation plus solides (par exemple, en connectant la bibliothèque Boost.Numeric.Odeint) et d'autres méthodes d'analyse pour lesquelles nos connaissances en mathématiques ne sont toujours pas suffisantes.
Systèmes
Nous avons trouvé les systèmes attracteurs étranges les plus populaires pour en tirer les meilleures performances. Ici, nous voulons dire merci au site chaoticatmospheres.com, qui a rendu cette recherche très facile pour nous.
Tous les systèmes ont dû être enveloppés pour que, malgré le fait qu'ils soient tous "nos modèles", ils puissent être placés dans un conteneur et fonctionner normalement avec eux dans le contrôleur. Nous sommes arrivés à la solution suivante:
- DynamicSystem ‘observer’, (, ...) std::function ‘compute’. ‘Compute’ , , ‘derivatives’ .
- std::function , DynamicSystemInternal compute .
- DynamicSystemInternal ‘observer’, ‘derivatives’. ‘derivatives’, .
Nous avons commencé à travailler sur l'ajout d'un DynamicSystemWrapper, qui posséderait le DynamicSystem et pourrait effectuer le prétraitement nécessaire à la visualisation (sélection d'une constante pour la normalisation, erreur acceptable pour les méthodes avec contrôle de longueur d'étape ...), mais n'avons pas eu le temps de terminer.
Visualisation
Nous avons choisi OpenGL comme bibliothèque de rendu en raison de ses performances et capacités, ainsi que Qt5, qui a un wrapper pratique sur OpenGL.
Pour commencer, nous voulions apprendre à dessiner au moins quelque chose, et après un certain temps, nous avons pu créer notre premier cube. Peu de temps après, une version simple du modèle mathématique est apparue, et voici la première visualisation de l'attracteur:
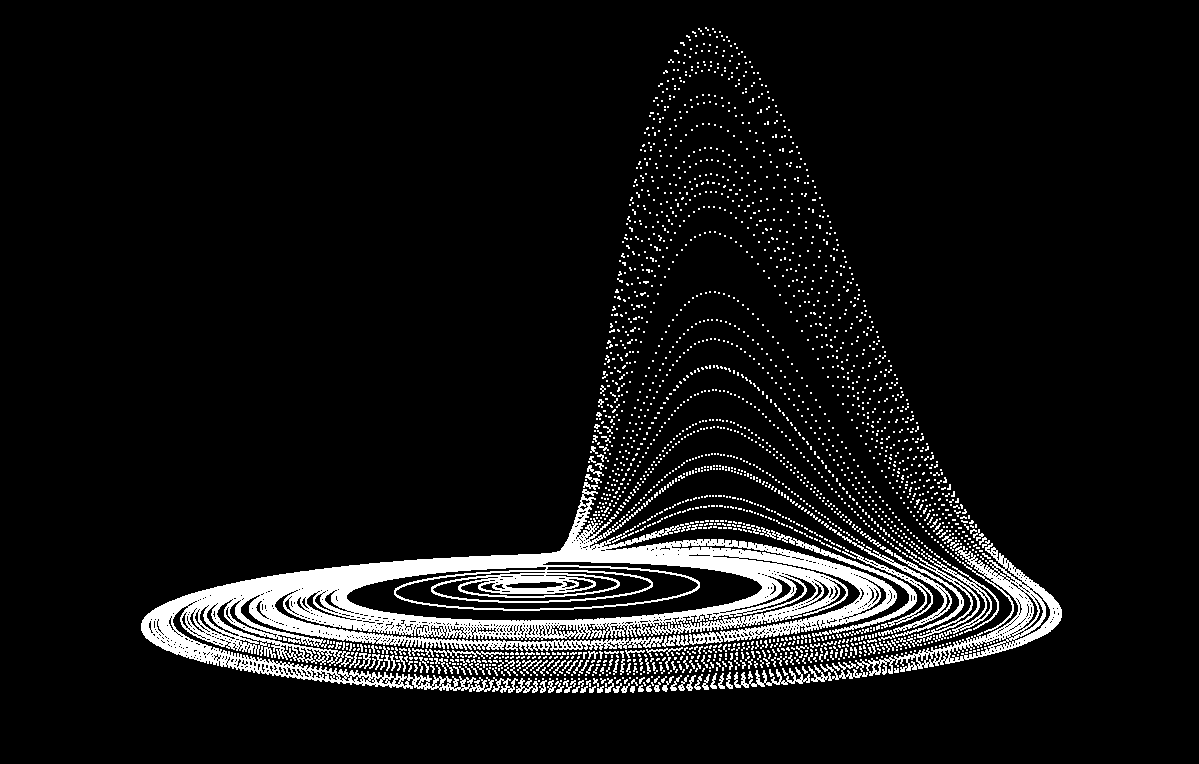
Avec la première version du rendu, une version très simple de la caméra était également prête. Elle savait tourner autour d'un point et s'approcher / s'éloigner. Nous voulions plus de liberté dans l'espace: les attracteurs sont différents et doivent être explorés de différentes manières. Puis une deuxième version de la caméra est apparue, qui pouvait tourner et se déplacer librement dans toutes les directions (nous étions guidés par la caméra dans Minecraft). À cette époque, l'algèbre linéaire ne faisait que commencer, et donc il n'y avait pas assez de connaissances: nous devions chercher beaucoup d'informations sur Internet.
Pendant tout ce temps, les images étaient blanches, statiques et sans intérêt. Je voulais ajouter des couleurs et de la dynamique. Pour commencer, nous avons appris à peindre l'ensemble du tableau en une seule couleur, mais cela s'est également révélé inintéressant. Ensuite, nous avons proposé la solution suivante:
- Prenez beaucoup (100-500, vous pouvez en choisir plus dans les paramètres, l'essentiel est que les performances soient suffisantes) proches les uns des autres points de départ.
- Simulez la trajectoire de chacun d'eux.
- Effectuez le rendu des tracés en même temps, tout en les colorant de différentes couleurs, et n'affichez que le segment du tracé.
Il s'est avéré ce qui suit:

Environ un tel schéma est resté jusqu'à la fin.
Nous avons été frappés par le fait que les lignes sont trop "anguleuses" et nous avons décidé d'apprendre à les lisser. Bien sûr, nous avons essayé de réduire l'étape de simulation, mais, malheureusement, même les processeurs modernes ne sont pas capables de compter un tel nombre de points. Il fallait chercher une autre option.
Au début, nous pensions qu'OpenGL devait avoir un outil d'anti-aliasing, mais après de nombreuses recherches, nous avons constaté que ce n'était pas le cas. Puis l'idée est venue d'interpoler les courbes et d'en ajouter un peu plus entre chaque paire de points voisins suffisamment éloignés. Pour ce faire, il était nécessaire de choisir une méthode d'interpolation des courbes, et il existe de nombreuses méthodes de ce type. Hélas, la plupart d'entre eux (par exemple, la courbe de Bézier) nécessitaient quelques points supplémentaires à préciser, ce qui n'était clairement pas adapté à notre tâche: nous voulions que le résultat ne dépende que de ce que le modèle mathématique nous a donné. Au bout d'un moment, nous avons trouvé une interpolation appropriée: la courbe Catmull - Roma. Il s'est avéré comme ceci:

Après cela, nous avons décidé que ce serait bien d'enregistrer des vidéos dans l'application. Nous voulions le garder multi-plateforme, nous avons donc opté pour la bibliothèque libav (il n'y avait presque pas de choix parmi les bibliothèques). Malheureusement, toute la bibliothèque est écrite en C et possède une interface très peu pratique, il nous a donc fallu beaucoup de temps pour apprendre à écrire quelque chose. Tous les gifs suivants sont créés à l'aide de l'enregistrement intégré.

Jusqu'à ce point, toutes les couleurs de courbe ont été explicitement spécifiées lors de la création. Nous avons décidé que pour une belle image, nous devons définir les couleurs différemment. Pour ce faire, seules les couleurs témoins ont commencé à être indiquées, et le reste a été calculé à l'aide d'un dégradé linéaire. Cette partie a été transférée aux shaders (avant cela, ils étaient standard).
Nous avons trouvé intéressant de colorer les trajectoires de telle sorte que chacune d'elles change de couleur de la tête à la queue. Cela nous permet d'observer l'effet de la vitesse:
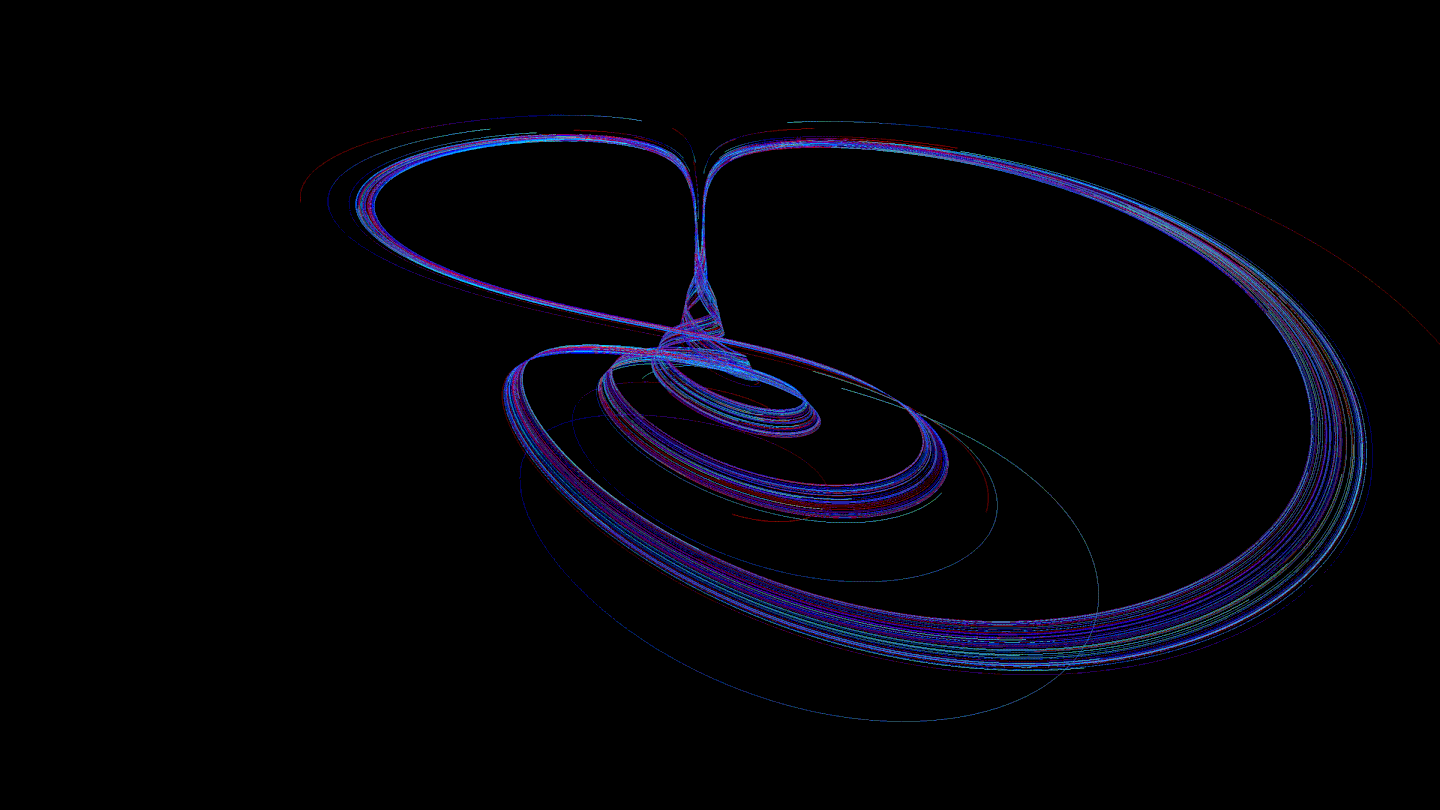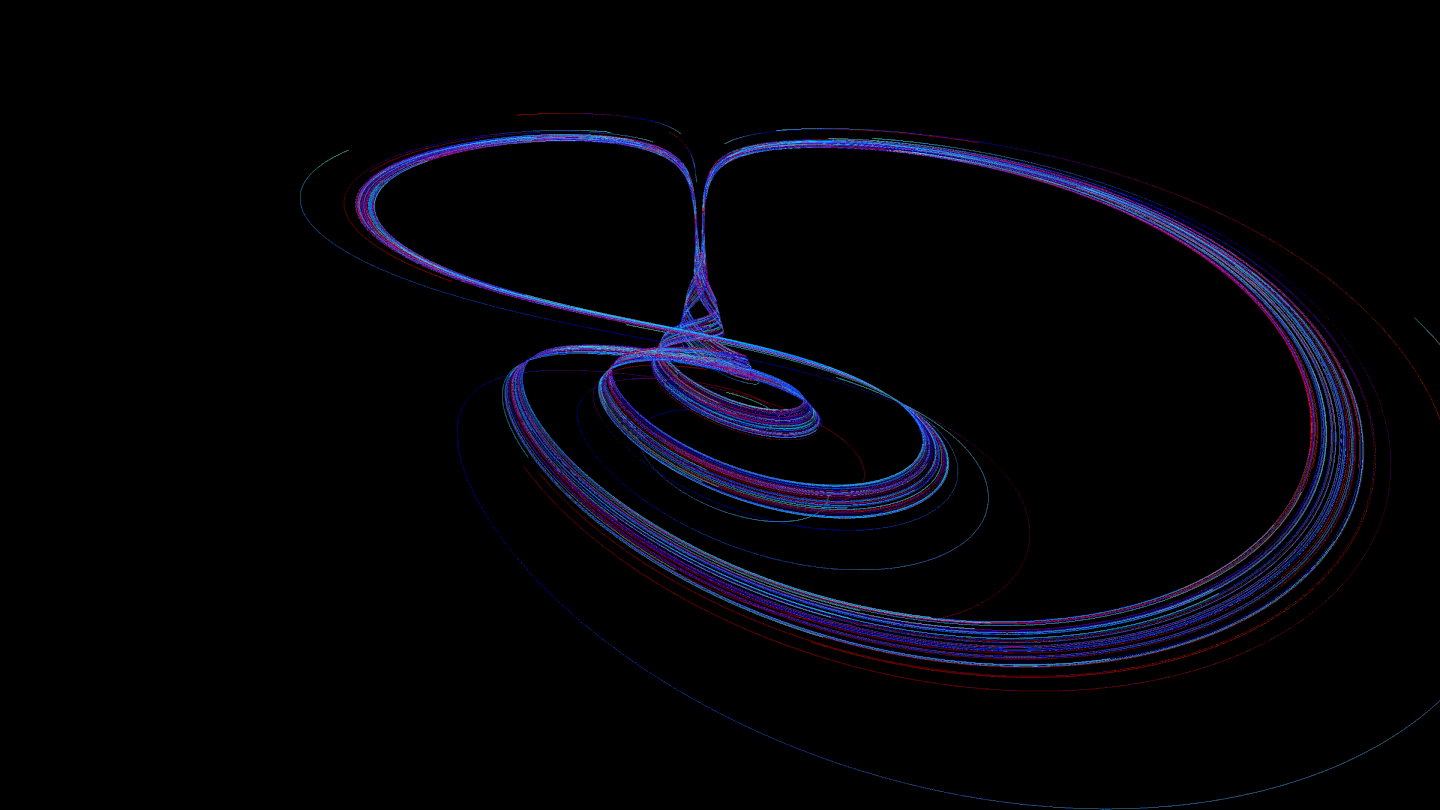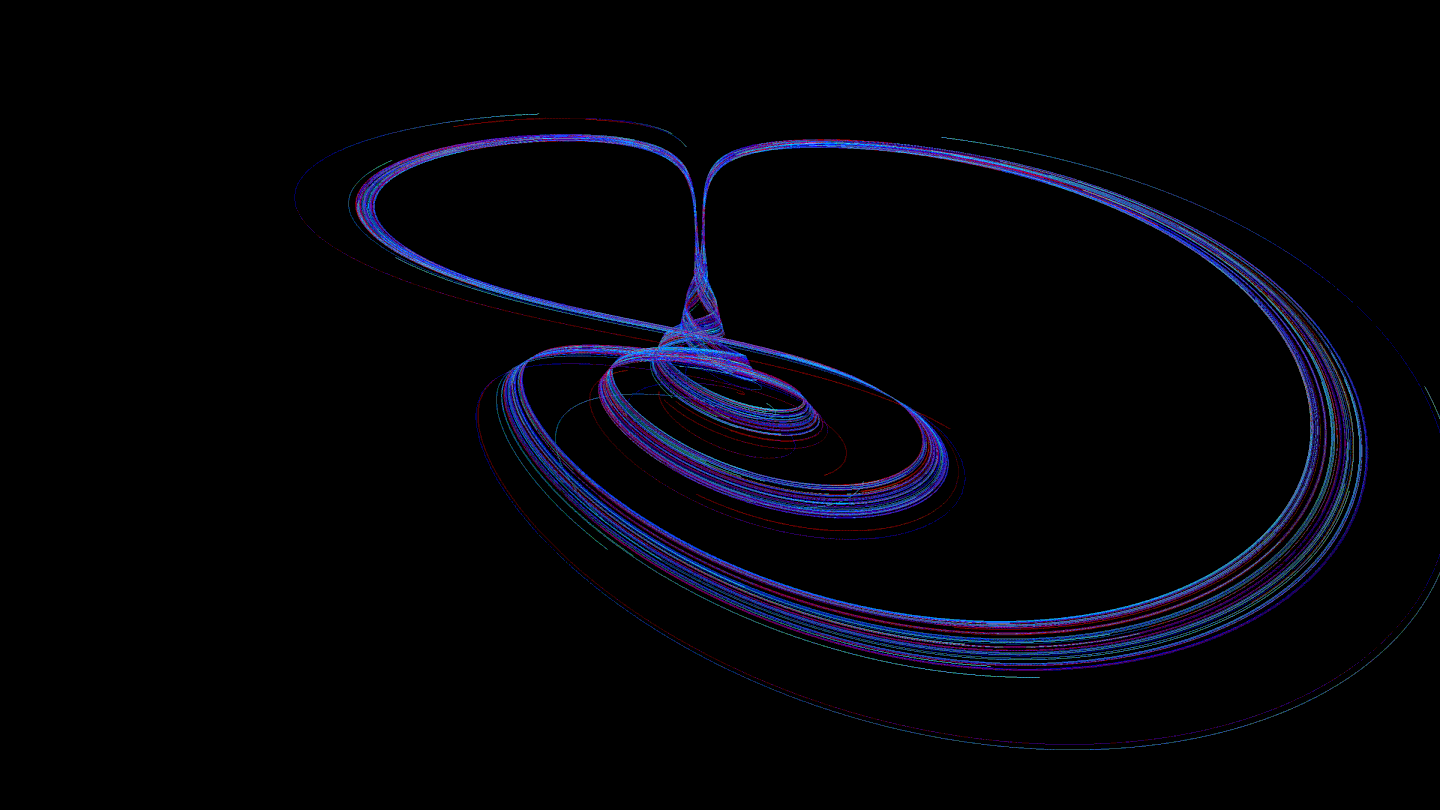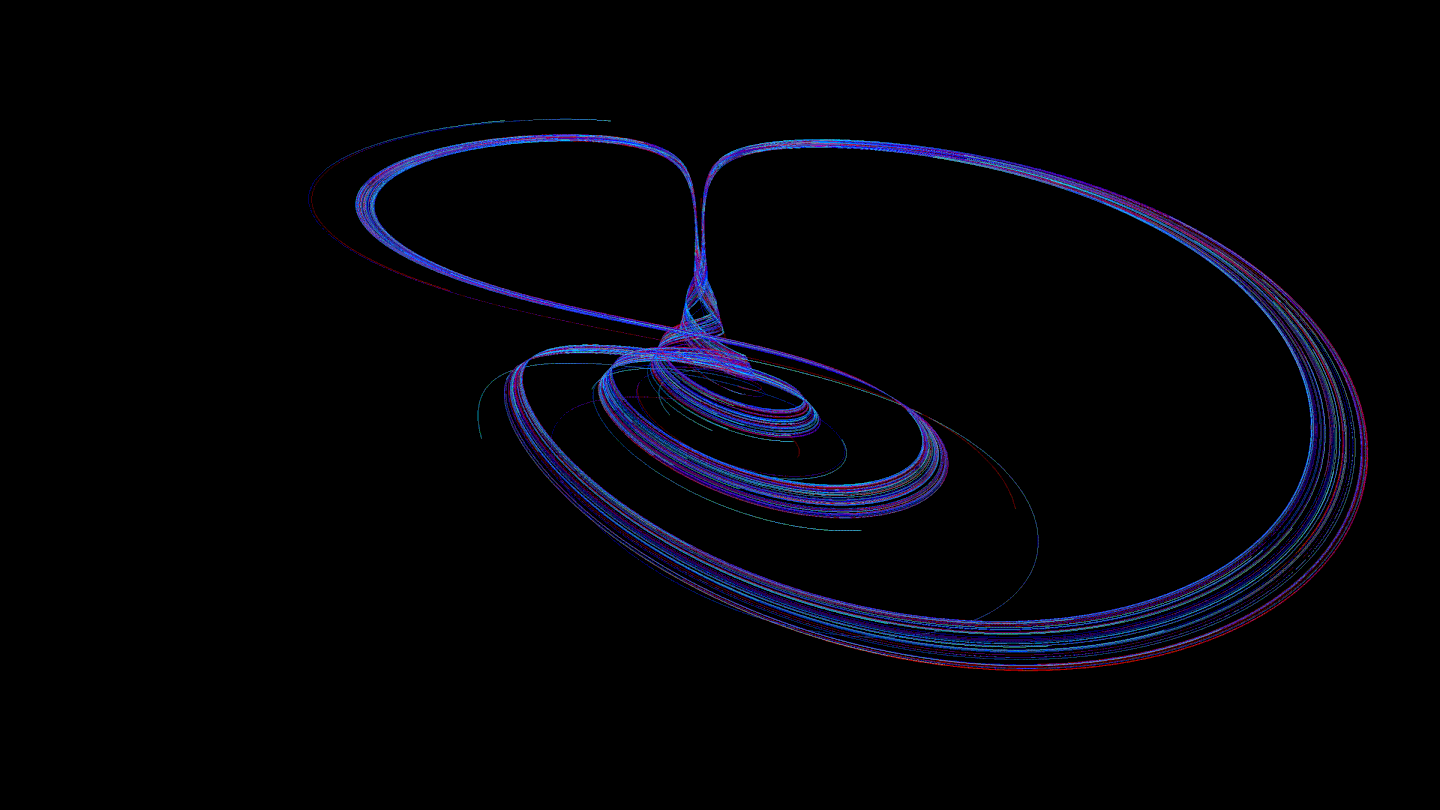
Ensuite, nous avons pensé qu'il valait la peine d'essayer de réduire le temps de prétraitement de la trajectoire: l'interpolation d'une courbe est une opération "coûteuse". Il a été décidé de transférer cette partie vers des shaders afin que le GPU calcule l'interpolation à chaque fois qu'on lui demande de dessiner une partie de la trajectoire. Pour cela, nous avons utilisé le Geometry Shader. Cette solution présentait de nombreux avantages: pas de retard du côté du rendu avant le rendu, la possibilité de lisser encore plus les courbes (ces calculs sont effectués sur le GPU plus rapidement que sur le CPU), l'utilisation de moins de RAM (avant cela, tous les points interpolés devaient être stockés, maintenant - non ).
Contrôleur et interface utilisateur
Après avoir choisi Qt5 comme framework de base, la question du choix des technologies pour l'interface a immédiatement disparu. Le Qt Creator intégré satisfait suffisamment tous les besoins d'une petite application.
Pour répondre aux demandes des utilisateurs, un contrôleur devait être écrit. Heureusement, Qt dispose de moyens pratiques pour gérer les frappes et saisir des valeurs dans les champs. Il utilise l'idée principale de Qt - le mécanisme de signal et de slot. Par exemple, si dans notre application nous appuyons sur le bouton responsable de la reconstruction du modèle, un signal sera généré qui sera accepté par le slot du gestionnaire. Il lancera la reconstruction elle-même.
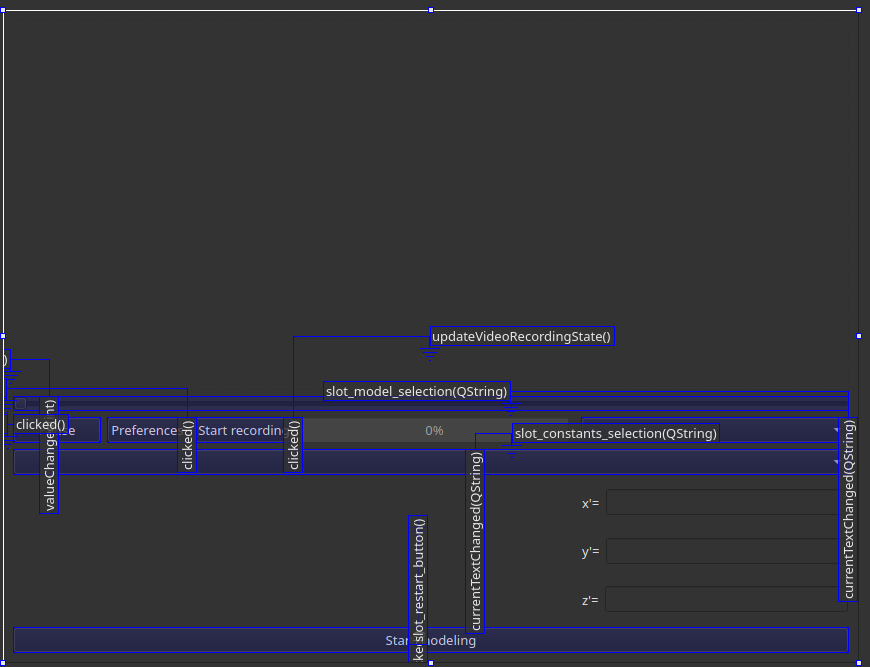
Lors du développement de presque toutes les applications avec une interface, l'idée de rendre l'application multithread apparaît tôt ou tard. Cela nous a semblé nécessaire: la construction de modèles intégrés a pris plusieurs secondes, et la construction d'un modèle personnalisé a pris 10 secondes. En même temps, bien sûr, l'interface s'est bloquée, car tous les calculs étaient effectués dans un seul thread. Pendant assez longtemps, nous avons discuté de différentes options et pensé à l'asynchronie en utilisant std :: async, mais à la fin nous avons réalisé que nous voulions pouvoir interrompre les calculs dans un autre thread. Pour ce faire, j'ai dû écrire un wrapper sur std :: thread. Tout est aussi simple que possible: un drapeau atomique pour la vérification et une interruption nette si la vérification échoue.
Cela a donné non seulement le résultat souhaité - l'interface a cessé de se bloquer - mais a également ajouté une fonctionnalité: en raison des particularités de l'architecture et de l'interaction entre les données du modèle et la visualisation, il est devenu possible de tout dessiner en ligne, au cours du comptage. Auparavant, vous deviez attendre toutes les données.
Systèmes personnalisés
Il existe de nombreux attracteurs déjà fournis dans l'application, mais nous voulions également permettre à l'utilisateur de saisir les équations lui-même. Pour cela, nous avons écrit un analyseur qui supporte les variables (x, y, z), les opérations mathématiques standards (+ - * / ^), les constantes, de nombreuses fonctions mathématiques (sin, cos, log, atan, sinh, exp, etc.) et crochets. Voilà comment cela fonctionne:
- La chaîne de requête d'origine est tokenisée. Ensuite, les jetons sont analysés de gauche à droite et un arbre d'expression est construit.
- Les opérations possibles sont divisées en groupes. Chaque groupe a son propre Node. Groupes: plus-moins, multiplication-division, exponentiation, moins unaire, soi-disant feuilles (cela inclut les constantes, les variables, les appels de fonction).
- Chaque groupe a son propre niveau de calcul. Chaque niveau entraîne des calculs récursifs aux niveaux suivants. Vous pouvez voir que l'ordre des appels affecte la distribution des priorités des opérations. Nous les avons dans l'ordre décrit ci-dessus.
Recherchez plus de détails dans le code source de l'analyseur .
Chaque niveau renvoie une sorte d'héritier du nœud. Il y en a quatre:
- opérateur binaire - stocke des pointeurs vers deux enfants et son propre type d'opération;
- opérateur unaire - stocke un pointeur vers l'enfant et son propre type d'opération. Cela inclut les fonctions, car il s'agit d'un cas particulier d'opération unaire;
- constant - stocke sa valeur;
- variable - stocke un pointeur vers l'endroit en mémoire où se trouve sa valeur.
La structure Node a uniquement une fonction de calcul virtuelle qui renvoie la valeur de son sous-arbre.
La sortie résultante est très bien adaptée à l'architecture système décrite précédemment. Un lambda est simplement passé à DynamicSystemInternal, qui stocke des pointeurs vers les nœuds racine des trois arbres obtenus et les positions de mémoire xyz des valeurs. Lorsqu'il est appelé, il remplace les valeurs fournies par celles fournies et appelle calc à partir des sommets racine.
Résultat
En conséquence, nous avons un programme qui peut visualiser les systèmes définis par l'utilisateur et qui dispose d'une base d'un grand nombre d'attracteurs. Elle le fait très bien et optimisé, ce qui est une bonne nouvelle.
Mais il y a encore beaucoup de travail:
- ajouter des méthodes plus précises;
- ajouter une couche supplémentaire de traitement des systèmes (normalisation et sélection automatique des erreurs dans des méthodes plus complexes);
- améliorer le travail avec les systèmes utilisateurs (prise en charge des variables, sauvegarde);
- optimiser leur travail (compilation JIT ou un utilitaire qui convertit les systèmes enregistrés en code c ++ et démarre simplement la recompilation pour qu'ils atteignent les performances des systèmes embarqués);
- ajouter des capacités d'analyse ou de visualisation des résultats dont les personnes qui travaillent avec de tels systèmes ont vraiment besoin;
- ...
Notre référentiel .
Et quelques autres vidéos avec des attracteurs: