
Les dernières années d'apprentissage en profondeur ont été une série continue de réalisations: de la défaite des gens dans le jeu de Go au leadership mondial dans la reconnaissance d'image, la reconnaissance vocale, la traduction de texte et d'autres tâches. Mais ces progrès s'accompagnent d'une augmentation insatiable de l'appétit pour la puissance de calcul. Un groupe de scientifiques du MIT, de l'Université de Yongse (Corée) et de l'Université de Brasilia a publié une méta-analyse de 1058 articles scientifiques sur l'apprentissage automatique . Cela montre clairement que les progrès de l'apprentissage automatique (ML) sont un dérivé de la puissance de calcul du système . Les performances informatiques ont toujours limité les fonctionnalités du ML, mais maintenant les besoins des nouveaux modèles de ML augmentent beaucoup plus rapidement que les performances des ordinateurs.
L'étude démontre que les progrès de l'apprentissage automatique ne sont, en fait, guère plus qu'une conséquence de la loi de Moore. Et pour cette raison, de nombreux problèmes de ML ne seront jamais résolus en raison des limitations physiques de l'ordinateur.
Les chercheurs ont analysé des articles scientifiques sur la classification d'images (ImageNet), la reconnaissance d'objets (MS COCO), les réponses aux questions (SQuAD 1.1), la reconnaissance d'entités nommées (COLLN 2003) et la traduction automatique (WMT 2014 En-to-Fr).

Requêtes de calcul ML, échelle logarithmique Il
a été démontré que les progrès dans les cinq domaines dépendent fortement d'une puissance de calcul accrue. L'extrapolation de cette relation montre clairement que les progrès dans ces domaines deviennent rapidement insoutenables sur les plans économique, technique et environnemental. Ainsi, de nouveaux progrès dans ces applications nécessiteront des méthodes beaucoup plus efficaces en termes de calcul.
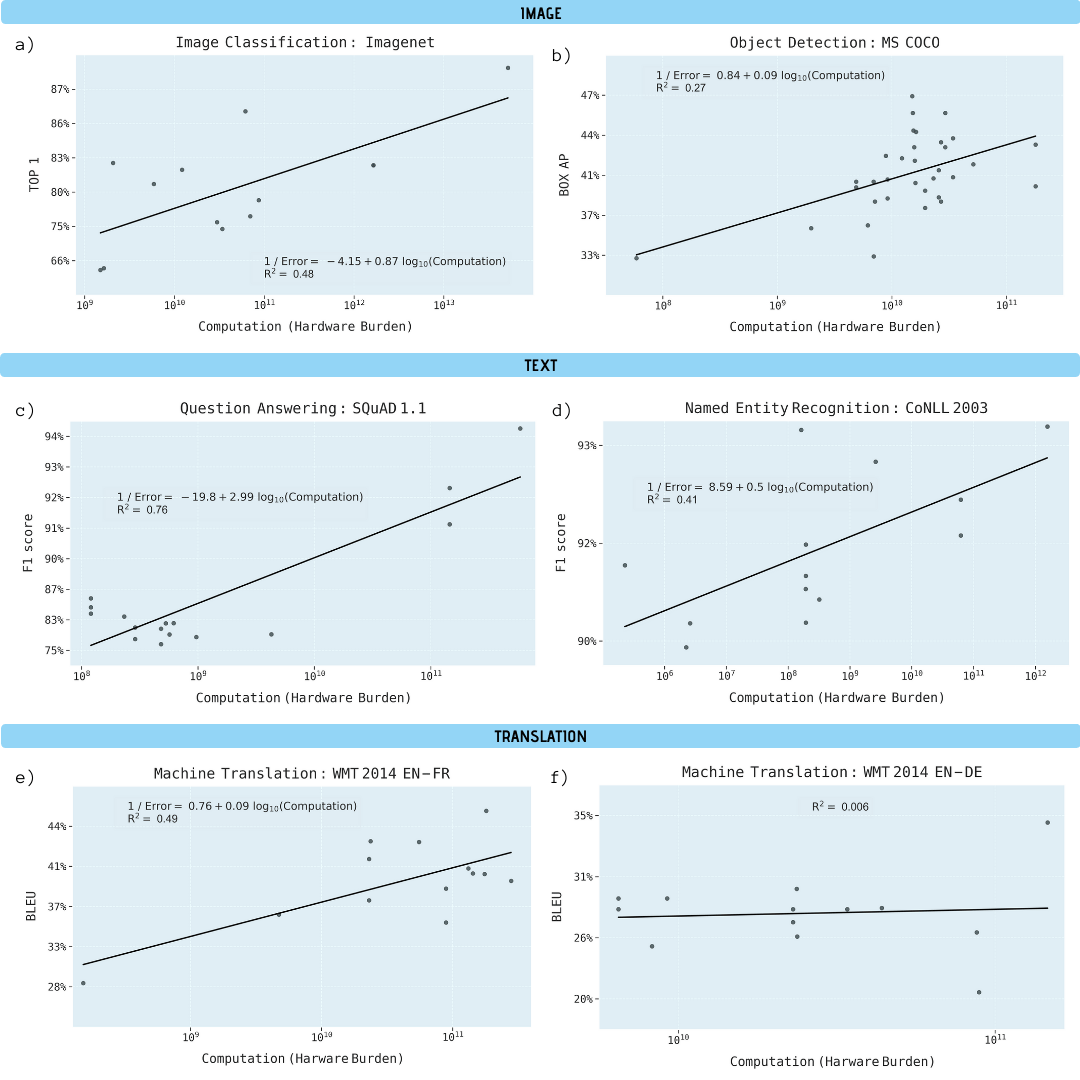
Amélioration des performances dans diverses tâches d'apprentissage automatique en fonction de la puissance de calcul du modèle d'apprentissage (en gigaflops)
Pourquoi l'apprentissage automatique est-il si dépendant de la puissance de calcul?
Il y a des raisons importantes de croire que l'apprentissage en profondeur est intrinsèquement plus dépendant du calcul que les autres méthodes. En particulier, en raison du rôle de l'hyperparamétrisation et de la mise à l'échelle du système, lorsque des données d'apprentissage supplémentaires sont utilisées pour améliorer la qualité du résultat (par exemple, pour réduire le taux d'erreurs de classification, l'erreur quadratique moyenne de régression, etc.).
Il a été prouvé que l'hyperparamétrisation offre des avantages significatifs, c'est-à-dire la mise en œuvre de réseaux de neurones avec plus de paramètres que le nombre de points de données disponibles pour l'entraîner. Classiquement, cela conduirait à un surajustement. Mais les techniques d'optimisation de gradient stochastique fournissent un effet de régularisation au détriment d'un arrêt précoce, mettant les réseaux de neurones en mode d'interpolation où les données d'apprentissage s'adaptent presque exactement, tout en conservant des prédictions raisonnables aux points intermédiaires. Un exemple de réseaux à grande échelle avec hyperparamétrisation est l'un des meilleurs systèmes de reconnaissance de formes NoisyStudent , qui dispose de 480 millions de paramètres pour 1,2 million de points de données ImageNet.
Le problème avec l'hyperparamétrisation est que le nombre de paramètres d'apprentissage profond doit augmenter à mesure que le nombre de points de données augmente. Étant donné que le coût de la formation d'un modèle d'apprentissage en profondeur évolue avec le produit du nombre de paramètres et du nombre de points de données, cela signifie que l'exigence de calcul augmente d'au moins le carré du nombre de points de données dans un système hyperparamétrisé. La mise à l'échelle quadratique n'évalue pas encore suffisamment la vitesse de croissance des réseaux d'apprentissage profond, car la quantité de données d'entraînement doit évoluer beaucoup plus rapidement que linéairement pour obtenir des améliorations linéaires des performances.
Considérons un modèle génératif qui a 10 valeurs non nulles sur 1000 possibles, et considérons quatre modèles pour essayer de découvrir ces paramètres:
- : 10
- : 9 1
- : 1000 ,
- : , 1000 , ()
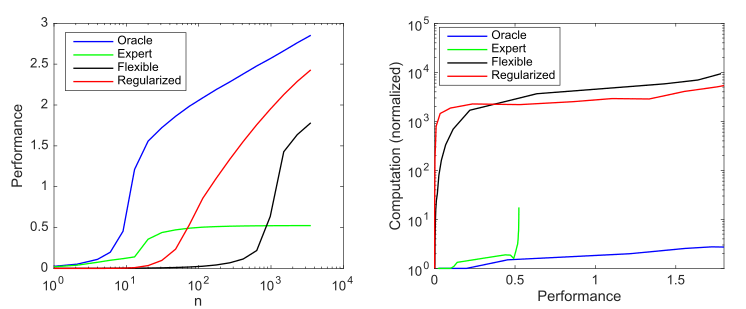
Impact de la complexité et de la régularisation du modèle sur les performances du modèle (mesuré comme erreur quadratique moyenne normalisée log 10 négative par rapport au prédicteur optimal) et sur les besoins de calcul en moyenne sur 1000 simulations par cas; a) productivité moyenne à mesure que la taille des échantillons augmente; b) Calcul moyen requis pour améliorer les performances
Ce graphique résume le principe décrit par Andrew Ng: Les méthodes traditionnelles d'apprentissage automatique fonctionnent mieux sur les petites données, mais les modèles de ML flexibles fonctionnent mieux sur les mégadonnées. Un phénomène courant des modèles agiles est qu'ils ont un potentiel plus élevé, mais aussi beaucoup plus de données et de besoins en calcul.
Nous pouvons voir que l'apprentissage en profondeur fonctionne bien car il utilise l'hyperparamétrisation pour créer un modèle très flexible et une régularisation (implicite) pour réduire la complexité de l'échantillon à un niveau acceptable. Dans le même temps, cependant, l'apprentissage en profondeur nécessite beaucoup plus de calculs que les modèles plus efficaces. Ainsi, augmenter la flexibilité du ML implique une dépendance à de grandes quantités de données et de calcul.
Limites de calcul
Les performances informatiques ont toujours limité la puissance des systèmes ML.
Par exemple, Frank Rosenblatt a décrit le premier réseau neuronal à trois couches en 1960. On espérait qu'elle "démontrerait les possibilités d'utiliser le perceptron comme dispositif de reconnaissance de formes". Mais Rosenblatt a constaté que «à mesure que le nombre de connexions sur le réseau augmente, la charge sur un ordinateur numérique typique devient rapidement excessive». Plus tard en 1969, Minsky et Papert ont expliqué les limites des réseaux à 3 couches, y compris l'incapacité d'apprendre une simple fonction XOR. Mais ils ont noté une solution potentielle: «Les expérimentateurs ont trouvé un moyen intéressant de contourner cette difficulté en introduisant des chaînes plus longues d'unités intermédiaires» (c'est-à-dire en construisant des réseaux de neurones plus profonds). Malgré cette solution de contournement potentielle, une grande partie du travail académique dans ce domaine a été abandonnée.car à cette époque, il n'y avait tout simplement pas assez de puissance de calcul.
Au cours des décennies qui ont suivi, les améliorations du matériel ont entraîné des gains de performances d'environ 50 000 fois, et les réseaux de neurones ont proportionnellement augmenté leurs besoins de calcul, comme le montre KDPV. Étant donné que l'augmentation de la puissance de calcul d'un dollar correspond à peu près à la puissance de calcul par puce, les coûts économiques de fonctionnement de tels modèles sont restés largement stables au fil du temps.
Malgré une telle accélération du processeur, les modèles d'apprentissage en profondeur étaient encore trop lents pour les applications à grande échelle en 2009. Cela a obligé les chercheurs à se concentrer sur des modèles à plus petite échelle ou à utiliser moins d'exemples de formation.
Le tournant a été le transfert du deep learning vers le GPU, qui a immédiatement accéléré5-15 fois , ce qui en 2012 était passé à 35 fois et qui a conduit à une victoire importante pour AlexNet dans le concours Imagenet 2012 . Mais la reconnaissance d'image n'était que la première référence où les systèmes d'apprentissage en profondeur ont gagné. Ils ont rapidement gagné en détection d'objets, en reconnaissance d'entités nommées, en traduction automatique, en réponses aux questions et en reconnaissance vocale.
L'adoption de l'apprentissage profond sur les GPU (puis les ASIC) a conduit à une adoption généralisée de ces systèmes. Mais la quantité de puissance de calcul des systèmes ML modernes a augmenté encore plus rapidement, environ 10 fois par an de 2012 à 2019. Cette vitesse est beaucoup plus élevée que l'amélioration globale du passage aux GPU, le gain modeste du dernier soupir de la loi de Moore ou l'amélioration de l'efficacité de la formation des réseaux neuronaux.
Au lieu de cela, la principale augmentation de l'efficacité du ML provenait de l'exécution de modèles pendant de plus longues périodes sur plus de machines. Par exemple, en 2012, AlexNet s'est entraîné sur deux GPU pendant 5 à 6 jours, en 2017 ResNeXt-101 s'est entraîné sur huit GPU pendant plus de 10 jours, et en 2019 NoisyStudent s'est formé sur un millier de TPU pendant 6 jours. Un autre exemple extrême est le système de traduction automatique Evolved Transformer , qui a utilisé plus de 2 millions d'heures GPU en formation, ce qui a coûté des millions de dollars.
Faire évoluer les calculs d'apprentissage profond en augmentant les horloges matérielles ou le nombre de puces est problématique à long terme. Parce que cela implique que les coûts évoluent à peu près au même rythme que les augmentations de la puissance de calcul, ce qui rend rapidement la croissance impossible.
Futur
Triste conclusion de ce qui précède.
Le tableau suivant montre la puissance de calcul et le coût du système permettant d'atteindre certains objectifs dans les problèmes de ML, si nous extrapolons à partir des modèles actuels. Les tâches d'apprentissage automatique s'exécuteront sur les supercalculateurs les plus puissants. Les auteurs des travaux scientifiques estiment que les exigences relatives aux objectifs fixés ne seront pas remplies . Bien qu'ils envisagent des options théoriquement possibles pour les atteindre: améliorer l'efficacité sans augmenter les performances, les accélérateurs matériels tels que TPU et FPGA, l'informatique neuromorphique, l'informatique quantique et autres, aucune de ces technologies ne permet (encore) de dépasser les limites de calcul du ML.

. .
