Nous analysons les relations causales des métriques VK

Bonjour à tous, je m'appelle Anver, je travaille dans l'équipe Core ML VK. L'une de nos tâches est de créer et d'améliorer des algorithmes de classement pour le fil d'actualité. Dans cet article, je vais vous montrer comment utiliser l'analyse de cause à effet pour rendre le service plus intéressant pour vos utilisateurs. Parlons des avantages de cette approche par rapport à l'analyse de corrélation, et je proposerai des modifications aux algorithmes existants.

Que sont les métriques courtes et longues?

Les modèles de classement tentent d'estimer la probabilité que l'utilisateur interagisse avec les actualités (post): il y prêtera attention, mettra une marque «J'aime», rédigera un commentaire. Le modèle distribue ensuite les enregistrements dans l'ordre décroissant de cette probabilité. Par conséquent, en améliorant le classement, nous pouvons obtenir une augmentation du CTR (taux de clics) des actions des utilisateurs: likes, commentaires et autres. Ces métriques sont très sensibles aux changements du modèle de classement. Je les appellerai courts .



Mais il existe un autre type de métrique. On pense, par exemple, que le temps passé dans l'application, ou le nombre de sessions utilisateur, reflètent bien mieux son attitude envers le service. Nous appellerons ces métriques longtemps .



Optimiser les métriques longues directement via des algorithmes de classement n'est pas une tâche triviale. Avec des métriques courtes, c'est beaucoup plus facile: le CTR des likes, par exemple, est directement lié à la façon dont nous estimons leur probabilité. Mais si nous connaissons les relations causales (ou causales) entre les métriques courtes et longues, nous pouvons alors nous concentrer sur l'optimisation uniquement des métriques courtes qui devraient affecter de manière prévisible les métriques longues. J'ai essayé d'extraire de tels liens causaux - et j'en ai écrit dans mon travail, que j'ai obtenu en tant que diplôme au Bachelor of Science (CT) de l'ITMO. Nous avons mené les recherches dans le laboratoire d'apprentissage automatique de l'ITMO avec VKontakte.

Liens vers le code, le jeu de données et le bac à sable

Vous pouvez trouver tout le code ici: AnverK .



Pour analyser la relation entre les métriques, nous avons utilisé un ensemble de données qui comprend les résultats de plus de 6000 tests A / B réels qui ont été menés par l'équipe VK à différents moments. L'ensemble de données est également disponible dans le référentiel .



Dans le bac à sable, vous pouvez voir comment utiliser le wrapper proposé: sur des données synthétiques .

Et ici - comment appliquer des algorithmes à un ensemble de données: sur l'ensemble de données proposé .

Gérer les fausses corrélations

Il peut sembler que pour résoudre notre problème, il suffit de calculer les corrélations entre les métriques. Mais ce n'est pas tout à fait vrai: la corrélation n'est pas toujours une causalité. Disons que nous ne mesurons que quatre métriques et que leurs relations causales ressemblent à ceci:





Sans perte de généralité, supposons qu'il y ait une influence positive dans le sens de la flèche: plus il y a de likes, plus il y a de SPU. Dans ce cas, il sera possible d'établir que les commentaires sur la photo ont un effet positif sur le SPU. Et décidez que si vous «augmentez» cette métrique, le SPU augmentera. Ce phénomène s'appelle la fausse corrélation.: Le coefficient de corrélation est assez élevé, mais il n'y a pas de relation causale. Les fausses corrélations ne se limitent pas à deux effets de la même cause. À partir de la même colonne, on pourrait tirer la mauvaise conclusion que les likes ont un effet positif sur le nombre d'ouvertures de photos.



Même avec un exemple aussi simple, il devient évident qu'une simple analyse des corrélations conduira à de nombreuses conclusions erronées. L'inférence causale (méthodes d'inférence de relations) permet de restaurer des relations causales à partir de données. Pour les appliquer dans la tâche, nous avons choisi les algorithmes d'inférence causale les plus appropriés, implémenté des interfaces python pour eux, et également ajouté des modifications d'algorithmes connus qui fonctionnent mieux dans nos conditions.

Algorithmes classiques pour les liens d'inférence

Nous avons examiné plusieurs méthodes d'inférence causale: PC (Peter et Clark), FCI (Fast Causal Inference) et FCI + (similaire à FCI d'un point de vue théorique, mais beaucoup plus rapide). Vous pouvez les lire en détail dans ces sources:

• Causalité (J. Pearl, 2009),
• Causation, prédiction et recherche (P. Spirtes et al., 2000),
• L'apprentissage de modèles causaux clairsemés n'est pas une tâche difficile (T. Claassen et al., 2013).

Mais il est important de comprendre que la première méthode (PC) suppose que nous observons toutes les quantités qui affectent deux métriques ou plus - cette hypothèse est appelée suffisance causale. Les deux autres algorithmes tiennent compte du fait qu'il peut y avoir des facteurs non observables qui affectent les métriques surveillées. Autrement dit, dans le second cas, la représentation causale est considérée comme plus naturelle et permet la présence de facteurs non observables$$$U_1, \dots U_k$:







Toutes les implémentations de ces algorithmes sont fournies dans la bibliothèque pcalg . C'est beau et flexible, mais avec un "inconvénient" - il est écrit en R (lors du développement des fonctions les plus lourdes en calcul, le package RCPP est utilisé). Par conséquent, pour les méthodes ci-dessus, j'ai écrit des wrappers dans la classe CausalGraphBuilder, en ajoutant des exemples de son utilisation.



Je décrirai les contrats de la fonction d'inférence de liens, c'est-à-dire l'interface et le résultat qui peut être obtenu en sortie. Vous pouvez passer une fonction de test d'indépendance conditionnelle. C'est un test comme celui-ci qui renvoie$$$p_{value}$ sous l'hypothèse nulle que les quantités $$$X$ et $$$Y$ conditionnellement indépendant pour un ensemble connu de grandeurs $$$Z$... La valeur par défaut est un test de corrélation partielle . J'ai choisi la fonction avec ce test car c'est la fonction par défaut dans pcalg et est implémentée dans RCPP - cela la rend rapide dans la pratique. Vous pouvez également transférer$$$p_{value}$, à partir duquel les sommets seront considérés comme dépendants. Pour les algorithmes PC et FCI, vous pouvez également définir le nombre de cœurs de processeur, si vous n'avez pas besoin d'écrire un journal de l'opération de la bibliothèque. Il n'y a pas une telle option pour FCI +, mais je recommande d'utiliser cet algorithme particulier - il gagne en vitesse. Autre nuance: FCI + ne prend actuellement pas en charge l'algorithme d'orientation des bords proposé - le problème réside dans les limitations de la bibliothèque pcalg.



Sur la base des résultats du travail de tous les algorithmes, un PAG (graphe ancestral partiel) est construit sous la forme d'une liste d'arêtes. Avec l'algorithme PC, il doit être interprété comme un graphe causal au sens classique (ou réseau bayésien): une arête orientée à partir de$$$A$ à $$$B$, signifie influence $$$A$ sur $$$B$... Si l'arête est non directionnelle ou bidirectionnelle, nous ne pouvons pas l'orienter de manière unique, ce qui signifie:

• ou les données disponibles sont insuffisantes pour établir une direction
• ou c'est impossible, car le véritable graphe causal, en utilisant uniquement des données observables, ne peut être établi que jusqu'à une classe d'équivalence.

Les algorithmes FCI donneront également PAG, mais un nouveau type d'arêtes y apparaîtra - avec un "o" à la fin. Cela signifie que la flèche peut ou non être là. Dans ce cas, la différence la plus importante entre les algorithmes FCI et PC est qu'une arête bidirectionnelle (avec deux flèches) indique clairement que les sommets qu'il connecte sont les conséquences de certains sommets non observables. En conséquence, une double arête dans l'algorithme PC ressemble maintenant à une arête avec deux extrémités "o". Une illustration d'un tel cas se trouve dans le bac à sable avec des exemples synthétiques.

Modification de l'algorithme d'orientation des bords

Les méthodes classiques présentent un inconvénient majeur. Ils admettent qu'il peut y avoir des facteurs inconnus, mais en même temps, ils s'appuient sur une autre hypothèse trop sérieuse. Son essence est que la fonction de test d'indépendance conditionnelle doit être parfaite. Sinon, l'algorithme n'est pas responsable de lui-même et ne garantit ni l'exactitude ni l'exhaustivité du graphe (le fait que plus d'arêtes ne peuvent pas être orientées sans violer l'exactitude). Combien de tests d'indépendance conditionnelle à échantillon fini idéal connaissez-vous? Pas moi.



Malgré cet inconvénient, les squelettes de graphes sont construits de manière assez convaincante, mais ils sont orientés de manière trop agressive. J'ai donc suggéré une modification de l'algorithme d'orientation des bords. Bonus: il permet d'ajuster implicitement le nombre d'arêtes orientées. Pour expliquer clairement son essence, il faudrait ici parler en détail des algorithmes de dérivation des liens causaux. Par conséquent, je vais attacher la théorie de cet algorithme et la modification proposée séparément - un lien vers le matériel sera à la fin de l'article.

Comparer les modèles - 1: Estimation de la probabilité du graphique

Curieusement, l'une des graves difficultés à établir des liens de causalité est la comparaison et l'évaluation des modèles. Comment est-ce arrivé? Le fait est que la véritable représentation causale des données réelles est généralement inconnue. De plus, on ne peut pas le connaître en termes de distribution avec une précision suffisante pour en générer des données réelles. Autrement dit, la vérité terrain est inconnue pour la plupart des ensembles de données. Par conséquent, un dilemme se pose: utiliser des données (semi-) synthétiques avec une vérité terrain connue, ou essayer de se passer de vérité terrain, mais tester sur des données réelles. Dans mon travail, j'ai essayé de mettre en œuvre deux approches de test.



Le premier est l'estimation de la probabilité du graphique:







Ici$$$PA_G(X)$ - de nombreux parents de vertex $$$X$, $$$I(X, Y)$ - information conjointe des quantités $$$X$ et $$$Y$, et $$$H(X)$ Est l'entropie de la quantité $$$X$... En fait, le deuxième terme ne dépend pas de la structure du graphique, par conséquent, en règle générale, seul le premier est considéré. Mais vous pouvez voir que la probabilité ne diminue pas avec l'ajout de nouvelles arêtes - cela doit être pris en compte lors de la comparaison.



Il est important de comprendre qu'une telle évaluation ne fonctionne que pour comparer les réseaux bayésiens (sortie de l'algorithme PC), car dans les PAG réels (sortie des algorithmes FCI, FCI +), les doubles arêtes ont une sémantique complètement différente.



Par conséquent, j'ai comparé l'orientation des arêtes avec mon algorithme et le PC classique: L'







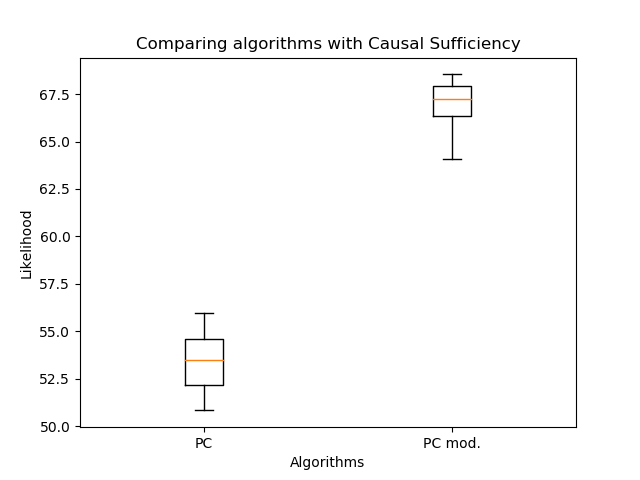
orientation modifiée des arêtes a permis une augmentation significative de la vraisemblance par rapport à l'algorithme classique. Mais maintenant, il est important de comparer le nombre d'arêtes:







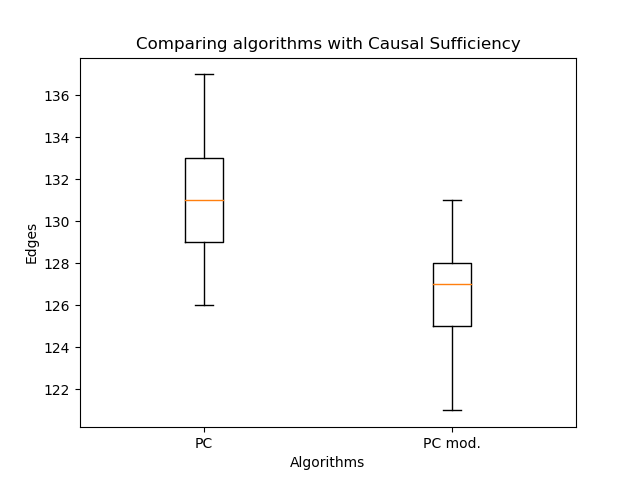
Il y en a encore moins - c'est normal. Ainsi, même avec moins d'arêtes, il est possible de récupérer une structure de graphe plus plausible! Ici, vous pourriez affirmer que la probabilité ne diminue pas avec le nombre d'arêtes. Le fait est que le graphe résultant dans le cas général n'est pas un sous-graphe du graphe obtenu par l'algorithme PC classique. Des arêtes doubles peuvent apparaître au lieu d'arêtes simples, et des arêtes simples peuvent changer de direction. Donc pas d'artisanat!

Comparaison de modèles - 2: Utilisation d'une approche de classification

Passons à la deuxième manière de comparaison. Nous utiliserons l'algorithme PC pour construire un graphe causal et en sélectionner un graphe acyclique aléatoire. Après cela, nous générerons les données à chaque sommet comme une combinaison linéaire des valeurs aux sommets parents avec les coefficients$$$\pm[0,2, 0,8]$avec l'ajout du bruit gaussien. J'ai repris l'idée d'une telle génération dans l'article «Vers une découverte causale robuste et polyvalente pour les applications métier» (Borboudakis et al., 2016). Les sommets qui n'ont pas de parents ont été générés à partir d'une distribution normale - avec des paramètres comme dans le jeu de données pour le sommet correspondant.



Lorsque les données sont reçues, nous leur appliquons les algorithmes que nous souhaitons évaluer. De plus, nous avons déjà un véritable graphe causal. Il ne reste plus qu'à comprendre comment comparer les graphiques résultants avec le vrai. Dans «Reconstruction robuste de modèles graphiques causaux basés sur des informations conditionnelles à 2 et 3 points» (Affeldt et al., 2015), il a été suggéré d'utiliser une terminologie de classification. Nous supposerons que l'arête dessinée est une classe positive et que l'arête non dessinée est négative. Puis vrai positif ($$$TP$) C'est quand nous avons dessiné le même bord que dans le vrai graphe causal, et Faux positif ($$$FP$) - si une arête est dessinée qui n'est pas dans le vrai graphe causal. Nous évaluerons ces valeurs du point de vue du squelette.



Pour prendre en compte les directions, nous introduisons$$$TP_{misorient}$pour les arêtes affichées correctement, mais dans la mauvaise direction. Après cela, nous le considérerons comme ceci:

• $$$TP' = TP - TP_{misorient}$
• $$$FP' = FP + TP_{misorient}$

Ensuite, vous pouvez lire $$$F_1$-taille à la fois pour le squelette et en tenant compte de l'orientation (évidemment, dans ce cas, elle ne sera pas supérieure à celle du squelette). Cependant, dans le cas de l'algorithme PC, une double arête ajoute à$$$TP_{misorient}$ seulement $$$0.5$, mais non $$$1$, car l'un des bords réels est toujours déduit (sans la suffisance causale, ce serait faux).



Enfin, comparons les algorithmes:







Les deux premiers graphiques sont une comparaison des squelettes de l'algorithme PC: le classique et avec la nouvelle orientation des bords. Ils sont nécessaires pour montrer la bordure supérieure$$$F_1$-les mesures. Les deux seconds comparent ces algorithmes en ce qui concerne l'orientation. Comme vous pouvez le voir, il n'y a pas de victoire.

Comparer les modèles - 3: désactiver la suffisance causale

Maintenant, "fermons" certaines variables dans le vrai graphe et dans les données synthétiques après génération. Cela désactivera la suffisance causale. Mais il faudra comparer les résultats non pas avec le vrai graphe, mais avec celui obtenu comme suit:

• les arêtes des parents du sommet caché seront dessinées vers ses enfants,
• connectez tous les enfants du sommet caché avec une double arête.

Nous comparerons déjà les algorithmes FCI + (avec une orientation de bord modifiée et avec le classique):







Et maintenant, lorsque la suffisance causale n'est pas atteinte, le résultat de la nouvelle orientation devient bien meilleur.



Une autre observation importante est apparue: les algorithmes PC et FCI construisent en pratique des squelettes presque identiques. Par conséquent, j'ai comparé leur sortie à l'orientation des bords, que j'ai proposée dans mon travail.







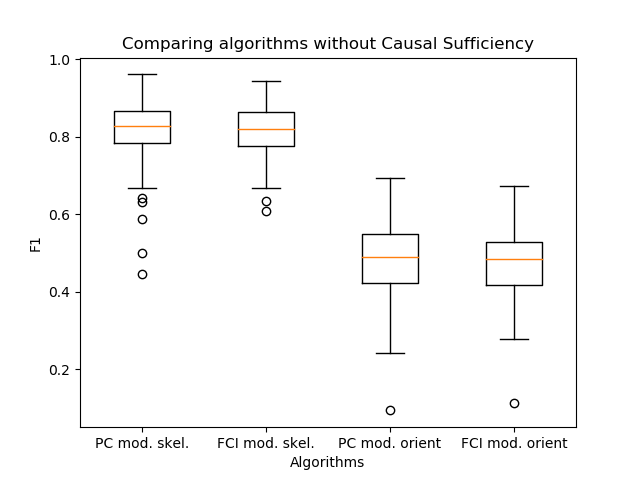
Il s'est avéré que les algorithmes ne diffèrent pratiquement pas en qualité. Dans ce cas, PC est une étape de l'algorithme de construction du squelette à l'intérieur du FCI. Ainsi, l'utilisation de l'algorithme d'orientation PC, comme dans l'algorithme FCI, est une bonne solution pour augmenter la vitesse d'inférence de lien.

Production

Je vais résumer brièvement ce dont nous avons parlé dans cet article:

1. Comment la tâche de dériver des liens de causalité peut survenir dans une grande entreprise informatique.
2. Que sont les corrélations fausses et comment elles peuvent interférer avec la sélection des fonctionnalités.
3. Quels algorithmes pour les liens d'inférence existent et sont utilisés le plus souvent.
4. Quelles difficultés peuvent survenir lors de la création de graphes causaux?
5. Quelle est la comparaison des graphes causaux et comment y faire face.

Si vous êtes intéressé par le sujet de l'inférence causale, consultez mon autre article - il contient plus de théorie. Là, j'écris en détail sur les termes de base qui sont utilisés dans l'inférence des liens, ainsi que sur le fonctionnement des algorithmes classiques et l'orientation des arêtes que j'ai proposé.