La puissante technologie de résolution SAT peut fonctionner avec la tristement célèbre hypothèse de Collatz. Cependant, les chances de cela ne sont pas très élevées.

Au cours des dernières années, Mariin Hijul a utilisé une technologie de recherche de preuves informatisée appelée solveur SAT (SAT pour satisfiability) pour conquérir une liste impressionnante de problèmes mathématiques. Pythagore triple en 2016, Schur numéro 5 en 2017, et récemment l'hypothèse de Keller dans la septième dimension, dont nous avons parlé il n'y a pas si longtemps dans l'article " La recherche informatique a permis de résoudre un problème mathématique vieux de 90 ans ".
Aujourd'hui, cependant, Hijul, informaticien à l'Université Carnegie Mellon, a jeté son dévolu sur un objectif encore plus ambitieux: la conjecture de Collatz, considérée par beaucoup comme le problème ouvert le plus difficile en mathématiques (et sans doute le plus simple à formuler). D'autres mathématiciens, apprenant de moi que Khiyul faisait une telle tentative, étaient sceptiques à ce sujet.
«Je ne vois pas comment ce problème peut être résolu complètement avec le solveur SAT», a déclaré Thomas Hales de l’université de Pittsburgh, un expert de premier plan en matière de preuves informatiques. Cette technologie aide essentiellement les mathématiciens à résoudre des problèmes - dont certains ont un nombre infini d'options - en les transformant en problèmes discrets et finis.
Cependant, Hales, comme les autres, se méfiait de sous-estimer Khiyul. «Il est très doué pour trouver des moyens intelligents de formuler des problèmes dans le langage SAT. Il est très bon dans ce domaine. "
Scott Aaronsonde l'Université du Texas à Austin, travaillant avec Hiyul sur la conjecture de Collatz, a ajouté: «Marin est un homme avec un marteau, c'est-à-dire avec un solveur SAT, et est probablement le plus digne porteur de ce marteau dans le monde entier. Et il essaie de l'appliquer à presque tout. " Mais seul le temps dira s'il peut transformer l'hypothèse Collatz en un clou.
La solution SAT nécessite de reformuler les problèmes dans un langage compréhensible par ordinateur qui utilise la logique propositionnelle , puis de connecter des ordinateurs pour décider s'il existe un moyen de rendre ces déclarations vraies. Voici un exemple simple.
Disons que vous êtes un parent qui essaie d'organiser la garde d'enfants. Une de vos nounous peut travailler toute la semaine sauf le mardi et le jeudi. L'autre est en dehors du mardi et du vendredi. Le troisième - sauf jeudi et vendredi. Vous devez vous asseoir avec votre enfant le mardi, jeudi et vendredi. Cela peut-il être réalisé?
Une façon de tester ceci est de transformer les contraintes de nounou en une formule et de la transmettre au solveur SAT. Le programme cherchera un moyen de répartir les jours entre les nounous afin que la formule se révèle vraie, ou «satisfaite», c'est-à-dire que vous ayez les trois jours dont vous avez besoin. En cas de succès, une telle méthode existera.
Malheureusement, il n'est pas immédiatement clair comment reformuler plusieurs des questions mathématiques les plus importantes en langage SAT. Mais parfois, elles peuvent être reformulées comme des questions de satisfaction de manière inattendue.
«Il est difficile de prédire quand la tâche sera réduite à un calcul énorme mais fini», a déclaré Aaronson.
La conjecture de Collatz est l'une de ces questions mathématiques qui, à première vue, ne semblent pas du tout être un problème de nounou. Elle suggère ce qui suit: prenez n'importe quel nombre (entier, non nul). Si c'est impair, multipliez-le par 3 et ajoutez 1. Si c'est pair, divisez par 2. En conséquence, vous obtenez un nouveau nombre. Appliquez-lui les mêmes règles et continuez. L'hypothèse prédit que quel que soit le numéro de départ, vous vous retrouvez avec 1, puis vous vous retrouvez coincé dans une boucle: 1, 4, 2, 1.
Et, malgré le fait que cette hypothèse ait été élaborée depuis près de 100 ans, les mathématiciens n'ont pas failli la prouver.
Mais cela n'a pas arrêté Khiyul. En 2018, lui et Aronson - tout en étant collègues universitaires - ont reçu une subvention de la National Science Foundation pour appliquer le solveur SAT à la conjecture de Collatz.
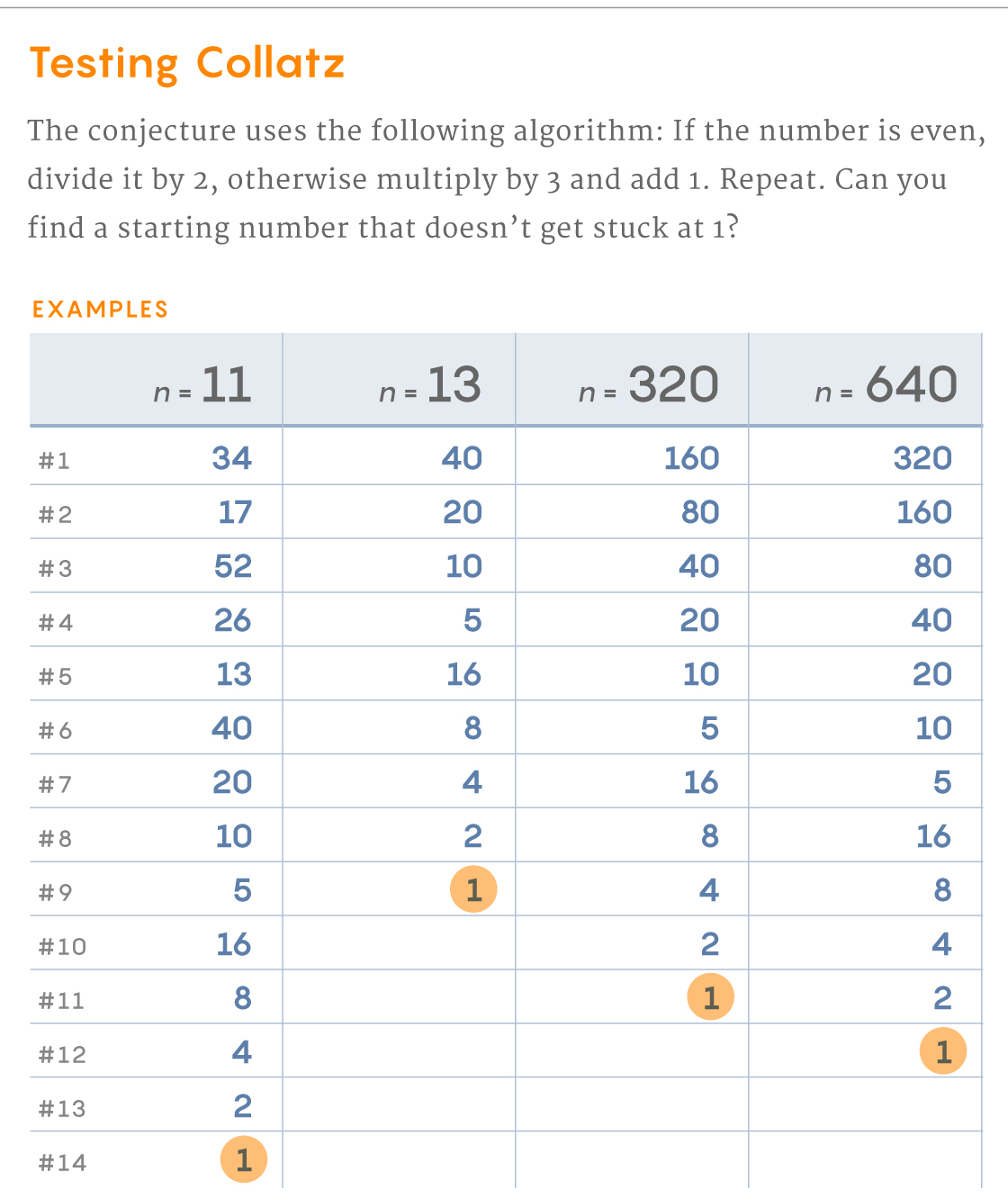
Prenez n'importe quel numéro. Si c'est impair, multipliez-le par 3 et ajoutez 1. Si c'est pair, divisez par 2. En conséquence, vous obtenez un nouveau nombre. Appliquez-lui les mêmes règles et continuez. Pouvez-vous trouver un nombre qui ne mène pas à 1? Vous pouvez l' essayer vous-même .
Pour commencer, Aaronson, un informaticien, a proposé une formulation alternative de l'hypothèse de Collatz, la soi-disant. Un «système de règles de substitution» qui facilite le travail des ordinateurs.
Dans un système de règles de substitution, vous travaillez avec un jeu de caractères, tels que les lettres A, B et C. Vous les utilisez pour former des séquences: ACACBACB. Vous avez également des règles pour convertir ces séquences. Une règle peut dire que lorsque vous rencontrez un AC, vous le remplacez par BC. D'autres peuvent remplacer l'avion par AAA. Vous pouvez définir un nombre illimité de règles définissant toutes les transformations.
Les informaticiens ont généralement besoin de savoir si une JV donnée aboutit toujours. Autrement dit, quelle que soit la ligne de départ et dans quel ordre appliquer les règles, est-il vrai que la ligne finira par se transformer en un état dans lequel aucune règle ne peut être appliquée?
Aaronson a proposé un SP avec sept symboles et 11 règles, similaire à l'hypothèse de Collatz. S'ils peuvent prouver que sa JV se termine toujours, ils prouveront ainsi que l'hypothèse est correcte.
Pour transformer la conjecture de Collatz en un problème de résolution SAT, Aaronson et Hiyul ont dû franchir une autre étape impliquant des matrices, ou des tableaux de nombres. Ils devaient attribuer une matrice unique à chaque symbole de leur SP. Cette approche - une manière courante de chercher la preuve que le SP termine le travail - leur permettrait de raisonner sur les transformations de nombres par multiplication matricielle. Sept matrices désignant sept symboles avec SP devaient satisfaire tout un ensemble de contraintes, reflétant la correspondance de 11 règles entre elles.
"Tout d'abord, vous essayez de trouver des matrices qui satisfont ces contraintes", a déclaréEmre Yolchu , doctorant à l'Université Carnegie Mellon, travaille sur ce problème avec Hijul. «Si vous réussissez, vous prouvez que l'exécution s'arrête», et donc que l'hypothèse de Collatz est correcte.
Le solveur SAT peut répondre à la question de l'existence de matrices satisfaisant ces contraintes. Aaronson et Hijul ont d'abord exécuté le solveur SAT sur de petites matrices 2x2. Ils n'ont pas trouvé d'options de travail. Ensuite, ils ont essayé des matrices 3x3. Et encore une fois en vain. Ils ont continué à augmenter la taille des matrices dans l'espoir de pouvoir les trouver.
Cependant, cette approche ne peut pas se développer indéfiniment, car la complexité de la recherche de matrices appropriées croît exponentiellement avec leur taille. Hijul suggère que les ordinateurs modernes ne peuvent tout simplement pas gérer des matrices plus grandes que 12x12.
«Lorsque les matrices deviennent trop complexes, vous ne pouvez pas résoudre le problème», dit-il.
Hijul travaille toujours à l'optimisation de la recherche, essayant de la rendre plus efficace afin que le solveur SAT puisse vérifier des matrices de plus en plus grandes. Elle et ses collègues travaillent sur un article résumant leurs découvertes actuelles, mais ils sont presque à court d'idées et devront probablement abandonner bientôt - au moins pour un moment.
Après tout, l'attrait du solveur SAT est que si vous pouviez seulement trouver comment vérifier un autre cas, appeler une autre nounou, étendre la recherche même pendant un petit moment, vous pourriez probablement trouver ce que vous cherchiez. En ce sens, le principal avantage de Khiyul n'est peut-être pas son expérience avec les solveurs SAT, mais son amour pour la recherche de résultats.
«Je ne suis qu'un optimiste», a-t-il déclaré. "J'ai souvent l'impression que j'ai de la chance, alors j'essaye juste de voir jusqu'où je peux aller."