Options: vol stationnaire put-call, mouvement brownien. Programme éducatif pour un geek, partie 7

C'est la deuxième partie de l'histoire sur les options, où nous traiterons de la montée en flèche des put-call, de la condition d'absence d'arbitrage de marché, de nous familiariser avec les idées de couverture et de réplication, et parler de ce qu'est le mouvement brownien et de son lien avec la modélisation du comportement du taux d'un actif financier au fil du temps.



Il y aura un peu de calcul pour avoir une meilleure compréhension des détails.







Cet article est une transcription de mes conférences vidéo " Put-call hover and the condition for the absence of arbitrage ", " Brownian motion ", créées dans le cadre du cours Finmath for Fintech.

Survolez l'appel. Un exemple d'utilisation de la condition de non-arbitrage pour analyser le prix d'un portefeuille d'instruments

Ainsi, à partir de la partie précédente, nous savons à quoi ressemblent les paiements pour une option de vente et d'achat à l'expiration (le moment où le droit fourni par l'option peut être exercé), mais nous aimerions également savoir comment calculer l'option pour d'autres périodes. Pour ce faire, nous devons construire un modèle mathématique en utilisant un appareil mathématique plus complexe. Cependant, avant de faire cela, examinons la relation de parité put-to-call, qui est facile à calculer et très utile en pratique.



Rappelons qu'une option européenne est un contrat en vertu duquel l'acheteur du contrat reçoit le droit, mais non l'obligation, d'acheter ou de vendre un actif sous-jacent à un prix prédéterminé à un moment précis dans le futur.



L'actif sous-jacent peut être une action ou un taux de change. Le taux de marché de l'actif sous-jacent est appelé le spot, et dans les formules, la valeur du spot au moment$$$t$ noté $$$S_t$...



Une option qui donne le droit d'acheter l'actif sous-jacent est appelée une option d'achat. Le droit de vendre est une option de vente. Le prix auquel l'option donne le droit de conclure un accord à l'avenir s'appelle une grève, notée$$$K$...



L'heure préétablie dans le contrat à laquelle l'option peut être utilisée est l'heure d'expiration de l'option (expiration) -$$$T$... La valeur du taux de l'actif sous-jacent à l'échéance est indiquée par$$$S_T$...



Construisons des calendriers de paiement pour l'expiration. Nous avons un certain actif sous-jacent - son prix d'expiration:$$$S_T$ainsi que le paiement $$$P$nous recevons. Les calendriers de paiement seront dans ces coordonnées$$$S_T, P$... Mettons$$$K$- niveau de frappe sur l'axe $$$S_T$...



La première option que nous tirerons est une option d'achat. Nous avons acheté une option d'achat.





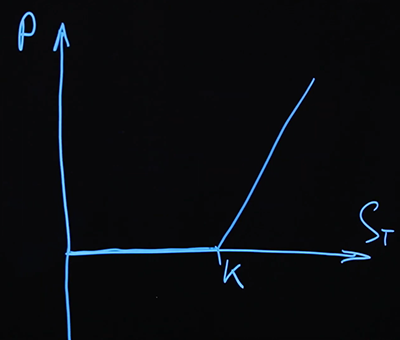
Ceci est également appelé une option d'achat «longue» , une position de signe plus sur cette option. Mais nous pouvons aussi vendre des options, on appelle cela court .



La deuxième option que nous tirerons sera un short put .





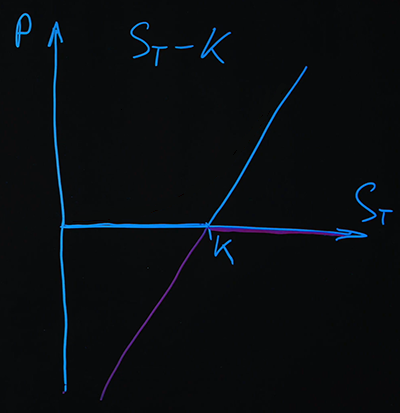
Dans le graphique, nous pouvons voir que lorsque nous avons ajouté les deux paiements, nous avons obtenu une fonction linéaire simple, qui est définie comme ($$$S_T-K$). Le même résultat peut être obtenu analytiquement. Nous avons une position d'option d'achat avec un signe plus et une option de vente avec un signe moins:



$$$C-P$



Utilisons les formules analytiques que nous connaissons déjà:



$$$max(0, S_T-K)-max(0, K-S_T)$...



Pour élargir les crochets, nous devons considérer deux cas distincts où$$$S_T>K$ et $$$S_T<K$...



Nous avons le système suivant:

$$

$$\begin{cases} S_T-K-0, S_T>K \\ 0-K+S_T, S_T≤K \end{cases}$$

Dans les deux cas, vous obtenez la même formule simple: $$$S_T-K$...



Ainsi, les paiements sont dans tous les cas décrits par la même formule, quel que soit le prix de l'actif sous-jacent réalisé au moment de l'expiration. Encore une fois, je vous rappelle que les paiements que nous avons tirés sont des paiements (et donc le coût) des options au moment de l'expiration. Dans le cas des prix d'options à un autre moment, ils sont décrits par d'autres fonctions plus complexes. Je vais les dessiner conditionnellement pour l'instant.





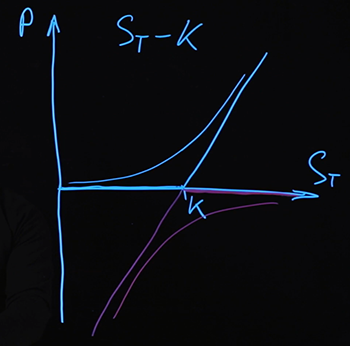
Nous savons que pour cette combinaison au moment de l'expiration, le paiement est déterminé par la formule $$$S_T-K$, pour toute valeur $$$S_T$... Si nous trouvons une autre combinaison d'instruments qui donnera le même paiement au moment de l'expiration, alors nous pouvons dire que le coût d'une telle combinaison d'instruments et de combinaison$$$C-P$devrait être le même.



Si ce n'était pas le cas, vous pouvez aujourd'hui acheter la moins chère de ces combinaisons d'instruments et vendre la plus chère, réalisant ainsi un profit. Et comme ces deux combinaisons donnent le même paiement à l'expiration et que nous les avons prises avec des signes opposés, le paiement total est garanti égal à zéro. Une telle transaction, qui donne un revenu garanti sans risque, simplement en raison du déséquilibre des prix des instruments sur le marché, est appelée arbitrage.... Les théories mathématiques pour calculer les prix des instruments incluent généralement l'hypothèse que le marché est libre d'arbitrage. Cette hypothèse correspond assez bien à la réalité. Les opportunités d'arbitrage sur le marché, si elles se présentent, ne durent pas longtemps. Les trouver et les utiliser n'est pas facile. Donc, normalement, cette hypothèse fonctionne bien.



De la condition que le marché soit exempt d'arbitrage, il s'ensuit que la combinaison$$$C-P$ sera à tout moment $$$t≤T$ (pas seulement $$$T$) coûte le même prix que toute combinaison d'instruments dont le paiement au moment $$$T$ sera égal $$$S_T-K$... Cette combinaison est facile à réaliser en achetant l'actif sous-jacent$$$S$ et emprunter de l'argent d'un montant tel qu'au moment de l'expiration, il sera nécessaire de rembourser un montant égal à $$$K$... Lorsqu'il s'agit d'instruments financiers, une telle dette équivaut à vendre une obligation à coupon zéro (obligation), ce qui donne un paiement$$$K$ en ce moment $$$T$... Vous pouvez en savoir plus sur les obligations et les intérêts dans les articles précédents de cette série ( Valeur de l'argent, types d'intérêts, rabais et taux à terme. Programme éducatif pour un geek, partie 1 et Obligations: coupon et coupon zéro, calcul du rendement. Programme éducatif pour un geek, partie 2 ) ...



Ainsi, un portefeuille d'une option d'achat et un portefeuille d'une option de vente est égal à la combinaison d'un long pour l'actif sous-jacent et d'une obligation courte, ce qui donnerait un paiement par expiration avec un pair$$$K$...



$$$C_t-P_t=S_t-B_TK$



Ce ratio est indépendant du modèle que nous pourrions construire pour le taux d'actif sous-jacent. Cela ne dépend même pas de la façon dont nous envisageons l'actualisation, et cela découle de l'absence d'arbitrage sur le marché. Nous avons compilé un portefeuille, examiné toutes les options possibles, combien cela peut coûter à l'expiration, découvert que dans toutes les options futures, cela coûte exactement le même. Par conséquent, si un autre portefeuille a exactement le même paiement à l'expiration, alors leur prix devrait être le même.



Nous avons donc obtenu le ratio pour un portefeuille d'options d'achat et de vente. Nous avons compilé un portefeuille, examiné le type de paiement qu'il aura au moment de l'expiration, découvert que le paiement est décrit par une équation linéaire. Contrairement à la fonction de paiement pour les options d'achat et de vente, dont chacune comporte deux sections, plus ou moins$$$S_T$... Cela vous permet de créer un portefeuille d'instruments plus simples qui donneront le même paiement à l'expiration dans n'importe quelle situation. Le prix de ces deux portefeuilles sera égal à tout moment, pas seulement au moment de l'expiration. Ceci est garanti par la condition qu'il n'y ait pas d'arbitrage sur le marché. S'il y a arbitrage sur le marché et que cette égalité n'est pas satisfaite, nous pouvons donc acheter l'un de ces portefeuilles, en vendre un autre et obtenir une victoire garantie. Ce ratio ne dépend d'aucun modèle mathématique que l'on pourrait construire, par exemple, pour le prix de l'actif sous-jacent. Ce ratio doit être respecté dans n'importe quel modèle.



Vous pouvez également regarder ce rapport comme ceci. Nous avons constitué un portefeuille de plusieurs actifs présentant le même risque. La formule peut être réécrite pour collecter les actifs qui portent le risque associé à l'actif sous-jacent d'une part. Autrement dit, nous pouvons éliminer tous les risques inhérents à ces instruments, c'est-à-dire l'incertitude associée au prix futur de l'actif sous-jacent, sachant exactement combien vaut un tel package.



$$$C_t-P_t-S_t=-B_tK$



Cette façon de se débarrasser du risque s'appelle la couverture . Nous composons un portefeuille de plusieurs instruments dans lequel une partie du même risque est intégré, mais nous les sélectionnons dans des proportions telles que ces risques s'équilibrent mutuellement et nous nous en débarrassons. Cette idée est utilisée dans d'autres stratégies de couverture plus complexes. Le cas considéré est très simple, il permet de ne travailler qu'avec une certaine combinaison d'options.



Si nous regardons cette idée de l'autre côté, nous pourrions alors exprimer l'un de ces outils à travers d'autres. Par exemple, si nous avons une chose sur le marché, une option de vente, nous recevrons également automatiquement une option d'achat. Dans ce cas, ce sera la réplication- nous avons répliqué le paiement d'un produit par d'autres. La couverture et la réplication sont étroitement liées l'une à l'autre, mathématiquement, ce sont des calculs très similaires.



Dans ce cas, nous avons une situation très simple, et pour couvrir complètement le risque ou répliquer le paiement, il nous suffit de créer un portefeuille une fois, puis nous attendons le moment de l'expiration, le paiement nous est déjà garanti. C'est ce qu'on appelle la réplication statique ( couverture statique). C'est un cas rare et ne fonctionne généralement pas. Pour atteindre cet effet plus généralement, il sera nécessaire de recourir à des stratégies de couverture dynamique. Autrement dit, nous créerons un portefeuille une fois, mais nous devrons constamment y ajouter quelque chose ou y changer quelque chose afin que le paiement au moment de l'expiration se déroule exactement comme nous le souhaitons.



Voici un ratio intéressant de montée en flèche des put-call. Malgré le fait que le calcul soit très simple, dans son exemple, vous pouvez voir plusieurs idées très importantes qui sont appliquées dans un cas plus complexe - l'application de la condition de non-arbitrage, la réplication des paiements et la couverture des risques. C'est là que nous terminons avec cette relation simple et pouvons passer à la construction d'un modèle plus complexe.



Nous souhaitons construire un modèle qui donnerait non seulement le rapport entre les options d'achat et de vente, mais aussi le prix de l'option en fonction des valeurs observées sur le marché. Cela nécessitera une théorie mathématique plus complexe.

Qu'est-ce que le mouvement brownien et qui est Robert Brown. Comment simuler un mouvement brownien sur un ordinateur. Qu'est-ce que le mouvement brownien géométrique

Ce que nous avons envisagé jusqu'à présent nous a permis de nous en sortir avec un appareil mathématique très simple, en fait les mathématiques scolaires. Pour avancer et construire un modèle mathématique plus complexe, cela ne nous suffira pas, et des éléments de mathématiques «adultes» sont nécessaires. Par conséquent, l'approche générale de la présentation ultérieure ressemblera à ceci: je donnerai des exemples illustratifs à partir desquels il sera clair comment l'appareil mathématique fonctionne dans un cas simple, et je donnerai également des formulations et des théorèmes que nous utiliserons. Je ne prouverai pas ces théorèmes. Ceux qui sont intéressés par la partie mathématique peuvent se référer aux manuels et cours vidéo correspondants.



Le premier concept dont nous avons besoin est le mouvement brownien... Rappelons-nous ce que ce terme signifie en physique. Ce sera une sorte d'exemple clair de la façon dont ce processus sera organisé dans notre modèle mathématique formel.



Je pense que beaucoup de gens utilisent le terme « mouvement brownien»associé au programme scolaire de physique. Beaucoup pensent que la personne qui a introduit ce concept dans la circulation scientifique était un physicien du nom de Brown et, à en juger par son nom, était un Anglais. Fait intéressant, toutes ces hypothèses sont fausses. Premièrement, le nom de ce scientifique était Robert Brown, qui en russe devrait être lu comme «Robert Brown». Bien que cela puisse ne pas être évident pour une personne éduquée des XVIIIe et XIXe siècles, dont la première langue étrangère était le français et la seconde l'allemand. Deuxièmement, il n'était pas Anglais - c'était un Écossais, ce qui, comme nous le comprenons, n'est pas du tout la même chose. Mais le plus intéressant, c'est qu'il n'était pas physicien - c'était un botaniste. Lorsqu'il a mené et décrit sa célèbre expérience, il étudiait les particules de pollen au microscope. Le spécimen sur la lame a été préparé sous la forme d'une goutte de liquide, dans laquelle des particules de pollen ont été placées afin deafin que le pollen ne s'envole pas de tous les courants d'air et puisse être vu calmement.



L'attention de Brown a été attirée sur le fait que ce qu'il voit dans l'oculaire du microscope n'est pas une image statique. Il a observé, relativement parlant, une particule ronde qui faisait un mouvement chaotique. Aujourd'hui, nous savons que ce phénomène a une explication simple. Il y a de nombreuses molécules dans la solution autour de cette particule, qui interagissent très souvent avec elle dans une direction aléatoire, à la suite de quoi la particule effectue une sorte de mouvement complexe.





Si nous décrivons son mouvement, ce sera une trajectoire aléatoire.





Qu'est-ce que cela a à voir avec notre domaine? En fait, l'analogie est simple. Nous considérons le taux d'un actif financier dans le temps. De nombreux facteurs aléatoires agissent sur elle, ainsi que sur cette particule, à chaque instant. Nous ne les voyons pas, tout comme Robert Brown n'a pas vu de molécules individuelles au microscope.



L'effet cumulatif de ces facteurs aléatoires conduit à un changement dans le cours de l'actif - tout comme l'effet cumulatif des molécules conduit au déplacement d'une particule de pollen. Ces processus se produisent continuellement dans le temps. Et ainsi le taux de l'actif financier est réalisé. La dépendance du cours au temps est obtenue de manière aléatoire, et donc une telle trajectoire est appelée mouvement brownien. Dans notre cas, il s'agit d'un mouvement brownien unidimensionnel, car des écarts aléatoires ne se produisent que autour d'un axe.





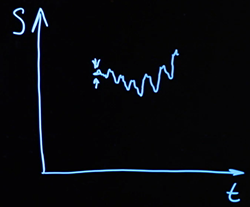
Le modèle mathématique formel du processus que nous utiliserons est associé au nom d'un autre scientifique, le mathématicien américain Norbert Wiener. Ça ressemble à ça. Nous envisageons une fonction de temps continu. Parce que le$$$t$ est continue, alors la fonction $$$W(t)$continu.



Il contient une composante aléatoire, qui est mathématiquement déterminée comme suit:



$$$\triangle W_{\triangle t}$- indépendant à condition que les incréments de temps ne se coupent pas.



Incrément de fonction à partir du point de temps$$$t$ jusqu'au moment $$$t+s$ normalement distribué avec les paramètres 0 et $$$s$ (la longueur de l'intervalle de temps).



$$$W_{t+s}-W_t∼N(0,s)$



Dans ce qui suit, nous verrons qu'il est très important de pouvoir générer de tels chemins sur un ordinateur - c'est nécessaire pour de nombreuses méthodes de calcul. Comment pourrions-nous faire cela? Le temps, qui est continu dans un modèle mathématique théorique, nous divisons sur un ordinateur en quelques incréments, généralement avec un pas fixe. Nous créons un certain point de départ à partir duquel notre processus commence, avec des coordonnées$$$W_0;t_0$... De plus, pour chaque pas de temps suivant, nous générons une variable aléatoire avec une telle distribution, nous nous déplaçons d'un pas. Nous faisons cela à tout moment. Le résultat est une ligne brisée.





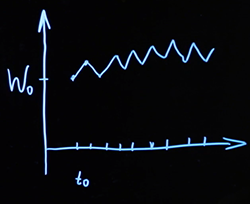
Quelque part, l'incrément s'est avéré avec un signe plus, quelque part avec un signe moins. En conséquence, à chaque point spécifique, la valeur de l'ensemble du processus est déterminée par la somme cumulée de toutes ces variables aléatoires. Afin de pouvoir mettre à l'échelle le déplacement moyen par unité de temps, nous pouvons également introduire un paramètre supplémentaire, généralement désigné par la lettre$$$\sigma$(comme pour la distribution normale). On peut considérer la fonction$$$\sigma W_t$où $$$W_t$ Est le mouvement brownien standard, et $$$W_t$a une variance plus ou moins large, selon ce dont nous avons besoin.



Avec un tel processus en place, nous aimerions construire un modèle mathématique qui nous aiderait à calculer le prix des options. Construisons des équations selon le même principe que nous l'avons fait avec intérêt pour l'actualisation en temps continu. Ce sera une sorte d'équation différentielle.



Si nous résolvions le problème du calcul des intérêts sur un certain montant$$$P$ en temps continu, alors pour un petit pas de temps nous aurions la relation correcte $$$\triangle P=rP\triangle t$ ou



$$$\frac{\triangle P}{P}=r\triangle t$,



où$$$r$Est un taux d'intérêt neutre au risque. Et aller à la limite$$$Δt →d_t$, on obtient l'équation différentielle



$$$\frac{dP}{P}=rdt$...



De là, nous obtenons la formule déjà familière pour l'actualisation en temps continu$$$P=P_0e^{rt}$où $$$P_0$Est la valeur initiale.



Je voudrais adapter cette logique de raisonnement pour un modèle mathématique d'un actif dont le prix dans le futur dépend de facteurs aléatoires. L'évolution relative du prix de notre actif est caractérisée par un certain paramètre, un analogue du taux neutre au risque (dans ce cas, le paramètre caractérise notre actif sous-jacent, ce n'est pas un taux neutre au risque). Ajoutons à cette expression une composante probabiliste qui serait décrite par le mouvement brownien.



$$$\frac{ΔS}{S}=μΔt+σΔW$



Nous avons pratiquement un résultat. Allons à la limite et obtenons une équation très similaire à celle que nous avons facilement résolue pour l'actualisation en temps continu.



$$$\frac{dS}{S}=μdt+σdW$



Mais il y a un problème technique. Le fait est que le mouvement brownien (processus de Wiener), tel que nous l'avons défini, est une fonction continue du temps, mais il n'est pas différentiable au sens de l'analyse mathématique classique. Cela peut être prouvé formellement (nous omettons la preuve).



Afin de construire un tel modèle mathématiquement rigoureusement, il est nécessaire de déterminer quel sens on met dans l'expression$$$dW$... Pour cela, il est nécessaire d'utiliser un différentiel stochastique, dont le nom est associé au nom d'un autre mathématicien - le différentiel Ito . Il obéit à des règles différentes de celles auxquelles nous sommes habitués dans le calcul conventionnel.



Pour référence, j'écrirai les résultats dont nous avons besoin concernant cet appareil mathématique. Le différentiel Ito obéit à de telles règles.



Si



$$$dx=a(x,t)dt+b(x,t)dW_t$,



puis pour $$$f(x,t)$:



$$$df=\frac{∂f}{∂t}dt+\frac{∂f}{∂x}dx+\frac{1}{2}\frac{∂^2f}{∂x^2}dx^2$...



Cette règle diffère de la façon dont nous différencions une fonction de deux variables dans le calcul conventionnel. Si nous avons deux variables indépendantes, dans le calcul ordinaire, nous prenons des dérivées partielles et nous nous arrêtons aux deux premiers termes de l'expansion. La troisième composante de l'expansion du différentiel d'une fonction dans la formule Ito apparaît précisément parce que nous ne travaillons pas avec des fonctions ordinaires, mais avec un processus aléatoire et stochastique. Nous prenons ce résultat tout fait, sans le prouver.



Il y a plus à dire sur$$$dx^2$dans la dernière équation. Par condition$$$dx=a(x,t)dt+b(x,t)dW_t$, si nous la mettons au carré, alors il y aura des termes avec des facteurs $$$dt dW_t$, $$$dt^2$, $$$dW^2_t$... Pour appliquer la formule Ito, vous devez prendre:



$$$dt dW_t=0$; $$$dt^2=0$; $$$dW^2_t=dt$...



Toutes ces règles deviennent naturelles si vous comprenez ce qu'est l'intégrale Ito, mais pour nos besoins, il suffit maintenant de savoir comment appliquer correctement la formule Ito.



Et maintenant nous pouvons surmonter notre complexité technique, puisque nous savons comment opérer avec un objet$$$σdW$...



En tant que variable$$$x$ nous avons le taux d'actif sous-jacent $$$S$, nous pouvons l'exprimer:



$$$dS=Sμdt+σSdW_t$...



Ensuite, on sait écrire le différentiel de la fonction, là où il y a$$$S$ et $$$t$... Voyons quel est le différentiel de la fonction$$$f(S, t)=ln⁡(S)$...



$$$dln S = df = \frac{∂f}{∂t}dt+\frac{∂f}{∂S}dS+\frac{1}{2}\frac{d^2f}{dS^2}dS^2=$



$$$=0 dt+\frac{1}{S}(Sμdt+σSdW_t)-\frac{1}{2}\frac{1}{S^2}\sigma^2 S^2 dt$



Maintenant, en collectant les termes, nous obtenons une expression pour le logarithme $$$S$...



$$$d㏑S=(μ-\frac{\sigma^2}{2})dt+σdW$



Maintenant, nous savons ce qui est égal à $$$㏑S$(notez qu'il a une distribution normale). Nous nous intéressons directement à l'expression pour$$$S$...



$$$S=S_0 e^{μt}exp(σW_t-\frac{\sigma^2}{2}t)$



L'expression ci-dessus décrit le mouvement brownien géométrique . Cela représente une croissance exponentielle avec le paramètre$$$\mu$qui commence initialement au point $$$S_0$, et le bruit se superpose autour de cet exposant selon l'expression $$$exp(\sigma W_t-\frac{\sigma^2}{2}t)$... Cela peut déjà être lu sur un ordinateur, nous pouvons générer des chemins de mouvement brownien. Nous obtiendrons quelques réalisations possibles de notre trajectoire pour le taux d'actif sous-jacent. Il y a deux paramètres dans cette équation:$$$\sigma$ - variance et $$$\mu$- dérive. Ils correspondent à la variance de la distribution normale et au biais de la distribution normale pour$$$㏑S$... Comme je l'ai dit, il est maintenant possible de simuler sur un ordinateur, mais il y a un autre élément théorique que nous devons introduire afin que nous puissions calculer le prix des options en utilisant ce processus. Ensuite, nous parlerons de mesure neutre au risque.



Tous les articles de cette série

• Valeur de l'argent, types d'intérêts, actualisation et taux à terme. Programme éducatif pour un geek, partie 1
• Obligations: coupon et coupon zéro, calcul du rendement. Programme éducatif pour un geek, partie 2
• Obligations: évaluation des risques et cas d'utilisation. Programme éducatif pour un geek, partie 3
• Comment les banques empruntent les unes aux autres. Taux flottants, swaps de taux d'intérêt. Programme éducatif pour un geek, partie 4
• Construction de la courbe d'actualisation. Programme éducatif pour un geek, partie 5
• Quelles sont les options et qui en a besoin. Programme éducatif pour un geek, partie 6
• Options: vol stationnaire put-call, mouvement brownien. Programme éducatif pour un geek, partie 7