🤕 🤳🏿 🎗️ Apprentissage automatique. Réseaux de neurones (partie 3) - Réseau convolutif sous le microscope. Explorer l'API Tensorflow.js 🥋 🈚️ 🛀🏽

Voir également:

Apprentissage automatique. Réseaux de neurones (partie 1): le processus d'apprentissage Perceptron
Apprentissage automatique. Réseaux de neurones (partie 2): modélisation OR, XOR avec TensorFlow.js

Dans les articles précédents, un seul des types de couches de réseau neuronal a été utilisé - dense, entièrement connecté, lorsque chaque neurone de la couche d'origine a une connexion avec tous les neurones des couches précédentes.

Pour gérer une image en noir et blanc 24x24, par exemple, il faudrait transformer la représentation matricielle de l'image en un vecteur contenant 24x24 = 576 éléments. Comme vous pouvez l'imaginer, avec une telle transformation, nous perdons un attribut important - la position relative des pixels dans les directions verticale et horizontale des axes, et aussi, probablement, dans la plupart des cas, le pixel situé dans le coin supérieur gauche de l'image n'a guère d'effet logiquement explicable sur le pixel dans le coin inférieur droit.

Pour éliminer ces inconvénients, des couches convolutives (CNN) sont utilisées pour le traitement d'image.

L'objectif principal de CNN est d'extraire de l'image d'origine de petites parties contenant des éléments (caractéristiques) de support, tels que des arêtes, des contours, des arcs ou des faces. Aux niveaux de traitement suivants, des fragments de textures répétables plus complexes (cercles, formes carrées, etc.) peuvent être reconnus à partir de ces bords, qui peuvent ensuite être pliés en textures encore plus complexes (partie du visage, roue de voiture, etc.).

Par exemple, considérons un problème classique - la reconnaissance d'image des nombres. Chaque numéro a son propre ensemble de chiffres typiques pour eux (cercles, lignes). Dans le même temps, chaque cercle ou ligne peut être composé d'arêtes plus petites (Figure 1)

Figure 1 - Le principe de fonctionnement des couches convolutives connectées séquentiellement, avec l'attribution de traits caractéristiques à chacun des niveaux. Chacune des couches suivantes d'un ensemble de couches CNN en guirlande extrait des modèles plus complexes basés sur ceux précédemment identifiés. — 1 – , . CNN , .

1. (convolutional layer)

CNN ( ), c () , . – CNN – .

, 2x2 ( K) , 2x2 ( N), :

$\ left [\ begin {matrix} n_ {11} & n_ {12} \\ n_ {21} & n_ {22} \\\ end {matrix} \ right] \ ast \ left [\ begin {matrix} k_ {11} & k_ {12} \\ k_ {21} & k_ {22} \\\ end {matrix} \ right] = n_ {11} k_ {11} + n_ {12} k_ {12} + n_ {21} k_ {21 } + n_ {22} k_ {22}$

, .

, (fully-connected, dense layers):

${somme = \ \ vec {X}} ^ T \ vec {W} = \ sum_ {i = 1} ^ {n = 4} {x_iw_i} = x_1w_1 + x_2w_2 + x_3w_3 + x_4w_4$

, - , – - , ( ).

2. , , , .

Figure 2 - Calcul dans les couches convolutives — 2 –

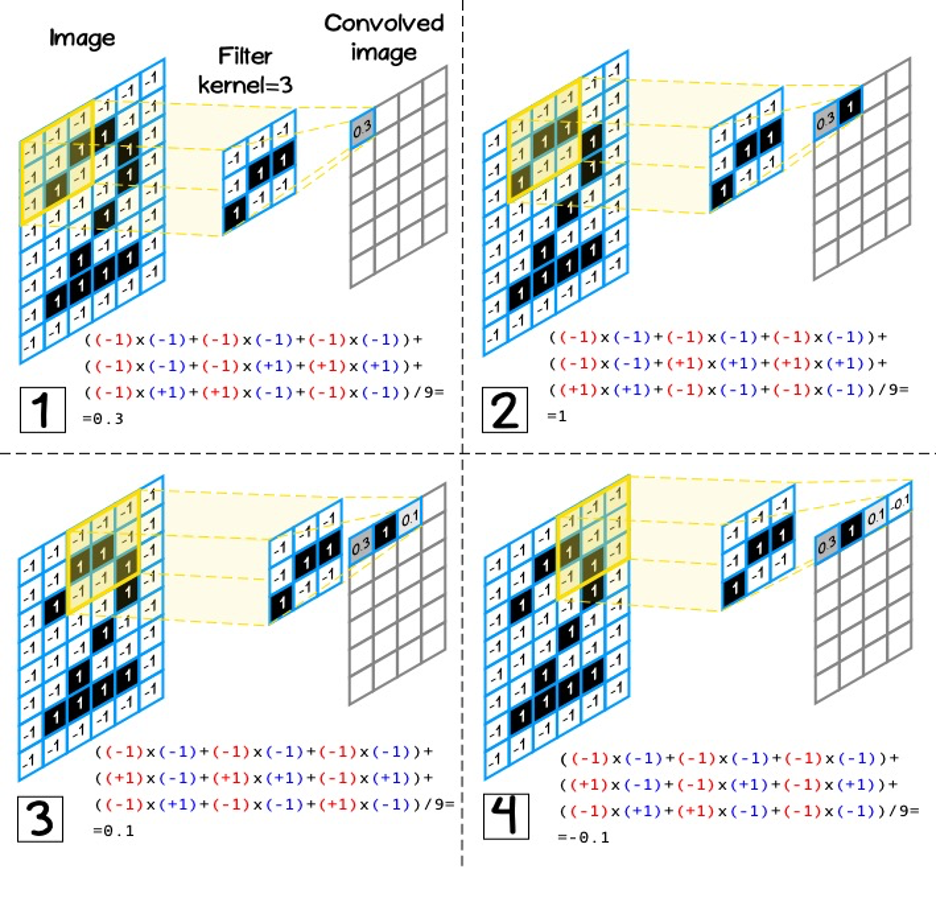
(kernel size) – 3, 5, 7.

(kernel) [k_h, k_w], [n_h, n_w], ( 3):

Figure 3 - Le principe de la formation de la couche de sortie convolutive avec la dimension du noyau de filtre [3,3] — 3 – [3,3]

, . , . , .

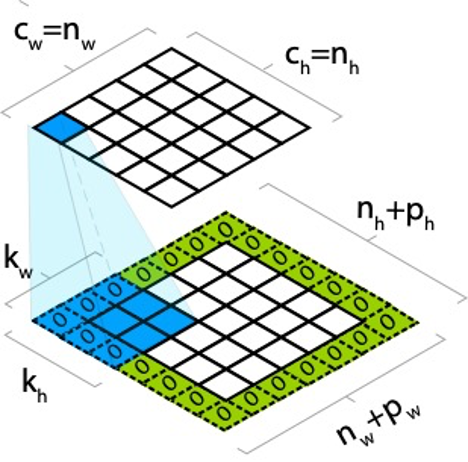
, – (padding). , . , p_h p_w , :

, , , :

- . , (stride). – (stride).

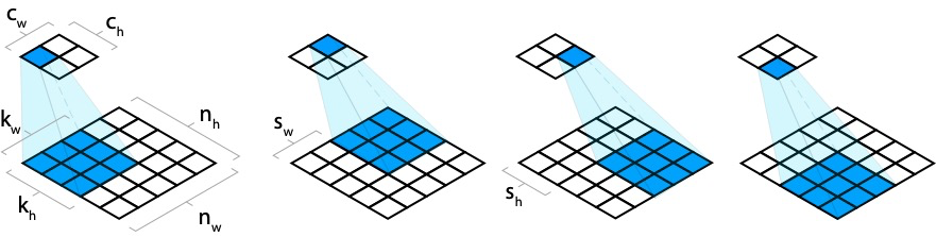
, s_w, s_h, :

$c_w=\left \lfloor (n_w+p_w-k_w+s_w)/s_w \right \rfloor; c_h=\left \lfloor (n_h+p_h-k_h+s_h)/s_h \right \rfloor$

, ( – ). (). , (CONV1) 9x9x1 ( – - ), 2 1x1 (stride) (padding) , , . 9x9x2 2 – (. 6). CONV2 , , 2x2, , 2, 2x2x2. (CONV2) 9x9x4, 4 – .

, k_w k_h , n_wx n_hx n_d, n_d - , , k_w x k_h x n_d ( 6, CONV2).

7 , RGB, 3x3. , (3 ), 3x3x3.

TensorFlow.js

, : tf.layers.conv2d, – , :

- filter – number –

- kernelSize – number | number[] – , number, , –

- strides – number | number[] - , [1,1], .

- padding – ‘same’, ‘valid’ – , ‘valid’

'same'

, , () (stride) . , - 11 , – 5, 13/5=2.6, – 3 ( 8).

stride=1, ( 9), , ( 8).

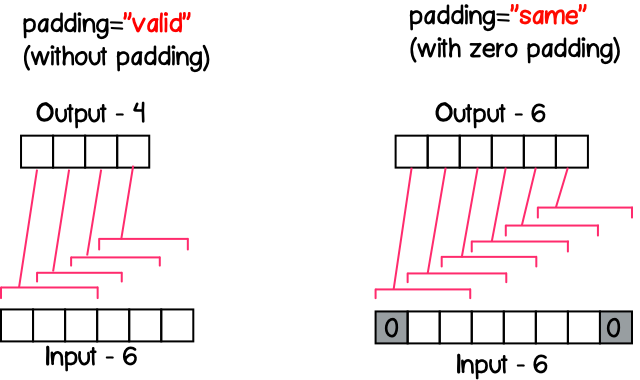
'valid'

, strides , 8.

TensorFlow.js

, . :

- :

$\left[\begin{matrix}1&0&-1\\1&0&-1\\1&0&-1\\\end{matrix}\right]$

- :

$\ left [\ begin {matrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ - 1 & -1 & -1 \\\ end {matrix} \ right]$

, , tf.browser.fromPixels. , img canvas .

<img src="./sources/itechart.png" alt="Init image" id="target-image"/>
<canvas id="output-image-01"></canvas>

<script>
   const imgSource = document.getElementById('target-image');
   const image = tf.browser.fromPixels(imgSource, 1);
</script>

, , , 3x3, “same” ‘relu’:

const model = tf.sequential({
    layers: [
        tf.layers.conv2d({
            inputShape: image.shape,
            filters: 1,
            kernelSize: 3,
            padding: 'same',
            activation: 'relu'
        })
    ]
});

[NUM_SAMPLES, WIDTH, HEIGHT,CHANNEL], tf.browser.fromPixel [WIDTH, HEIGHT, CHANNEL], – ( , ):

const input = image.reshape([1].concat(image.shape));

. , setWeights Layer, :

model.getLayer(null, 0).setWeights([
    tf.tensor([
         1,  1,  1,
         0,  0,  0,
        -1, -1, -1
    ], [3, 3, 1, 1]),
    tf.tensor([0])
]);

, , 0-255, NUM_SAMPLES:

const output = model.predict(input);

const max = output.max().arraySync();
const min = output.min().arraySync();

const outputImage = output.reshape(image.shape)
    .sub(min)
    .div(max - min)
    .mul(255)
    .cast('int32');

canvas, tf.browser.toPixels:

tf.browser.toPixels(outputImage, document.getElementById('output-image-01'));

2. (pooling layer)

, ( ), , . , , (pooling layer, subsample layer), . MaxPooling .

, .

. (kernel) , (stride) 1x1, . , (. 10).

Figure 10 - Transformation dans la couche de sous-échantillon — 10 –

, 4x4, 2x2 (stride) , 2x2, .

, ( 11) . , , MaxPooling . (translation invariance). , , 50%. , , MaxPooling .

Figure 11 - Lissage des déplacements spatiaux après la couche MaxPooling — 11 – MaxPooling

, .

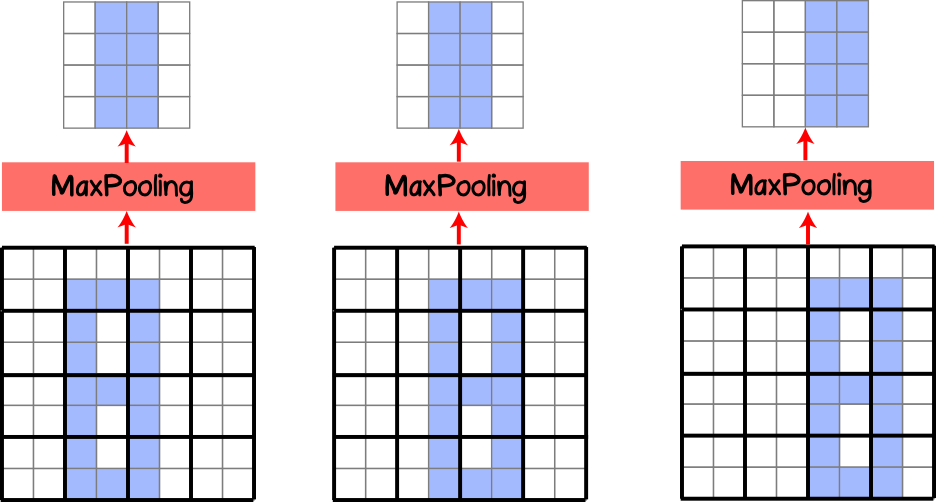
, , – (stride).

MaxPooling AveragePooling, , , . , MaxPooling. AveragePooling , , MaxPooling .

TensorFlow.js (pooling layer)

tf.layers.maxPooling2d tf.layers.averagePooling2d. – , :

- poolSize - nombre | nombre [] - la dimension du filtre, si nombre est spécifié, alors la dimension du filtre prend une forme carrée, si elle est spécifiée sous forme de tableau, la hauteur et la largeur peuvent différer

- foulées - nombre | number [] est un pas en avant, un paramètre facultatif et a par défaut la même dimension que poolSize spécifié.

- padding - 'same', 'valid' - mise à zéro padding, par défaut 'valid'

Apprentissage automatique. Réseaux de neurones (partie 3) - Réseau convolutif sous le microscope. Explorer l'API Tensorflow.js

1. (convolutional layer)

TensorFlow.js

'same'

'valid'

TensorFlow.js

2. (pooling layer)

TensorFlow.js (pooling layer)

More articles: