Révision du protocole cryptographique du système de vote électronique à distance

Dans cet article, nous analyserons les détails de la mise en œuvre du protocole cryptographique du système de vote électronique à distance.



L'utilisation de mécanismes et d'algorithmes cryptographiques à différentes étapes du processus électoral confère au système de vote à distance les propriétés nécessaires. Examinons de plus près et examinons les étapes du vote décrites dans l' article de présentation .



Initialisation du système. Au stade de l'initialisation du vote, les opérations cryptographiques suivantes sont effectuées:

• Développement d'une paire de clés de validation pour l'émission et la vérification d'une signature aveugle, comme la plus persistante et recommandée par la communauté universitaire pour la procédure d'anonymisation dans les systèmes de vote électronique. Pour le moment, le système prend en charge des algorithmes de signature aveugle sur des courbes elliptiques et basés sur l'algorithme de cryptage RSA. Le vote a été effectué à l'aide d'un algorithme d'émission et de vérification d'une signature aveugle basé sur l'algorithme de cryptage RSA avec une longueur de clé de 4096 bits.
• Génération d'une clé de chiffrement publique partagée. Pour une plus grande sécurité dans le processus de génération de clé, deux algorithmes cryptographiques sont utilisés à la fois: le protocole de génération de clé distribuée DKG Pedersen 91 et le protocole de partage de clé Shamir. La génération des clés est réalisée à la fois par des participants qui ont les moyens techniques de contrôler directement les nœuds du réseau et le serveur de comptage, et par des participants qui sont les détenteurs des clés enregistrées sur des supports externes. Le résultat du travail de ces deux algorithmes est une clé publique commune pour le cryptage des bulletins de vote. Ensuite, nous examinerons de plus près la procédure de génération de cette clé.

Donner accès à la newsletter . À ce stade, les mécanismes suivants fonctionnent:

• Génération d'une paire de clés d'une signature électronique sur l'appareil d'un électeur conformément à GOST R 34.10-2012
• Génération d'une signature aveugle pour la clé publique d'un électeur masqué pour la certification et la vérification ultérieure de son droit de vote. Le mécanisme est actuellement basé sur l'algorithme de chiffrement RSA. Le mécanisme d'anonymisation est discuté en détail dans un article séparé.

Remplir et envoyer la newsletter . À ce stade, l'ensemble suivant d'algorithmes cryptographiques est utilisé:

• Cryptage de la courbe elliptique de la newsletter selon le schéma ElGamal. Ce schéma est utilisé dans le protocole, car il a en outre la propriété d'être homomorphe, ce qui permet d'obtenir des résultats de vote sans décrypter chaque bulletin.
• La preuve à distance disjonctive de Chaum-Pedersen est utilisée pour prouver l'exactitude du contenu du bulletin de vote sans le déchiffrer. Nous analyserons ce mécanisme en détail dans le prochain article.
• Signature électronique du bulletin crypté conformément à GOST R 34.10-2012.

Compter les totaux. Au stade de la synthèse, ce qui suit est effectué:

• Ajout homomorphe de bulletins de vote cryptés.
• Décryptage partiel préliminaire du bulletin de vote résumé final par des parties de la clé privée par les participants contrôlant les nœuds individuels et les serveurs de comptage avec la réception des textes chiffrés de chaque participant;
• Assemblage de la clé privée dans la Commission électorale et décryptage partiel du bulletin final résumé avec la clé collectée.
• La somme finale des textes chiffrés et la réception des résultats de comptage.
• Génération et vérification de la preuve de connaissance zéro Chaum-Pedersen. Utilisé pour prouver l'exactitude du décryptage du bulletin final résumé. Nous analyserons ce mécanisme en détail dans le prochain article.

Audit . À ce stade, des vérifications de validation de toutes les étapes du protocole peuvent être effectuées, et dans cet article, nous examinerons de plus près les vérifications possibles.



Examinons de plus près les mécanismes cryptographiques.

Plateforme blockchain

Avant de parler de la procédure de génération de clés, vous devez donner une introduction à la mise en œuvre de la plateforme blockchain.



La figure ci-dessous montre une disposition cible simplifiée de la plate-forme blockchain.







Le placement et la réservation des nœuds blockchain ont lieu dans des centres de données géographiquement répartis de PJSC Rostelecom. Dans ce cas, la responsabilité de l'ensemble «atomique» des composants impliqués dans le stockage de toutes les données de vote peut être attribuée à la commission électorale ou à diverses institutions d'observation publique.



Ceci est fait afin de fournir aux participants la possibilité de contrôler les principaux composants du système et des nœuds du réseau, et en même temps de ne pas traiter les problèmes de sécurité de l'information, de déploiement et d'exploitation des moyens techniques, ainsi que d'assurer l'évolutivité du système.



La liste des participants peut changer au fil du temps - d'une liste minimale au stade du lancement du système en exploitation commerciale, à une liste assez large et complètement décentralisée à mesure que le système se développe. Dans ce cas, il est toujours possible de placer un ensemble de composants en dehors du centre de données.



La solution domestique Waves Enterprise est utilisée comme plateforme blockchain. Les transactions et les blocs sont signés conformément à GOST R 34.10-2012.

Générer des clés de chiffrement

La clé publique pour le cryptage des bulletins de vote est générée à l'aide de deux algorithmes cryptographiques: le DKG Pedersen 91 Distributed Key Generation Protocol et le Shamir Key Sharing Protocol. Sur la base de chacun de ces algorithmes, une clé publique «intermédiaire» est générée. Ensuite, ces deux clés sont combinées en une clé commune.



Le schéma d'assemblage des clés est illustré ci-dessous dans la figure.







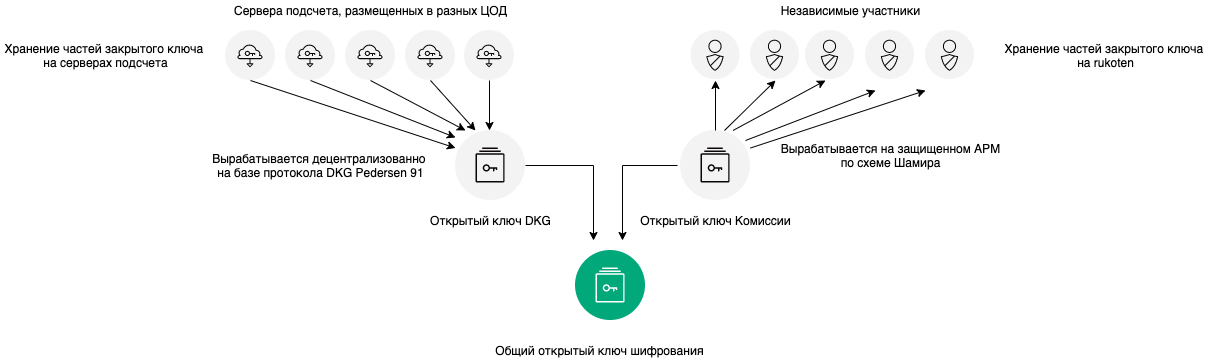
En général, un tel système peut sembler redondant, mais c'est ainsi que nous pouvons obtenir une confidentialité maximale du vote avant qu'il ne se termine. Cela est dû au fait que la clé privée générée à l'aide du protocole DKG n'est jamais au même endroit dans la forme assemblée et ne peut pas être volée de manière malveillante avant ou après la génération, et ses parties sont détenues par des parties indépendantes qui interagissent les unes avec les autres uniquement via la blockchain.



Mais si vous ne pouvez pas assembler un quorum de participants indépendants, la routine blokcheyn-network commence à séparer la clé entre les parties indépendantes, qui sont les gardiens des parties individuelles de la clé à enregistrer sur un support externe (la clé de la Commission), la



procédure de cryptage à clé publique commune commence à la veille du vote, rendant la procédure ouverte à la Commission la clé... À un certain moment avant le début du vote, en présence d'observateurs et de journalistes sur un ordinateur portable sécurisé non connecté au réseau local ou à Internet, à l'aide d'un utilitaire spécial, une paire de clés est générée, suivie de la division de la clé privée en n1 parties et de leur enregistrement sur un support spécial. La commission électorale, par sa décision, détermine les porteurs des parties de la clé privée. Au stade de la création et de l'initialisation d'un vote, la clé publique de la commission sera enregistrée dans la blockchain.



Ensuite, la création du vote dans le réseau blockchain est initiée. Après avoir créé un vote sur les serveurs de comptage, la procédure de génération de la clé publique DKG est automatiquement lancée .



Les participants à la procédure de génération de clé distribuée sont n serveurs de comptage des votes, dont nous avons parlé plus tôt dans l' article de synthèse . Toutes les opérations d'interaction entre les serveurs de comptage, intermédiaires et finaux, sont enregistrées dans la blockchain, et sont donc transparentes et vérifiables. Le système implémente le schéma de seuil "k sur n", c'est-à-dire que lors du décryptage des données, la participation de toutes les n parties qui ont formé la clé publique DKG n'est pas requise, un plus petit nombre de participants k est suffisant. Cela permet le déchiffrement des résultats de vote même si les serveurs de comptage nk ne sont pas disponibles ou si leurs clés privées ont été perdues.



Pour générer la clé publique, on utilise l'algorithme DKG (Distributed Key Generation), décrit dans l'article «Un cryptosystème à seuil sans tiers de confiance» de Torben Pryds Pedersen, transféré sur des courbes elliptiques. On suppose que chaque serveur a une paire de clés constante (enregistrée par le registraire dans le compte) Diffie-Hellman utilisée pour la transmission sécurisée des données vers ce serveur (exportation / importation des partages de clés).

Paramètres de protocole

• Une courbe elliptique E et un générateur P d'un sous - groupe de cette courbe d'ordre premier q grand. L'implémentation actuelle utilise la courbe secp256k1 .
• Un autre générateur Q du même sous-groupe dont la valeur $$ inconnu de personne.$x: Q=x⋅P$
• (k, n), où n est le nombre total de participants qui ont généré des paires de clés, et k est le nombre minimum de participants nécessaire pour restaurer le secret partagé, tandis que $$ . Autrement dit, si lesparticipantsk-1sont compromis ou si leurs clés sont volées, cela n'affectera en aucune façon la sécurité du secret partagé.$k≤(n+1)/2$

En général, l'algorithme pour obtenir le point Q est le suivant: n'importe quelle séquence d'octets est prise, par exemple la chaîne "Hello, World!", Et le hachage h = Hash ("Hello, World!") Est calculé à partir de celui-ci, après quoi nous convertissons la séquence d'octets h en un nombre et considérer $$ , où p est le module de la courbe, on substitue$x0=h mod p$$$ dans l'équation de la courbe:$x0$$$ et essayez de le résoudre pour y. En l'absence de solution, nous incrémentons x0 et essayons à nouveau de résoudre l'équation pour une nouvelle valeur de x0, etc. Étape 0. Chacun des n serveurs se voit attribuer un numéro de séquence unique de 1 à n. Ceci est nécessaire car le coefficient de Lagrange dépend du numéro de série du serveur. Étape 1 - Création d'une clé publique DKG. Chaque j -ème serveur, j = 1, ..., n: 1. Génère une paire de clé privée 〖priv〗 _j et une clé publique$y^2= x0^3+ a*x0+b mod p$















$$ 2. Prend un engagement Pedersen pour la clé publique: Génère un nombre aléatoire r_j Calcule un point$Pub_j=priv_j⋅P.$





$$$C_j=r_j⋅Q+Pub_j$

$$ publié à l'aide du compteur 3. Une fois que tous les serveurs ont publié leurs valeurs C_i, le scalaire r_j est publié. En utilisant des scalaires, n'importe qui peut récupérer les clés publiques de chaque serveur$C_j$





$$ et calculer la clé publique DKG$Pub_j=C_j-r_j⋅Q$$$ . La clé publique DKG est écrite dans la blockchain. Étape 2 - Générer des polynômes et distribuer les ombres. Chaque j -ème serveur, j = 1,…, n: 1. Génère un polynôme aléatoire de degré k-1:$Pub=∑_(j=1)^n Pub_j$















$$ où le coefficient$f_j (x)=f_(j,0)+f_(j,1)⋅x+⋯+f_(j,k-1)⋅x^(k-1),$

$$ , et le reste sont des éléments aléatoires du champ GF (q). 2. Compte les valeurs du polynôme$f_(j,0)=priv_j$



$$ 3. Crypte la valeur$f_j (i),i=1,…,n,i≠j.$



$$ utilisant la clé publique d'exportation / importation du i-ème serveur pour chaque i et publie les résultats de chiffrement à l'aide du compteur. Étape 3 - vérification des coefficients des polynômes. Chaque j -ème serveur, j = 1, ..., n: 1. Publie chaque coefficient de son polynôme multiplié par le générateur P.$f_j (i)$













$$ 2. Décode toutes les valeurs$F_(j,0)=f_(j,0)⋅P,F_(j,1)=f_(j,1)⋅P,…,F_(j,k-1)=f_(j,k-1)⋅P$

$$$f_i (j),i=1,..,n,i≠j$ et vérifie leur exactitude:

Calcule$$ Calcule la somme Si A = B, alors le résultat est accepté, sinon une plainte est publiée contre le serveur i, et le protocole est lancé depuis le tout début - passez à l'étape 0. 3. Si personne n'a de plaintes, alors il calcule propre clé privée La clé publique DKG peut être récupérée et vérifiée à partir des données enregistrées par les serveurs de comptage dans la blockchain au stade du lancement du vote. Il est nécessaire de prendre les points de clé publique de tous les déchiffrages et de les ajouter. Le résultat sera la même valeur enregistrée dans la blockchain que la clé publique DKG.$A=f_i (j)⋅P$

















En outre, sur la base de la clé publique de la commission, qui est chargée dans le système, et des clés publiques des serveurs de comptage, une clé de chiffrement publique commune est générée selon la formule suivante:



MainPubKey = Hash (PubDKG, PubCommission) * PubDKG + Hash (PubCommission, PubDKG) * PubCommission



Toutes les clés publiques sont enregistrées dans blockchain ainsi que des calculs intermédiaires pour faciliter la vérification par les observateurs. La clé de chiffrement publique partagée est lue à partir de la blockchain et transmise aux appareils des utilisateurs lorsque la newsletter est affichée.

Description du schéma de chiffrement des bulletins

Vous trouverez ci-dessous une description de la procédure de cryptage des bulletins de vote en utilisant le schéma El-Gamal sur des courbes elliptiques.



Le schéma de cryptage El Gamal sur courbes elliptiques permet de mettre en œuvre un cryptage homomorphe par rapport à l'addition, dans lequel, suite à l'opération d'addition sur le texte chiffré, une somme cryptée des valeurs originales est obtenue.



Chiffré (A) + Chiffré (B) = Chiffré (A + B).



Pour utiliser cette propriété de l'algorithme, le bulletin de vote électronique terminé est représenté par une chaîne de zéros et de uns. Le nombre de caractères correspond au nombre de choix, tandis que celui sélectionné est représenté par un, les autres choix sont représentés par des zéros.



La longueur de la clé privée lors de l'utilisation de l'algorithme ElGamal sur des courbes elliptiques est sélectionnée pour être de 256 bits, tandis que la clé publique est un point sur la courbe elliptique. Cela correspond à un niveau de sécurité de 128 bits (2 ^ 128 opérations de points de courbe sont nécessaires pour craquer). Ce niveau est considéré comme optimal pour la plupart des systèmes industriels et financiers modernes, y compris la norme russe GOST 34.10-2018 «Technologie de l'information. Protection des informations cryptographiques. Processus de formation et de vérification des signatures numériques électroniques "(version 256 bits).



Secp256k1 est utilisé comme courbe elliptique.



Disons que nous avons une paire de clés priv, Pub:

Number priv: 0 <priv <q

Point Pub = priv *



Chiffrement de base :

• Il y a un message m, un petit nombre que nous voulons crypter sur la clé Pub.
• Calculer le point M = m * Base
• Générer un nombre aléatoire r: 0 <r <q
• Calculer le point R = r * Base et le point C = M + r * Pub
• Texte chiffré: (R, C)

Décryptage:

• Possède une clé privée privée et un texte chiffré (R, C)
• Calculer le point M = C - priv * Base
• Reconstruction de m: résolution par ECDLP en force brute pour le rapport M = m * Base

Homomorphisme du schéma.



On voit que si on crypte deux messages$$$M1 = m1*Base$ et $$$M2 = m2*Base$ sur la clé Pub:

$$$(R1, C1) = (r1*Base, M1 + r1*Pub)$

$$$(R2, C2) = (r2*Base, M2 + r2*Pub)$



Puis leur somme $$$(R1 + R2, C1 + C2)$ correspond au message chiffré $$$M1 + M2$...



Ainsi, tous les bulletins de vote peuvent être cryptés et pliés «candidat par candidat». Par exemple, laissez un bulletin ouvert ressembler à ceci:



Ivanov Petrov Sidorov



0 1 0



Ensuite, en le transformant en points, nous obtenons:



Ivanov Petrov Sidorov



ZeroPoint Base ZeroPoint



où ZeroPoint est un point à l'infini.



Et enfin, nous chiffrons la newsletter sur la clé Pub:



Ivanov Petrov Sidorov



$$$(r1*Base, r1*Pub)$ $$$(r2*Base, Base + r2*Pub)$ $$$(r3*Base, r3*Pub)$



Disons que nous avons mené un tel vote avec N électeurs. Si pour Ivanov, Petrov et Sidorov, nous ajoutons séparément les textes chiffrés de différents bulletins de vote, nous obtenons un bulletin de vote sommaire, qui contient des montants chiffrés pour chacun des candidats. Ce bulletin de vote sommaire peut être décrypté avec une clé de décryptage et les résultats du vote pour chacun des candidats peuvent être trouvés.



La figure ci-dessous montre un schéma d'empilement et de validation homomorphique des bulletins de vote basé sur des preuves de connaissance zéro.







Comme nous pouvons le voir sur le diagramme, un attaquant potentiel n'a aucun moyen de "lancer" des votes supplémentaires en chiffrant un nombre incorrect au niveau du protocole cryptographique. Ceci est accompli en utilisant des preuves de connaissance zéro, qui seront abordées plus loin dans l'article. De plus, les vérifications nécessaires sont également implémentées dans l'application Web de l'électeur.

Description de la procédure de décryptage

Les votes sont comptés sans décryptage grâce au cryptage homomorphe selon le schéma El-Gamal, qui permet de maintenir la confidentialité de l'ensemble de la procédure de vote et de chaque vote individuel. De plus, aucun des serveurs n'a la capacité de décrypter indépendamment et secrètement les résultats du vote.



Afin de décrypter le texte chiffré (R, C), il est nécessaire que tout k serveur sur n calcule et publie la valeur$$$s_j⋅R$ et la preuve de l'exactitude du décryptage de Chaum-Pedersen (preuve que le $$$s_j⋅R$ Est précisément le point R multiplié par $$$s_j$sans révéler le sens $$$s_j$). En outre, pour cela, il est nécessaire de collecter la clé privée de la commission d'au moins k1 à partir de t1 parties et avec son aide également d'effectuer le calcul$$$s_j⋅R$avec publication dans la blockchain.







Le décryptage se déroule en plusieurs étapes, dont les résultats sont enregistrés dans la blockchain.



Premier pas- décryptage partiel. Chaque K des N serveurs du système additionne les textes chiffrés des votes, reçoit un bulletin de vote sommaire et déchiffre la clé de vote privée de sa part. Le résultat de cette opération sera un texte chiffré, dont la combinaison avec les textes chiffrés obtenus à la suite des mêmes opérations effectuées sur les autres serveurs de comptage, ainsi qu'avec le texte chiffré reçu sur la clé privée de la commission, donnera un résultat final déchiffré. Il est important de noter que s'il n'y a pas de texte chiffré obtenu à partir du décryptage sur la clé privée de la commission, tous les autres textes chiffrés deviennent inutiles. Il est impossible d'en obtenir des résultats.



Les résultats de l'opération sont publiés sur la blockchain.



Seconde phase- assemblage de la clé privée de la commission et décryptage partiel du scrutin sommaire. Cette opération est effectuée sur un PC spécial sans connexion Internet. Une fois la clé collectée, l'opération décrite dans le paragraphe précédent a lieu pour former le texte chiffré sur la clé de commission. Les résultats de cette opération sont également enregistrés dans la blockchain.



La troisième étape est le décodage final. Les serveurs de comptage des votes agrègent les résultats K de N serveurs, le résultat du décryptage sur la clé privée de la commission, et produisent le décryptage final, puis publient les résultats du vote.



Veuillez noter que la présence du texte chiffré généré sur la clé privée de la commission est un prérequis. Sans cela, le calcul des résultats n'aura pas lieu.



Sur la base des résultats publiés du décryptage partiel, toute partie intéressée peut répéter le processus et vérifier que les résultats sont correctement comptés.

Preuve de connaissance zéro

Bien que le système DEG soit protégé contre les intrus et les erreurs des utilisateurs au niveau du logiciel et de l'infrastructure, des preuves et des vérifications mathématiques supplémentaires ont été fournies au niveau du protocole cryptographique, qui ne permettent pas de transférer de fausses informations vers le système. Pour cela, plusieurs mécanismes ont été développés sur la base de la preuve non interactive de connaissance zéro (NIZK).



Le premier type de ZKP (zero-knowledge proof) appliqué dans le système est la preuve de plage. Les données du ZKP sont utilisées lors de la publication d'un bulletin de vote crypté de sorte qu'en l'absence d'informations sur la façon dont l'électeur a voté, il serait possible de s'assurer que l'électeur n'a pas gâché le bulletin de vote sur son appareil de l'une des manières suivantes:

• le participant n'a pas chiffré une valeur supérieure à un dans le bulletin de vote pour une option de vote distincte, ce qui aurait une incidence sur le résultat du vote en cas d '«ajout chiffré»;
• le participant n'a pas choisi plus d'une option pour chaque question du bulletin de vote, sauf si cela est prévu par la procédure de remplissage du bulletin de vote.

Une description plus détaillée de l'implémentation de NIZK, ainsi que leur vérification, seront discutées dans un article séparé.

Structure des enregistrements dans la blockchain

Toutes les informations de la blockchain sont enregistrées par trois types de transactions:

• CreateContract - pour créer un contrat intelligent pour un vote spécifique. De plus, dans ce contrat intelligent, toutes les informations sur le vote seront regroupées. Si deux (ou plus) votes ont lieu simultanément, alors deux (ou plus) copies du contrat sont respectivement créées.
• CallContract - pour interagir avec un contrat intelligent pour diverses opérations, dont une liste est donnée ci-dessous.
• Transaction de données - pour enregistrer la liste électorale après avoir créé une instance du contrat intelligent de vote et avant de commencer le vote lui-même.

L'interaction avec un contrat intelligent est réalisée par les opérations suivantes:

• Écrire des données de base dans un contrat intelligent. Les clés publiques des serveurs de comptage qui participeront au protocole cryptographique, le schéma de seuil, les clés de vérification de signature aveugle et d'autres données nécessaires à l'organisation du protocole et au vote en général sont stockées ici.
• dkgScalar, dkgCommit, dkgShadows - données requises pour créer une clé publique pour le cryptage des bulletins de vote et implémenter un seuil k de n schémas. Nous en reparlerons plus tard dans l'article.
• addMainKey – .
• blindSigIssue – .
• vote – .
• finishVoting – . .
• Decryption – . .
• ComissionDecryption – .
• Results – . , .

Une transaction de vote d'électeur comprend l'adresse blockchain et la clé publique d'un électeur, un bulletin de vote crypté, une signature aveugle et une signature électronique générée sur la clé privée anonyme de l'électeur (voir l'article publié précédemment sur l'anonymisation).



Les figures ci-dessous montrent l'affichage d'une transaction avec une voix dans le client blockchain.











Toutes les informations sur le vote sont agrégées sur un contrat intelligent et seront disponibles via le client blockchain aux observateurs ou sous la forme d'un fichier csv à n'importe qui.



La figure ci-dessous montre l'affichage des informations agrégées dans un contrat intelligent.





* Données du serveur de test.



Les fonctionnalités de la plate-forme Waves Enterprise vous permettent de mettre en œuvre une logique assez complexe avec un modèle de statut, une vérification de signature aveugle et le comptage des bulletins valides et annulés.

Vérification du protocole cryptographique et du processus de vote

Le premier contrôle de base qui peut être effectué à l'aide de la plateforme blockchain et du client blockchain est de vérifier si le nombre d'électeurs sur la liste électorale correspond au nombre de bulletins émis et au nombre de votes enregistrés.



Le contrôle de l'exactitude du dépouillement est effectué en répétant le travail du serveur de dépouillement par l'observateur pour résumer les bulletins de vote chiffrés candidat par candidat. Cela se fait en ajoutant séquentiellement les points de la courbe elliptique correspondant à chaque candidat.



Ensuite, à l'aide du bulletin récapitulatif crypté reçu et de la preuve du décryptage correct, qui sont publiés sur la blockchain, il est possible de vérifier l'exactitude de la sommation et du décryptage partiel effectués par chaque serveur de comptage.



À ce stade, vous pouvez voir si le montant chiffré reçu par l'observateur correspond à ce que chacun des serveurs de comptage a enregistré.



Après cela, vous pouvez vérifier l'exactitude du décryptage des résultats du vote. Pour ce faire, vous devez prendre des textes chiffrés des transactions avec le type d'opérations Décryptage et CommissionDécryptage et, par analogie avec les bulletins de vote, ajouter les points de la courbe elliptique pour chaque candidat.



Le code source des opérations cryptographiques est disponible dans ce référentiel GitHub.