Faire des décisions. Exemple

Poursuivant le sujet, je dirai que j'ai regardé les publications d'autres auteurs Habr sur ce sujet. Il y a de l'intérêt pour les problèmes, mais personne ne veut entrer dans la théorie. Agissant comme des découvreurs pionniers. Ce serait formidable s'ils reçoivent de nouveaux résultats, de nouvelles réalisations, mais personne ne s'y efforce.



Mais en fait, cela s'avère pire que ce que l'on sait déjà, beaucoup de facteurs ne sont pas pris en compte, les résultats de la théorie sont appliqués là où elle ne le recommande pas et en général, tout n'a pas l'air très sérieux, bien que Habr, comme il faut le comprendre, ne s'efforce pas pour cela. Les lecteurs ne peuvent et ne doivent pas agir comme un filtre.

L'ensemble original d'alternatives, leur mesure et leur évaluation

On sait que les problèmes de recherche d'une solution ne se posent que dans des situations de choix multi-alternatives. Pour considérer la situation de prise de décision, formuler un problème de prise de décision (DP) spécifique, choisir une méthode pour le résoudre, il est nécessaire d'avoir des informations initiales sur les alternatives, une relation de préférence.



Montrons dans la sous-section quelles sont les méthodes pour l'obtenir. Les alternatives ont de nombreuses propriétés (caractéristiques) qui influencent la décision. Par exemple, les indicateurs des propriétés des objets (poids, volume, dureté, température, etc.) peuvent être quantitatifs ou qualitatifs.



Soit une propriété de l'ensemble des alternatives de Ω exprimée par un nombre, c'est-à-dire qu'il existe une application ψ: Ω → E1, où E1 est l'ensemble des nombres réels. Ensuite, une telle propriété est caractérisée par un indicateur, et le nombre z = ψ (x) est appelé la valeur (estimation) de l'alternative en termes d'indicateur.



Pour évaluer les alternatives, il est nécessaire de mesurer les indicateurs.



Définition. La mesure d'un indicateur d'une certaine propriété s'entend comme l'attribution de valeurs numériques à des niveaux individuels de cet indicateur dans certaines unités. Dans ce cas, le choix de l'unité de mesure est important.



Ainsi, par exemple, si le volume d'une certaine partie du conteneur est d'abord mesuré en mètres cubes puis en litres, alors l'essence de l'indicateur ne changera pas; seul le nombre d'unités changera. Ces métriques de propriété peuvent être mises à l'échelle, multipliées ou divisées par une valeur constante pour la métrique de propriété.



Par contre, il existe des propriétés dont les indicateurs ne permettent pas une telle manipulation de leurs valeurs. Le degré d'échauffement des corps est caractérisé par la température et est mesuré en degrés. La valeur de cet indicateur + 10 ° et –15 ° ne permet pas de juger combien de fois le corps avec une température de + 10 ° est chauffé plus qu'un corps avec une température de -15 °



A partir de ces exemples, il est possible (et important) de conclure que les indices volume et température se réfèrent à différents types de propriétés, sur les valeurs de z = ψ (x) dont certaines transformations f (z) = f (ψ (x)) ...



A savoir, l'ensemble des transformations admissibles f (z) est pris comme base pour déterminer le type d'échelle dans laquelle l'indicateur d'un certain attribut (propriété) est mesuré. En effectuant l'une ou l'autre mesure de l'indicateur d'une caractéristique mise en évidence par le chercheur, nous arrivons à la tâche de déterminer le type d'échelle dans laquelle la mesure doit être effectuée.



Sans résoudre correctement ce problème, on peut admettre une mauvaise manipulation des résultats des observations (mesures) lors de leur traitement. Cela se produit lorsque les valeurs des indicateurs sont soumises à des transformations prises en dehors de l'ensemble des transformations autorisées pour un type d'échelle donné.



Définition. Une échelle de mesure est une séquence de valeurs du même nom de différentes tailles acceptées d'un commun accord.

Examinons plus en détail les principaux types d'échelles.







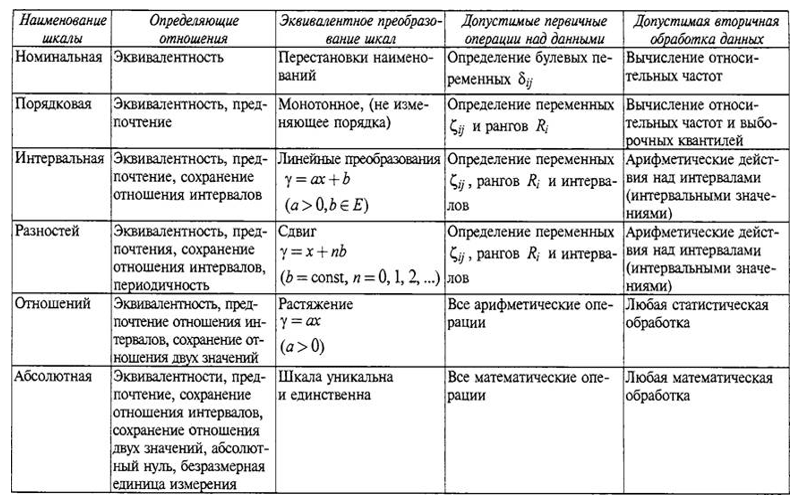
1. Échelles nominales . Des échelles nominales sont utilisées lorsqu'un chercheur traite des objets décrits par certaines caractéristiques. Selon qu'un objet donné a une certaine valeur d'une caractéristique ou son absence, l'objet est référencé à l'une ou l'autre classe.



Par exemple, si nous parlons de personnes, alors la valeur de la caractéristique (l'échelle de la caractéristique est formée par deux valeurs de sexe: masculin et féminin) permet d'assigner sans ambiguïté chaque personne à une certaine classe. Pour cette raison, l'échelle est appelée l'échelle de notation. Un tel signe en tant que profession permet à une personne d'être appelée, par exemple, un enseignant, un charpentier ou autrement en fonction de la valeur de l'indicateur de la profession.



L'échelle dans ce cas est formée par les noms de toutes les professions. Evidemment, zéro n'est pas indiqué sur cette échelle, bien que l'absence de profession dans le sujet lui permette de se classer précisément dans la catégorie des personnes sans profession. Les noms des professions ne sont en aucun cas classés sur cette échelle, bien qu'ils soient souvent classés par ordre alphabétique pour des raisons de commodité.



À partir de ces considérations, une telle échelle est appelée échelle de dénomination.

Les transformations valides des valeurs dans cette échelle sont toutes des fonctions un-à-un: f (x) ≠ f (y) <=> x ≠ y.



2. Échelles ordinales . Si le trait étudié, par exemple, la dureté du matériau, se manifeste différemment dans les objets et a des valeurs qui ne peuvent pas être spécifiquement mesurées, mais que l'on peut juger sans équivoque l'intensité comparative de sa manifestation pour deux objets quelconques, alors ils disent que la valeur du trait est mesurée sur une échelle ordinale. Un exemple classique de ceci est la dureté des minéraux. Le point de référence est 0 sur l'échelle n'est pas défini.



La valeur caractéristique est définie comme suit. Le minéral plus dur de la paire en question laisse une égratignure sur l'autre. Tous les minéraux en fonction des valeurs de ce trait peuvent être classés comme suit: le premier est le moins dur, le second est plus dur, il ne laisse une égratignure que sur le premier, le troisième laisse une égratignure sur les deux premiers, etc.



La différence entre l'échelle ordinale et la nominale est que les valeurs du trait peuvent être triées, tandis que les valeurs sur l'échelle nominale ne peuvent même pas être commandées. L'inconvénient d'une échelle ordinale est qu'elle n'est pas proportionnelle.



Il est impossible de répondre à la question de savoir combien ou combien de fois un minéral est plus dur qu'un autre. Les transformations admissibles de l'échelle ordinale sont constituées de toutes les fonctions monotones croissantes de propriété: x ≥ y => f (x) ≥ f (y).



3.Échelle d' intervalle (intervalle). diffèrent des échelles d'ordre en ce que, pour les propriétés qu'elles décrivent, il a un sens non seulement les relations d'équivalence et d'ordre, mais aussi la sommation des intervalles (différences) entre diverses manifestations quantitatives de propriétés. Un exemple typique est l'échelle d'intervalle de temps.



Des intervalles de temps (par exemple, des périodes de travail, des périodes d'études) peuvent être ajoutés et soustraits, mais l'ajout des dates de tout événement n'a pas de sens.



Un autre exemple, l'échelle des longueurs (distances) - les intervalles spatiaux est déterminé en alignant le zéro de la règle avec un point, et la lecture est effectuée à un autre point. Ce type d'échelle comprend également les échelles de température Celsius, Fahrenheit, Reaumur.



Les transformations linéaires sont admises dans ces échelles, (x - y) / (z -v); x ∓ y; ils appliquent des procédures pour trouver l'espérance mathématique, l'écart type, le coefficient d'asymétrie et les moments décalés.



4. Échelle des différences (point) Les échelles des différences diffèrent des échelles d'ordre en ce que l'échelle des intervalles peut déjà être jugée non seulement que la taille est plus grande qu'une autre, mais aussi combien plus, en substance, il s'agit de la même échelle absolue, mais ses valeurs sont décalées de une valeur relative aux valeurs absolues (x - y) <(z -v); x ∓ y;



5. Échelle des relations... L'échelle pour laquelle l'ensemble des transformations admissibles comprend toutes les transformations de similarité est appelée l'échelle des relations. Le point de référence est fixé sur cette échelle et l'échelle de mesure peut être modifiée pour cela.



Laissez cette échelle mesurer la longueur d'un objet. Dans ce cas, vous pouvez passer de la mesure en mètres à la mesure en centimètres, en diminuant l'unité de mesure d'un facteur 100. Evidemment, dans ce cas, le rapport des longueurs L (A) et L (B) de deux objets A et B, mesurés dans les mêmes unités, ne changera pas lorsque les unités seront modifiées.



Les valeurs de l'indicateur du trait, mesurées dans cette échelle, permettent de

répondre à la question de savoir combien de fois plus intensément le trait se manifeste dans un objet que dans un autre. Pour cela, il faut considérer le rapport des valeurs L (A) / L (B) = k.



Si le rapport est supérieur à un (k> 1), la valeur de l'indicateur d'attribut pour le premier objet A est k fois supérieure à celle de B, si k <1, alors la valeur de l'indicateur d'attribut pour l'objet B est 1 / k fois supérieure à celle de A. est la multiplication par un entier positif et seulement cela.



6. Échelle absolue . La plus simple de toutes les échelles est une échelle qui permet une seule transformation f (x) = x. Cette situation correspond à la seule façon de mesurer l'indicateur de la propriété d'un objet, à savoir un simple recomptage d'objets.



Cette échelle est appelée l'échelle absolue. Lorsque nous enregistrons l'objet x, nous ne sommes intéressés par rien d'autre que cet objet. L'échelle absolue peut être considérée comme une implémentation particulière de certaines autres échelles.

Tâche décisionnelle. Obtenir une matrice de relations

Nous listons les paramètres possibles du ZPR, notamment:

• ordre linéaire des alternatives (le sommet de la chaîne est le meilleur);
• mettre en évidence la meilleure alternative;
• mettre en évidence un sous-ensemble (non ordonné) des meilleures alternatives;
• mettre en évidence un sous-ensemble ordonné des meilleures alternatives;
• commande partielle des alternatives;
• division ordonnée (partiellement ordonnée) des alternatives;
• partitionnement non ordonné des alternatives (classification).

Sur la base de l'analyse des mesures des indicateurs des propriétés des alternatives à différentes échelles, les résultats de mesure peuvent être présentés de différentes manières [1, 5].



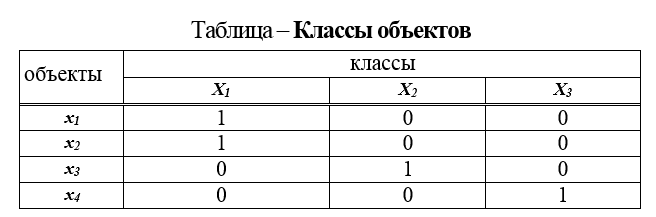
1. Tableau de classification. Le tableau est obtenu lorsque les mesures sont prises à des échelles nominales et est un tableau dont les lignes sont: le nom de l'objet, et les colonnes sont les noms des classes$$$X_1, X_2, X_3,$ ... etc. Dans les colonnes classe 1, classe 2, etc., 1 est mis si l'objet appartient à cette classe et 0 - sinon (Table Classes of objects).



Dans la table de classe, les objets $$$x_1 ,x_2 є X_1, x_3 є X_2, x_4 є X_3.$



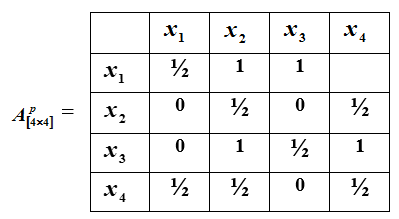
2. Matrice de la relation des préférences. Obtenu en prenant des mesures dans des échelles ordinales. Révéler les préférences sur l'ensemble des objets Ω signifie indiquer l'ensemble de toutes ces paires d'objets (x, y) de cet ensemble pour lesquelles l'objet x est préférable (par exemple, plus dur) que l'objet y. La matrice des relations de préférence est obtenue comme suit. (voir ici, fig 2.15)



En construction$$$_{[n×n]}^p$ matrice carrée. Sa i-ème ligne correspond au i-ème élément$$$x_i$ ensemble Ω, et la jième colonne à l'élément$$$x_j$ . A l'intersection de la i-ème ligne et de la j-ème colonne, 1 est mis si l'objet$$$x_i$ préféré à l'objet$$$x_j$ , zéro si l'objet$$$x_j$ préféré à l'objet$$$x_i$ , 1/2 si objets$$$x_i$ et$$$x_j$ indifférents, et rien n'est mis - si les objets sont incomparables$$$x_i$ et$$$x_j$ ne peut pas être comparé.



Un exemple d'une telle relation de préférence est présenté dans la matrice ci-dessous.





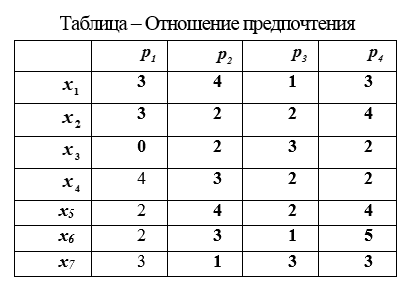
3. Tableau des indicateurs. Obtenu lors de la mesure dans l'échelle des relations. Les propriétés des indicateurs qui seront mesurés sont sélectionnées. La mesure de ces propriétés est effectuée et les résultats de mesure sont enregistrés dans un tableau.



En colonnes$$$p_1, p_2, p_3, p_4$ tableaux Le rapport de préférence contient les valeurs des indicateurs de propriété par lesquels les objets sont évalués$$$x_1,x_2,x_3,x_4,x_5,x_6$ et$$$x_7$ .



Après avoir reçu les résultats de mesure dans ces formes de présentation, nous devons afficher les résultats sous forme de relations, car nous allons résoudre le ZPR, en nous appuyant sur l'appareil bien développé de la théorie des relations binaires.



Le mappage de la table de préférences à la matrice de relations binaires est le suivant:





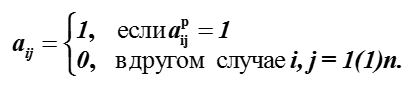
À partir de la matrice des relations de préférence $$$_{[4×4]}^p$ pour 4 alternatives présentées dans le tableau. La relation de préférence sera la matrice$$$_{[4×4]}^p$ , qui ressemble à ceci:





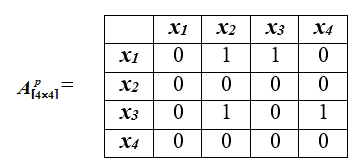
Le mappage de la carte de score à la matrice du ratio de préférence est le suivant: $$$a_{i,j}=1$ si:

1) le nombre d'indicateurs par lesquels l'objet$$$x_i$ préféré à l'objet$$$x_j$ supérieur au nombre d'indicateurs par lesquels l'objet$$$x_j$ préféré à l'objet$$$x_i$ ;



2) pour l'objet$$$x_i$ aucun des indicateurs ne prend la plus petite valeur possible.



3) la condition 1 implique que les indicateurs pour lesquels l'objet$$$x_i$ pas pire que l'objet$$$x_j$ , constituent la majorité de tous les indicateurs considérés.



Cependant, si cette condition est remplie, il se peut que selon les indicateurs pour lesquels l'objet$$$x_i$ pire que l'objet$$$x_j$ , la différence est significative; Pour réduire le nombre de ces cas en donnant la préférence à x, la condition 2 est introduite.

Méthodes pour résoudre le problème de la prise de décision

Soit, après avoir reçu les données initiales, la relation R sur l'ensemble des alternatives $$$Ω= {(x_1, ...,x_n)}$... Et la tâche est de prendre une décision. La méthode principale est un ordre linéaire (classement) des alternatives, c'est-à-dire aligner les alternatives dans une chaîne par ordre décroissant de leur valeur, pertinence, importance, etc., du «meilleur» au «pire».



Le rapport R peut être:

1. attitude non transitive complète;
2. une relation d'ordre partiel;
3. ordre linéaire.

Seulement dans le cas de la linéarité de la relation R, la structure des préférences répond à la tâche. Dans ce cas, le classement des alternatives à partir de l'ensemble Ω est obtenu directement en construisant un diagramme linéaire de l'ensemble ordonné. Dans le diagramme, l'alternative$$$x_i$, sera strictement supérieur à l'alternative $$$x_j$si vous préférez.



La solution du problème posé pour les relations complètes et transitives est réalisée à l'aide de méthodes (algorithme) de classement des alternatives, et pour les ordres partiels à l'aide d'un algorithme de réordonnancement linéaire. Ces algorithmes seront discutés dans les paragraphes suivants ci-dessous.



Classement des alternatives . Soit la relation [Ω, R] complète et non transitive. La propriété d'exhaustivité signifie que toutes les alternatives$$$Ω = {(x_1, ...,x_n)}$de l'ensemble sont comparables les uns aux autres. La présence de non-transitivité n'est possible que si le graphe de préférence G [Ω, R] contient des contours.



Il est nécessaire de transformer la structure du graphe de relations pour éliminer les contradictions logiques sous forme de contours. Si l'on suppose qu'il y a un contour par rapport à R$$$x_1, x_2, …,x_k, x_1,$ puis lors du classement des alternatives $$$x_1$ devrait être situé plus haut $$$x_2, x_3, …,x_k, x_1,$ce qui conduit à une contradiction.

Introduisons l'énoncé suivant [1,5].



Soit B 'et B "deux contours arbitraires d'un graphe de la forme G [Ω, R], alors si un élément$$$x_i$ є B 'domine l'élément $$$x_j$ є B '', puis n'importe quel élément $$$x_1$є B 'tout élément domine $$$x_k$є B ''.



Cette proposition permet de partitionner l'ensemble R en m sous-ensembles$$$B_1, B_2, …,B_m$tel que $$$B_i ∩ B_j=∅, ∀i,j є [1, m]; UB_i =Ω.$

Ainsi, le problème du classement des alternatives de l'ensemble se décompose en deux étapes:

1) la sélection des contours du graphe, c'est-à-dire partition de l'ensemble Ω en sous-ensembles$$$B_1, B_2, …,B_m$et l'ordre de groupe de ces sous-ensembles;

2) classement des éléments de contour sélectionnés à la première étape.



Algorithme de mise en évidence des contours d'un graphe



Pour trouver les contours d'un graphe, il existe un algorithme simple [1]. Laisser être$$$_{[n×n]}$ Est la matrice de contiguïté du graphe G [Ω, R], et $$$_{[n×n]}$–Matrice unitaire. Nous formons$$$_{[n×n]}+ _{[n×n]}$, $$$(_{[n×n]}+ _{[n×n]})^2$, $$$(_{[n×n]}+ _{[n×n]})^3$,… Une suite de degrés de matrices, dont les éléments expriment le nombre de chemins de longueur au plus 1, 2, 3… Pour une valeur m ≤ n, on obtient l'égalité suivante (une matrice stationnaire):

$$$(_{[n×n]}+ _{[n×n]})^m=(_{[n×n]}+_{[n×n]})^{m+1}$...



Il est connu de la théorie des graphes [10] qu'à chaque système de toutes les lignes identiques d'une matrice "stationnaire" correspond un sous-ensemble des sommets du graphe se trouvant dans un contour. En regroupant les sommets correspondants en classes, on obtient une partition de l'ensemble original Ω en sous-ensembles$$$B_1, B_2, …,B_m$...



Évidemment, parmi ces sous-ensembles, on peut trouver un tel sous-ensemble$$$B_im$que les éléments de ce sous-ensemble ne seront dominés par aucun élément des autres sous-ensembles. Ce sous-ensemble sera considéré comme le meilleur et occupera la première place du classement par ordre décroissant de préférence.



Ensuite, nous trouvons le meilleur sous-ensemble parmi les sous-ensembles restants en utilisant le même principe et le mettons à la deuxième place. Nous

continuerons cette procédure jusqu'à ce que tous les sous-ensembles prennent leur place dans le classement.



Soit la relation de préférence R donnée sur l'ensemble Ω par la matrice$$$_{[6×6]}$...





Le graphe de relations R est représenté sur la Fig. G.





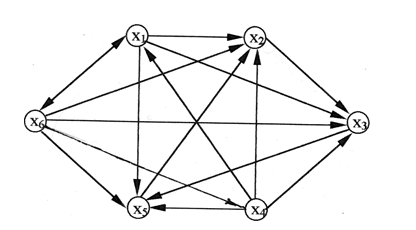
Figure: D. Graphe de relation non transitive R



Pour mettre en œuvre la première étape de classement des éléments d'un ensemble, il faut sélectionner les contours du graphe G [Ω, R]. Ceci est fait en élevant la matrice d'adjacence du graphe à des puissances successives jusqu'à ce que les matrices correspondent.



On a$$$(_{[6×6]}+ _{[6×6]})$, $$$(_{[6×6]}+ _{[6×6]})^2$, $$$(_{[6×6]}+ _{[6×6]})^3$...

Ensuite, nous calculons séquentiellement les puissances croissantes de la matrice, en les additionnant avec la matrice unitaire de la dimension correspondante jusqu'à ce que la matrice cesse de changer:





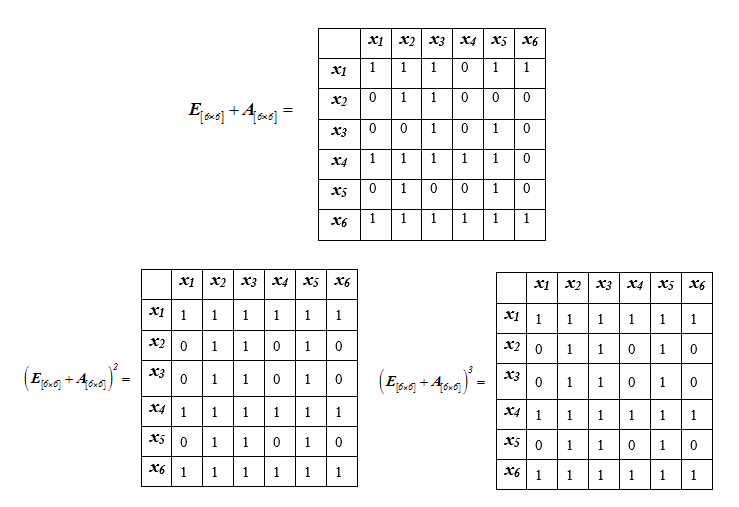
Parce que $$$(_{[6×6]}+ _{[6×6]})^2 =(_{[6×6]}+ _{[6×6]})^3$, nous pouvons conclure que $$$(_{[6×6]}+ _{[6×6]})^2 = (_{[6×6]}+ _{[6×6]})^k$, pour k ≥ 2. De l'analyse de la matrice $$$(_{[6×6]}+ _{[6×6]})^2$ il s'ensuit que les lignes correspondant aux éléments $$$x_1,x_4,x_6$coïncident, cela indique que ces éléments appartiennent au même contour du graphe G [Ω, R].



Les éléments$$$x_1,x_4,x_6$ former un ensemble $$$B_1 =(x_1,x_4,x_6)$... Un autre contour est formé d'éléments$$$x_2,x_3,x_5$qui sont inclus dans l'ensemble $$$B_2 =(x_2,x_3,x_5)$...



Ainsi, nous avons partitionné l'ensemble en m = 2 classes$$$B_1, B_2$... Réalisons un classement de groupe de ces sous-ensembles. Pour ce faire, vous devez trouver un élément$$$x_i є B_1$quel élément domine $$$x_j є B_2$...



Cela signifiera la supériorité du sous-ensemble$$$B_1$ plus de $$$B_2$... Dans notre exemple$$$x_1 є B_1$ domine $$$x_2 є B_2$... Par conséquent, le sous-ensemble$$$B_1$ domine $$$B_2$... Une représentation graphique de la dominance dans la partition Ω est représentée sur la Fig. QC.





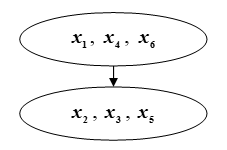
Figure: QC. Classement des contours sélectionnés à la première étape



Algorithme de classement des éléments des contours . Est-il possible de disposer les éléments d'une relation se trouvant dans le même contour, sont-ils équivalents les uns aux autres, ou y a-t-il des différences suffisamment subtiles entre eux pour les distinguer? Il s'avère qu'une telle possibilité existe en règle générale [1].



Notons par$$$B_{h_{[n×n]}}$la matrice de contiguïté du h-ème contour. Introduisons le concept$$$p^i(k)$-force d'ordre k de l'élément i, dont la valeur est calculée comme la somme des éléments de la i-ème ligne dans la matrice $$$B_{h_{[n×n]}}^k$(1).



Laisser être$$$b_{h_{[i,j]}}^k$Est l'élément de la i-ème ligne et de la j-ème colonne de la matrice, alors





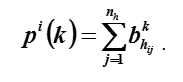
La force relative du k-ème ordre de l'élément i est comprise comme la fraction



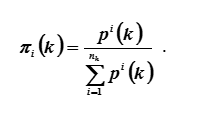
Lorsque k augmente sans bornes (k → ∞), le nombre $$$π_i(k)$tend vers une certaine limite π, que nous appellerons plus loin la force de l'élément i. Vecteur$$$_{[n]} = (π_1,...,π_n)$est appelé le vecteur limite.



En raison du théorème de Perron-Frobenius [1], la limite existe toujours. Le vecteur propre normalisé de la matrice de contiguïté coïncide avec son vecteur limite. Par conséquent, le vecteur$$$_{[n]} = (π_1,...,π_n)$(2)



peut être trouvée sans calculer les forces intégrées$$$p^i(k)$, en résolvant le système d'équations linéaires

$$$B_{h_{[n×n]}} · _{[n]} = λ_{[n]}$, (3)

où λ est la plus grande racine réelle non négative de l'équation caractéristique

$$$det(λ_{[n×n]}- B_{h_{[n×n]}}) = 0$(4)

Il est à noter que le vecteur propre normalisé d'une matrice indécomposable non négative ne change pas lorsque la matrice est multipliée par un nombre s> 0, ainsi que lorsqu'elle est additionnée avec une matrice de la forme sE.



Ensuite, les éléments de contour sont ordonnés en diminuant les valeurs des composantes vectorielles correspondantes$$$_{[n]}$, c'est à dire. l'élément i domine l'élément j quand$$$π_i >π_j$...



Nous classerons les éléments de l'ensemble$$$B_1 =(x_1,x_4,x_6)$... Construisons une matrice de préférences pour cet ensemble





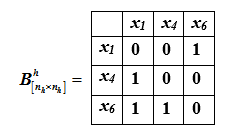
Le vecteur des forces intégrées du 1er ordre pour les éléments $$$(x_1, x_4, x_6)$ressemble à (1,1,2), le vecteur des forces relatives P (k) = (1 / 4,1 / 4,2 / 4).

Classement des articles$$$(x_1, x_4, x_6)$la force du 1er ordre est illustrée à la Fig. R.





Figure: R. Classement des éléments



Trouvons des vecteurs caractérisant les forces des 2ème, 3ème, 4ème et 5ème ordres.





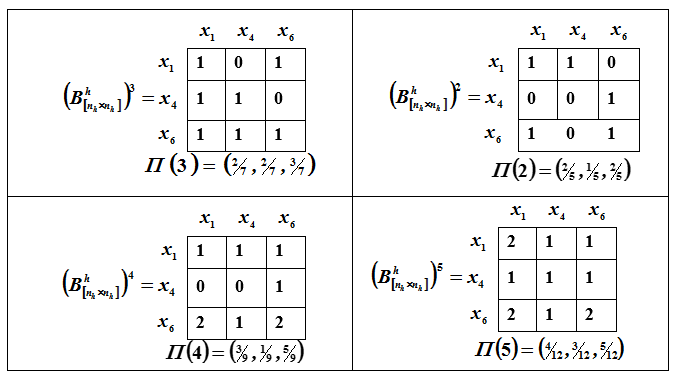
Une représentation graphique du classement est illustrée à la Fig. P.







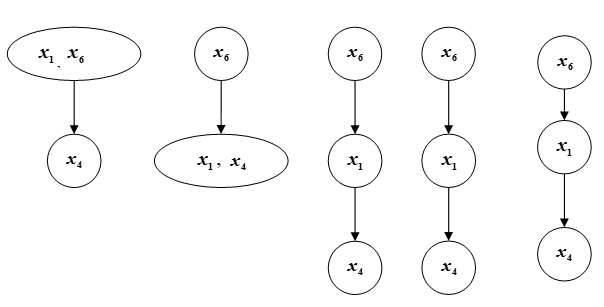
Fig. C - Chaîne



En effectuant le classement des éléments de l'ensemble B2 de manière similaire, nous obtenons les résultats représentés sur la Fig. Droite.



En combinant le classement des éléments de l'ensemble 1 et 2, nous passons à l'ordre final des éléments de l'ensemble Ω (Fig. C).

Réorganisation linéaire des commandes partielles strictes

Soit la relation R (Fig. A ci-dessous dans le texte), obtenue à la suite de l'agrégation des jugements individuels d'experts, est une relation d'ordre partiel sur l'ensemble Ω. Dans ce cas, Ω est un ensemble ordonné. La construction d'un ordre linéaire d'alternatives consiste à obtenir des évaluations globales de leurs «capacités» sur une échelle ordinale.



Pour une raison quelconque, certains experts ne peuvent pas comparer certaines paires d'alternatives en termes de préférence. Dans ce cas, la relation agrégée R sur l'ensemble Ω ne sera pas d'ordre linéaire. Evidemment, cela conduit au problème de la réorganisation linéaire des alternatives à partir de Ω. Cette réorganisation est souvent possible de plusieurs manières.



La présence de plusieurs ordres linéaires pour un ordre partiel indique que le «classement intrinsèque» dans la structure est insuffisant pour un seul ordre linéaire. Ainsi, il devient nécessaire de résoudre le problème de la réorganisation linéaire des ordres partiels. Soit R un ordre partiel.



Théorème (Spielrein [5, 10]). Tout ordre R sur un ensemble peut être étendu à un ordre linéaire sur cet ensemble.



Un corollaire du théorème de Spielrein: toute réorganisation linéaire d'un sous-ensemble$$$Ω_i ⊆ Ω$peut être étendu à une réorganisation linéaire de l'ensemble ordonné Ω.



Si X est un sous-ensemble de Ω constitué d'alternatives incomparables, alors tout ordre linéaire de X peut être étendu à un ordre linéaire de l'ensemble entier Ω. Dans ce cas, l'ordre de R est exprimé en termes d'ordres linéaires$$$R_i$...



En vertu du théorème de Spielrein, sur l'ensemble Ω il existe une numérotation$$$x_1, x_2,...,x_n$éléments de cet ensemble. La numérotation d'un ensemble ordonné à n éléments Ω, avec une relation d'ordre donné R, est une mise en correspondance un-à-un de l'ensemble Ω en lui-même, i.e. dans {1, 2, ..., n}, dans lequel l'élément «plus grand» par rapport à l'ordre correspond au plus grand nombre [5]. Dans ce qui suit, par classement des éléments, nous entendons toute réorganisation linéaire de cet ordre. Notez que la numérotation d'un ensemble ordonné représente sa dimension.



Dans le cas général, le problème de trouver des ordonnances supplémentaires linéaires est réduit à trouver toutes les numérotations admissibles de l'ensemble ordonné partiel d'origine. Vous pouvez écrire toutes les permutations d'éléments de Ω, dont il y aura n! et pour chacun, vérifiez la condition que l'élément "le plus grand" correspond au nombre le plus grand. Cependant, cette méthode de recherche de toutes les commandes supplémentaires est très laborieuse et inefficace.



Pour un ensemble ordonné Ω avec un ordre R donné, un élément x 'de l'ensemble Ω est dit maximal s'il n'y a pas d'élément x strictement plus grand, i.e. si x> x 'ne tient pas pour tout x є Ω. Un élément x '' est appelé le plus grand élément de l'ensemble ordonné [Ω, R] s'il est plus grand que tout autre élément x, c'est-à-dire pour tout x є Ω, x ''> x [5].



S'il y a un élément le plus grand dans un ensemble ordonné, alors c'est l'élément maximum. Si un ensemble ordonné a un seul élément maximum, alors ce sera le plus grand élément. Dans un ensemble partiellement ordonné, plusieurs éléments maximum sont autorisés.



Pour toute numérotation de l'ensemble de n éléments Ω, le nombre N est attribué à l'élément maximum. Toutes les numérotations de l'ensemble Ω peuvent être obtenues si toutes les numérotations de tous les sous-ensembles obtenus à partir de Ω sont connues en supprimant l'un de ces éléments maximaux. La même technique est appliquée à chaque sous-ensemble [7]. Considérons un algorithme pour construire toutes les numérotations de l'ensemble ordonné [Ω, R].



1. Un graphe auxiliaire [β, γR] de l'ensemble ordonné [Ω, R] est construit, dont les sommets satisfont aux conditions:



a) sont des sous-ensembles de Ω;



b) pour deux sous-ensembles X, Y є β, il est vrai: (X, Y є γR) si le

sous - ensemble Y peut être obtenu à partir du sous-ensemble X en supprimant l'un de ses éléments maximaux (Fig. A et AA).





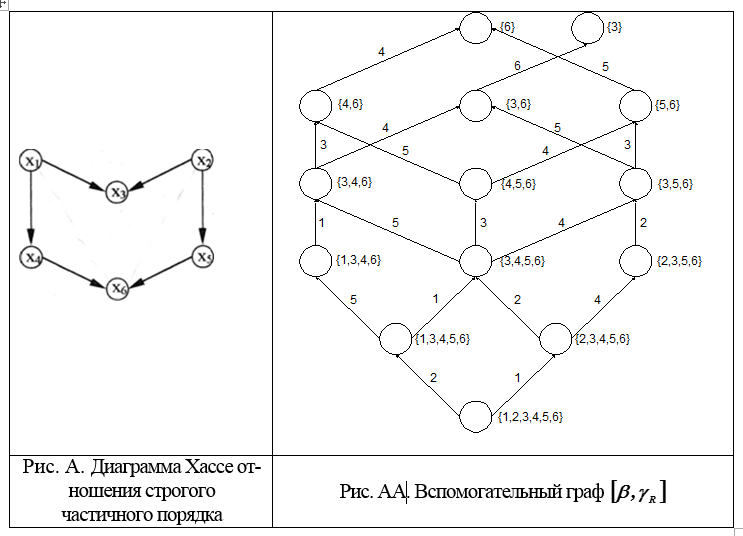
2. Pour chaque sous-ensemble à un élément de l'ensemble γR, écrivez sa numérotation unique. Pour obtenir toutes les numérotations d'un sous-ensemble X, il est nécessaire d'énumérer tous les sous-ensembles adjacents et pour chacun de ces sous-ensembles de continuer toutes ses numérotations. En conséquence, toutes les numérotations de l'ensemble Ω seront obtenues, c'est-à-dire toutes les extensions linéaires d'ordre R.



Le problème est de trouver toutes les ordonnances supplémentaires linéaires d'un ordre partiel, dont le diagramme est montré à la Fig. A. Il n'y a aucune information à cet égard, par exemple, si l'alternative domine$$$x_1$alternative $$$_2$ ou vice versa, et de même pour les paires $$$(_3, _6);(_4, _5)$... Cela signifie que A est un ordre partiel. Il existe de nombreuses (22) options pour construire un ordre linéaire, qu'il est souhaitable de ramener à un seul. Ceci est possible avec l'implication d'informations supplémentaires sur les alternatives obtenues à partir d'une étude détaillée de la situation.



1. Nous construisons un graphe auxiliaire [β, γR], en commençant par l'ensemble$$$(x_1, x_2, x_3,x_4, x_5, x_6)$et plus bas. Le nombre près de l'arc graphique indique en supprimant quel élément maximum le sous-ensemble vers lequel cette flèche est dirigée a été obtenu (Fig. AA).



2. Nous formons la table. AAA pour trouver toutes les numérotations des sous-ensembles qui sont des sommets du graphe [β, γR]. Le tableau est rempli ligne par ligne de haut en bas. Chaque ligne correspond à la numérotation du sous-ensemble enregistré dans la colonne de gauche du tableau (tableau AAA).



3. Lors de la composition de la numérotation d'un sous-ensemble X, constitué de k éléments, il est nécessaire de réécrire toute la numérotation précédemment écrite (pour le sous-ensemble précédent) des sous-ensembles Y є γR (x) et d'attribuer un numéro à l'élément qui complète Y à X.





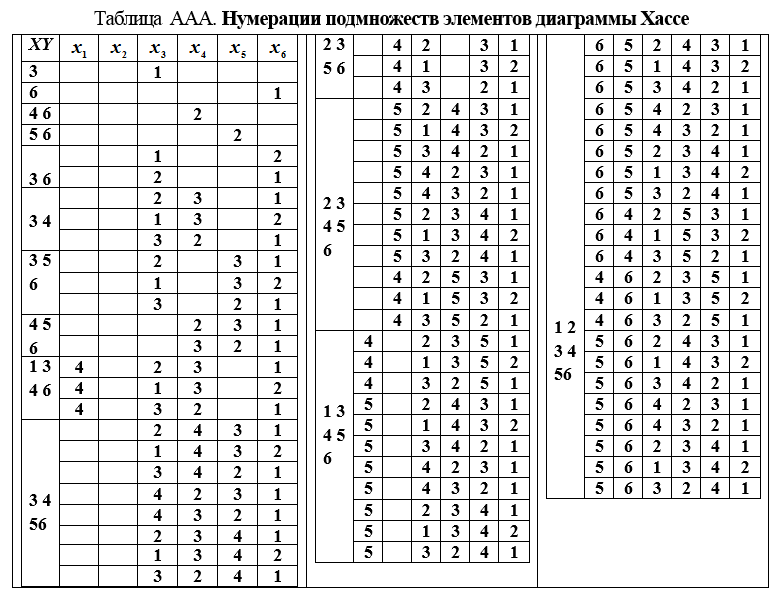
Le dernier bloc (inférieur) (tableau AAA) contient toutes les numérotations de la réorganisation linéaire de l'ensemble Ω. Une représentation graphique de ces réorganisations est illustrée à la Fig. AAA.





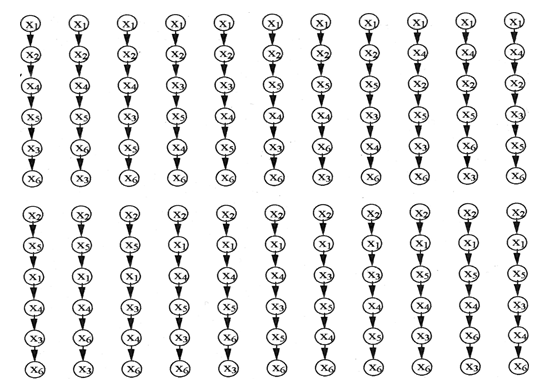
Figure: AAA. Représentation graphique des précommandes



Il est à noter qu'il y a 6 ordres linéaires sur un ensemble de 6 éléments! ou 720, et réordonnancement linéaire de l'ensemble Ω avec la relation donnée par le graphique illustré à la Fig. AA, 22. Cela suffit également pour prendre une décision.

Existe-t-il des possibilités de réduire le nombre de ces options? Oui il y en a.

Pour réduire le nombre de réorganisations linéaires, vous devez utiliser des informations supplémentaires.

Information additionnelle

Soit [Ω, R] la relation initiale, alors l'information supplémentaire peut être représentée par une relation δ sur l'ensemble Ω, où la condition (x, y) є δ, c'est-à-dire (x> y) est interprété comme un message indiquant que l'objet x domine l'objet y;

le rapport δ peut alors être considéré comme un ensemble de messages similaires d'information sur la dominance, donnés sous la forme d'un rapport binaire δ, il y a deux cas possibles lors de l'utilisation d'informations complémentaires:

1. le graphe de relations R∪δ contient des contours;
2. le graphe de la relation R∪δ ne contient aucun contour.

Dans le premier cas, le classement linéaire de l'ensemble Ω avec un rapport R∪δ donné sur celui-ci est effectué à l'aide de l'algorithme de classement

considéré précédemment.



Dans le second cas, le classement linéaire de l'ensemble Ω avec le rapport R∪δ donné sur celui-ci est effectué à l'aide de l'algorithme de réordonnancement linéaire

considéré ci-dessus. Il est à noter que la relation R∪δ, qui ne contient pas de contours, peut être non transitive et, par conséquent, ne pas être d'ordre partiel.



Pour sortir avec succès de cette situation, il est nécessaire que l'information supplémentaire δ et le rapport initial R soient donnés sous forme de diagrammes de Hasse, c'est-à-dire sans indication explicite de liens transitifs. La valeur des informations supplémentaires sera déterminée par le nombre de fois où le nombre d'ordres supplémentaires linéaires diminue lors de son utilisation.



Par exemple, si des informations sont reçues $$$x_2$ domine $$$x_4$, c'est à dire. $$$x_2>x_4$, alors le nombre de réordonnances linéaires diminuera de 22 à 19, et si des informations arrivent: $$$x_1>x_2$, puis le nombre de précommandes linéaires est divisé par deux. Ainsi, la question se pose: quelle information sera la plus précieuse, ou si vous ajoutez quel rapport δ, le nombre de commandes supplémentaires diminuera le plus?



Pour résoudre ce problème pour toutes les paires d'éléments$$$(x_i, x_j)$les ensembles Ω, qui ne sont pas inclus dans la relation R, dans le bloc inférieur du tableau. AAA, vous devez calculer$$$n_{ij}$ - combien de fois le numéro d'article $$$x_i$ plus de numéro d'article $$$x_j$, c'est à dire. élément$$$x_i$ se dresse au-dessus de l'élément $$$x_j$ et $$$n_{ji}$ - combien de fois un article $$$x_j$ se dresse au-dessus de l'élément $$$x_i$...

La valeur des informations supplémentaires sur la relation dans cette paire sera d'autant plus élevée que la différence sera petite.$$$|n_{ij} - n_{ji}|$... Plus grand des nombres$$$n_{ij}, n_{ji}$sera égal au nombre de réordres de l'ensemble [Ω, R∩δ]. Pour l'exemple considéré, nous obtenons un résumé des caractéristiques de la représentation graphique des réordonnances





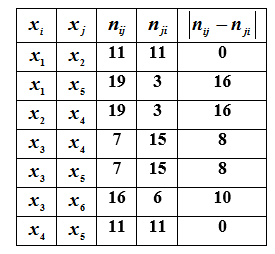
De l'analyse du tableau, il s'ensuit que les

informations les plus utiles seront les informations sur la relation par paires$$$(x_1, x_2)$ et $$$(x_4, x_5)$... L'obtention d'informations supplémentaires sur la relation dans l'une de ces paires conduit à diviser par deux le nombre d'ordonnances supplémentaires linéaires.

Conclusion

La formulation et la solution du ZPR n'est possible que dans une situation de nombreuses alternatives et le choix de la meilleure. S'il n'y a pas le choix, suivez le chemin sur lequel vous vous trouvez.

Les décisions prises par un décideur sont basées sur sa préférence, qui est décrite par une relation de préférence. La présence de la relation vous permet de construire un modèle mathématique pour la recherche. L'incertitude dans les préférences est éliminée en utilisant des informations supplémentaires qui ne sont pas expertes.



Une attention particulière est accordée à la prise en compte des mesures et des estimations des valeurs des indicateurs des propriétés des objets. Des exemples de diverses échelles souvent ignorées sont donnés.

Les formulations possibles de ZPR et les informations nécessaires à leur solution sont répertoriées.



À l'aide d'un exemple numérique spécifique, l'application de méthodes algébriques pour résoudre ZPR est montrée, sans l'utilisation d'échantillons statistiques et de méthodes de traitement empiriques.

La méthode est basée sur le résultat du théorème sur la possibilité d'étendre un ordre partiel à un ordre linéaire (parfait).

Liste de la littérature utilisée

1. Berge K. Théorie des graphes et son application. - M .: IL, 1962 .-- 320 p.

2. Vaulin AE Mathématiques discrètes dans les problèmes de sécurité informatique. Partie I.SPb.: VKA nommé d'après A.F. Mozhaisky, 2015 .-- 219 p.

3. Vaulin AE Mathématiques discrètes dans les problèmes de sécurité informatique Ch. II. SPb.: VKA nommé d'après A.F. Mozhaisky, 2017 .-- 151 p.

4. Vaulin AE Méthodes de recherche des complexes informatiques. Problème 2. - L.: VIKI eux. A.F. Mozhaisky, 1984 .-- 129 p.

5. Vaulin AE Méthodologie et méthodes d'analyse des systèmes informatiques. Numéro 1.– L.: VIKI im. A.F. Mozhaisky, 1981 .-- 117 p.

6. Vaulin AE Méthodes de traitement numérique des données: transformations orthogonales discrètes. - SPb.: VIKKI eux. A.F. Mozhaisky, 1993 .-- 106 p.

7. Kuzmin VB Construction de solutions de groupe dans des espaces de relations binaires claires et floues. - M .: Nauka, 1982. - 168 p.

8. Makarov IM et al. La théorie du choix et de la prise de décision - Moscou: Fizmatlit, 1982. –328 p. 52.

9. Rosen V.V. Objet - optimalité - solution - M .: Radio et communication, 1982. - 169 p.

10. Szpilraijn E Sur Textension de l'ordre partiel. - Fundam. math., 1930, vol. 16, pp. 386-389.