🧝🏼 🧖🏾 🐺 Où résoudre les tâches analytiques des équipes Yandex? Concours et analyse 👩‍👧‍👧 🌨️ 😹

La phase d'essai du championnat de programmation de la Coupe Yandex commence aujourd'hui . Cela signifie que vous pouvez utiliser le système Yandex.Contest pour résoudre des problèmes similaires à ceux qui seront dans le tour de qualification. Jusqu'à présent, le résultat n'affecte rien.

Dans le post, vous trouverez les conditions des tâches de la piste analytique et des analyses, qui sont délibérément cachées dans des spoilers. Vous pouvez voir la solution ou essayer de faire les tâches vous-même en premier. Le contrôle est automatique - le Concours rapportera immédiatement le résultat, et vous aurez la possibilité de proposer une autre solution.

A. Comptez les menteurs dans le pays

^{Résoudre dans le concours}

10 000 personnes vivent dans l'État. Ils sont divisés en amoureux de la vérité et en menteurs. Les amateurs de vérité disent la vérité avec une probabilité de 80%, et les menteurs - avec une probabilité de 40%. L'État a décidé de compter les amateurs de vérité et les menteurs sur la base d'une enquête menée auprès de 100 habitants. Chaque fois qu'une personne choisie au hasard est posée, "Êtes-vous un menteur?" - et notez la réponse. Cependant, une personne peut participer à l'enquête plusieurs fois. Si un résident a déjà participé à l'enquête, il répond de la même manière que la première fois. Nous savons qu'il y a 70% d'amateurs de vérité et 30% de menteurs. Quelle est la probabilité que l'État sous-estime le nombre de menteurs, c'est-à-dire qu'une enquête montrera qu'il y a moins de 30% de menteurs? Donnez votre réponse en pourcentage avec un point comme séparateur, arrondissez le résultat au centième près (exemple de saisie: 00,00).

Décision

1. «» « ?».

«, » «» «» .

«, » :

: «» * = 0,2 * 0,7.

: «» * ( – ) + «» * ( ) = «» * = 0,2 * 0,7.

«, » 0,14 , . .

, «, » : 0,2 * 0,7 + 0,4 * 0,3 = 0,26.

2. .

, , — n = 100, p = 0,26.

, 30 (30% 100 ): P (x < 30). n = 100, p = 0,26 0,789458. : stattrek.com/online-calculator/binomial.aspx.

, : 78,95.

B. Saison théâtrale et téléphones

^{Décidez dans le concours La}

billetterie internationale a décidé de faire le point sur la saison théâtrale. Comme l'une des mesures, le chef de projet veut compter le nombre d'utilisateurs qui ont acheté des billets pour différentes performances.

Lors de l'achat d'un billet, l'utilisateur indique son numéro de téléphone. Vous devez trouver l'émission avec le plus grand nombre de numéros de téléphone uniques. Et comptez le nombre de numéros de téléphone uniques correspondants.

Format d'entrée

Les journaux d'achat sont disponibles dans le fichierticket_logs.csv. La première colonne contient le nom de la performance de la base de données du service. Dans le second - le numéro de téléphone que l'utilisateur a laissé lors de l'achat. Notez que par souci de complot, les indicatifs téléphoniques des pays ont été remplacés par des zones actuellement non desservies.

Format de sortie

Le nombre de nombres uniques.

Décision

main.py.

. . 801–807.

:

1. 8-(801)-111-11-11

2. 8-801-111-11-11

3. 8801-111-11-11

4. 8-8011111111

5. +88011111111

6. 8-801-flowers, — ( )

:

1. 1–4 replace.

2. 5 , 1. 11 , .

3. 6 , . , .

, . .

C. Calculer pFound

^{Résoudre dans le concours}

L'archivecontient trois fichiers texte:

qid_query.tsv - ID de requête et texte de requête, séparés par des tabulations;
qid_url_rating.tsv - ID de la demande, URL du document, pertinence du document par rapport à la demande;
hostid_url.tsv - ID d'hôte et URL du document.

Il est nécessaire d'afficher le texte de la demande avec la valeur maximale de la métrique pFound, calculée à partir des 10 premiers documents. L'émission sur demande se fait selon les règles suivantes:

Il ne peut y avoir qu'un seul document émis par un hôte. S'il existe plusieurs documents pour la demande avec le même identifiant d'hôte, le document le plus pertinent est pris (et si plusieurs documents sont les plus pertinents, l'un d'entre eux est pris).
Les documents à la demande sont triés par ordre décroissant de pertinence.
Si plusieurs documents provenant d'hôtes différents ont la même pertinence, leur ordre peut être arbitraire.

Formule de calcul de pFound:

pFound =

\sum_{i = 1}^{10}

$\sum_{i=1}^{10}$ pLook [i] ⋅ pRel [i]

pLook [1] = 1

pLook [i] = pLook [i - 1] ⋅ (1 - pRel [i - 1]) ⋅ (1 - pBreak)

pBreak = 0,15

Format de sortie

Le texte de la demande avec la valeur métrique maximale. Par exemple, pour open_task.zip, la bonne réponse est:

Décision

. - — pFound . pandas — .

import pandas as pd

#  
qid_query = pd.read_csv("hidden_task/qid_query.tsv", sep="\t", names=["qid", "query"])
qid_url_rating = pd.read_csv("hidden_task/qid_url_rating.tsv", sep="\t", names=["qid", "url", "rating"])
hostid_url = pd.read_csv("hidden_task/hostid_url.tsv", sep="\t", names=["hostid", "url"])

#  join  ,     url   
qid_url_rating_hostid = pd.merge(qid_url_rating, hostid_url, on="url")

def plook(ind, rels):
 if ind == 0:
 return 1
    return plook(ind-1, rels)*(1-rels[ind-1])*(1-0.15)

def pfound(group):
 max_by_host = group.groupby("hostid")["rating"].max() #   
 top10 = max_by_host.sort_values(ascending=False)[:10] #  -10    
 pfound = 0
    for ind, val in enumerate(top10):
 pfound += val*plook(ind, top10.values)
 return pfound

qid_pfound = qid_url_rating_hostid.groupby('qid').apply(pfound) #   qid   pfound
qid_max = qid_pfound.idxmax() #  qid   pfound

qid_query[qid_query["qid"] == qid_max]

D. Tournoi sportif

^{Résoudre en concours}

Délai pour le test	2 sec
Limite de mémoire par test	256 Mo
Contribution	entrée standard ou input.txt
Production	sortie standard ou output.txt

Pendant que Masha était en vacances, ses collègues ont organisé un tournoi d'échecs selon le système olympique. En se reposant, Masha n'a pas prêté beaucoup d'attention à cette entreprise, elle peut donc à peine se souvenir qui a joué avec qui (il n'est pas question de l'ordre des jeux). Soudain, Masha eut l'idée qu'il serait bien d'apporter un souvenir au vainqueur du tournoi de vacances. Masha ne sait pas qui a remporté le dernier match, mais elle peut facilement savoir qui y a joué, si seulement elle se souvenait correctement des paires jouées. Aidez-la à vérifier si tel est le cas et à identifier les gagnants potentiels.

Format d'entrée

La première ligne contient un entier 3 ≤ n ≤ 2 ¹⁶ - 1, n = 2 ^k - 1 - le nombre de parties passées. Les n lignes suivantes contiennent deux noms de famille des joueurs (en lettres majuscules latines) séparés par un espace. Les noms des joueurs sont différents. Tous les noms de famille sont uniques, il n'y a pas d'homonyme parmi les collègues.

Format d'entrée

Imprimer "PAS DE SOLUTION" (sans guillemets) si Masha a mal mémorisé les jeux et qu'il est impossible d'obtenir un tournoi selon le système olympique en utilisant cette grille. Si la grille du tournoi est possible, imprimez deux noms de famille sur une ligne - les noms des candidats pour la première place (l'ordre n'est pas important).

Exemple 1

Contribution	Production
`7 GORBOVSKII ABALKIN SIKORSKI KAMMERER SIKORSKI GORBOVSKII BYKOV IURKOVSKII PRIVALOV BYKOV GORBOVSKII IURKOVSKII IURKOVSKII KIVRIN`	`IURKOVSKII GORBOVSKII`

Exemple 2

Contribution	Production
`3 IVANOV PETROV PETROV BOSHIROV BOSHIROV IVANOV`	`NO SOLUTION`

Notes Le

système olympique, également connu sous le nom de playoffs, est un système d'organisation de compétition dans lequel un compétiteur est éliminé d'un tournoi après la première défaite. Vous pouvez en savoir plus sur le système olympique sur Wikipedia .

Schéma du premier test à partir de la condition:

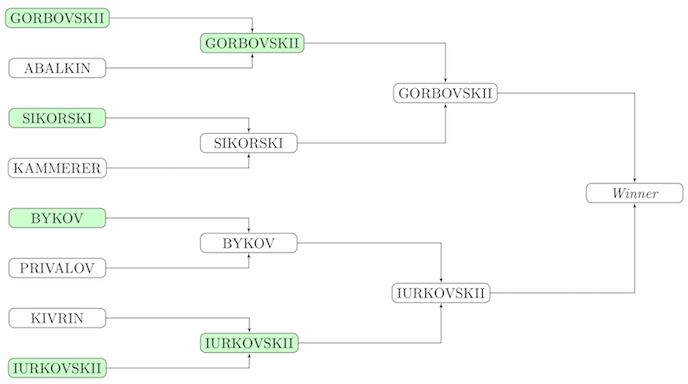
Décision

n = 2^k – 1 k. , i- , n_i. , ( k ). , . , i  j min(n_i, n_j), - ( ). r (i, j), min(n_i, n_j) = r. :

. 2^k – 1 , :

1. .

2. r 2^{k – r}.

. : , . k.  k = 1 — . k – 1 -> k.

-, , . , q . , q- . , 1, 2, ..., q. , , , , 2^k. , 2^{k – 1}   n_i = 1. .

, 2^{k – 1} n_i > 1 — . , n_i = 1 2^{k – 1}, . , : n_i = 1, — n_i > 1.   k – 1 ( n_i 1). , .

import sys
import collections

def solve(fname):
    games = []
    for it, line in enumerate(open(fname)):
        line = line.strip()
        if not line:
            continue
        if it == 0:
            n_games = int(line)
            n_rounds = n_games.bit_length()
        else:
            games.append(line.split())

    gamer2games_cnt = collections.Counter()
    rounds = [[] for _ in range(n_rounds + 1)]

    for game in games:
        gamer_1, gamer_2 = game
        gamer2games_cnt[gamer_1] += 1
        gamer2games_cnt[gamer_2] += 1

    ok = True
    for game in games:
        gamer_1, gamer_2 = game
        game_round = min(gamer2games_cnt[gamer_1], gamer2games_cnt[gamer_2])
        if game_round > n_rounds:
            ok = False
            break
        rounds[game_round].append(game)

    finalists = list((gamer for gamer, games_cnt in gamer2games_cnt.items() if games_cnt == n_rounds))

    for cur_round in range(1, n_rounds):
        if len(rounds[cur_round]) != pow(2, n_rounds - cur_round):
            ok = False
            break
        cur_round_gamers = set()
        for gamer_1, gamer_2 in rounds[cur_round]:

            if gamer_1 in cur_round_gamers or gamer_2 in cur_round_gamers:
                ok = False
                break
            cur_round_gamers.add(gamer_1)
            cur_round_gamers.add(gamer_2)

    print ' '.join(finalists) if ok else 'NO SOLUTION'

def main():
    solve('input.txt')

if name == '__main__':
    main()

Pour résoudre les problèmes des autres pistes du championnat, vous devez vous inscrire ici .

Où résoudre les tâches analytiques des équipes Yandex? Concours et analyse

A. Comptez les menteurs dans le pays

B. Saison théâtrale et téléphones

C. Calculer pFound

D. Tournoi sportif

More articles: