Craignant un ordinateur quantique capable de casser les méthodes de cryptage modernes, les cryptographes du monde entier continuent à rechercher des systèmes cryptographiques résistants à l'attaque d'un ordinateur quantique. L'un de ces cryptosystèmes a été inventé en 1978 et est basé sur la théorie du codage algébrique. Cet article fournit une vue d'ensemble de la cryptographie de code basée sur des codes de contrôle de parité à faible densité (ou simplement des codes LDPC). Je demande à tout le monde intéressé sous le chat.
Contenu
- introduction
- Codes linéaires
- Cryptographie de code
- Codes basse densité (LDPC)
- Cryptographie LDPC
- Conclusion
- Littérature
introduction
, , . , , , . , , .
:

, , 0 1.
— . , :
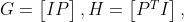
, . , : . : , — , — .
, . , . -, . , — ( , , 1).
, . (maximum likelihood decoding) , . :

: ( ). ( ).
(, LDPC , , belief propagation bit-flipping, ). — NP- .
: NP- , .
:
- (, )
- ,
- , , ,
-
- . .
:
- :
- : ( )
-.
:
- — (k, n)- (n, k)- ,
- (k, k)-
- (n, n)-
- : ,
- :
: , , , t , , , .
( 3 !), . , , .
:
- :
c:
- c ,
:
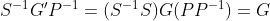
, . : , -, , -, LDPC, LRPC, , - .
, : . .
, :
- MDPC ( LDPC )
LDPC — MDPC .
(LDPC)
, — .
, LDPC , .
LDPC
:
- : 0 n. .
- . "" "" ( . "soft-decision" "hard-decision" decoding).
- : LDPC .
- (QC-LDPC) .
LDPC
LDPC -, :
- LDPC "" .
- .
- QC-LDPC .
:
- LDPC ( t , density evolution).
- (, ).
- , .
LDPC
LDPC: MDPC (QC-MDPC).
MDPC
MDPC (Moderate Density Parity-Check) — "" LDPC . LDPC w 10, MDPC , n — - (, ).
MDPC , : .
(QC-LDPC) . (n, n)-, , — :
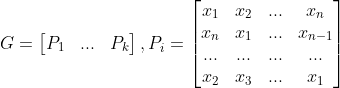
, , : , .
, , (p, n)-QC-LDPC n = 9602 p = 4801 ( ):
- P(n, n): ~11 Mb --> P’(n): ~9.5 Kb. , .
- G(n, p): ~5.5 Mb --> G’(n): ~1.2 Kb.
- S(p, p): ~2.75 Mb --> S’(p): ~0.6 Kb. S , , .
: 1760 ! , .
, .
, - (1024, 524, 101)- 50 ( ).
: MDPC n = 9602 w = 90 80 . , (, ), .
— . , .
, : .
, , , — . , . , .
- A Public-Key Cryptosystem Based On Algebraic Coding Theory (R. J. McEliece)
- An Introduction to Low-Density Parity Check Codes (Daniel J. Costello, Jr.)
- On the Usage of LDPC Codes in the McEliece Cryptosystem (Marco Baldi)
- LDPC codes in the McEliece cryptosystem: attacks and countermeasures (Marco Baldi)
- QC-LDPC Code-Based Cryptography (Marco Baldi)
- MDPC-McEliece: New McEliece Variants from Moderate Density Parity-Check Codes (Rafael Misoczki and Jean-Pierre Tillich and Nicolas Sendrier and Paulo S. L. M. Barreto)
- Modern Coding Theory (Tom Richardson, Rudiger Urbanke)