🐜 👨🏻‍🎨 🚣 Comment dessiner une étoile (et plus) en coordonnées polaires 🚴🏻 🤞 👺

La question de la formule d'un polygone en coordonnées polaires se pose régulièrement sur les ressources thématiques - et reste tout aussi régulièrement sans réponse claire. Dans le meilleur des cas, on trouve une solution à travers la fonction du reste de la division - qui n'est pas "propre" d'un point de vue mathématique, puisqu'elle ne permet pas d'effectuer des transformations analytiques sur la fonction. Apparemment, les vrais mathématiciens sont trop occupés à résoudre des problèmes du millénaire et à chercher une simple preuve du théorème de Fermat pour prêter attention à ces problèmes banals. Heureusement, dans ce domaine, l'imagination est plus importante que la connaissance, et pour résoudre ce problème, vous n'avez pas besoin d'être professeur de sciences topologiques - les connaissances au niveau de l'école suffisent.

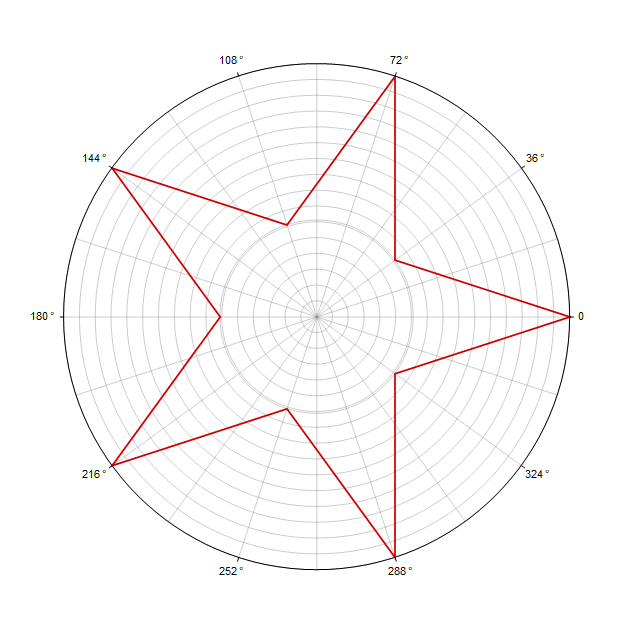
La formule d'un polygone équilatéral en coordonnées polaires semble très simple

ρ = \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n ϕ)) + π m}{2 n})}

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

et a les paramètres suivants:

ϕ

$\phi$ - angle;

n

$n$ - le nombre de sommets convexes;

m

$m$ - détermine le nombre de sommets des côtés sur une ligne droite. Des valeurs négatives sont également autorisées pour cela - le signe déterminera dans quelle direction l'étoile se pliera;

k

$k$ - rigidité - à

k = 0

$k=0$ nous obtenons un cercle indépendamment des autres paramètres, car

k = 1

$k=1$ - un polygone avec des lignes droites, à des valeurs intermédiaires de

0

$0$ avant

1

$1$ - figures intermédiaires entre un cercle et un polygone.

Avec cette formule, vous pouvez dessiner une étoile de deux manières:

1)

n = 5, m = 3

$n=5, m=3$

n = 5 / 4, m = 0

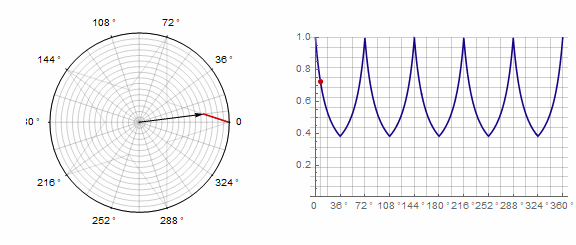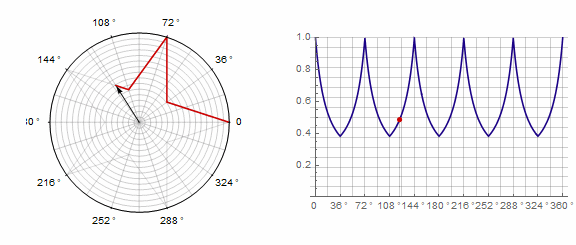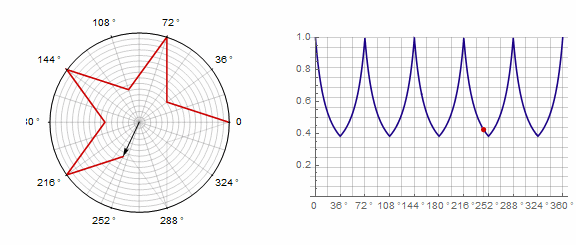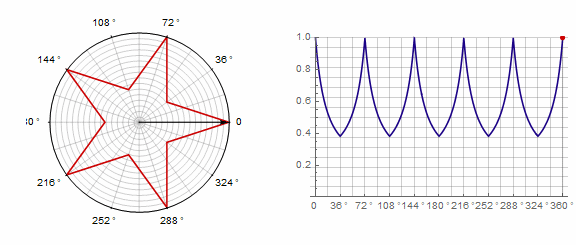
$n=5/4,m=0$ ... Dans ce cas, vous devez effectuer deux tours au lieu d'un:

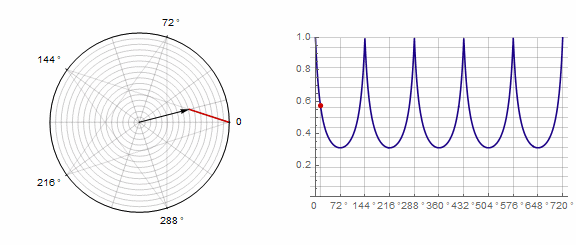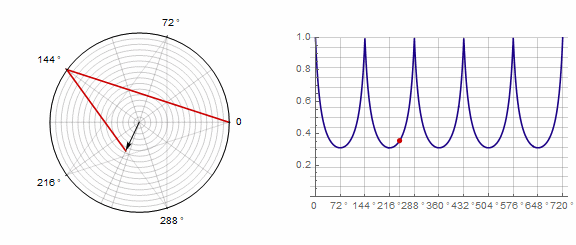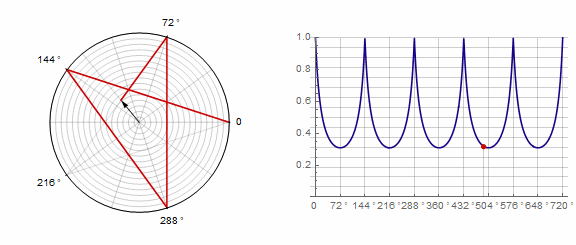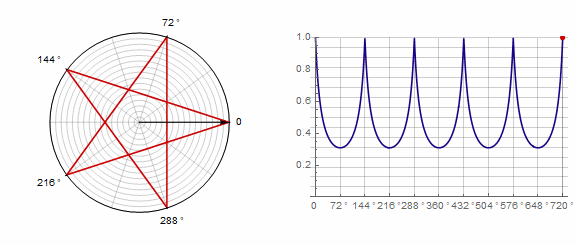
Paramètre

m

$m$ affecte le polygone comme suit (ici il passe de -1 à 5):

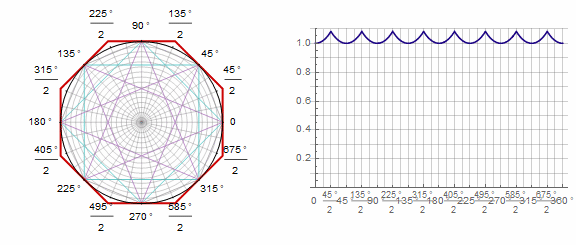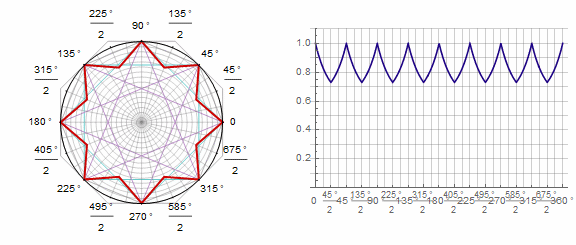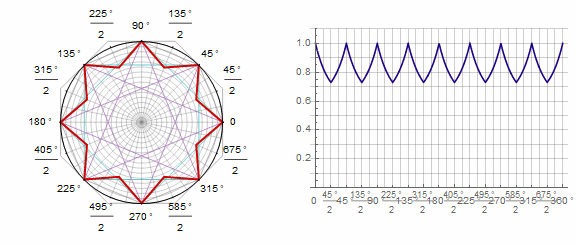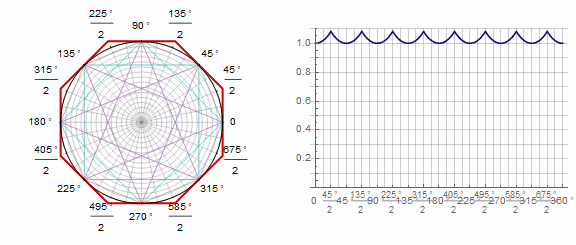
Paramètre

k

$k$ en animation:

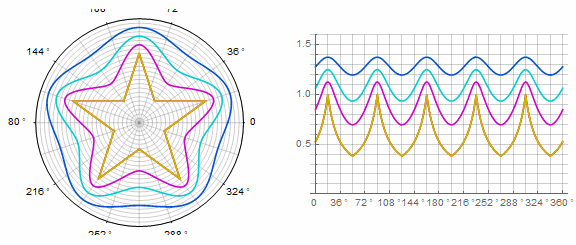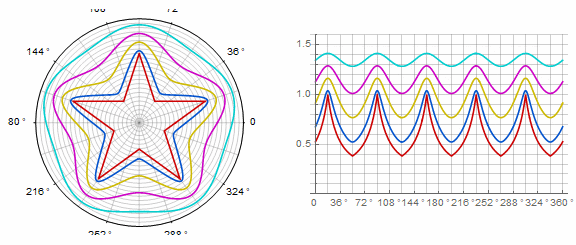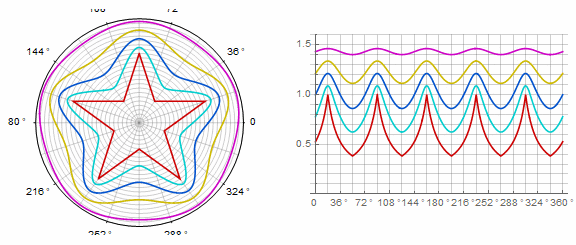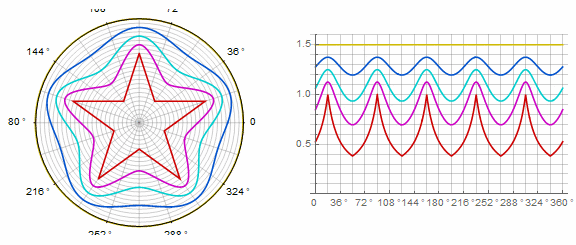
Forme complexe et modifications

Vous pouvez réécrire la formule originale sous une forme complexe et, malgré la présence d'unités imaginaires, la valeur du rayon restera toujours valide:

ρ = \frac{4^{1 / n} {(\sqrt{1 - k^{2}} + i k)}^{- 1 / n} (1 + {(\sqrt{1 - k^{2}} + i k)}^{2 / n} e^{\frac{i π m}{n}}) {(\sqrt{1 - k^{2} \cos^{2} (n ϕ)} + i k \cos (n ϕ))}^{1 / n}}{4^{1 / n} + e^{\frac{i π m}{n}} {(2 \sqrt{1 - k^{2} \cos^{2} (n ϕ)} + 2 i k \cos (n ϕ))}^{2 / n}}

$\small\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

À première vue, cela peut sembler inutile, car la formule est devenue un peu plus lourde - mais ne sautez pas aux conclusions. Premièrement, il n'y a pas d'arc sinus, ce qui change complètement la signification mathématique de la formule et vous permet de regarder différemment la construction d'un polygone étoilé. Deuxièmement, il peut également être utilisé pour obtenir des formules compactes pour des cas particuliers, par exemple

\frac{i^{t} {(i^{n t})}^{1 / n}}{1 + {(i^{n t})}^{2 / n}}

$\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ ... Troisièmement (et le plus intéressant), il peut être modifié de manière créative et obtenir d'autres formes inattendues. Pour que l'apparition d'une éventuelle composante imaginaire dans le rayon ne provoque pas d'ambiguïté dans le calcul, elle peut être immédiatement réduite en coordonnées cartésiennes en multipliant par

e^{i ϕ}

$e^{i \phi }$ ... Voici des exemples de certaines des modifications:

\frac{(- 1)^{2 / 3} e^{i ϕ} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{1 / 3}}{(- 1)^{2 / 3} + 2^{2 / 3} {(i \cos (3 ϕ) + \sqrt{\sin^{2} (3 ϕ)})}^{2 / 3}}

$\frac{(-1)^{2/3} e^{i \phi } \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{1/3}} {(-1)^{2/3}+2^{2/3} \left(i \cos (3 \phi )+\sqrt{\sin ^2(3 \phi )}\right)^{2/3}}$

\frac{e^{i ϕ} \sqrt{i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}}}{e^{i / 2} + \sqrt{2} {(i \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)})}^{3 / 2}}

$\frac{e^{i \phi } \sqrt{i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}}{e^{i/2}+\sqrt{2} \left(i \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}\right)^{3/2}}$

\frac{e^{\frac{1}{4} i (4 ϕ + π)}}{2 \sqrt{(- 1)^{1 / 4} \cos (2 ϕ) + \sqrt{\sin^{2} (2 ϕ)}} - 1 - i}

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{(-1)^{1/4} \cos (2 \phi )+\sqrt{\sin ^2(2 \phi )}}-1-i}$

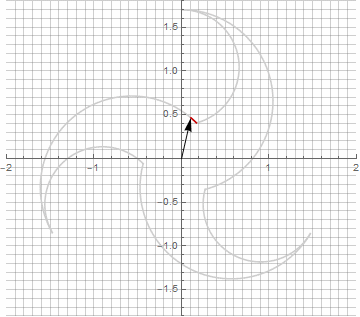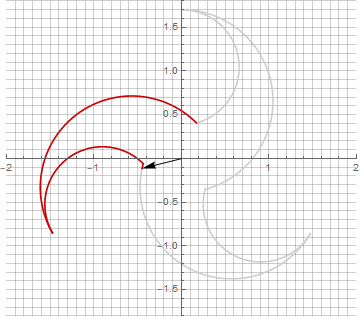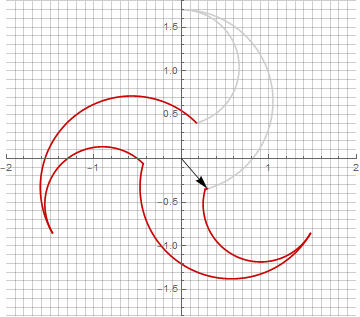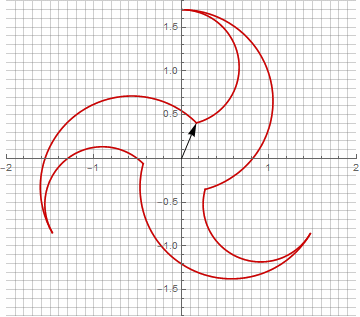
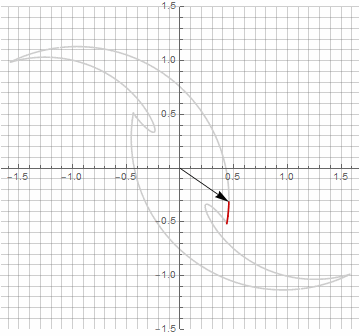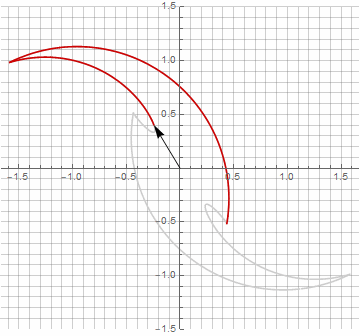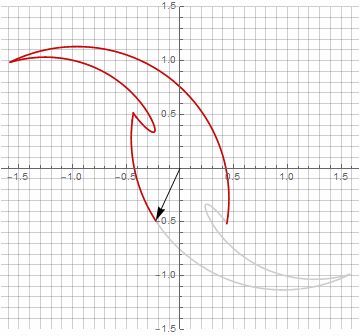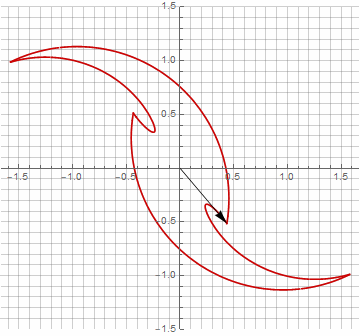
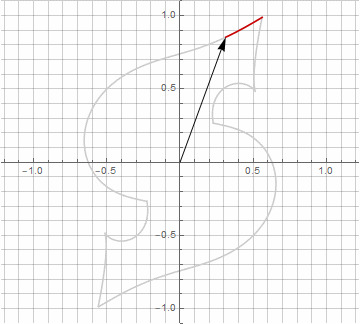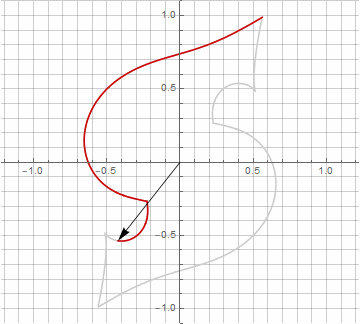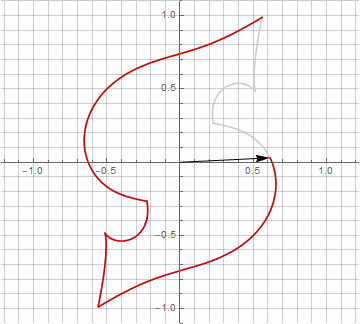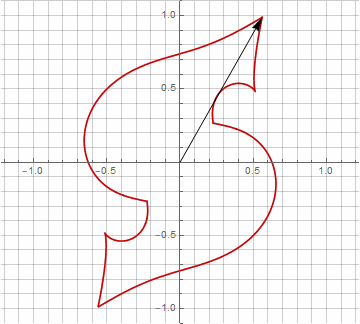
Comme vous l'avez probablement remarqué, la rotation du vecteur a cessé d'être uniforme - et précisément à cause de l'apparition de la composante imaginaire dans le rayon.

Quads et trucs

Notre formule a un cas spécial merveilleux - un carré, dont la formule peut s'écrire

ρ = \frac{2}{\sqrt{2 + \sqrt{2 + 2 \cos (4 ϕ)}}}

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 ϕ)}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

(choisissez celui que vous préférez).

Dans un cas un peu plus développé, vous pouvez définir des figures intermédiaires entre un cercle et un carré en passant par un point

(k, k)

$(k,k)$ en surface

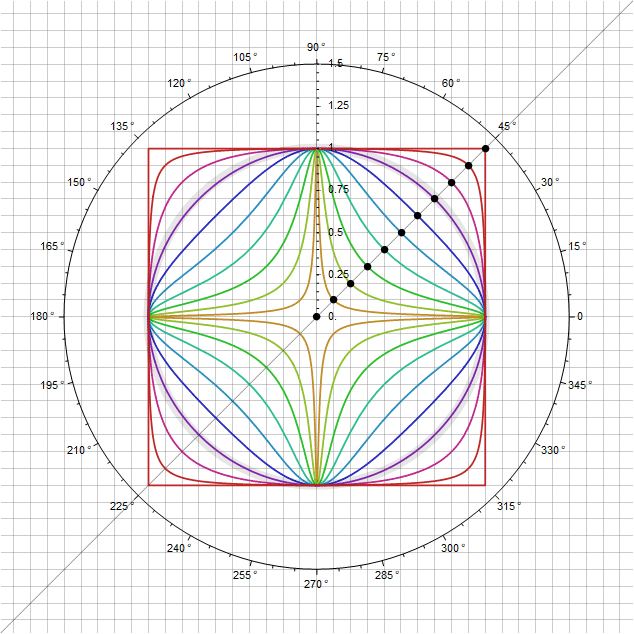
ρ = \sqrt{\frac{2}{1 + \sqrt{1 - \frac{(2 k^{2} - 1) \sin^{2} (2 ϕ)}{k^{4}}}}}

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

Vous pouvez également ajouter des variations à ces formes tout en conservant la condition qu'elles passent par le point

(k, k)

$(k,k)$ - moduler directement le paramètre lui-même

k

$k$ en fonction de l'angle de sorte qu'en passant par la diagonale, son multiplicateur est égal à un. Par exemple, en remplaçant à la place

k

$k$ une fonction

\frac{k}{1 - z \cos^{2} (2 ϕ)}

$\frac{k}{1-z \cos ^2(2 \phi )}$ , nous obtiendrons un paramètre supplémentaire

z

$z$ avec lesquels des courbes supplémentaires peuvent être ajustées. En particulier, pour

z = 1 / 4

$z=1/4$ vous obtenez ce qui suit:

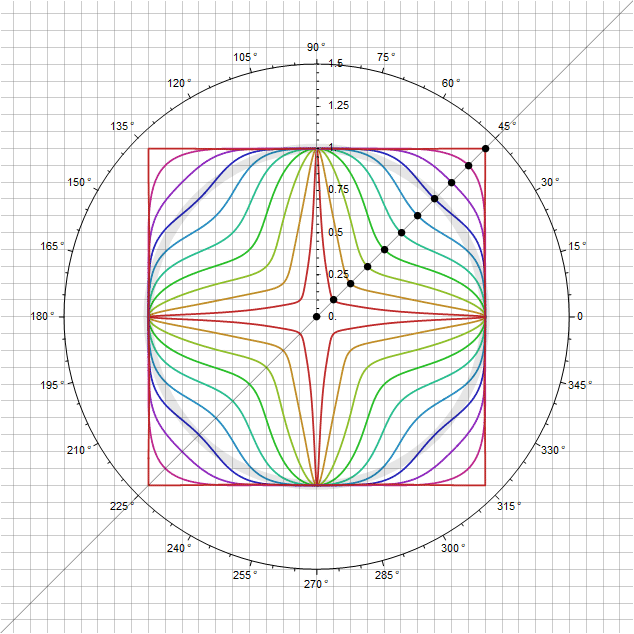
Dans un cas encore plus développé, vous pouvez définir non seulement un carré, mais un rectangle, et toujours en coordonnées polaires:

ρ = \sqrt{\frac{4 a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (\sqrt{1 - \frac{4 a^{2} b^{2} k \sin^{2} (2 ϕ)}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}} + 1)}}

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

Et même calculer sa surface (via des intégrales elliptiques):

S = 4 a b \frac{(k - 1) K (k) + E (k)}{k}

$S=4 a b\frac{(k-1) K(k)+E(k)}{k}$

Remarque

k

$k$ (

0

$0$

1

$1$ ) ,

π a b

$\pi a b$

4 a b

$4 a b$ .

Cela permettra de créer des profils avec une transition d'un cercle à un rectangle avec une zone de section contrôlée. Ici, l'aire est constante:

Et ici, la zone se développe de manière exponentielle:

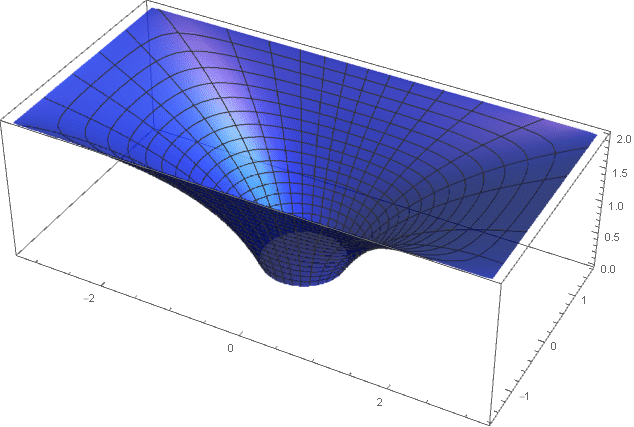
Aller aux coordonnées cartésiennes

Toute formule en coordonnées polaires peut être exprimée par une équation en coordonnées cartésiennes, et au moins de deux manières - en fonction de la forme du gradient sur le bord de la figure qui changera. Pour ce faire, il suffit de calculer l'angle passant par l'arc tangente des coordonnées et d'amener la formule à une constante passant par le vecteur rayon en soustrayant

0 = \sqrt{x^{2} + y^{2}} - \frac{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

ou division

1 = \frac{\sqrt{x^{2} + y^{2}} \cos (\frac{2 \sin^{- 1} (k \cos (n \tan^{- 1} (x, y))) + π m}{2 n})}{\cos (\frac{2 \sin^{- 1} (k) + π m}{2 n})}

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

La deuxième option est préférable car elle donne des dégradés droits le long des côtés du polygone.

Remarque

, (0,0) - — , , (

- \cos (\frac{2 \sin^{- 1} (k) + π m}{2 n}) \sec (\frac{2 \sin^{- 1} (k \cos (\frac{π n}{2})) + π m}{2 n})

$-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ ).

\cos (n \tan^{- 1} (x, y))

$\cos \left(n \tan ^{-1}(x,y)\right)$

\frac{(x + i y)^{n} + (x - i y)^{n}}{2 {(x^{2} + y^{2})}^{n / 2}}

$\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , A034839.

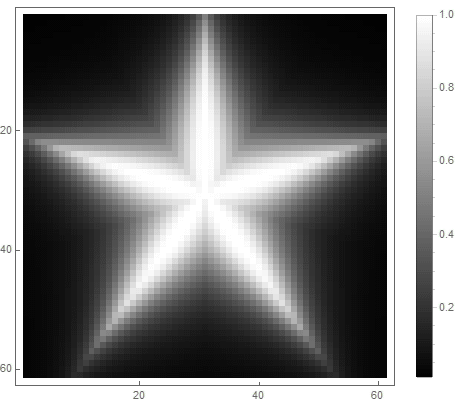
La valeur de la formule du côté droit de l'équation (dans le 2ème cas) passera de

0

$0$ avant

1

$1$ si point

(x, y)

$(x,y)$ pénètre dans la figure, et de

1

$1$ à l'infini - sinon. En choisissant différentes fonctions pour le convertir en luminosité, vous pouvez obtenir différentes options de pixellisation. Pour l'exposant (

e^{- x - 1}

$e^{-x-1}$ pour le premier et

e^{- x}

$e^{-x}$ pour la deuxième option) nous obtenons

ou, si avec saturation

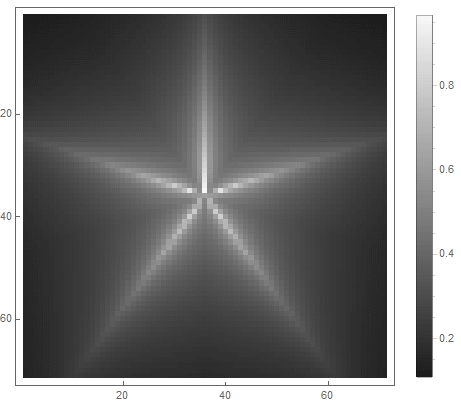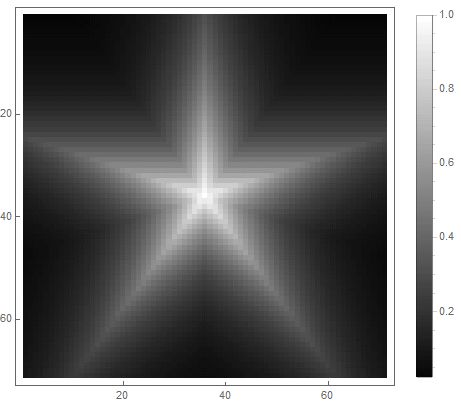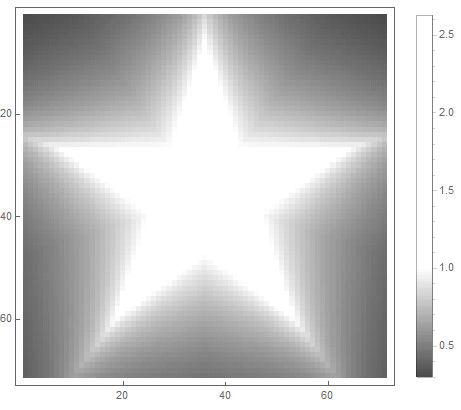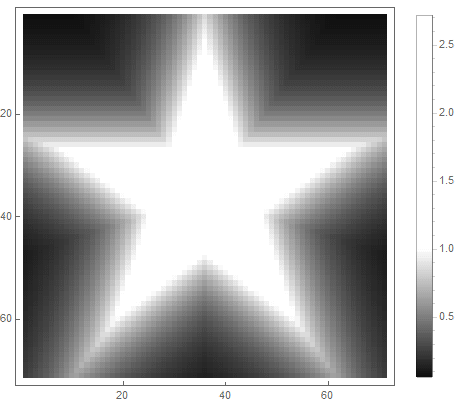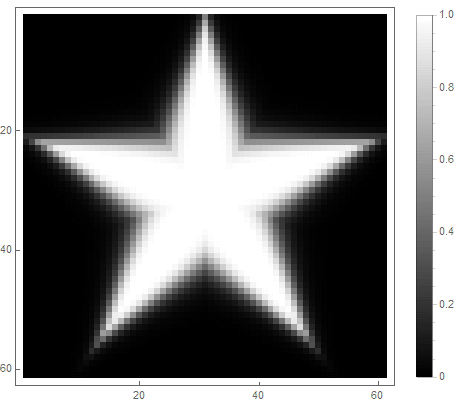
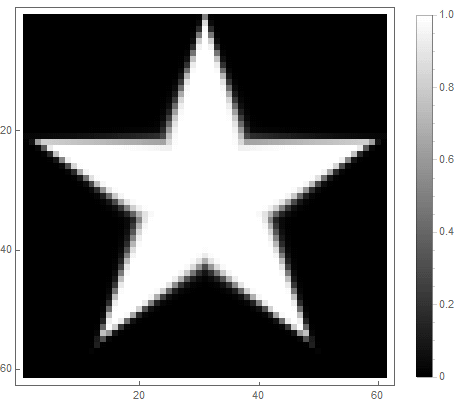
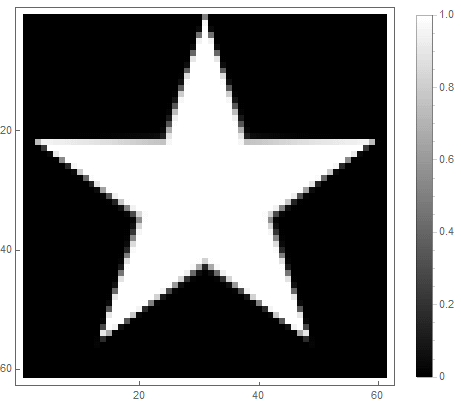
Un filtre passe-bas classique peut être utilisé

\frac{1}{1 + x^{p}}

$\frac{1}{1+x^p}$ , dans lequel

p

$p$ - l'ordre du filtre, qui détermine le degré d'atténuation.

Pour la première option:

Et pour le second:

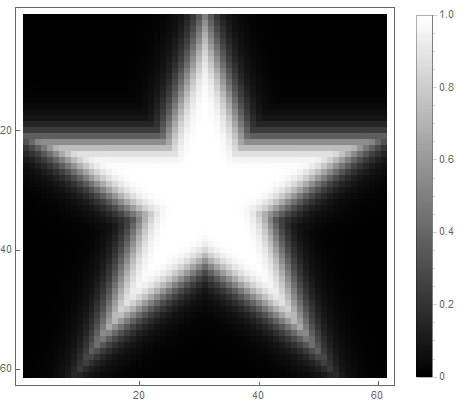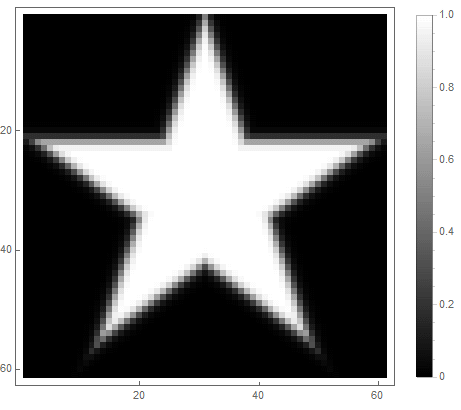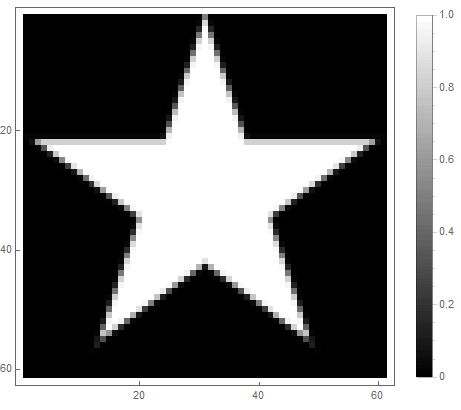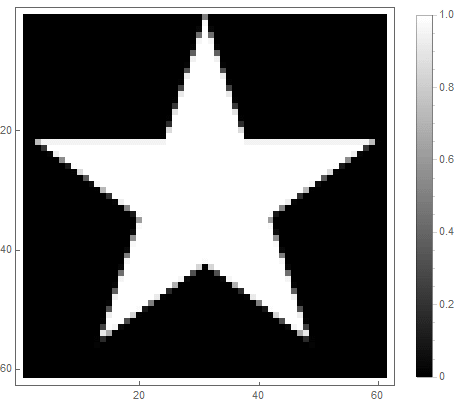Vous pouvez également utiliser une fonction continue par morceaux en définissant explicitement les limites d'interpolation.

En plus de la pixellisation en tant que telle, vous pouvez également définir des déformations - par exemple, presser un damier dans un cercle:

Ou même le tirer sur une sphère:

Formule

x = \frac{u}{\sqrt{\frac{2}{1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$x=\frac{u}{\sqrt{\frac{2}{1+ \left| \frac{u^2-v^2}{u^2+v^2} \right|}}}$

y = \frac{v}{\sqrt{1 + \frac{2}{| \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |}}}

$y=\frac{v}{\sqrt{1+\frac{2}{\left| \frac{u^2-v^2}{u^2+v^2}\right| }}}$

z = \sqrt{1 - \frac{1}{2} u^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |) - \frac{1}{2} v^{2} (1 + | \frac{u^{2} - v^{2}}{u^{2} + v^{2}} |)}

$z=\sqrt{1-\frac{1}{2} u^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)-\frac{1}{2} v^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)}$

Annexe: comment la formule a été dérivée

Le style classique de la narration dans les textes mathématiques consiste en l'alternance de lemmes / théorèmes et de leurs preuves - comme si les affirmations prouvables apparaissaient dans la tête des auteurs par une révélation d'en haut. Et bien qu'il y ait du vrai là-dedans, le plus souvent l'apparition des formules est précédée de quelques travaux de recherche dont la description peut donner une plus grande compréhension de leur signification que la preuve formelle; et l'exactitude des déclarations, à son tour, peut être tracée par l'exactitude des étapes qui y ont conduit.

Donc ici aussi - si l'article commençait par une formule sous une forme complexe, alors son apparence serait non évidente et contre-intuitive, et les propriétés déclarées nécessiteraient des preuves supplémentaires. Mais sous forme d'enregistrement trigonométrique, l'histoire de son apparition est tout à fait possible de retracer.

1) nous commençons par le cas le plus simple - la tâche de tracer une ligne droite en coordonnées polaires. Pour ce faire, vous devez résoudre l'équation

r \cos (ϕ) = 1

$r \cos (\phi )=1$ dont la solution est évidente

r \to \sec (ϕ)

$r\to \sec (\phi )$ ...

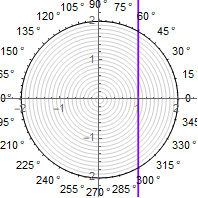
2) en outre, l'argument sécant doit être "bouclé" pour fournir des nœuds en ligne droite. C'est à ce stade que d'autres solutions utilisent un "dirty hack" sous la forme d'un reste de division. Il utilise également la prise séquentielle de la fonction sinusoïdale directe et inverse -

\sin^{- 1} (\sin (ϕ))

$\sin ^{-1}(\sin (\phi ))$

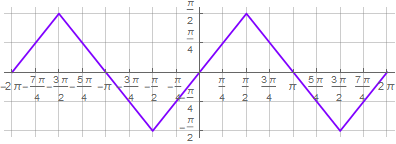
Cette approche vous permet d'effectuer des opérations mathématiques standard sur la formule résultante,

par exemple

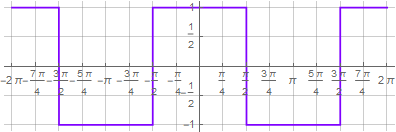
\frac{\partial \sin^{- 1} (\sin (ϕ))}{\partial ϕ} = \frac{\cos (ϕ)}{\sqrt{1 - \sin^{2} (ϕ)}}

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

Grâce à la même notation, vous pouvez simplifier la fonction carrée en coordonnées polaires pour un look plus esthétique, en utilisant la représentation complexe des fonctions trigonométriques. Dans Wolfram Mathematica, cela peut être fait en utilisant les fonctions TrigToExp et ExpToTrig:

Le code

Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify

↓

\frac{2}{\sqrt{2 + 2 \sqrt{1 - k^{2} \sin^{2} (2 ϕ)}}}

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

Grâce au même enregistrement, vous pouvez obtenir des chiffres intermédiaires lisses entre un cercle et un carré en utilisant un multiplicateur supplémentaire

k

$k$ en raison de laquelle l'argument sinusoïdal est inférieur à un -

\sin^{- 1} (k \sin (ϕ))

$\sin ^{-1}(k \sin (\phi ))$ :

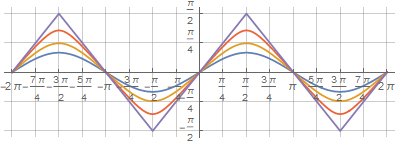
Et pour que la fonction coupe un point donné, il vous suffit de créer une équation et de recalculer

k

$k$ :

\sqrt{\frac{2}{1 + \sqrt{1 - k^{'} \sin^{2} (\frac{π}{2})}}} = k

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

Le code

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k

↓

k^{'} \to \frac{4 (k^{2} - 1)}{k^{4}}

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3) paramètres

n

$n$ et

m

$m$ ont été simplement ajoutés de manière créative et leurs effets ont été étudiés expérimentalement, en fait.

4) Le rectangle est facile à obtenir en allant dans la vue paramétrique et en "étirant" les axes

x = a \cos (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

y = b \sin (t) \sqrt{\frac{2}{1 + \sqrt{1 - \sin^{2} (2 t)}}}

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

Mais après ça

t

$t$ ne veut plus dire angle, maintenant

t

$t$ Est simplement un paramètre qui décrit un vecteur à travers ses projections sur les axes de coordonnées. Pour revenir aux coordonnées polaires, vous devez trouver la longueur du vecteur (par la racine de la somme des carrés), l'angle (par l'arc tangente du rapport), exprimer cet angle par

ϕ

$\phi$ et remplacez l'expression résultante à la place

t

$t$ ...

Le code

With[{r = Sqrt[2/(1 + Sqrt[
      

        
        
        
      

    
 1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2], 
      

        
        
        
      

    
 ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

↓

{\sqrt{2} \sqrt{\frac{a^{2} \cos^{2} (t) + b^{2} \sin^{2} (t)}{\sqrt{\cos^{2} (2 t)} + 1}}, \tan^{- 1} (\frac{b \tan (t)}{a})}

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]

↓

t \to \tan^{- 1} (\frac{a \tan (ϕ)}{b})

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])]
      

        
        
        
      

    
/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify

↓

\sqrt{2} \sqrt{\frac{a^{2} b^{2} \sec^{2} (ϕ)}{(a^{2} \tan^{2} (ϕ) + b^{2}) (\sqrt{\cos^{2} (2 \tan^{- 1} (\frac{a \tan (ϕ)}{b}))} + 1)}}

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

Simplifier une telle formule est déjà plus difficile, et cela nécessitera plusieurs étapes:

aller aux coordonnées cartésiennes en remplaçant $\phi \to \tan ^{-1}(x,y)$ ;
passer à la forme exponentielle;
simplifier;
faire un remplacement inversé $x\to \cos (\phi )$ et $y\to \sin (\phi )$ ;
revenir à la forme exponentielle;
simplifier.

En conséquence, nous obtenons la formule suivante:

Le code

Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) /
      

        
        
        
      

    
((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])
      

        
        
        
      

    
(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y] 
      

        
        
        
      

    
// TrigToExp // Simplify 
      

        
        
        
      

    
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} & 
      

        
        
        
      

    
// TrigToExp // Simplify // FullSimplify

↓

2 \sqrt{\frac{a^{2} b^{2}}{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2}) (1 + \sqrt{\frac{{((a^{2} + b^{2}) \cos (2 ϕ) - a^{2} + b^{2})}^{2}}{{((b^{2} - a^{2}) \cos (2 ϕ) + a^{2} + b^{2})}^{2}}})}}

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

Conclusion

Comme vous pouvez le voir, même dans une chose aussi simple et banale qu'un polygone, vous pouvez trouver et proposer quelque chose de nouveau. Et l'histoire ne s'arrête pas là - la formule de l'aire pour le cas général est restée inconnue, la formule d'un polygone arbitraire, et pas seulement régulier, est restée inconnue, et l'expansion en puissance et en séries trigonométriques a été laissée sans considération. Aussi, probablement, un type similaire de formule existe pour le cas tridimensionnel.

Par conséquent, si on vous dit qu'en mathématiques tout a déjà été inventé et qu'il n'y a que des problèmes qui dépassent la compréhension d'une personne ordinaire, ne le croyez pas. Il existe de nombreux problèmes purement pratiques dont les vrais mathématiciens ne sont pas conscients, ou ils ne sont pas intéressés par leur solution en raison du manque de battage publicitaire suffisant autour d'eux, ou parce qu'ils ont déjà une idée approximative des moyens de les résoudre pour leur solution. N'ayez pas peur de vous attaquer à des problèmes dont les solutions ne sont pas disponibles sur Wikipedia, n'ayez pas peur de publier leurs solutions, et n'ayez pas peur de lire les commentaires sous les articles sur l'inutilité de tout.

PS téléchargez le document original de Mathematica ici .

Comment dessiner une étoile (et plus) en coordonnées polaires

Forme complexe et modifications

Quads et trucs

Aller aux coordonnées cartésiennes

Annexe: comment la formule a été dérivée

Conclusion

More articles: