Le concepteur de mise en page n'a pas besoin de mathématiques 2: matrices, transformations de base, construction 3D et filtres pour les images

La dernière fois, nous avons parlé des graphiques et des trajectoires pour l'animation stop motion, et aujourd'hui, il s'agira de la matrice. Nous découvrirons comment créer des transformations de base en CSS, SVG et WebGL, créer un affichage du monde 3D à l'écran de nos propres mains, en traçant un parallèle avec un outil tel que Three.js, et également expérimenter avec des filtres pour les photos et comprendre ce que car une telle magie est à la base.



Permettez-moi de vous rappeler que dans cette série d'articles, nous nous familiarisons avec diverses choses du domaine des mathématiques qui effraient les concepteurs de mise en page, mais qui peuvent être utiles pour résoudre des problèmes de travail. Nous essayons d'éviter les théories inutiles, préférant les images et les explications sur les doigts, en mettant l'accent sur les applications pratiques en frontend. À cet égard, les formulations à certains endroits peuvent ne pas être tout à fait exactes du point de vue des mathématiques, ou pas tout à fait complètes. Le but de cet article est de donner une idée générale de ce qui se passe et par où commencer si quelque chose se produit.



Les scripts pour générer des images dans le style de cette série d'articles se trouvent sur GitHub , donc si vous voulez comprendre la même chose pour vous-même, vous savez quoi faire.

Peu de définitions

Une matrice en mathématiques est une telle abstraction, on peut dire que c'est un type de données dans un sens, et l'écrire sous la forme d'un tableau rectangulaire. Le nombre de colonnes et de lignes peut être n'importe quoi, mais sur le Web, nous avons presque toujours affaire à des matrices carrées 2x2, 3x3, 4x4 et 5x5.



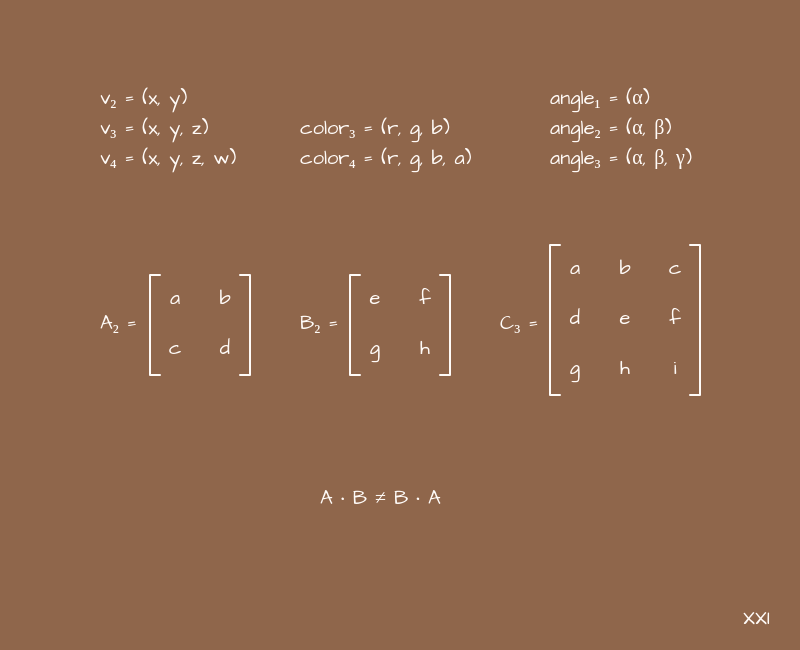
Nous avons également besoin d'une définition telle qu'un vecteur. Je pense qu'à partir de la géométrie de l'école, vous pouvez vous souvenir de la définition associée aux mots «longueur» et «direction», mais en général, en mathématiques, beaucoup de choses peuvent être appelées un vecteur. En particulier, nous parlerons d'un vecteur comme un ensemble ordonné de valeurs. Par exemple, les coordonnées de la forme (x, y) ou (x, y, z), ou une couleur au format (r, g, b) ou (h, s, l, a), etc. En fonction du nombre d'éléments inclus dans un tel ensemble, nous parlerons d'un vecteur d'une dimension ou d'une autre: si deux éléments sont bidimensionnels, trois sont tridimensionnels, etc. Aussi, dans le cadre des sujets considérés, il peut parfois être pratique de penser un vecteur comme une matrice de tailles 1x2, 1x3, 1x4, etc. Techniquement, nous pourrions nous limiter au seul terme «matrice», mais nous utiliserons toujours le mot «vecteur» pour séparer ces deux concepts l'un de l'autre,au moins dans un sens logique.



Pour les matrices, ainsi que pour les vecteurs, différentes opérations sont définies qui peuvent être effectuées avec elles. En particulier, la multiplication. Nous les multiplions constamment entre nous. L'algorithme de multiplication lui-même n'est pas très compliqué, même s'il peut sembler un peu déroutant:

function multiplyMatrices(a, b) {
    const m = new Array(a.length);

    for (let row = 0; row < a.length; row++) {
        m[row] = new Array(b[0].length);

        for (let column = 0; column < b[0].length; column++) {
            m[row][column] = 0;

            for (let i = 0; i < a[0].length; i++) {
                m[row][column] += a[row][i] * b[i][column];
            }
        }
    }

    return m;
}

Mais pour nous, en fait, il n'est pas si important de se souvenir constamment du principe de son fonctionnement lors de la résolution de problèmes quotidiens. Ici, nous le mentionnons plutôt pour être complet, pour fournir un contexte pour d'autres exemples.

Lorsque vous travaillez avec des entités complexes en mathématiques, il est très utile de faire des abstraits. Comme ici - nous parlerons souvent de multiplication, mais nous ne ferons pas attention au type d'opérations arithmétiques dans quel ordre s'y déroulent. Nous savons que la multiplication est définie - et cela suffit pour le travail.

Nous n'utiliserons que des matrices carrées dans un ensemble très spécifique de problèmes, donc un ensemble de règles simples suffira:

• Vous ne pouvez multiplier que des matrices de même dimension.
• Nous multiplions la matrice par la matrice - nous obtenons la matrice.
• Vous pouvez multiplier une matrice par un vecteur - nous obtenons un vecteur.
• L'ordre de multiplication est important.

Nous utiliserons principalement la multiplication de gauche à droite, car elle est plus familière et adaptée aux explications, mais dans certains livres ou bibliothèques, vous pouvez rencontrer une notation de droite à gauche, et toutes les matrices seront reflétées en diagonale. Cela n'affecte en aucun cas l'essence des manipulations en cours, nous ne nous attarderons donc pas là-dessus, mais si vous copiez-collez quelque chose, faites attention.

Pour les travaux ultérieurs, nous aurons également besoin d'un concept tel que la matrice d'identité. Il s'agit d'une matrice avec des uns sur la diagonale principale et des zéros dans toutes les autres cellules. L'algorithme de multiplication est construit de telle manière que multiplier la matrice d'identité par une autre matrice - nous obtenons la même matrice. Ou un vecteur, si nous parlons d'un vecteur. En d'autres termes, la matrice d'identité joue le rôle d'un dans la multiplication habituelle des nombres. C'est une chose neutre qui "n'affecte rien" lorsqu'elle est multipliée.







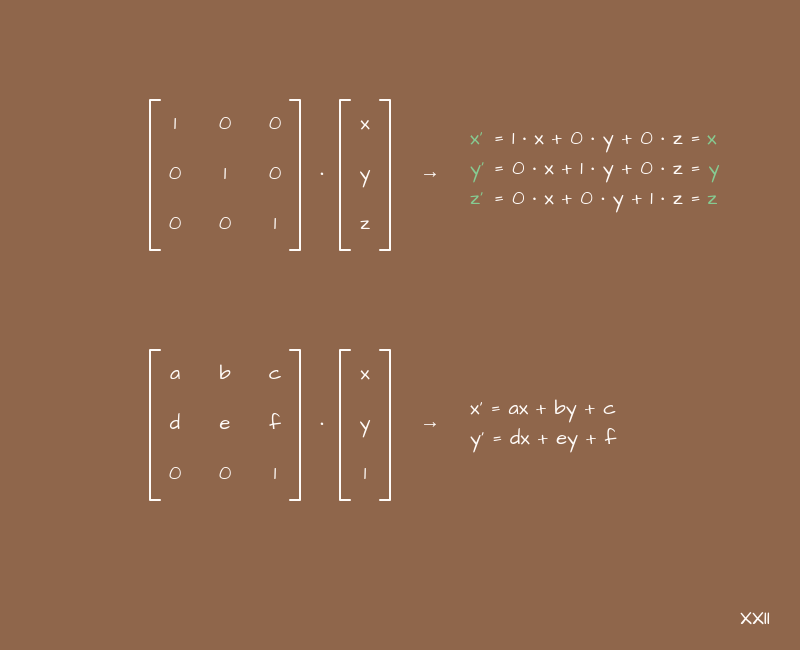
Et la dernière chose dont nous avons besoin est l'exemple montré dans l'image ci-dessus. C'est comme un cas particulier de multiplication d'une matrice par un vecteur, lorsque la dernière ligne de la matrice est "un morceau de la matrice d'identité", et le dernier élément du vecteur est également égal à 1.



Dans cet exemple, nous utilisons les lettres (x, y), et comme vous l'avez peut-être deviné, la section suivante concerne les coordonnées en 2D. Mais pourquoi ajouter une troisième coordonnée et la laisser comme une seule? - tu demandes. Tout est question de commodité ou, mieux encore, de polyvalence. Nous ajoutons très souvent +1 coordonnée pour simplifier les calculs, et travaillons avec la 2D va avec des matrices 3x3, travaillons avec 3D - avec des matrices 4x4, et travaillons avec 4D, par exemple, avec des couleurs au format (r, g, b, a) va avec des matrices 5x5. À première vue, cela semble être une idée folle, mais nous verrons plus tard comment cela unifie toutes les opérations. Si vous souhaitez comprendre ce sujet plus en détail, vous pouvez rechercher l'expression «coordonnées uniformes» sur Google.



Mais assez de théorie, passons à la pratique.

I. Transformations fondamentales de l'infographie

Prenons les expressions de l'exemple ci-dessus et voyons-les telles qu'elles sont, en dehors du contexte des matrices:

newX = a*x + b*y + c
newY = d*x + e*y + f

Vous pouvez considérer cela comme les équations paramétriques que nous avons tracées la dernière fois. Que se passe-t-il si vous définissez ces coefficients ou ces coefficients? Commençons par l'option suivante:

newX = 1*x + 0*y + 0 = x
newY = 0*x + 1*y + 0 = y

Rien ne change ici - les nouvelles coordonnées (x, y) sont identiques aux anciennes. Si nous substituons ces coefficients dans la matrice et regardons de près, nous verrons que nous obtenons la matrice d'identité.



Que se passe-t-il si nous prenons d'autres coefficients? Par exemple, ce sont:

newX = 1*x + 0*y + A = x + A
newY = 0*x + 1*y + 0 = y

Nous obtiendrons un décalage le long de l'axe X. Mais qu'aurait-il pu arriver d'autre ici? Si ce n'est pas évident pour vous, il vaut mieux revenir à la première partie, où nous avons parlé de graphiques et de coefficients.



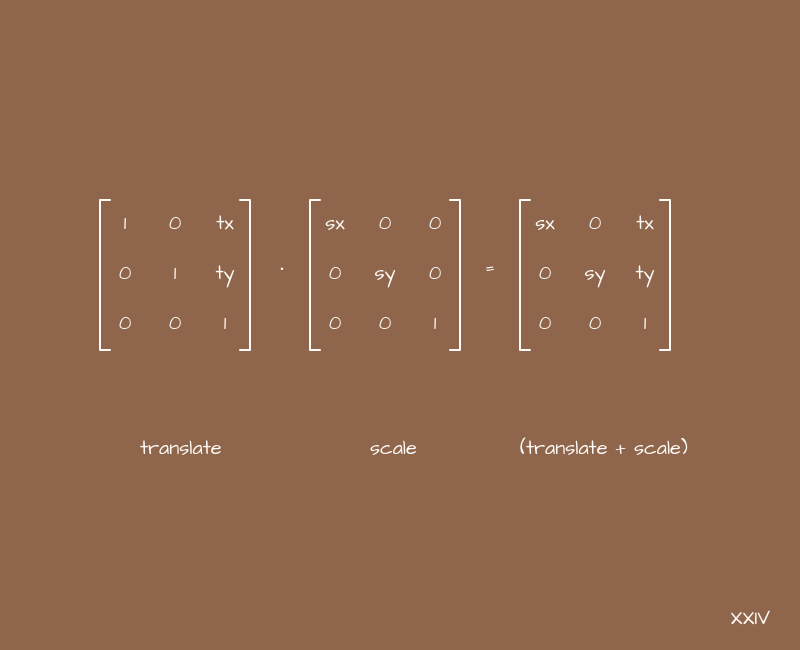
En changeant ces 6 coefficients - a, b, c, d, e, f - et en observant les changements de x et y, nous arriverons tôt ou tard à quatre de leurs combinaisons, qui semblent utiles et pratiques pour une utilisation pratique. Écrivons-les tout de suite sous forme de matrices, revenant à l'exemple d'origine:







les noms de ces matrices parlent d'eux-mêmes. Lors de la multiplication de ces matrices par des vecteurs avec les coordonnées de certains points, objets de la scène, etc. nous obtenons de nouvelles coordonnées pour eux. De plus, nous opérons avec des transformations intuitives - mouvement, mise à l'échelle, rotation et inclinaison, et les coefficients déterminent la gravité d'une transformation particulière le long des axes correspondants.

Il est souvent pratique de considérer les matrices comme des transformations pour quelque chose, comme les coordonnées. Ceci est un autre mot sur les abstractions.

Les transformations peuvent être empilées. En termes de matrices, nous utiliserons l'opération de multiplication, ce qui peut être un peu déroutant, mais c'est une surcharge de langage parlé. Si nous devons déplacer un objet sur le côté et augmenter, nous pouvons prendre une matrice pour le déplacement, une matrice pour la mise à l'échelle et les multiplier. Le résultat sera une matrice qui donne à la fois le décalage et la mise à l'échelle. Il ne reste plus qu'à transformer chaque point de notre objet avec son aide.

Transformations de base en CSS

Mais ce sont tous des mots. Voyons à quoi cela ressemble dans un vrai front-end. En CSS, nous avons (tout d'un coup) une fonction de matrice. Cela ressemble à quelque chose comme ça dans le contexte du code:

.example {
    transform: matrix(1, 0, 0, 1, 0, 0);
}

De nombreux débutants qui le voient pour la première fois sont couverts par la question - pourquoi y a-t-il six paramètres? Cela est étrange. Ça aurait été 4 ou 16 - ça ne va toujours pas où, mais 6? Que font-ils?



Mais en réalité, tout est simple. Ces six paramètres sont les coefficients mêmes à partir desquels nous venons d'assembler les matrices pour les transformations de base. Mais pour une raison quelconque, ils ont été disposés dans un ordre différent:







En CSS, il existe également une fonction matrix3d ​​afin de définir une transformation 3D à l'aide d'une matrice. Il y a déjà 16 paramètres, exactement pour faire une matrice 4x4 (n'oubliez pas que nous ajoutons +1 dimension).

Les matrices pour les transformations 3D de base sont construites de la même manière que pour la 2D, seuls plus de coefficients sont nécessaires pour les organiser non pas en deux coordonnées, mais en trois. Mais les principes sont les mêmes.

Naturellement, à chaque fois, il serait étrange de clôturer la matrice et de surveiller le placement correct des coefficients lorsque vous travaillez avec de simples transformations en CSS. Nous, les programmeurs, essayons généralement de nous faciliter la vie. Nous avons donc maintenant de courtes fonctions en CSS pour créer des transformations individuelles - translateX, translateY, scaleX, etc. Habituellement, nous les utilisons, mais il est important de comprendre qu'à l'intérieur, ils créent les mêmes matrices dont nous avons parlé, nous cachant simplement ce processus derrière une autre couche d'abstraction.



Les mêmes transformations de translation, de rotation, d'échelle et d'inclinaison, ainsi que la fonction de matrice universelle pour définir les transformations, sont présentes dans SVG. La syntaxe est légèrement différente, mais l'essence est la même. Lorsque nous travaillons avec des graphiques 3D, par exemple avec WebGL, nous aurons également recours aux mêmes transformations. Mais plus à ce sujet plus tard, il est maintenant important de comprendre qu'ils sont partout et qu'ils fonctionnent partout selon le même principe.

Sous-totaux

Résumons ce qui précède:

• Les matrices peuvent être utilisées comme transformations pour les vecteurs, en particulier pour les coordonnées de certains objets sur la page.
• Nous fonctionnons presque toujours avec des matrices carrées et ajoutons +1 dimension pour simplifier et unifier les calculs.
• Il existe 4 transformations de base: traduire, faire pivoter, mettre à l'échelle et incliner. Ils sont utilisés partout du CSS au WebGL et fonctionnent de la même manière partout.

II. Construction de scènes 3D bricolage

Un développement logique du sujet sur la transformation des coordonnées sera la construction d'une scène 3D et son affichage à l'écran. Sous une forme ou une autre, cette tâche est généralement présente dans tous les cours d'infographie, mais dans les cours frontaux, ce n'est généralement pas le cas. Nous verrons, peut-être un peu simplifié, mais néanmoins une version à part entière de la façon dont vous pouvez créer une caméra avec différents angles de vision, quelles opérations sont nécessaires pour calculer les coordonnées de tous les objets à l'écran et construire une image, et également dessiner des parallèles avec Three.js - le plus populaire outil pour travailler avec WebGL.



Une question raisonnable devrait se poser ici - pourquoi? Pourquoi apprendre à tout faire avec vos mains si vous avez un outil prêt à l'emploi? La réponse réside dans les problèmes de performances. Vous avez probablement visité des sites avec des concours comme Awwwards, CSS Design Awards, FWA, etc. Rappelez-vous à quel point les sites performants participent à ces concours? Oui, presque tout le monde ralentit, traîne lors du chargement et fait bourdonner l'ordinateur portable comme un avion! Oui, bien sûr, la raison principale est généralement des shaders complexes ou une trop grande manipulation du DOM, mais la seconde est la quantité incroyable de scripts. Cela a un effet désastreux sur le chargement de tels sites. Habituellement, tout se passe comme ceci: vous devez faire quelque chose sur WebGL - prenez une sorte de moteur 3D (+ 500 Ko) et des plugins pour cela (+ 500 Ko);vous devez faire tomber un objet ou faire voler quelque chose en morceaux - ils prennent un moteur physique (+ 1 Mo, voire plus); vous devez mettre à jour certaines données sur la page - eh bien, ajoutez un cadre SPA avec une douzaine de plugins (+ 500 Ko), etc. Et de cette façon, plusieurs mégaoctets de scripts sont tapés, qui doivent non seulement être téléchargés par le client (et ceci en plus des grandes images), mais aussi le navigateur fera quelque chose avec eux après le téléchargement - ils ne volent pas simplement vers lui. De plus, dans 99% des cas, tant que les scripts ne fonctionnent pas, l'utilisateur ne verra pas toute la beauté qu'il aurait besoin de montrer dès le début.ce que le client doit télécharger (et ceci en plus des grandes images), de sorte que le navigateur fera quelque chose avec eux après le chargement - ils ne viennent pas à lui pour une raison. De plus, dans 99% des cas, tant que les scripts ne fonctionnent pas, l'utilisateur ne verra pas toute la beauté qu'il aurait besoin de montrer dès le début.ce que le client doit télécharger (et ceci en plus des grandes images), de sorte que le navigateur en fera quelque chose après le chargement - ils ne viennent pas à lui pour une raison. De plus, dans 99% des cas, tant que les scripts ne fonctionnent pas, l'utilisateur ne verra pas toute la beauté qu'il aurait besoin de montrer dès le début.

Il est communément admis que chaque 666 Ko de scripts en production augmente le temps de chargement de la page de suffisamment de temps pour qu'un utilisateur envoie un développeur de site au prochain cercle de l'enfer. Three.js dans la configuration minimale pèse 628 Ko ...

De plus, souvent, les tâches ne nécessitent tout simplement pas la connexion d'outils complexes. Par exemple, pour afficher quelques plans avec des textures dans WebGL et ajouter quelques shaders pour faire diverger les images par vagues, vous n'avez pas besoin de tout Three.js. Et pour faire tomber un objet, vous n'avez pas besoin d'un moteur physique à part entière. Oui, cela accélérera probablement votre travail, surtout si vous le connaissez, mais vous le paierez avec le temps des utilisateurs. Ici, chacun décide par lui-même de ce qui lui est le plus profitable.

Coordonner la chaîne de transformation

En fait, l'essence des transformations de coordonnées pour construire une scène 3D sur votre écran est assez simple, mais nous allons quand même l'analyser étape par étape, car très probablement pour de nombreux concepteurs de mise en page ce processus sera quelque chose de nouveau.



Alors c'est tout. Disons qu'un concepteur a dessiné un modèle 3D. Que ce soit un cube (dans les exemples nous utiliserons les constructions les plus simples pour ne pas compliquer l'illustration à l'improviste): à







quoi ressemble ce modèle? En fait, il s'agit d'un ensemble de points dans un système de coordonnées et d'un ensemble de relations entre eux afin que vous puissiez déterminer entre quels points les plans doivent être situés. La question des avions dans le contexte de WebGL reposera sur les épaules du navigateur lui-même, et les coordonnées sont importantes pour nous. Vous devez savoir exactement comment les transformer.



Le modèle, comme nous l'avons dit, a un système de coordonnées. Mais généralement, nous voulons avoir beaucoup de modèles, nous voulons faire une scène avec eux. La scène, notre monde 3D, aura son propre système de coordonnées global. Si nous interprétons simplement les coordonnées du modèle comme des coordonnées globales, alors notre modèle sera situé comme «au centre du monde». En d'autres termes, rien ne changera. Mais nous voulons ajouter de nombreux modèles à différents endroits de notre monde, quelque chose comme ceci:







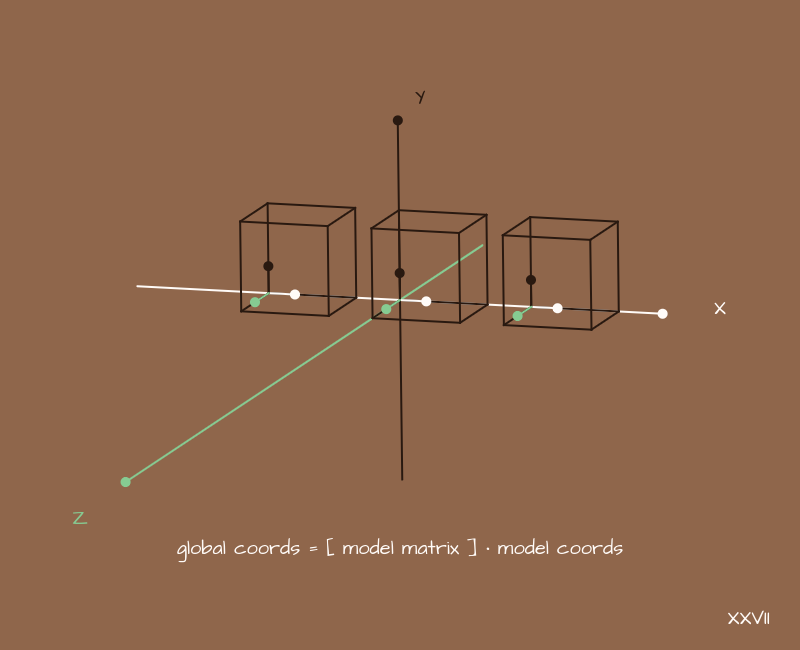
Que faire? Vous devez convertir les coordonnées de chaque modèle individuel en coordonnées globales. La position du modèle dans l'espace est définie par les décalages, les rotations et la mise à l'échelle - nous avons déjà vu ces transformations de base. Nous devons maintenant créer une matrice de transformation pour chaque modèle, qui stockera en elle-même uniquement ces informations sur l'emplacement du modèle par rapport au monde et la façon dont il est tourné.



Par exemple, pour les cubes, il y aura approximativement les matrices suivantes:

//     .
//   «  »      .
const modelMatrix1 = [
    [1, 0, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1]
];

// ,     X.
const modelMatrix2 = [
    [1, 0, 0, 1.5],
    [0, 1, 0, 0  ],
    [0, 0, 1, 0  ],
    [0, 0, 0, 1  ]
];

// ,     X   .
const modelMatrix3 = [
    [1, 0, 0, -1.5],
    [0, 1, 0, 0   ],
    [0, 0, 1, 0   ],
    [0, 0, 0, 1   ]
];

De plus, nous agirons approximativement comme suit:

    {
       = [    ] *  
}

En conséquence, chaque modèle a besoin de sa propre matrice.

De même, vous pouvez créer une chaîne de certains objets. Si un oiseau doit battre des ailes, il sera alors approprié de traduire les coordonnées des points des ailes en coordonnées de l'oiseau, puis en coordonnées mondiales globales. Il sera beaucoup plus facile de deviner immédiatement la trajectoire de l'aile en coordonnées globales. Mais il en est ainsi, au fait.

Ensuite, vous devez décider de quel côté nous allons regarder le monde. J'ai besoin d'un appareil photo.







Une caméra est une telle abstraction, comme une imitation d'une caméra physique. Il a des coordonnées et des angles d'inclinaison qui définissent son emplacement en coordonnées globales. Notre tâche est de transformer un ensemble de coordonnées désormais globales en un système de coordonnées de caméra. Le principe est le même que dans l'exemple précédent:

     {
        = [   ] *  
}

, , . !

Regardons la scène à partir de l'endroit où se trouve notre caméra conditionnelle:







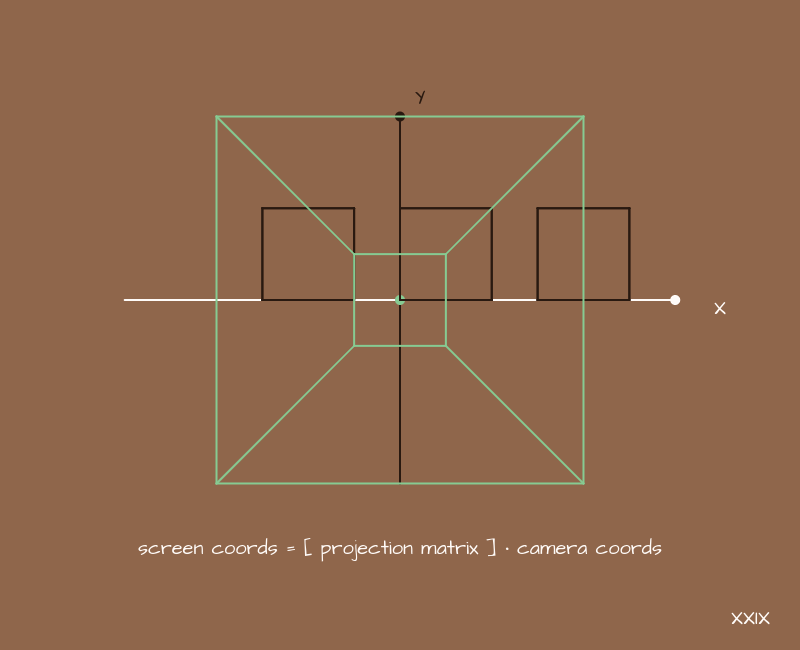
Maintenant, après avoir converti tous les points dans le système de coordonnées de la caméra, nous pouvons simplement ignorer l'axe Z et interpréter les axes X et Y comme "horizontaux" et "verticaux". Si vous dessinez tous les points des modèles sur l'écran, vous obtenez une image, comme dans l'exemple - pas de perspective et il est difficile de comprendre quelle partie de la scène tombe réellement dans le cadre. La caméra semble être de taille infinie dans toutes les directions. Nous pouvons en quelque sorte tout ajuster pour que ce dont nous avons besoin s'adapte à l'écran, mais ce serait bien d'avoir un moyen universel de déterminer quelle partie de la scène tombera dans le champ de vision de la caméra et laquelle ne le sera pas.



Avec les caméras physiques, nous pouvons parler d'une chose telle qu'un angle de vue. Pourquoi ne pas l'ajouter ici aussi?



Pour cela, nous avons besoin d'une autre matrice - la matrice de projection. En général, il peut être construit de différentes manières. En fonction de ce qui est pris comme paramètres initiaux, vous obtenez une vision légèrement différente de cette matrice même, mais l'essence sera la même. Nous prendrons la version légèrement simplifiée suivante:

//     90 
const s = 1 / (Math.tan(90 * Math.PI / 360));
const n = 0.001;
const f = 10;

const projectionMatrix  = [
    [s, 0, 0,          0],
    [0, s, 0,          0],
    [0, 0, -(f)/(f-n), -f*n/(f-n)],
    [0, 0, -1,         0]
];

La matrice de projection, d'une manière ou d'une autre, contient trois paramètres: il s'agit de l'angle de vue, ainsi que de la distance minimale et maximale aux points avec lesquels vous travaillez. Il peut être exprimé de différentes manières, il peut être utilisé de différentes manières, mais ces paramètres seront de toute façon dans cette matrice.



Je comprends qu'il n'est jamais évident pourquoi la matrice ressemble exactement à ceci, mais pour la dériver avec des explications, vous avez besoin de formules pour 2-3 pages. Cela nous ramène à nouveau à l'idée qu'il est utile d'abstraire - nous pouvons opérer avec un résultat plus général, sans entrer dans les petits détails là où il n'est pas nécessaire de résoudre un problème spécifique.



Maintenant, effectuons les transformations déjà familières:

       {
      = [   ] *   
}

Nous obtenons dans notre champ de vision exactement ce que nous attendons. En augmentant l'angle - on voit surtout sur les côtés, en diminuant l'angle - on ne voit que ce qui est le plus proche de la direction où la caméra est dirigée. PROFIT!







Mais en fait non. Nous avons oublié la perspective. Une image sans espoir est nécessaire à certains endroits, vous devez donc l'ajouter d'une manière ou d'une autre. Et ici, tout d'un coup, nous n'avons pas besoin de matrices. La tâche semble très difficile, mais elle est résolue par la division banale des coordonnées X et Y par W pour chaque point:







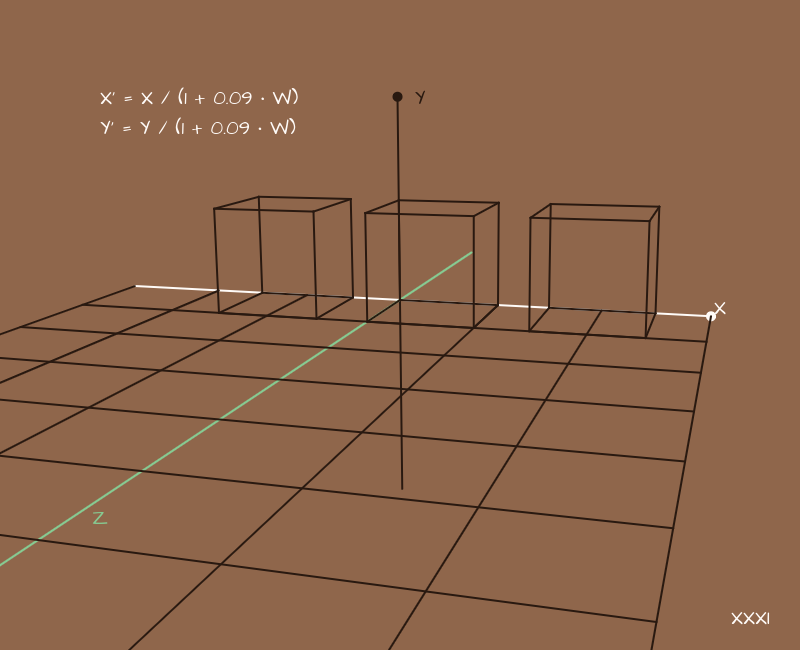
* Ici, nous avons déplacé la caméra sur le côté et ajouté des lignes parallèles "sur le sol" pour rendre plus clair où cette perspective même apparaît.

En choisissant les coefficients à notre goût, nous obtiendrons différentes options de perspective En un sens, les coefficients déterminent ici le type de lentille, dans quelle mesure elle «aplatit» l'espace environnant.

Nous avons maintenant une image complète. Vous pouvez prendre les coordonnées X et Y de chaque point et le dessiner sur l'écran comme vous le souhaitez.



En général, cela suffit pour créer une scène, mais dans de vrais projets, vous pouvez également rencontrer une transformation supplémentaire liée à la mise à l'échelle à la toute fin. L'idée est qu'après la projection, nous obtenons les coordonnées (x, y) à 1, les coordonnées normalisées, puis nous les multiplions par la taille de l'écran ou du canevas, obtenant les coordonnées à afficher sur l'écran. Cette étape supplémentaire supprime la taille du canevas de tous les calculs, ne la laissant qu'à la toute fin. C'est parfois pratique.



Ici, vous avez probablement mal à la tête à cause de la quantité d'informations, alors ralentissons et répétons toutes les transformations en un seul endroit:







Si vous combinez ces transformations en une seule, vous obtenez un petit moteur.

À quoi cela ressemble-t-il dans Three.js?

Maintenant que nous comprenons d'où vient ce petit moteur, jetons un coup d'œil à un exemple du vertex shader par défaut dans Three.js qui "ne fait rien":

void main() {
    gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
}

ou plus complètement:

void main() {
    gl_Position = projectionMatrix * viewMatrix * modelMatrix * vec4(position, 1.0);
}

Vous rappelle-t-il quelque chose? Oui, c'est ce moteur particulier. Et par "ne fait rien", nous voulons dire qu'il fait tout le travail de recalcul des coordonnées, basé sur des matrices soigneusement passées de Three.js. Mais personne ne se soucie de fabriquer ces matrices de ses propres mains, non?

Types de caméras en infographie et Three.js

Le sujet des types de caméras n'est pas directement lié aux matrices, mais nous y consacrerons tout de même quelques minutes, car nous parlons toujours de Three.js, et parfois les gens ont un désordre dans la tête à ce sujet.



La caméra est une abstraction. Cela nous aide à penser dans le monde 3D de la même manière que nous pensons dans le monde réel. Comme nous l'avons dit, une caméra a une position dans l'espace, une direction dans laquelle elle regarde et un angle de vue. Tout cela est spécifié à l'aide de deux matrices et, éventuellement, d'une division supplémentaire des coordonnées pour créer une perspective.



En infographie, nous avons deux types de caméras - «avec perspective» et «sans perspective». Ce sont deux types de caméras fondamentalement différents en termes techniques, nécessitant des actions différentes pour obtenir une image. Et c'est tout. Il n'y a rien d'autre. Tout le reste est leurs combinaisons, quelques abstractions plus complexes. Par exemple, Three.js a une caméra stéréo - ce n'est pas une sorte de caméra de "type spécial" en termes techniques, mais juste une abstraction - deux caméras légèrement espacées dans l'espace et situées à un angle:







pour chaque moitié de l'écran, nous prenons notre propre caméra et il s'avère image stéréo. Et CubeCamera, c'est 6 caméras ordinaires situées de part et d'autre d'un point, rien de plus.

Et après?

La prochaine étape, après avoir obtenu les coordonnées des objets, est de déterminer quels objets seront visibles et lesquels seront cachés derrière d'autres. Dans le contexte de WebGL, le navigateur le fera lui-même. Eh bien, il y aura aussi des tâches connexes, telles que l'imposition de textures sur celles-ci, le calcul de l'éclairage par les normales, les ombres, le post-traitement de l'image, etc. Mais nous avons déjà fait la partie la plus importante et la plus difficile à comprendre. C'est bien. En fait, de nombreuses choses génératives n'ont pas besoin de ces textures et de ces éclairages, il se peut donc très bien que les connaissances acquises maintenant soient suffisantes pour travailler avec elles.

À propos, projeter une ombre d'un objet sur un plan n'est rien de plus qu'une projection de cet objet sur ce même plan sous un certain angle, suivie d'un mélange de couleurs. Le processus est intrinsèquement très similaire à la caméra, mais il ajoute également un angle entre le plan de projection et la "direction de visualisation".

À propos des textures et des effets pour les images sur WebGL, y compris sans bibliothèques, nous en avons parlé plus d'une fois dans les articles précédents. Vous pouvez vous y référer si vous êtes intéressé par ce sujet. Ainsi, en combinant toutes ces connaissances, nous pouvons construire des objets 3D colorés à part entière de nos propres mains.

3D- . – - . , Three.js . , , , - , - . , .

Il est maintenant temps de résumer ce qui précède afin qu'il y ait de la place dans votre tête pour le prochain cas d'utilisation des matrices.



Alors:

• Vous pouvez construire un monde 3D et calculer les coordonnées des objets à l'écran de vos propres mains en utilisant un train à partir de matrices.
• Dans le monde 3D, nous fonctionnons avec une abstraction telle qu'une «caméra». Il a un emplacement, une direction et un angle de vue. Tout cela est défini en utilisant les mêmes matrices. Et il existe deux vues de base de la caméra - perspective et non perspective.
• Dans le contexte de WebGL, le rendu manuel d'une image à l'écran ou les calculs physiques peuvent souvent supprimer de lourdes dépendances et accélérer le chargement des pages. Mais il est important de trouver un équilibre entre vos scripts, les outils prêts à l'emploi et les options alternatives pour résoudre les problèmes, en faisant attention non seulement à votre commodité, mais aussi aux problèmes de vitesse de téléchargement et de performances ultimes, y compris sur les téléphones.

III. Filtres pour les images

Enfin, nous examinerons un tel domaine d'application des matrices en tant que filtres pour les images. Si nous considérons une couleur au format RGBA comme un vecteur, alors nous pouvons supposer qu'ici nous pouvons appliquer une transformation similaire à celle que nous avons utilisée avec les coordonnées:







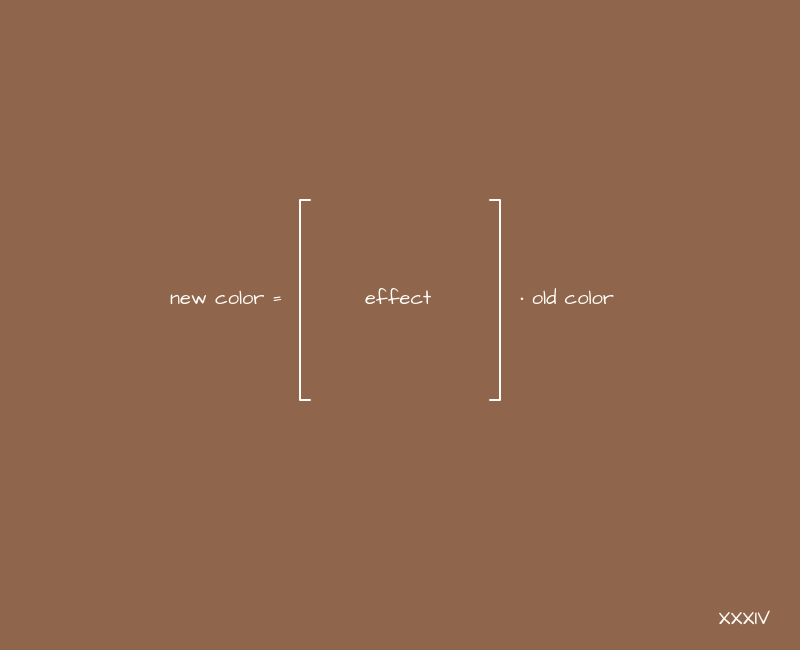
Et l'appliquer à l'image selon le principe évident:

    {
       = [  ] *   
}

Si la matrice d'identité agit comme une matrice, rien ne changera, nous le savons déjà. Que se passe-t-il si vous appliquez des filtres similaires pour traduire et mettre à l'échelle des transformations?







OU. Le résultat est des filtres de luminosité et de contraste. Intéressant.

Lorsque vous expérimentez avec de tels filtres, vous devez toujours vous rappeler d'ajuster les valeurs afin que l'image ne soit pas surexposée. Si vous multipliez quelque chose par un grand nombre, vous devrez probablement soustraire ou diviser quelque chose quelque part. Comme indiqué dans l'exemple précédent.

Comment faire une image en noir et blanc à partir d'une image en couleur? La première chose qui peut venir à l'esprit est d'ajouter les valeurs des canaux RVB, de les diviser par 3 et d'utiliser la valeur résultante pour les trois canaux. En format matriciel, cela ressemblera à ceci:







Et bien que nous ayons obtenu une image en noir et blanc, elle peut encore être améliorée. Notre œil perçoit en fait différemment la légèreté des différentes couleurs. Et afin de transmettre cela pendant la désaturation, nous créons des coefficients différents pour chaque canal RVB de cette matrice.



L'exemple ci-dessous présentera les valeurs généralement acceptées pour ces coefficients, mais personne ne prend la peine de jouer avec eux. Au total, ces coefficients devraient donner 1, mais en fonction de leurs proportions, nous obtiendrons des images en noir et blanc légèrement différentes. Cela peut, dans une certaine mesure, simuler un rendu des couleurs différent lorsque vous travaillez avec des caméras argentiques.



Et si nous multiplions également un peu la diagonale principale, nous obtenons un filtre de saturation universel:







il fonctionne dans les deux sens - à la fois en désaturation (vous pouvez atteindre une image complètement en noir et blanc) et en saturation. Tout dépend du coefficient correspondant.



En général, vous pouvez jouer avec des filtres pendant une longue période, en obtenant une variété de résultats:







* Les matrices utilisées dans cet exemple peuvent être visualisées sur GitHubsi vous en avez soudainement besoin. Pour être insérés dans l'article, leur volume sera excessif.



Mais prêtons toujours un peu d'attention à l'endroit où cela s'applique réellement. Il est clair que l'idée même de remplacer la couleur de chaque pixel suggère des shaders pour traiter une photo, ou pour post-traiter une scène 3D, mais peut-être est-ce encore quelque part dans le frontend?

Filtres en CSS

En CSS, nous avons une propriété de filtre. Et là, en particulier, il existe de telles options pour les filtres liés aux couleurs:

• luminosité (nous l'avons fait)
• contraste (terminé)
• inverser (identique au contraste, seuls les principaux coefficients diagonaux avec un signe différent)
• saturer (terminé)
• niveaux de gris (comme déjà noté, il s'agit d'un cas particulier de saturation)
• sépia (un concept très vague, différentes versions de sépia sont obtenues en jouant avec des coefficients, où l'on réduit en quelque sorte la présence de bleu)

Et ces filtres acceptent des coefficients en entrée, qui sont ensuite substitués sous une forme ou une autre dans les matrices que nous avons faites précédemment. Nous savons maintenant comment cette magie fonctionne de l'intérieur. Et maintenant, il est clair comment ces filtres sont combinés dans les entrailles de l'interpréteur CSS, car tout ici est construit selon le même principe qu'avec les coordonnées: multiplier les matrices - ajouter des effets. Certes, il n'y a pas de matrice de fonction personnalisée dans cette propriété en CSS. Mais c'est en SVG!

Filtrer les matrices en SVG

Dans SVG, nous avons feColorMatrix, qui est utilisé pour créer des filtres pour les images. Et ici, nous avons déjà une liberté totale - nous pouvons faire une matrice à notre goût. La syntaxe est quelque chose comme ceci:

<filter id=’my-color-filter’>
    <feColorMatrix in=’SourceGraphics’
        type=’matrix’,
        values=’1 0 0 0 0
                0 1 0 0 0
                0 0 1 0 0
                0 0 0 1 0
                0 0 0 0 1‘
    />
</filter>

Vous pouvez également appliquer des filtres SVG à des éléments DOM normaux dans CSS, il y a une fonction url spéciale pour cela ... Mais je ne vous l'ai pas dit!

En fait, les filtres SVG dans CSS ne sont toujours pas pris en charge par tous les navigateurs (ne pointant pas du doigt IE), mais il y a des rumeurs selon lesquelles Edge passe enfin à un moteur chrome, et les anciennes versions perdront le support dans un avenir prévisible, il est donc temps d'utiliser cette technologie. maître, vous pouvez faire beaucoup de choses intéressantes avec.

Que se passe-t-il d'autre?

En plus des effets pour les images, construits sur le principe des transformations, il existe diverses choses construites sur des déplacements de pixels, mélangeant leurs couleurs et d'autres manipulations, où la matrice peut être un bon format pour stocker des données par lesquelles cette manipulation même devrait avoir lieu.

Matrice du noyau

En particulier, dans le frontend, nous rencontrons une chose telle que la matrice du noyau et ses effets associés. Le point est simple: il existe une matrice carrée, généralement 3x3 ou 5x5, bien qu'il puisse y en avoir plus, et les coefficients y sont stockés. Au centre de la matrice - pour le pixel "courant", autour du centre - pour les pixels voisins. Si la matrice est 5x5, un autre calque apparaît autour du centre - pour les pixels situés à un de celui actuel. Si 7x7 - alors une autre couche, etc. En d'autres termes, nous considérons la matrice comme un champ bidimensionnel, sur lequel vous pouvez organiser les coefficients à votre discrétion, déjà sans référence à aucune équation. Et ils seront interprétés comme suit:

    {
       =
           ,      
}

Une toile vierge n'est pas très adaptée à de telles tâches, mais les shaders sont très uniformes. Mais il est facile de deviner que plus la matrice est grande, plus nous utiliserons de pixels voisins. Si la matrice est 3x3, nous ajouterons 9 couleurs, si 5x5 - 25, si 7x7 - 49, etc. Plus d'opérations - plus de charge sur le processeur ou la carte vidéo. Cela affectera inévitablement les performances de la page dans son ensemble.

Dans la mesure du possible, utilisez de petites matrices pour ces effets si vous avez besoin de les superposer quelque part en temps réel.

Dans SVG, nous avons une balise spéciale feConvolveMatrix, qui est conçue uniquement pour créer de tels effets:

<filter id=’my-image-filter’>
    <feConvolveMatrix
        kernelMatrix=’0 0 0
                      0 1 0
                      0 0 0’
    />
</filter>

Ici, nous avons créé le filtre le plus simple pour l'image, qui ne fait rien - la nouvelle couleur pour chaque pixel sera égale à la couleur actuelle multipliée par 1 et les valeurs des couleurs des pixels voisins seront multipliées par 0.

Notez que différents navigateurs rendent les SVG différemment et que le rendu des couleurs peut également flotter très largement. Parfois, la différence est tout simplement catastrophique. Alors testez toujours vos filtres SVG ou utilisez un canevas, ce qui est plus prévisible dans notre contexte.

Si nous commençons à organiser les nombres en couches, du plus grand au plus petit, nous obtenons un flou:







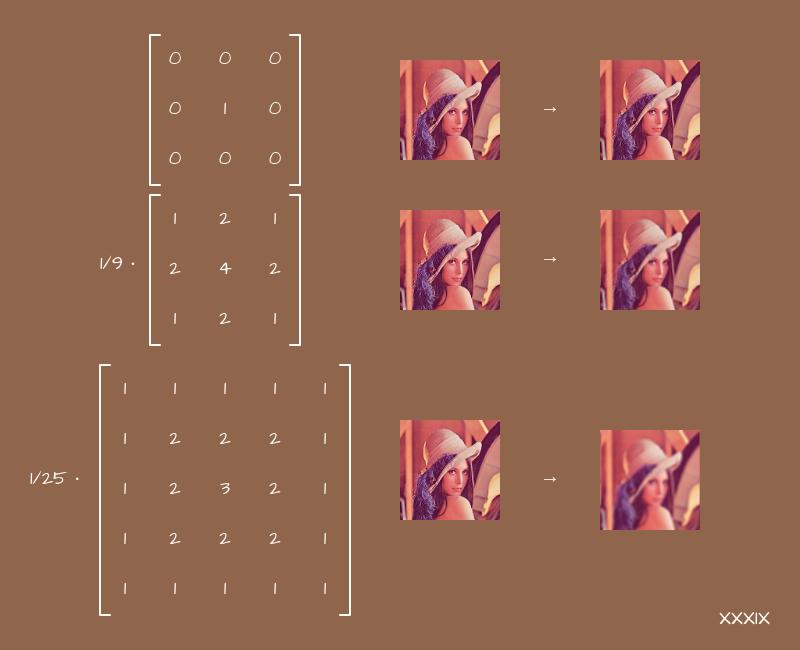
plus la matrice est grande, plus nous touchons de pixels voisins, plus l'image est lavée. L'essentiel ici est de ne pas oublier de normaliser les valeurs, sinon l'image s'allumera simplement.

Maintenant, sachant comment fonctionne le flou, nous pouvons comprendre pourquoi son utilisation active sur une page dans CSS ou SVG conduit à des freins - pour chaque pixel, le navigateur effectue un tas de calculs.

Si vous commencez à expérimenter la modification des signes des coefficients et à les organiser dans différents modèles, vous obtiendrez des effets d'accentuation, une détection des contours et quelques autres. Essayez de jouer avec eux vous-même. Cela pourrait être utile.







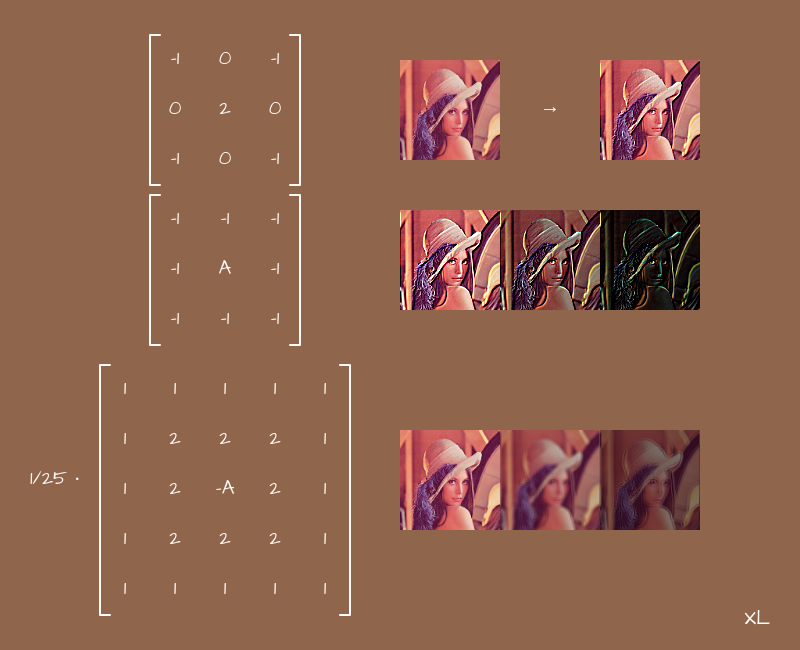
Ainsi, vous pouvez créer différents effets pour les photos, voire la vidéo, en temps réel, et les rendre dépendants d'une action de l'utilisateur. Tout dépend de votre imagination.

Sous-totaux

Résumons ce qui a été dit dans cette partie:

• Les matrices peuvent être utilisées non seulement pour les transformations liées aux coordonnées, mais également pour créer des filtres de couleur. Tout est fait selon le même principe.
• Les matrices peuvent être utilisées comme un stockage 2D pratique pour certaines données, y compris différents coefficients pour les effets visuels.

Conclusion

Si nous nous abstenons un peu des algorithmes compliqués, les matrices deviendront un outil abordable pour résoudre des problèmes pratiques. Avec leur aide, vous pouvez calculer de vos propres mains les transformations géométriques, y compris dans le cadre de CSS et SVG, construire des scènes 3D, et également réaliser toutes sortes de filtres pour les photos ou pour le post-traitement d'images dans le cadre de WebGL. Tous ces sujets vont généralement au-delà du frontend classique et sont plus liés à l'infographie en général, mais même si vous ne résolvez pas ces problèmes directement, connaître les principes pour les résoudre vous permettra de mieux comprendre le fonctionnement de certains de vos outils. Ce ne sera jamais superflu.



J'espère que cet article vous a aidé à comprendre le sujet de l'application pratique des matrices dans le frontend, ou du moins vous a donné une base à partir de laquelle vous pouvez vous appuyer dans votre développement ultérieur. Si vous pensez que certains autres sujets liés aux mathématiques ou à la physique méritent le même examen dans le contexte de la mise en page, écrivez vos réflexions dans les commentaires, peut-être que l'un des prochains articles en discutera.