À la mention de l'expression «éponge de mer», quelqu'un peut avoir une image d'un personnage de dessin animé extrêmement populaire dans sa tête. Cependant, le meilleur employé Krusty Krab n'a rien à voir avec son vrai prototype. Visuellement, différents types d'éponges de mer sont différents: amphores grecques anciennes, instruments à vent complexes, branches d'arbres séchées, fleurs fantaisie, etc. Mais derrière l'apparence extérieure se cache une structure cellulaire incroyablement complexe qui attire l'attention de la communauté scientifique depuis plusieurs années maintenant. Des chercheurs de l'Université de Harvard ont récemment découvert que les caractéristiques structurelles des éponges marines peuvent servir d'inspiration pour des gratte-ciel plus forts et plus hauts, des ponts plus longs et des vaisseaux spatiaux ultralégers. Pourquoi la structure de l'éponge de mer est-elle unique,quelles sont ses caractéristiques mécaniques et quels résultats ont montré les prototypes basés sur les données obtenues? Nous trouverons des réponses à ces questions dans le rapport des scientifiques. Aller.
Base de recherche
Il existe environ 8000 espèces d'éponges de mer dans le monde, mais cette étude se concentre sur les éponges à six rayons ( Hexactinellida ). Ce type d'éponge est également très diversifié, avec environ 600 espèces. Ils vivent dans les mers à des profondeurs de 5 à plus de 6000 mètres.
Les éponges à six rayons tirent leur nom de la structure de leur squelette, composé d'aiguilles en silicium à six rayons, situées dans trois plans mutuellement perpendiculaires.
La forme du corps de Hexactinellida peut être très différente: tubulaire, gobelet, grumeleuse, processeuse, lobée, etc. Malgré les différences visuelles, la composition corporelle de toutes les espèces est assez similaire. La base du corps est un seul syncytium * .
* — , .Un diagramme à lui seul suffit pour comprendre pourquoi une éponge de verre peut être si utile dans l'architecture ou la construction de ponts.
(Hexactinellida): — ; - — ; — ; — .
Dans cette étude, les scientifiques ont examiné le système squelettique minéralisé de l'éponge Euplectella aspergillum (panier de fleurs de Vénus), qui a une architecture hiérarchique unique et une résistance mécanique sur de nombreuses échelles de longueur.

Euplectella aspergillum (vue de dessus).
Éléments du squelette vitreuses (spicules) E. goupillon composée d'un noyau de protéine centrale entourée par une alternance de couches concentriques de nanoparticules de silice consolidé (silice, SiO 2) et de fines couches organiques. Les spicules sont organisés pour former une grille carrée, renforcée par deux ensembles entrecroisés d'entretoises diagonales appariées, créant un motif en damier d'alternance de cellules ouvertes et fermées.
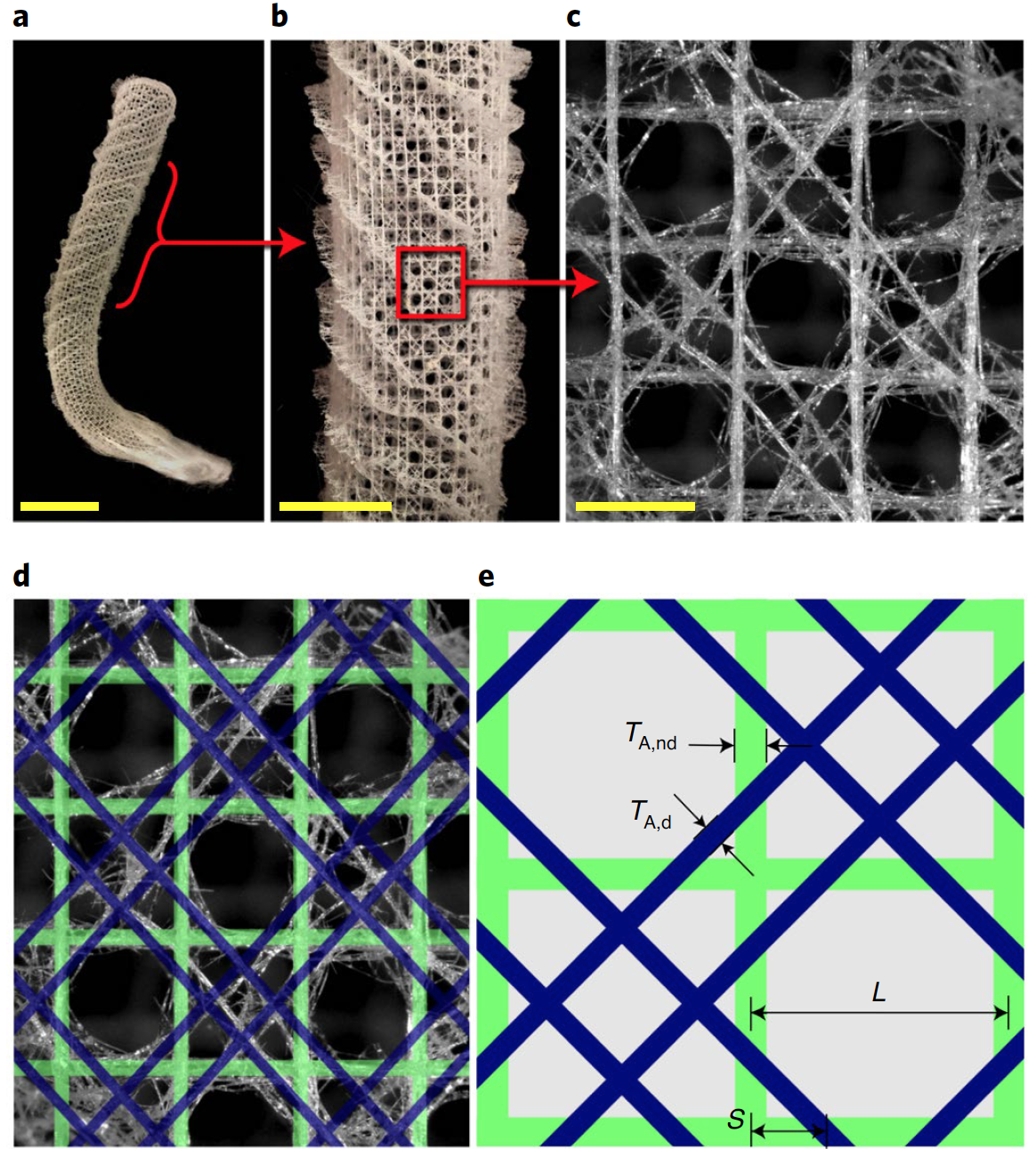
Image # 1
Auparavant, l'effet de l'architecture de spicules multicouches sur le ralentissement de la propagation des fissures et l'augmentation de la résistance à la flexion a été considéré, mais les avantages mécaniques potentiels d'un réseau carré à deux diagonales de spicules n'ont pas reçu beaucoup d'attention.
Les scientifiques rappellent que les réseaux à cellules ouvertes comme ceux trouvés dans le système squelettique d' E. Aspergillumsont couramment utilisés dans un contexte d'ingénierie en raison de leur poids plus léger, de leur forte absorption d'énergie et de leur capacité à contrôler la propagation des ondes acoustiques et de chaleur. En règle générale, les propriétés et la fonctionnalité de ces formes géométriques dépendent du type et des caractéristiques de la connexion de leurs nœuds (points d'intersection).
Par exemple, un nombre minimum de nœuds de six est requis pour les réseaux bidimensionnels dans lesquels la tension prédomine, ce qui permet d'obtenir un rapport résistance / poids plus élevé pour les applications structurelles. Mais les treillis à géométrie carrée simple (avec une connexion de nœud de quatre) sont plutôt instables lorsque le vecteur de charge a une composante transversale, de sorte qu'une connexion diagonale est nécessaire pour la stabilisation.
Dans le travail que nous envisageons aujourd'hui, les scientifiques ont utilisé le squelette d'E. Aspergillum comme base pour créer des architectures en treillis carrés mécaniquement robustes. Au cours de l'étude, des méthodes d'analyse expérimentale et numérique ont été utilisées pour déterminer les propriétés mécaniques du réseau squelettique de l'éponge.
Résultats de recherche
Pour mieux comprendre les avantages mécaniques de l'architecture squelettique de l'éponge, une comparaison a été faite de ses caractéristiques géométriques avec celles de trois autres réseaux bidimensionnels à base carrée (tous les quatre avaient le même volume, c'est-à-dire la même quantité de matière).
Dans chacune de ces structures, l'architecture carrée de base était constituée d'éléments de longueur L et de section rectangulaire caractérisés par une profondeur H suffisamment grande pour éviter une déformation hors plan.
L'option A, inspirée d'une éponge de mer, se composait d'éléments horizontaux et verticaux (hors diagonale) d'épaisseur T A, nd = 0,1 L et de deux ensembles de doubles diagonales parallèles d'épaisseur T A, d= 0,05 L situé à une distance S = L / (√2 + 2) des nœuds ( 2à ).

Image # 2 L'
option B était également basée sur l'architecture d'éponge avec T B, nd = 0,1 L, mais ne contenait qu'une seule diagonale d'épaisseur T B, d = 0,1 L, traversant chacune des cellules fermées ( 2b ).
L'option C (T C, nd = 0,1 L) était basée sur l'architecture utilisée dans les applications d'ingénierie modernes, avait un ensemble de poutres diagonales croisées d'épaisseur T C, d = 0,05 L dans chaque cellule ( 2c ).
L'option D n'avait pas de renforcement diagonal et ses éléments horizontaux et verticaux étaient T D, nd = 0,1L (1 + 1 / √2) (2d ).
Tout d'abord, la réponse mécanique sous compression uniaxiale le long des éléments verticaux des quatre options de réseau décrites ci-dessus a été analysée.
Des échantillons contenant des mosaïques 6x6 de cellules carrées avec L = 1,5 cm et H = 4 cm ont été réalisés sur une imprimante 3D Connex500 (Stratasys). La compression uniaxiale a été réalisée à l'aide d'un appareil Instron (modèle 5969) avec une cellule de pesée de 50 kN ( 2e ).
Sur le graphique 2fmontre les courbes contrainte-déformation à partir desquelles deux conclusions principales peuvent être tirées. Premièrement, toutes les conceptions de renforcement diagonales (options A, B et C) avaient une réponse élastique initiale presque identique, ce qui démontre que différentes conceptions de renforcement diagonales n'affectaient pas la rigidité globale initiale de la structure. L'option D, comme prévu, a montré une rigidité initiale plus élevée en raison des éléments verticaux et horizontaux plus épais.
Deuxièmement, toutes les courbes montrent une capacité de charge maximale claire, la structure A (variante inspirée de l'éponge) prenant la charge la plus élevée.
Étant donné que chaque charge maximale correspond au début du flambement, les scientifiques ont conclu que la conception A présentait la contrainte de flambement critique la plus élevée de toutes les options de flambement considérées.
De plus, il a été constaté que dans les trois structures à diagonales, la dynamique après perte de stabilité conduisait à une transformation homogène de la structure dans tout l'échantillon ( 2e ).
Mais dans la variante D, le mode critique conduit à une longueur d'onde beaucoup plus longue que la taille de la cellule carrée, ce qui, après perte de stabilité, conduit à la formation d'une forme qualitativement similaire à celle d'un faisceau courbe compressé.
Pour comprendre comment la conception du treillis inspirée de l'éponge a abouti à des améliorations significatives des performances mécaniques, la modélisation par éléments finis a été réalisée à l'aide du logiciel ABAQUS / Standard.
Pour la modélisation, la géométrie a été construite à l'aide d'éléments de poutre Timoshenko (élément de type ABAQUS B22), et la réaction du matériau a été enregistrée à l'aide d'un modèle de matériau incompressible avec un module de cisaillement μ = 14,5 MPa.
Le processus de modélisation s'est déroulé en trois étapes:
- analyse de flambement;
- puis une perturbation a été appliquée aux nœuds du maillage sous la forme du mode de flambement le plus bas;
- analyse non linéaire statique pour évaluer les réponses non linéaires aux grandes déformations.
Le graphique 2f montre une concordance très étroite entre les résultats numériques et expérimentaux.
De plus, le modèle d'éléments finis a été intentionnellement étendu pour étudier l'influence de la direction de la charge. Afin de réduire les coûts de calcul et d'éliminer les effets de bord, la périodicité des structures a été utilisée et la réponse des éléments de volume représentatifs (RVE) avec des conditions aux limites périodiques appropriées a été étudiée.
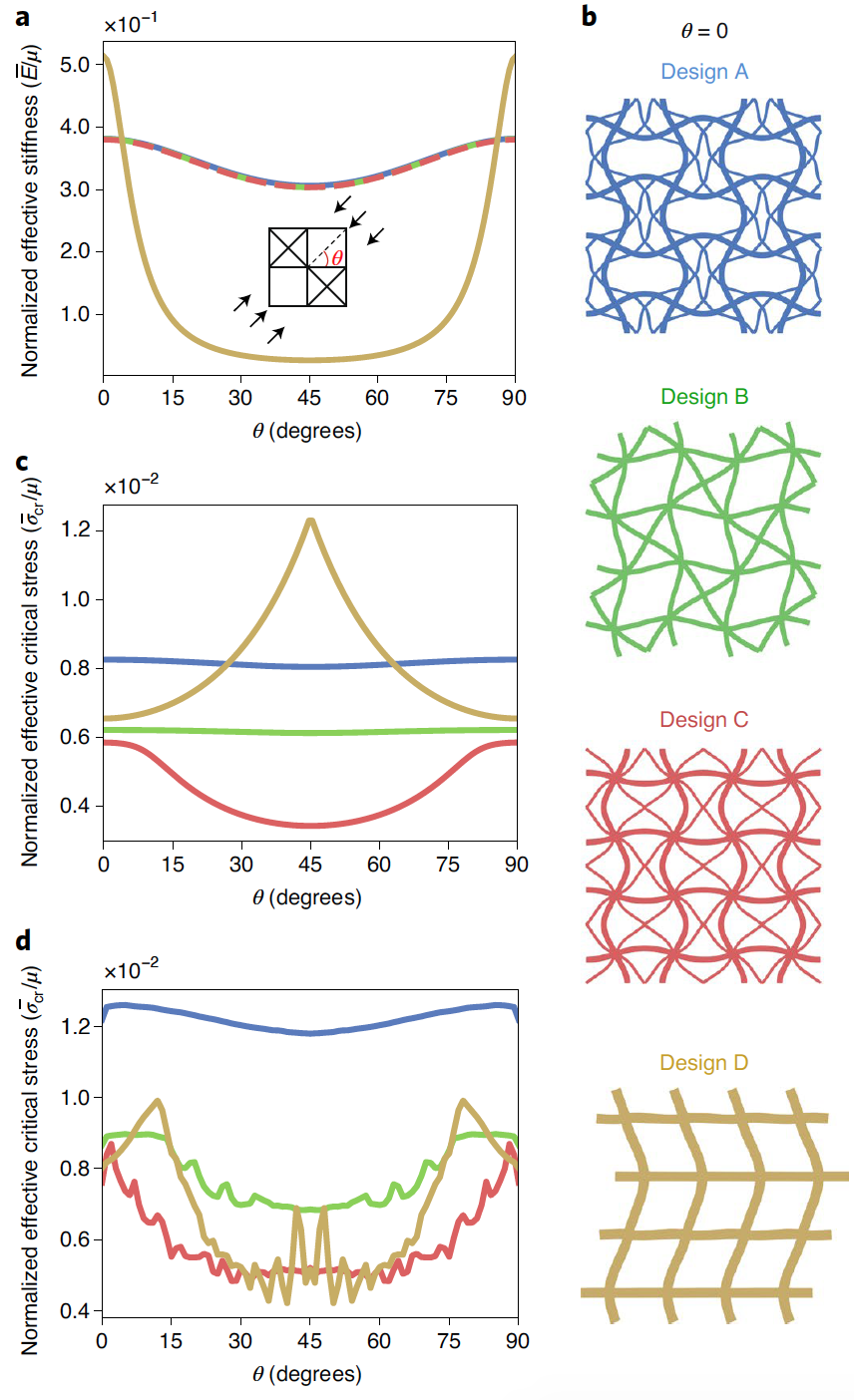
Image n ° 3
à 3amontre l'évolution de la rigidité structurelle effective (E) en fonction de l'angle de charge (θ). Il a été constaté que la rigidité de toutes les structures contenant un renforcement diagonal était pratiquement la même quel que soit l'angle de charge. Ce fait confirme en outre que la rigidité de la structure était principalement déterminée par la quantité de matière distribuée le long de la direction de la charge.
En conséquence, la structure D, dans laquelle tout le matériau était classé comme éléments hors diagonale, présentait la rigidité la plus élevée à θ = 0 °, mais avait une capacité portante négligeable à θ = 45 °.
De plus, l'influence de θ sur les caractéristiques de flambement des structures A - D a été étudiée. Contrainte de flexion critique effective (̅σ cr) de la conception A était plus élevée que celle des autres conceptions d'armatures diagonales (conceptions B et C) pour toutes les valeurs de θ ( 3b ). La construction D surpasse la construction A dans l'intervalle 27 ° <θ <63 °, en supposant que ces constructions sont infinies. Cependant, étant donné le comportement de flambement global de la structure D, ces caractéristiques ont été largement influencées par les effets de limite et la contrainte de flambement critique a été considérablement réduite lorsque l'on considère une structure avec une RVE 10x10 bien dimensionnée ( 3d ). De plus, la géométrie de la structure A a conservé sa robustesse même après des modifications du réseau en introduisant différents niveaux de désordre, ce qui est cohérent avec les caractéristiques observées dans le squelette de l'éponge marine.
La simulation ci-dessus et les résultats des tests réels montrent clairement que l'option de conception A, basée sur le squelette d'une éponge de mer, surpasse clairement ses concurrents (options B, C et D). Cependant, les tests n'ont pas été terminés à ce sujet, car les scientifiques se sont demandé s'il était possible de créer une structure qui serait encore meilleure.
A cette fin, un problème d'optimisation a été formulé visant à déterminer le nombre (N) d'éléments diagonaux d'un réseau carré, ce qui permettrait d'obtenir une contrainte de flexion critique plus élevée. Il était également nécessaire d'établir la distance entre ces éléments et les nœuds des joints de réseau S i (où i = 1, 2, ..., N), ainsi que le rapport des éléments diagonaux et hors diagonaux λ = V nd / V d (Vnd et V d sont respectivement les volumes des éléments hors diagonale et diagonale). Toutes ces variables affectent d'une manière ou d'une autre les indicateurs de contrainte de flexion.
Lors des tests, des structures RVE 3x3 ont été soumises à une compression uniaxiale parallèle aux éléments hors diagonale (θ = 0 °). La fonction objective Z = ̅σ cr a été maximisée en utilisant une modélisation par éléments finis couplée à une implémentation Python de l'algorithme d'évolution d'adaptation de matrice de covariance (CMA-ES). Pour chaque jeu de données d'entrée défini par le CMA-ES, une analyse de flambement par éléments finis a été effectuée pour obtenir ̅σ cr , qui a ensuite été utilisée pour estimer la fonction objectif Z.
Sept optimisations différentes ont été effectuées, dont chacune considérait un nombre entier fixe d'éléments diagonaux N compris entre un et sept (N = ℤ ϵ [1, 7]). Pour assurer la symétrie du système, les règles suivantes ont été prises en compte: S 2i - 1 = S 2i (i = 1, 2, ..., N / 2), si N est un nombre pair; S 1 = 0 et S 2i - 1 = S 2i (i = 2, 3, ..., (N - 1) / 2) si N est impair.
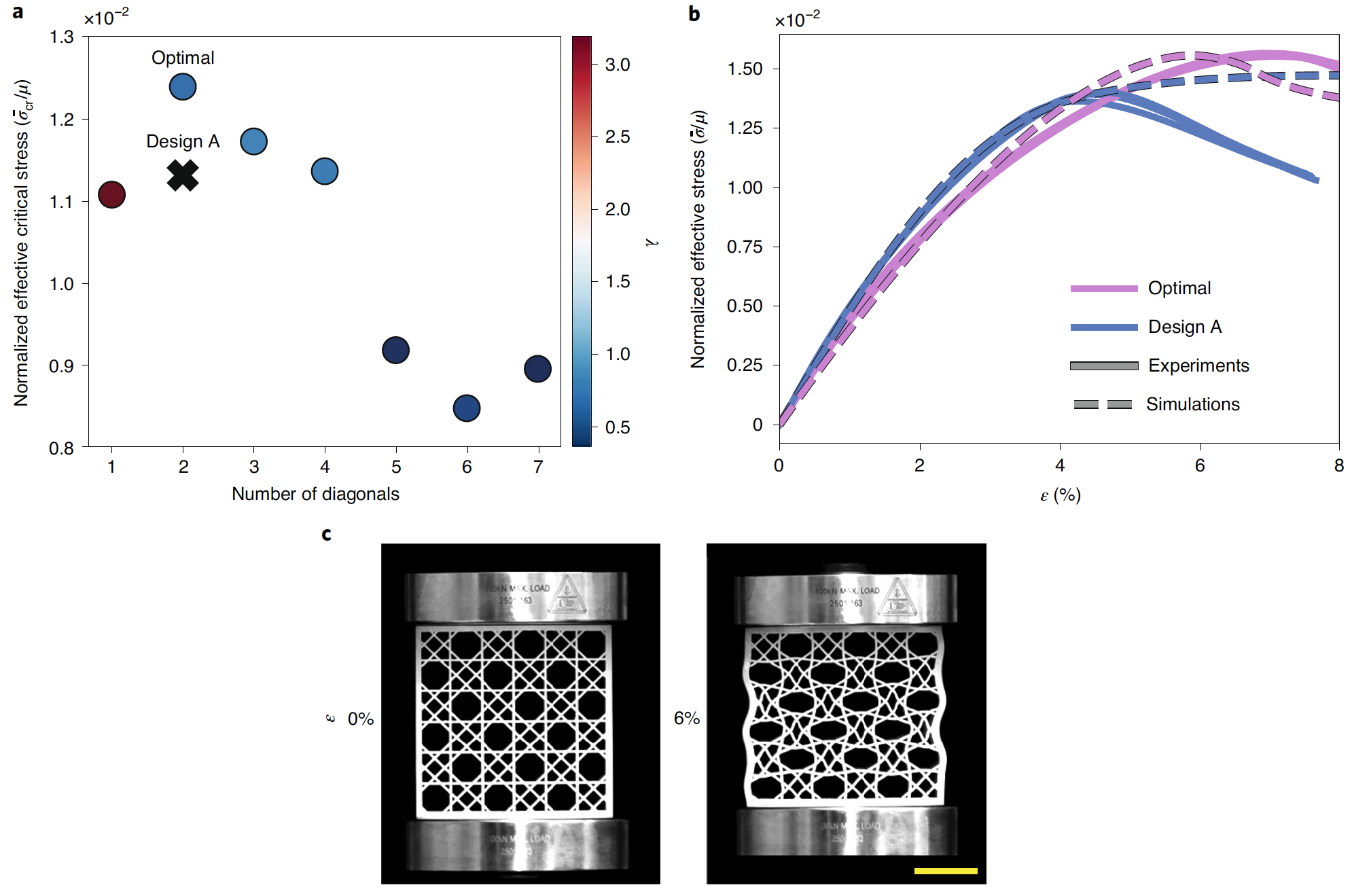
Image №4 Le
graphique 4a montre la valeur la plus élevée ̅σ cr , certains modèles CMA-ES pour toutes les valeurs considérées N. On a constaté que la valeur la plus élevée ̅σ crn'était que de 9,55% plus élevé que dans le cas de la conception A précédemment testée. 0,6778). Les résultats de la simulation ont été confirmés expérimentalement avec succès ( 4b ).
Les scientifiques notent que la structure squelettique de l'éponge marine E. aspergillum est une grande source d'inspiration pour plus que de simples architectures en treillis (construction A). Pour le démontrer, l'image 5a montre une fine mosaïque à mailles carrées de 11x2 soumise à une contrainte de flexion en trois points.
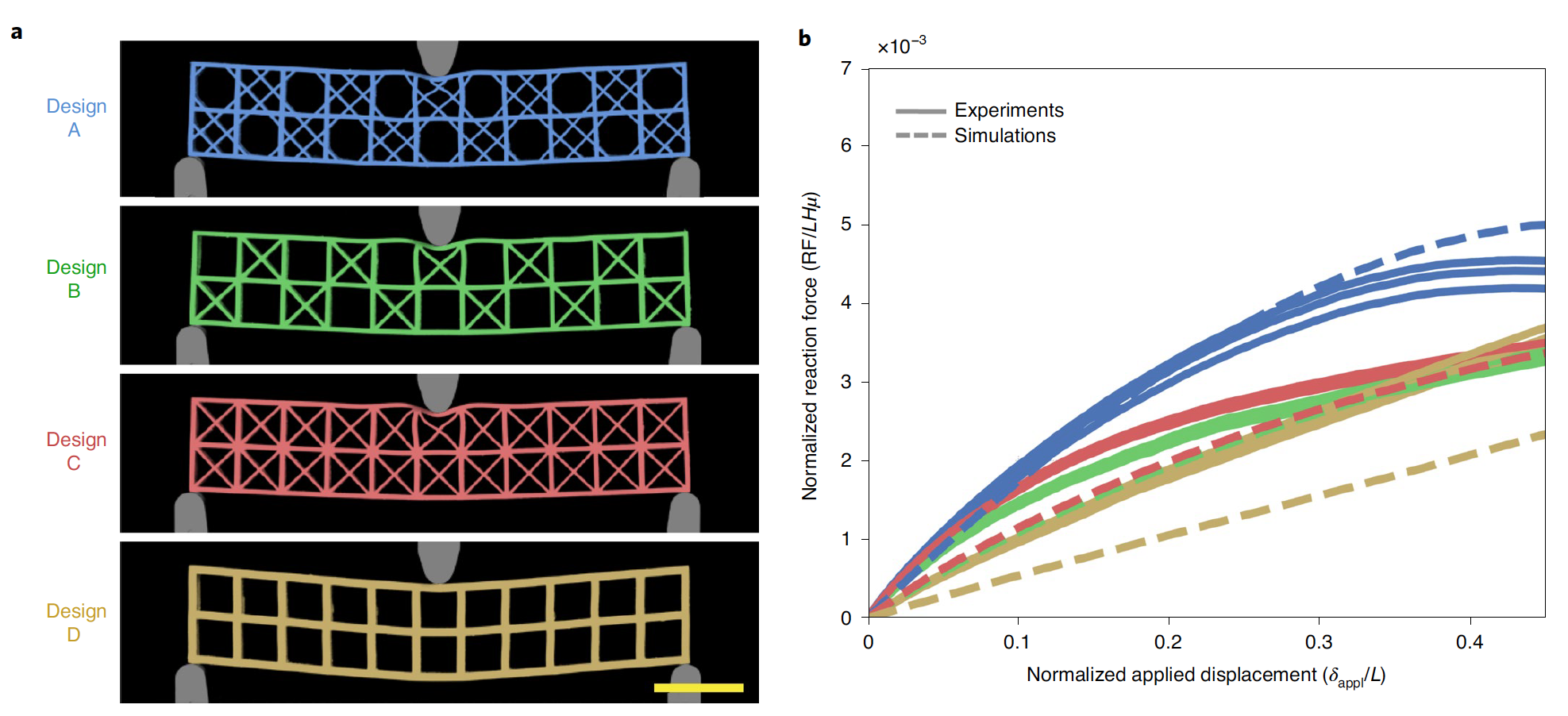
Image # 5
Comme expériences ( 5b) et des simulations d'éléments finis ont démontré que la conception inspirée de l'éponge était plus rigide et pouvait supporter des charges 15% plus élevées sur une plus large gamme de déplacements appliqués.
Pour une connaissance plus détaillée des nuances de l'étude, je vous recommande de consulter le rapport des scientifiques et des éléments supplémentaires .
Épilogue
La nature a toujours été, est et sera l'une des principales sources d'inspiration de la recherche scientifique. Dans ce travail, cette affirmation a été confirmée par l'exemple des éponges de mer de l'espèce Euplectella aspergillum, dont la structure squelettique présente des caractéristiques étonnantes. La principale caractéristique est que cette structure biologique est capable de résister à des charges importantes, alors qu'une quantité minimale de matériau est impliquée dans sa construction. En d'autres termes, les éponges de mer sont assez poreuses (en gros), mais très durables.
L'étude a montré que l'architecture du squelette d'une éponge de mer peut être extrêmement utile dans divers domaines de l'activité humaine. L'introduction de l'architecture en éponge dans la construction permettra la création de gratte-ciel plus hauts et de ponts plus longs, tandis que la quantité optimale de matériau sera dépensée et que la résistance des structures finies ne sera pas affectée. Cette technique peut également être utilisée dans la construction aéronautique, la construction navale et même dans l'astronautique, car minimiser la masse du navire minimisera la consommation de carburant.
Vendredi off-top:
Euplectella aspergillum ( , EV Nautilus 2014 ).
Euplectella aspergillum ( , EV Nautilus 2014 ).
Merci pour votre attention, restez curieux et passez un super week-end les gars! :)
Un peu de publicité
Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir du contenu plus intéressant? Soutenez-nous en passant une commande ou en recommandant à des amis, Cloud VPS pour les développeurs à partir de 4,99 $ , un analogue unique des serveurs d'entrée de gamme que nous avons inventé pour vous: The Whole Truth About VPS (KVM) E5-2697 v3 (6 Cores) 10 Go DDR4 480 Go SSD 1Gbps à partir de 19 $ ou comment diviser correctement le serveur? (options disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).
Le Dell R730xd 2x est-il moins cher dans le centre de données Equinix Tier IV à Amsterdam? Seulement, nous avons 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2,6 GHz 14C 64 Go DDR4 4x960 Go SSD 1 Gbps 100 TV à partir de 199 $ aux Pays-Bas!Dell R420 - 2 x E5-2430 2,2 GHz 6C 128 Go DDR3 2 x 960 Go SSD 1 Gbps 100 To - À partir de 99 $! Lisez à propos de Comment construire l'infrastructure de bldg. classe avec les serveurs Dell R730xd E5-2650 v4 au coût de 9000 euros pour un sou?
