
Supprimer les nœuds d'un arbre rouge-noir n'est pas une tâche facile, il est donc logique de le diviser en plusieurs parties et de considérer chaque cas séparément.
cartoonbank.ru
Dans le dernier article, nous avons examiné les règles de formation d'un arbre de recherche rouge-noir et pris en compte les cas d'équilibrage lors de l'ajout d'éléments.
Parlons maintenant de la suppression d'éléments.
Prenons par exemple cet arbre rouge-noir:
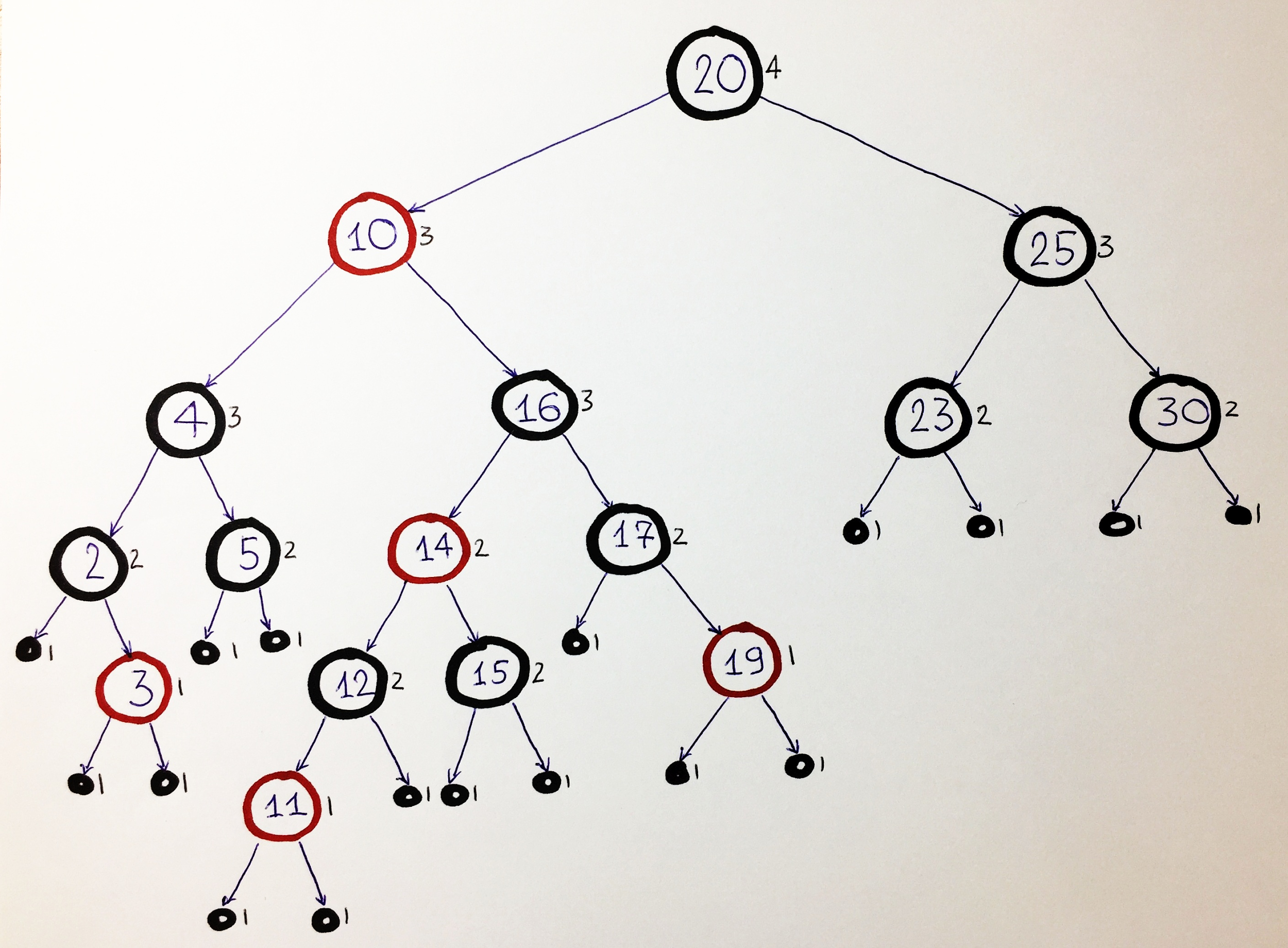
Rappelez-vous que la propriété principale d'un arbre rouge-noir est la même hauteur noire à gauche et à droite de chaque nœud. Par conséquent, sur les figures, à côté de chaque nœud, nous indiquerons la valeur de la hauteur du noir, afin qu'à chaque étape, nous puissions vérifier sa stabilité.
Diviser pour régner
Supprimer un élément d'un arbre rouge-noir n'est pas une tâche aussi facile que cela puisse paraître à première vue, je propose donc de le diviser en plusieurs parties et de considérer chacune séparément.
Commençons par diviser la tâche en deux catégories:
- couleur du nœud supprimé: K ou H
- nombre de nœuds enfants: 2, 1 ou 0
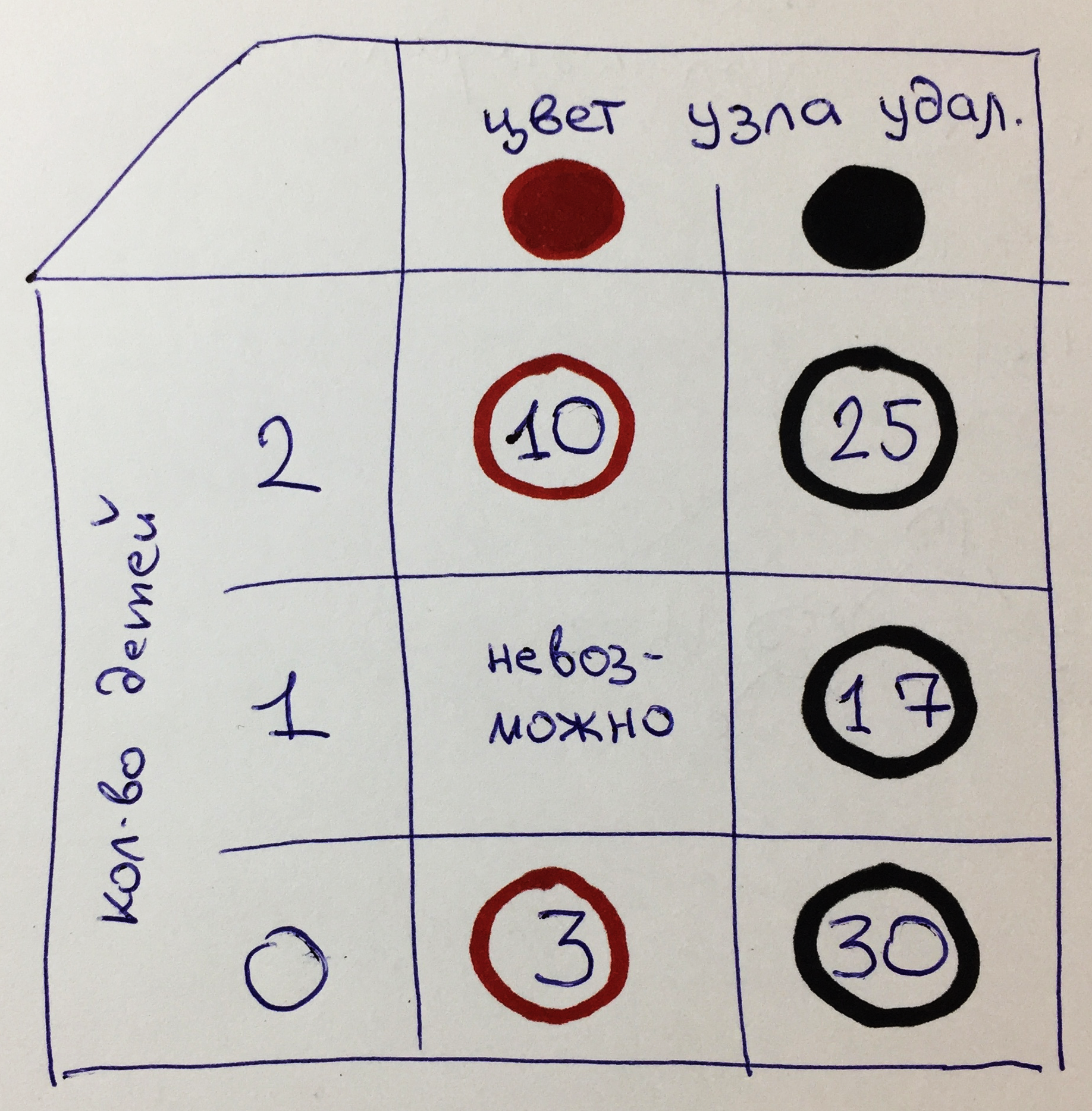
En conséquence, nous obtenons une matrice de 6 options: K2, Ch2, K1, Ch1, K0, Ch0.
Pour chaque option, le nœud correspondant de notre arbre est indiqué.
Considérons le processus de suppression pour chaque option.
K2 - noeud rouge avec deux enfants
La tâche de supprimer un nœud avec deux enfants est réduite à la tâche de supprimer un nœud avec un ou zéro enfant.
Pour ce faire, vous devez rechercher l'élément le plus proche qui est inférieur ou supérieur à l'élément supprimé et les échanger.

Veuillez noter que lors de l'échange d'éléments, il vous suffit de changer les valeurs dans les nœuds et de laisser la même couleur, afin de ne pas casser l'arborescence et de ne pas modifier la hauteur du noir.
Après l'échange, vous devez supprimer l'article de son nouvel emplacement. Ce sera soit l'élément le plus à droite dans la branche gauche (maximum à gauche), soit le plus à gauche à droite (minimum à droite), en aucun cas il n'aura un enfant à gauche ou à droite. Ainsi, la tâche de supprimer un nœud avec 2 enfants est réduite à la tâche de supprimer un élément avec 1 ou 0 enfants:
- K2 => K1 ou K0
Ch2 - noeud noir avec deux enfants
Comme dans le cas précédent, nous allons donner un exemple de suppression du nœud noir 16.

Comme vous pouvez le voir, après l'échange, la tâche se réduit à supprimer un élément avec un enfant:
- Ch2 => Ch1 ou Ch0
K1 - noeud rouge avec un enfant
Si le nœud rouge n'a pas un enfant, alors à la place il y a un élément NIL noir et la hauteur noire du nœud rouge est 1. Par conséquent, d'un autre côté, la hauteur noire devrait également être 1. Mais puisque le nœud rouge ne peut pas avoir d'enfant rouge couleurs, alors son autre enfant devrait être noir. Puisque la hauteur du noir doit être de 1, il ne peut s'agir que d'un élément noir NIL, car dans le cas d'un élément noir normal, la hauteur sera plus élevée.
Ainsi, le cas K1 n'a pas lieu.
Ch1 - noeud noir avec un enfant
Si l'élément noir n'a pas un enfant, alors il y a à la place un élément noir NIL avec une hauteur noire 1. Par conséquent, de l'autre côté, il devrait y avoir un nœud rouge sans enfants. Pour supprimer un tel élément, il suffit de transférer la valeur de l'élément rouge vers le nœud noir, tandis que la hauteur noire sera conservée.
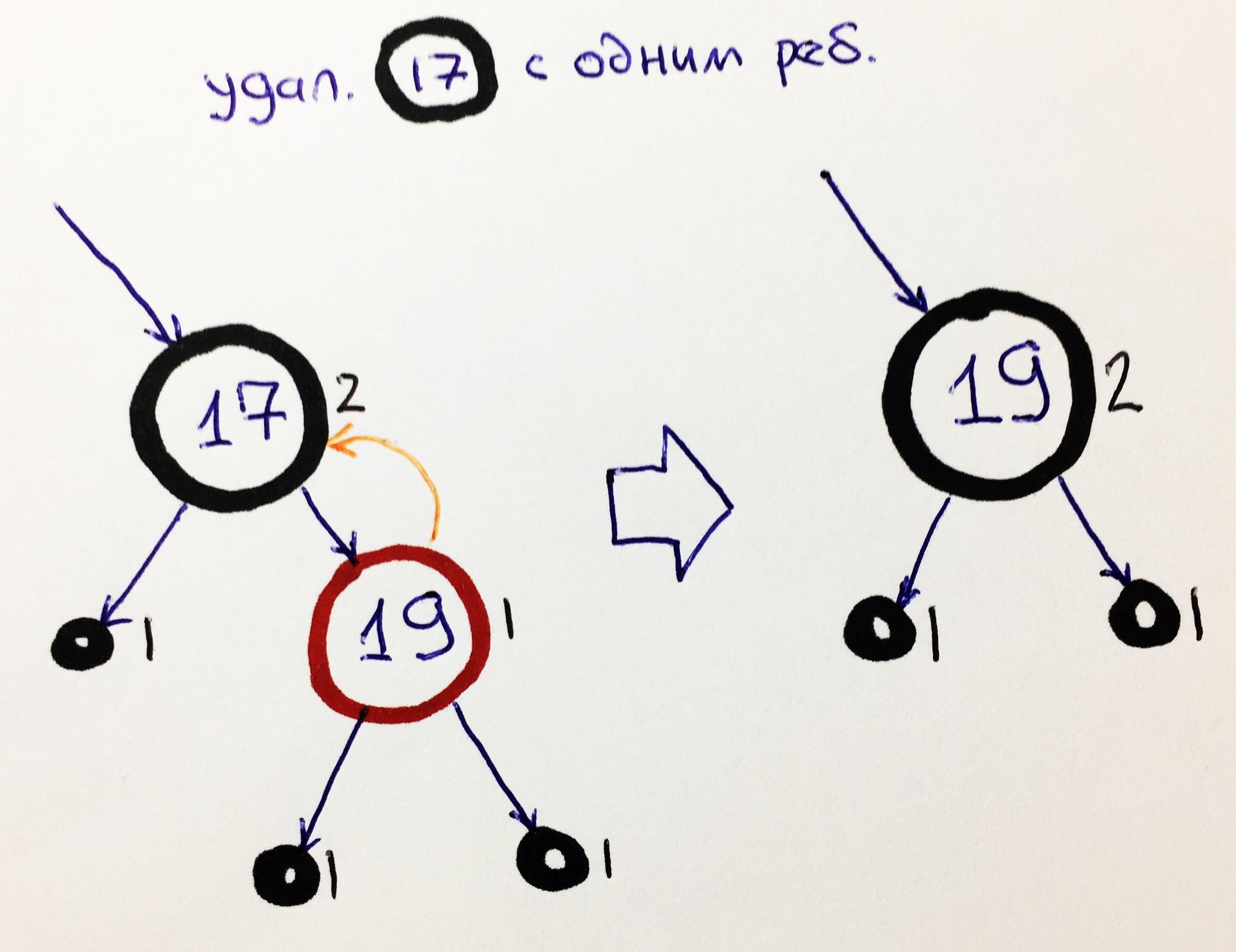
K0 - noeud rouge sans enfants
Le cas le plus simple. Nous supprimons simplement l'élément, en le remplaçant par une référence NIL: la
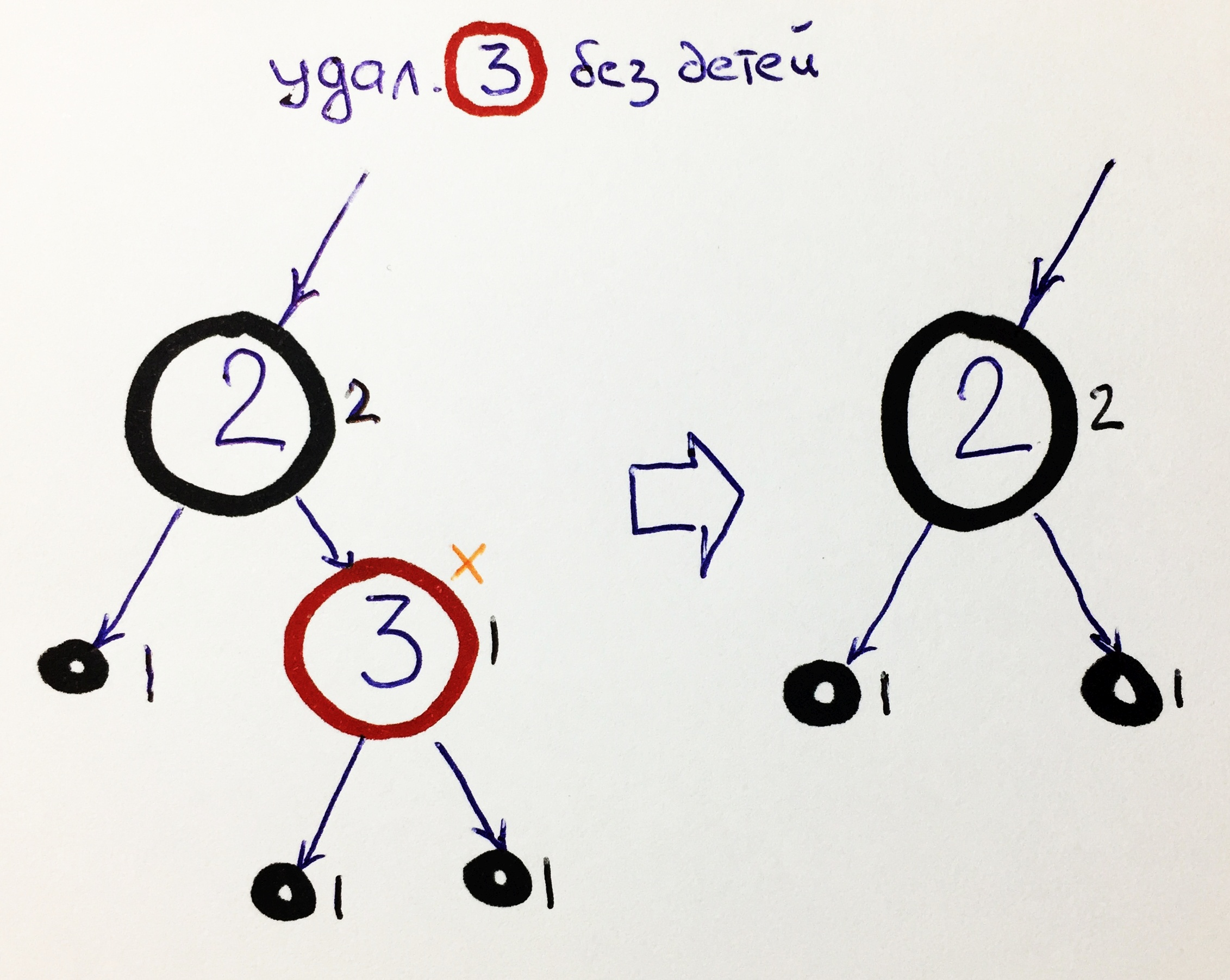
suppression de l'élément rouge ne change pas la hauteur du noir.
CH0 - noeud noir sans enfants
Supprimer un nœud noir sans enfants est également très simple: nous le remplaçons par une référence à NIL.
Pensez-vous que c'est presque tout? Haha, six fois.

Après avoir supprimé l'élément noir, la hauteur du noir du sous-arbre change et vous devez l'équilibrer pour son parent.
L'élément supprimé dans les figures est désigné par x, sa hauteur - h. Lorsque nous commençons juste à équilibrer, h = 1, mais avec les appels récursifs, cela peut augmenter.
Pour plus de précision, établissons que l'élément supprimé était le bon enfant. Après le retrait, sa hauteur a diminué et est devenue h. Cela signifie que la hauteur des fils de gauche reste h + 1. Nous devons aligner les hauteurs des sous-arbres gauche et droit et les rendre égales à h + 1.
Je suggère de diviser à nouveau la tâche en plusieurs parties. Quelles options avons-nous?
Le parent peut être rouge ou noir. Les fils de gauche peuvent également être noirs ou rouges. Et le bon fils est toujours noir - c'est à partir de là que nous sommes arrivés à l'équilibrage après le retrait.
Il y a 6 cas différents à considérer:
- KCH1 et KCH2 - le parent est rouge, l'enfant gauche est noir.
- CHK3 et CHK4 - le parent est noir, l'enfant gauche est rouge.
- HH5 et HH6 - le parent est noir, l'enfant de gauche est noir.
Nous ferons le plein de patience et de pop-corn, les mensonges les plus intéressants et mystérieux à venir.
1 - parent rouge, enfant gauche noir avec petits-enfants noirs
Tant que nous avons les nœuds rouges, nous pouvons les déplacer et / ou les recolorer pour rétablir l'équilibre de la hauteur du noir. Dans ce cas, nous pouvons abaisser la couleur rouge du parent aux fils de gauche, alignant ainsi la hauteur noire du parent:

Assurez-vous de vérifier à partir de la figure que les hauteurs noires des nœuds a et b sont conservées et que la hauteur de tout le sous-arbre est devenue la même et égale à h + 1.
2 - le parent est rouge, l'enfant gauche est noir avec le petit-fils rouge gauche.
Dans ce cas, repeindre à lui seul ne suffit pas. Nous devons faire un petit tour à droite entre les nœuds 3-7. En conséquence, nous pourrons augmenter la hauteur du sous-arbre droit à h + 1: un
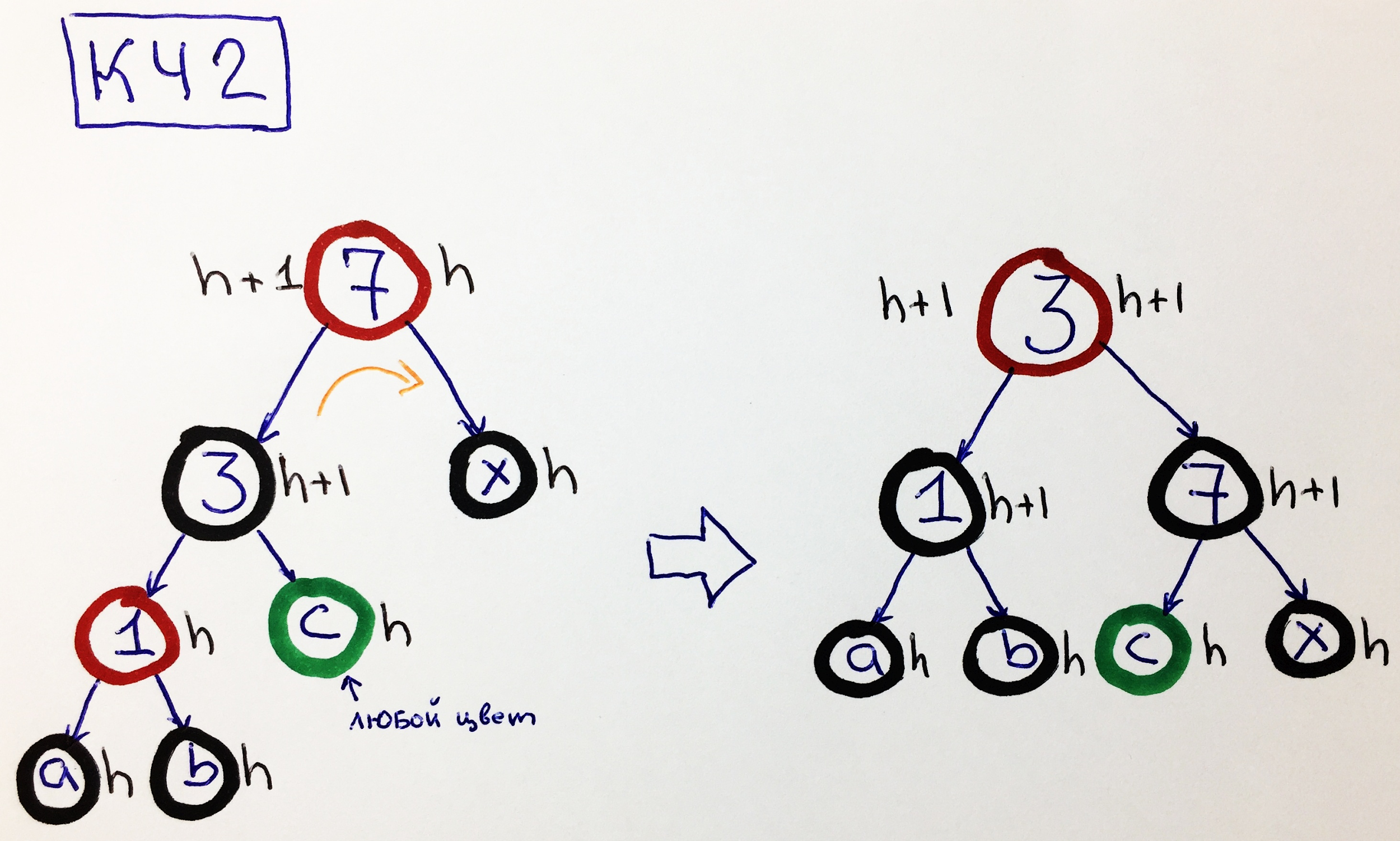
nœud vert signifie qu'il peut être noir ou rouge.
Remarque. Si le nœud «1» est noir et «c» est rouge, alors le problème peut être réduit à la variante HH5.
CHK3 - le parent est noir, le fils gauche est rouge, le petit-fils droit a des arrière-petits-enfants noirs
Avoir des arrière-petits-enfants noirs vous permet de repeindre le petit-fils en rouge et de l'envoyer au bon sous-arbre en faisant un petit virage à droite 3-7, et ne demandez pas pourquoi, faites simplement confiance et vérifiez que la hauteur du noir s'est stabilisée:
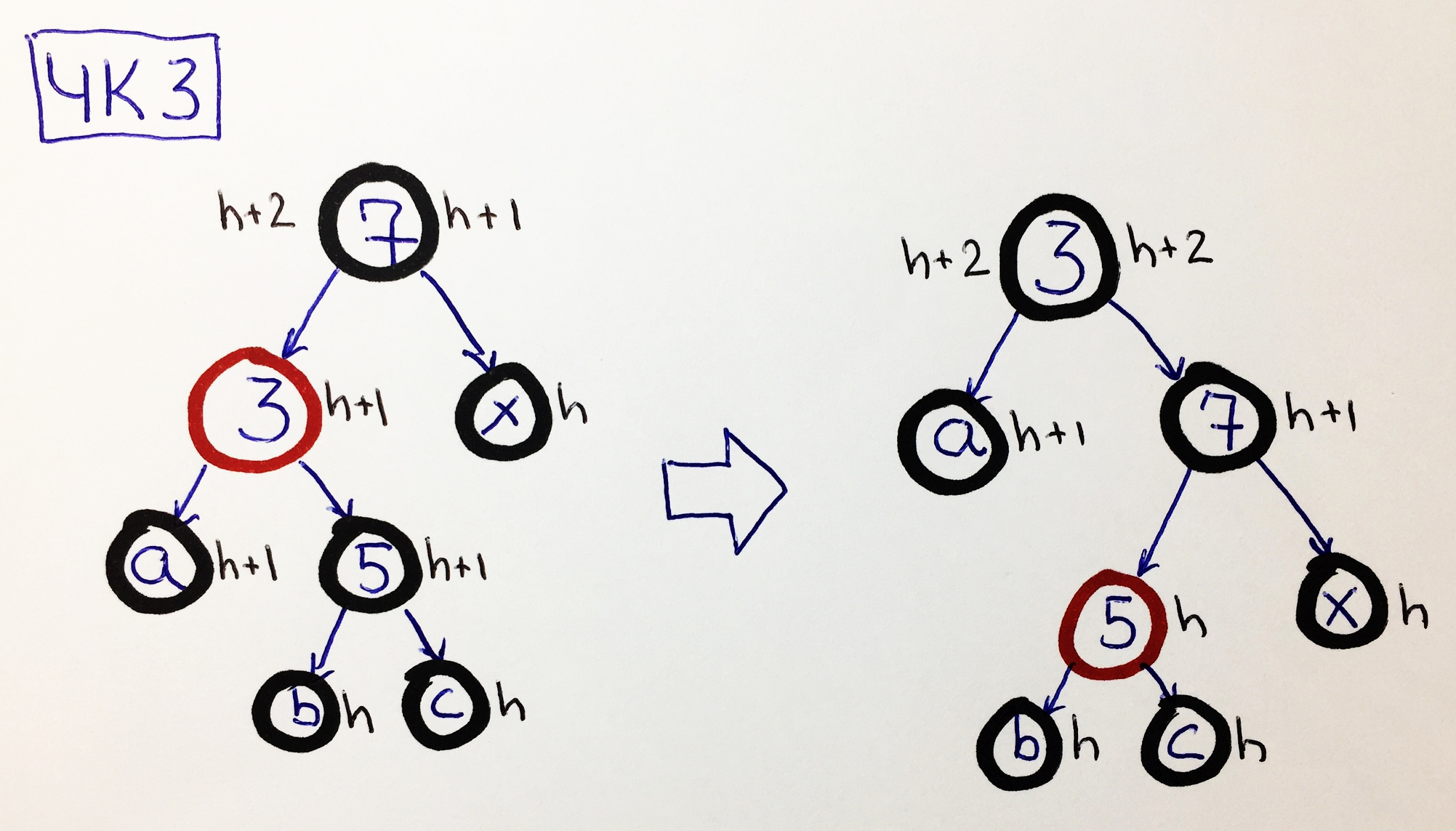
Notez que le nœud rouge 5 n'augmente pas le noir la taille.
CHK4 - le parent est noir, le fils gauche est rouge, le petit-fils droit a un arrière-petit-fils rouge
Plus loin dans la forêt rouge, il y a plus de bois de chauffage noirs, et il y en a de moins en moins de rouges, à savoir qu'en recolorant les nœuds rouges, il est possible de stabiliser la hauteur noire.

Dans ce cas, vous devez effectuer un grand virage à gauche, qui consiste en deux petits virages 5-3 et 5-7. Le nœud b a changé sa couleur du rouge au noir et a donc augmenté sa hauteur de 1. Assurez-vous que la hauteur du noir s'est stabilisée.
HCH5 - le parent est noir, le fils gauche est noir avec le petit-fils rouge droit.
De moins en moins d'éléments rouges dans notre sous-arbre, repeignez le dernier petit-fils rouge en noir et faites un grand virage à gauche, comme dans le cas précédent.

Vérifiez que la hauteur du noir du sous-arbre s'est stabilisée.
HCH6 - le parent est noir, le fils de gauche est noir, ses petits-enfants sont également noirs
Et puis est venu le moment où le bois rouge s'est épuisé. Il n'y a rien à faire, il faut peindre le nœud noir en rouge et ainsi égaliser la hauteur noire du nœud 7, mais pas en augmentant la hauteur noire du sous-arbre droit, mais en diminuant la hauteur noire du sous-arbre gauche. En conséquence, la hauteur noire de toute notre structure diminuera de 1 et nous devons appeler récursivement l'équilibre aux ancêtres.

Exemple de suppression avec équilibrage et récursivité
Nous avons couvert les 6 cas d'équilibrage de la hauteur noire après avoir retiré un élément de l'arbre rouge-noir. Pour avoir une meilleure idée de la façon dont tout cela fonctionne, continuons à supprimer le nœud 30 de l'arborescence d'origine.
La première étape consiste simplement à supprimer le nœud 30. La
deuxième étape consiste à lancer l'équilibrage sur son parent - le nœud 25.
Il y a un cas de HH6:

la hauteur du nœud 25 a été stabilisée avec un chagrin de moitié.
La troisième étape consiste à équilibrer au niveau du grand-père - pour le nœud 20.
Pour le rendre plus amusant et plus clair , dessinons l'arbre entier avant et après l'équilibrage. C'est le cas pour HK4:

remarquez comment l'arbre rouge-noir a changé après l'équilibrage, certains éléments du sous-arbre de gauche déplacés vers la droite, la hauteur s'est stabilisée, l'élément a été supprimé, tout le monde est content!
La suppression d'éléments d'un arbre rouge-noir est l'une des opérations les plus difficiles lorsque vous travaillez avec des arbres de recherche binaires. Dans le cours " Algorithmes et structures de données ", nous considérons non seulement les arbres de recherche binaires, mais aussi de nombreux autres algorithmes intéressants, pour plus de détails, voir le programme du cours.
