La renormalisation est sans doute la percée la plus importante en physique théorique au cours des 50 dernières années.

Vous n'avez pas besoin d'analyser le comportement des molécules d'eau individuelles pour comprendre le comportement des gouttes ou d'analyser les gouttes pour comprendre les vagues. La capacité de changer de focus entre différentes échelles est l'essence même de la renormalisation
Dans les années 1940, les physiciens pionniers sont tombés sur une nouvelle couche de réalité. Les particules ont été remplacées par des champs - des entités englobantes et agitées qui remplissaient tout l'espace à la manière d'un océan. Une petite ondulation dans un tel champ pourrait représenter un électron, l'autre un photon, et leurs interactions, apparemment, pourraient expliquer tous les phénomènes électromagnétiques.
Il n'y avait qu'un seul problème - toute cette théorie était basée sur des espoirs et des prières. Seulement avec l'aide d'une technique telle que la « renormalisation"En dissimulant soigneusement des quantités infinies, les chercheurs ont pu contourner les prédictions absurdes de la théorie. Le circuit a fonctionné, mais même ceux qui ont développé la théorie soupçonnaient qu'il pourrait s'agir d'un château de cartes s'accrochant à une astuce mathématique tordue.
«J'appellerais cela un 'processus fou'», a écrit plus tard Richard Feynman. «Nous avons dû nous en tenir à de telles astuces, c'est pourquoi nous n'avons pas été en mesure de prouver que la théorie de l'électrodynamique quantique est mathématiquement cohérente.
La théorie a été justifiée plus tard, après plusieurs décennies, et grâce au domaine apparemment sans rapport de la physique. Les chercheurs qui ont étudié la magnétisation ont découvert que la renormalisation ne concerne pas du tout l'infini. Cette théorie concerne la division de l'univers en royaumes de tailles indépendantes. Et cette perspective régit aujourd'hui de nombreux aspects de la physique.
David Tong , physicien théoricien à l'Université de Cambridge, écrit que la renormalisation est «peut-être la percée la plus importante en physique théorique des 50 dernières années».
Une histoire de deux charges
D'un certain point de vue, les théories des champs sont les théories les plus réussies en science. La théorie de l'électrodynamique quantique (QED), l'un des piliers du modèle standard de la physique des particules, a produit des prédictions théoriques qui coïncident avec des expériences allant jusqu'à des milliardièmes.
Mais dans les années 30 et 40, l'avenir de la théorie n'était pas si certain. Approcher le comportement complexe des champs a souvent produit des réponses sans signification et infinies, ce qui a amené certains théoriciens à croire que les théories des champs sont une impasse.
Feynman et d'autres ont commencé à chercher de nouvelles perspectives - peut-être celles qui ramèneraient des particules sur la scène - mais ont plutôt trouvé une astuce. Ils ont constaté que les équations QED donnent des prédictions raisonnables lorsqu'elles leur sont appliquées par une procédure de renormalisation cryptique.
L'exercice ressemble à quelque chose comme ça. Si les calculs QED donnent un montant infini, coupez-le. Convertissez la partie qui veut aller à l'infini en un coefficient fixe devant la somme. Remplacez-le par la mesure finale prise en laboratoire. Enfin, laissez le montant corrigé courir à l'infini.
Pour certains physiciens, cette recette était comme jouer dans une coquille. «On ne peut tout simplement pas appeler cela des mathématiques significatives», a écrit l' éminent théoricien quantique Paul Dirac .
Le nœud du problème - et le premier pas vers une solution ultérieure - est la façon dont les physiciens travaillent avec la charge d'un électron.
Dans le schéma décrit, la charge électrique provient d'un coefficient - une valeur qui avale l'infini dans le processus de brassage mathématique. Pour les théoriciens, perdus dans les conjectures sur la signification physique de la renormalisation, QED a laissé entendre que l'électron a deux charges: théorique, infinie et mesurable, finie. Peut-être que la charge dans le noyau d'un électron est infinie. Mais en pratique, l'effet d'un champ quantique (qui peut être imaginé comme un nuage virtuel de particules chargées positivement) enveloppe l'électron de sorte que les expérimentateurs ne mesurent qu'une charge nette modeste.
Deux physiciens, Murray Gell-Manet Francis Lowe, a formalisé cette idée en 1954. Il a couplé deux charges d'un électron avec une charge «effective», variant avec la distance. Plus vous vous rapprochez (plus vous vous enfoncez dans le nuage d'électrons positifs), plus vous voyez de charge.
Leurs travaux ont d'abord lié la renormalisation à l'idée d'échelle. On peut en conclure que les physiciens quantiques ont trouvé la bonne réponse à la mauvaise question. Au lieu de se soucier de l'infini, ils ont dû faire face à la fusion du minuscule avec l'énorme.
La renormalisation est "une version mathématique du microscope", a déclaré Astrid Eichhorn, physicien à l'Université du Danemark du Sud utilisant la renormalisation pour rechercher des théories de la gravité quantique. «Inversement, vous pouvez commencer avec le système microscopique et effectuer un zoom arrière. C'est une combinaison d'un microscope et d'un télescope. "
Les aimants sauvent la journée
Le deuxième indice provient du monde de la matière condensée , où les physiciens se sont demandé comment un modèle grossier d'aimant pouvait prédire avec précision les détails subtils de certaines transformations. Le modèle d'Ising n'était qu'une grille de flèches atomiques, dont chacune ne pouvait pointer que vers le haut ou vers le bas - et pourtant, il prédisait le comportement de vrais aimants avec une précision incroyable.
À basse température, la plupart des atomes s'alignent, ce qui magnétise la substance. À des températures élevées, un désordre se produit et le réseau est démagnétisé. Mais au point de transition critique, il y a des îlots d'atomes alignés de différentes tailles. Ce qui est important, la distribution de certaines quantités à ce point critique s'avère être la même dans le modèle d'Ising, dans de vrais aimants de matériaux différents, dans des systèmes non connectés à des aimants, comme une transition à haute pression, lorsque l'eau devient indiscernable de la vapeur. La découverte de ce soi-disant. la polyvalence était aussi étrange que la découverte que la vitesse maximale des éléphants et des aigrettes était exactement la même.
Les physiciens ne travaillent généralement pas avec des objets de différentes tailles en même temps. Cependant, ce comportement universel au voisinage du point critique les a obligés à traiter des longueurs de toutes les échelles à la fois.
Leo Kadanov, un chercheur en matière condensée, a compris comment y faire face en 1966. Il a développé la technique du "fractionnement des spins en blocs". Le réseau d'Ising, trop complexe pour travailler directement, a été divisé en blocs de taille modeste, avec plusieurs flèches de chaque côté. Il a calculé l'orientation moyenne du groupe de flèches et a remplacé le bloc entier par cette valeur. En répétant le processus, il a lissé les détails du maillage fin en effectuant un zoom arrière afin de comprendre le comportement général du système.
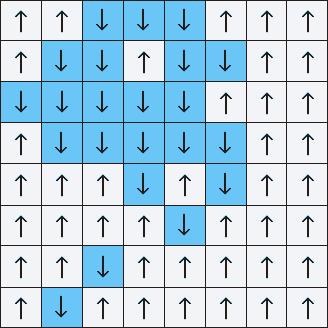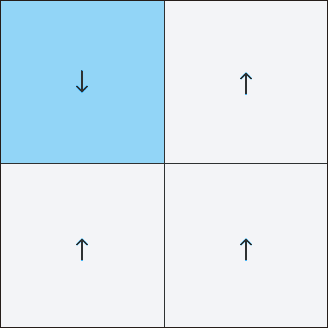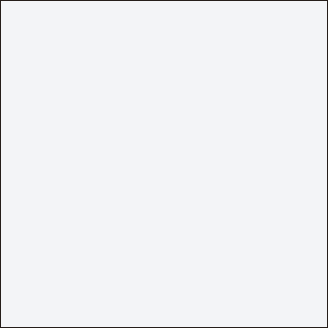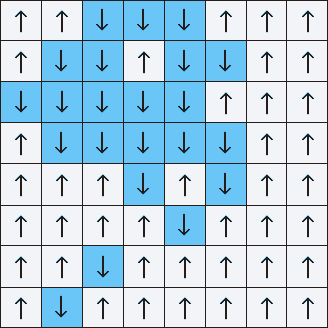
La renormalisation de spin de bloc fait la moyenne d'une grille avec de nombreux spins individuels, les transformant en blocs de taille toujours croissante
Enfin, Ken Wilson - un ancien élève de Gell-Man, qui s'est immédiatement engagé dans la physique des particules et la physique de la matière condensée - a combiné les idées de Gell-Man et Lowe avec celles de Kadanoff. Son « groupe de renormalisation », décrit par lui pour la première fois en 1971, justifiait les calculs de QED pervertis et fournissait une échelle pour les systèmes universels. Ce travail lui a valu un prix Nobel et a changé la physique pour toujours.
Paul Fendley , un scientifique de la matière condensée à l'Université d'Oxford, estime qu'il est préférable de présenter le concept du groupe de renormalisation de Wilson comme une «théorie des théories» combinant le microscopique et le macroscopique.
Prenons une grille magnétique. Au niveau microscopique, il est facile d'écrire une équation reliant deux flèches adjacentes. Cependant, il sera presque impossible d'extrapoler cette formule à des milliards de particules. Vous êtes sur la mauvaise échelle.
Le groupe de renormalisation de Wilson décrit la transformation de la théorie des blocs de construction en théorie des structures. Vous commencez par la théorie des petits morceaux, disons, les atomes d'une boule de billard. Tournez la poignée de l'appareil mathématique de Wilson et vous avez une théorie connexe décrivant des groupes de ces pièces - par exemple, les molécules d'une boule de billard. Tournez plus loin, l'échelle diminue et les volumes des groupes augmentent - des amas de molécules, des secteurs d'une boule de billard, etc. apparaissent. En conséquence, il sera possible de calculer quelque chose d'intéressant - par exemple, le chemin de la balle entière.
C'est la magie du groupe de renormalisation: il permet de déterminer quelles quantités seront utiles à mesurer et quels détails microscopiques complexes peuvent être ignorés. Le surfeur s'intéresse à la hauteur des vagues, pas à l'écrasement des molécules d'eau. En physique subatomique, la renormalisation indique aux physiciens quand ils peuvent travailler avec un proton relativement simple au lieu de l'enchevêtrement de ses quarks internes.
Le groupe de renormalisation de Wilson a également suggéré que les malheurs de Feynman et de ses contemporains provenaient de tentatives pour comprendre l'électron tout en étant infiniment proche de lui. «On ne peut pas s'attendre à ce que les théories fonctionnent à n'importe quelle échelle de distance, même petite», a déclaré James Fraser., philosophe de la physique de l'Université de Durham en Grande-Bretagne. Les physiciens comprennent maintenant que couper les sommes et mélanger les infinis est la bonne façon de faire le calcul lorsque votre théorie a une taille de grille minimale. «La suppression de l'excédent compense notre ignorance de ce qui se passe aux niveaux inférieurs», a déclaré Fraser.
En d'autres termes, QED et le modèle standard sont tout simplement incapables de dire quelle sera la charge électronique à une distance de zéro nanomètre. De telles théories de la physique sont dites «efficaces». Ils fonctionnent mieux à des distances bien définies. L'objectif principal de la physique des hautes énergies est de comprendre ce qui se passe lorsque les particules se rapprochent.
Du grand au petit
Aujourd'hui, le «processus fou» de Feynman est utilisé en physique aussi souvent que l'algèbre, et son application est à la fois responsable des plus grandes avancées dans ce domaine et des défis actuels. Lors de la renormalisation, les subtilités submicroscopiques complexes disparaissent généralement. Peut-être existent-ils, mais ils n'affectent pas le tableau d'ensemble. «La simplicité est une bénédiction», a déclaré Fendley. "Il y a quelque chose de divin là-dedans."
Ce fait mathématique décrit la tendance de la nature à se diviser en mondes largement indépendants. Lors de la conception d'un gratte-ciel, les ingénieurs ignorent les molécules d'acier individuelles. Les chimistes analysent les liaisons moléculaires tout en ignorant parfaitement les quarks et les gluons. La division des phénomènes par dimensions linéaires, exprimée numériquement en groupes de renormalisation, a permis aux scientifiques au fil des siècles de passer progressivement du grand au petit, au lieu d'attaquer toutes les dimensions simultanément.
Pourtant, en même temps, l'hostilité de la renormalisation envers les détails microscopiques travaille contre les physiciens modernes désireux de découvrir des signes de la prochaine échelle du micromonde. Du principe de la séparation des échelles, il s'ensuit qu'ils devront creuser plus profondément pour surmonter la tendance de la nature à cacher de petits détails à des géants curieux comme nous.
«La renormalisation nous aide à simplifier la tâche», a déclaré Nathan Seiberg , physicien théoricien à l'Institute for Advanced Study de Princeton. «Cependant, elle cache également ce qui se passe à courte distance. Vous ne pouvez pas tout obtenir tout de suite. "