Dans une bonne ville près de Moscou, il y a un mauvais passage à niveau. Aux heures de pointe, non seulement il monte, mais aussi les intersections et les routes voisines. Au volant encore une fois, je me suis demandé - quelle est sa capacité et quelque chose peut-il être changé?

Pour répondre à cette question, nous allons nous plonger un peu dans la réglementation et la théorie des flux de trafic, analyser les données GPS et accéléromètre à l'aide de Python et comparer les calculs théoriques avec les données expérimentales.
Contenu
1.
, 10 /. .
Jupyter Notebook GitHub'.

:
import pandas as pd
import numpy as np
import glob
#!pip install utm
import utm
from sklearn.decomposition import PCA
from scipy import interpolate
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(rc={'figure.figsize':(12, 8)})
import plotly.express as px
# Mapbox Plotly
mapbox_token = open('mapbox_token', 'r').read()2.
.
— 1 .
:
« » . , 2005 . , .

218.2.020-2012 " ".
, :
, :
, , .
2 :
- ;
- .
:
- :
- :
#
diagram1 = pd.read_csv(' .csv', sep=';', header=None, names=['P', 'V'], decimal=',')
diagram1_func = interpolate.interp1d(diagram1['P'], diagram1['V'], kind='cubic')
diagram1_xnew = np.arange(diagram1['P'].min(), diagram1['P'].max())
#
diagram2 = pd.read_csv(' .csv', sep=';', header=None, names=['P', 'Q'], decimal=',')
diagram2_func = interpolate.interp1d(diagram2['P'], diagram2['Q'], kind='cubic')
diagram2_xnew = np.arange(diagram2['P'].min(), diagram2['P'].max())def density_Tanaka(V):
#
V = V * 1000 / 60 / 60 # / /
L = 5.7 #
c1 = 0.504 #
c2 = 0.0285 #**2/
return 1000 / (L + c1 * V + c2 * V**2) # ./
def density_Grindshilds(V):
#
pmax = 85 # ./
vmax = 60 # /
return pmax * (1 - V / vmax) # ./#
V = np.arange(1, 80) # /
V1 = np.arange(1, 61) # /
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))
ax1.plot(density_Tanaka(V), V, label=" ")
ax1.plot(density_Grindshilds(V1), V1, label=" ")
ax1.plot(diagram1_xnew, diagram1_func(diagram1_xnew), label=". ")
ax1.set_xlabel(r' $\rho$, /')
ax1.set_ylabel(r' $V$, /')
ax1.legend()
ax2.plot(density_Tanaka(V), density_Tanaka(V) * V, label=" ")
ax2.plot(density_Grindshilds(V1), density_Grindshilds(V1) * V1, label=" ")
ax2.plot(diagram2_xnew, diagram2_func(diagram2_xnew), label=". ")
ax2.set_xlabel(r' $\rho$, /')
ax2.set_ylabel(r' $Q$, /')
ax2.legend()
plt.show()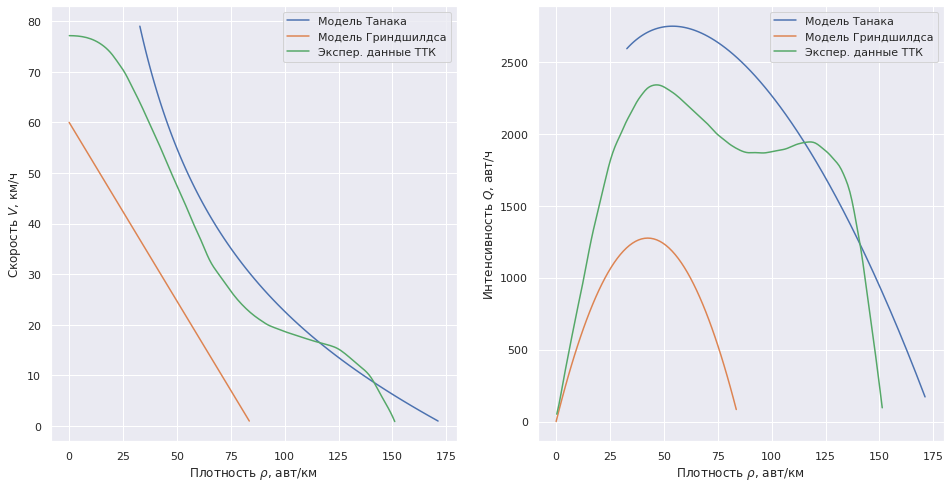
. .
3.
3.1
, . Enter, :
%%writefile "key-logger.py"
import pandas as pd
import time
import datetime
class _GetchUnix:
# from https://code.activestate.com/recipes/134892/
def __init__(self):
import tty, sys
def __call__(self):
import sys, tty, termios
fd = sys.stdin.fileno()
old_settings = termios.tcgetattr(fd)
try:
tty.setraw(sys.stdin.fileno())
ch = sys.stdin.read(1)
finally:
termios.tcsetattr(fd, termios.TCSADRAIN, old_settings)
return ch
def logging():
path = 'logs/keylog/'
filename = f"{time.strftime('%Y-%m-%d %H-%M-%S')}.csv"
path_to_file = path + filename
db = []
getch = _GetchUnix()
print('...')
while True:
key = getch()
if key == 'c':
break
else:
db.append((datetime.datetime.now(), key))
df = pd.DataFrame(db, columns=['time', 'click'])
print(df)
df.to_csv(path_to_file, index=False)
print(f"\nSaved to {filename}")
if __name__ == "__main__":
logging()20 . 2 , . . 100%:
files = glob.glob('logs/keylog/*.csv')
keylogger_data = []
print(f' - {len(files)} .')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'])
keylogger_data.append(df)
keylogger_data = pd.concat(keylogger_data, ignore_index=True)
keylogger_data.head()| time | click | |
|---|---|---|
| 0 | 2020-09-29 16:24:02.691189 | d |
| 1 | 2020-09-29 16:24:05.186670 | a |
| 2 | 2020-09-29 16:24:07.157702 | d |
| 3 | 2020-09-29 16:24:11.506961 | a |
| 4 | 2020-09-29 16:24:14.206266 | a |
"a" — , 'd' — .
:
keylogger_data['time'] = keylogger_data['time'].astype('datetime64[m]')
keylogger_per_min = keylogger_data.groupby(['click', 'time'], as_index=False).size().reset_index().rename(columns={0:'size'})
keylogger_per_min.head()| index | click | time | size | |
|---|---|---|---|---|
| 0 | 0 | a | 2020-09-29 16:24:00 | 12 |
| 1 | 1 | a | 2020-09-29 16:25:00 | 13 |
| 2 | 2 | a | 2020-09-29 16:26:00 | 9 |
| 3 | 3 | a | 2020-09-29 16:27:00 | 18 |
| 4 | 4 | a | 2020-09-29 16:28:00 | 14 |
sns.catplot(x='click', y='size', kind="box", data=keylogger_per_min);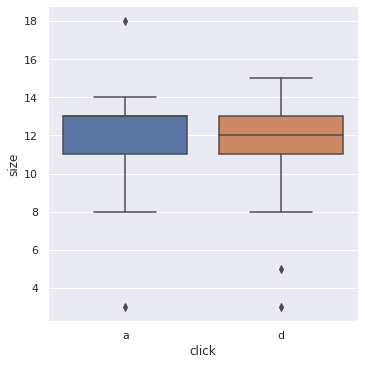
print(f" : {keylogger_per_min['size'].mean():.1f} ./ \
{keylogger_per_min['size'].mean() * 60:.1f} ./") : 11.7 ./ 700.0 ./
.
— 700 ./ 10 / ( 50 / ) — .
plt.plot(V1, density_Grindshilds(V1)*V1, label=" ")
plt.xlabel(r' $V$, /')
plt.ylabel(r' $Q$, /')
plt.show()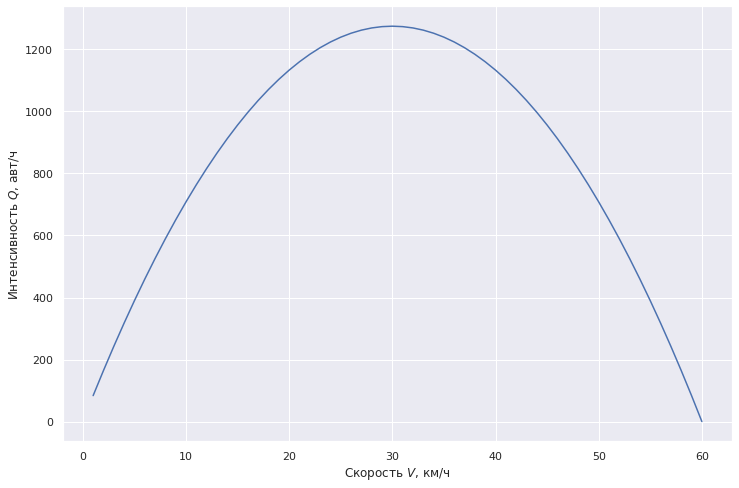
3.2
Android GPSLogger csv . ( ) GPS — Physics Toolbox Suite.
50 . — .
, — .
GPSLogger
GPSLogger , :
- time — ;
- lat lon — , ;
- speed — ,
m / de 2 - direction — , .
files = glob.glob('logs/gps/*.csv')
gpslogger_data = []
print(f' GPS - {len(files)} .')
for filename in files:
df = pd.read_csv(filename, parse_dates=['time'], index_col='time')
if df.iloc[10, 1] < df.iloc[-1, 1]:
df['direction'] = 0 #
else:
df['direction'] = 1 #
gpslogger_data.append(df)
gpslogger_data = pd.concat(gpslogger_data)
gpslogger_data.head()
gps_1 = gpslogger_data[['lat', 'lon', 'speed', 'direction']]GPS — 37 .
Physics Toolbox Suite:
files = glob.glob('logs/gps_accel/*.csv')
print(f' - {len(files)} .')
pts_data = []
for filename in files:
df = pd.read_csv(filename, sep=';',decimal=',')
df['time'] = filename[-22:-12] + '-' + df['time']
if df.iloc[10, 5] < df.iloc[-1, 5]:
df['direction'] = 0 #
else:
df['direction'] = 1 #
pts_data.append(df)
pts_data = pd.concat(pts_data)
pts_data.head()— 14 .
| time | ax | ay | az | Latitude | Longitude | Speed (m/s) | Unnamed: 7 | direction | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2020-09-04-14:11:18:029 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.00000 | 0.0 | NaN | 1 |
| 1 | 2020-09-04-14:11:18:030 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 2 | 2020-09-04-14:11:18:030 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 3 | 2020-09-04-14:11:18:094 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
| 4 | 2020-09-04-14:11:18:094 | 0.0 | 0.0 | 0.0 | 56.372343 | 37.53044 | 0.0 | NaN | 1 |
, — :
pts_data = pts_data.query('Latitude != 0.')Physics Toolbox Suite 400 , GPS 1 , :
pts_data['time'] = pd.to_datetime(pts_data['time'], format='%Y-%m-%d-%H:%M:%S:%f')
pts_data = pts_data.rename(columns={'Latitude':'lat', 'Longitude':'lon', 'Speed (m/s)':'speed'}):
accel_data = pts_data[['time', 'lat', 'lon', 'ax', 'ay', 'az', 'direction']].copy()
accel_data = accel_data.set_index('time')
accel_data['direction'] = accel_data['direction'].map({1.: ' ', 0.: ' '})
accel_data.head()| lat | lon | ax | ay | az | direction | |
|---|---|---|---|---|---|---|
| time | ||||||
| 2020-09-04 14:11:18.030 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | |
| 2020-09-04 14:11:18.030 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | |
| 2020-09-04 14:11:18.094 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | |
| 2020-09-04 14:11:18.094 | 56.372343 | 37.53044 | 0.0 | 0.0 | 0.0 | |
| 2020-09-04 14:11:18.095 | 56.372343 | 37.53044 | 0.0 | 0.0 | -0.0 |
GPS:
gps_2 = pts_data[['time', 'lat', 'lon', 'speed', 'direction']].copy()
gps_2 = gps_2.set_index('time')
gps_2 = gps_2.resample('S').mean()
gps_2 = gps_2.dropna(how='all')
gps_2.head()| lat | lon | speed | direction | |
|---|---|---|---|---|
| time | ||||
| 2020-08-10 00:45:02 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:03 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:04 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:05 | 56.338342 | 37.522946 | 0.0 | 1.0 |
| 2020-08-10 00:45:06 | 56.338342 | 37.522946 | 0.0 | 1.0 |
GPS :
gps_data = gps_1.append(gps_2, ignore_index=True)
gps_data['direction'] = gps_data['direction'].map({1.: ' ', 0.: ' '})
gps_data.head()| lat | lon | speed | direction | |
|---|---|---|---|---|
| 0 | 56.167241 | 37.504026 | 19.82 | |
| 1 | 56.167051 | 37.503804 | 19.36 | |
| 2 | 56.166884 | 37.503667 | 19.62 | |
| 3 | 56.166718 | 37.503554 | 19.35 | |
| 4 | 56.166570 | 37.503427 | 19.12 |
3.2.1
Plotly:
fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()
3.2.2
:
- GPS, WGS 84 .
- .
Web Mercator, — , , .
, . — , — (UTM).
Web-Mercator
UTM
UTM Python https://github.com/Turbo87/utm, .
gps_data['xs'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
gps_data['ys'] = gps_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
gps_data['speed_kmh'] = gps_data.speed / 1000 * 60 * 6050 :
#
lat0 = 56.35205
lon0 = 37.51792
xc, yc, _, _ = utm.from_latlon(lat0, lon0)
r = 50
gps_data = gps_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')fig = px.scatter_mapbox(gps_data, lat="lat", lon="lon", color='direction', zoom=17, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()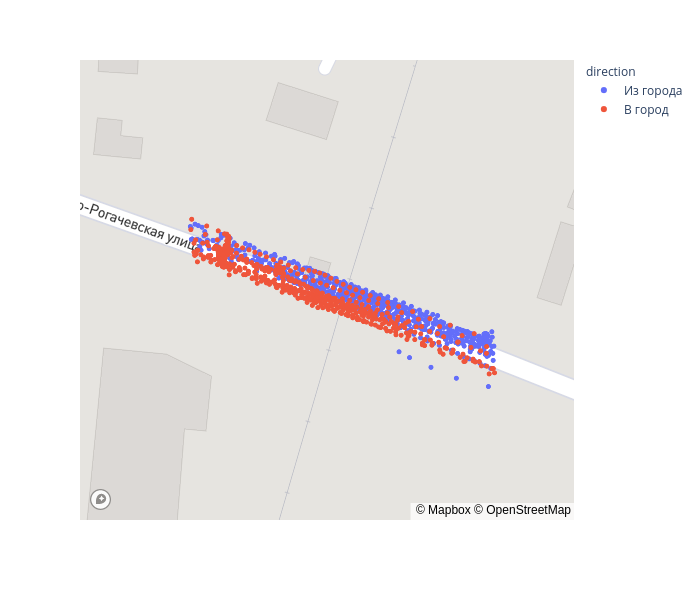
. 2d 1d, (PCA).
2 — scikit-learn. Sklearn:
pca = PCA(n_components=1).fit(gps_data[['xs', 'ys']])
gps_data['xs_transform'] = pca.transform(gps_data[['xs', 'ys']])sns.relplot(x='xs_transform', y='speed_kmh', data=gps_data, aspect=2.5, hue='direction');
. — [-5, 25]. .
accel_data['xs'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[0], axis=1)
accel_data['ys'] = accel_data[['lat', 'lon']].apply(lambda x: utm.from_latlon(x[0], x[1])[1], axis=1)
accel_data = accel_data.query(f'{xc - r} < xs & xs < {xc + r}')\
.query(f'{yc - r} < ys & ys < {yc + r}')
accel_data['xs_transform'] = pca.transform(accel_data[['xs', 'ys']]) Android :
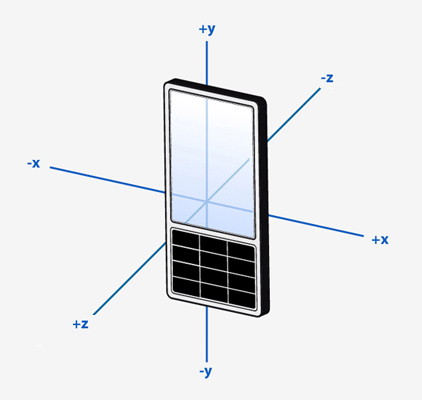
( Y). :
sns.relplot(x='xs_transform', y='ax', data=accel_data, aspect=2.5, hue='direction');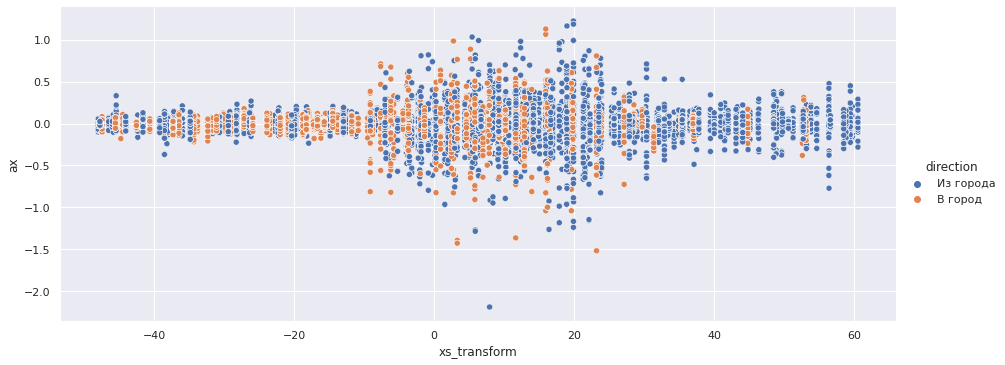
sns.relplot(x='xs_transform', y='ay', data=accel_data, aspect=2.5, hue='direction');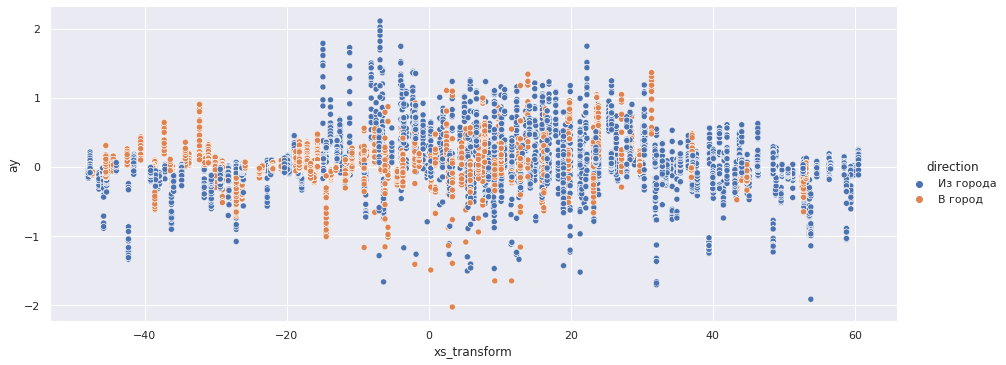
sns.relplot(x='xs_transform', y='az', data=accel_data, aspect=2.5, hue='direction');
Z:
sns.relplot(x='xs_transform', y='az', data=accel_data.query('-20 < xs_transform < 40'), aspect=2.5, hue='direction');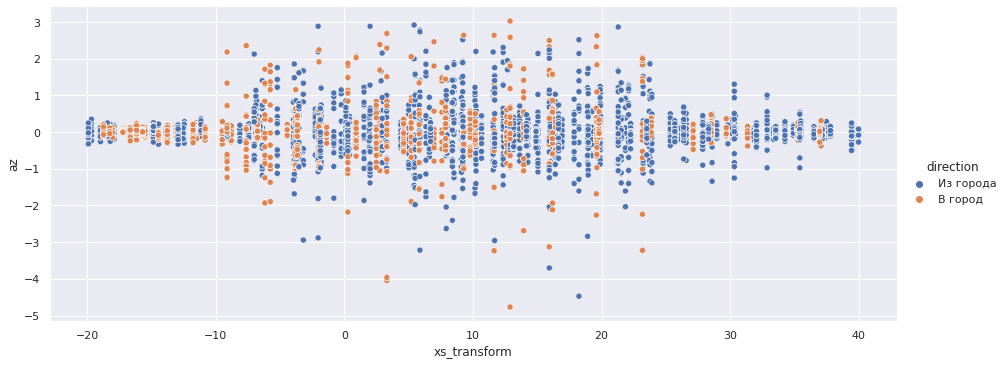
X Z — [-10, 25] 7.5.
cross = gps_data.query('-10 < xs_transform < 25')fig = px.scatter_mapbox(cross, lat="lat", lon="lon", color='direction', zoom=19, height=600)
fig.update_layout(mapbox_accesstoken=mapbox_token, mapbox_style='streets')
fig.show()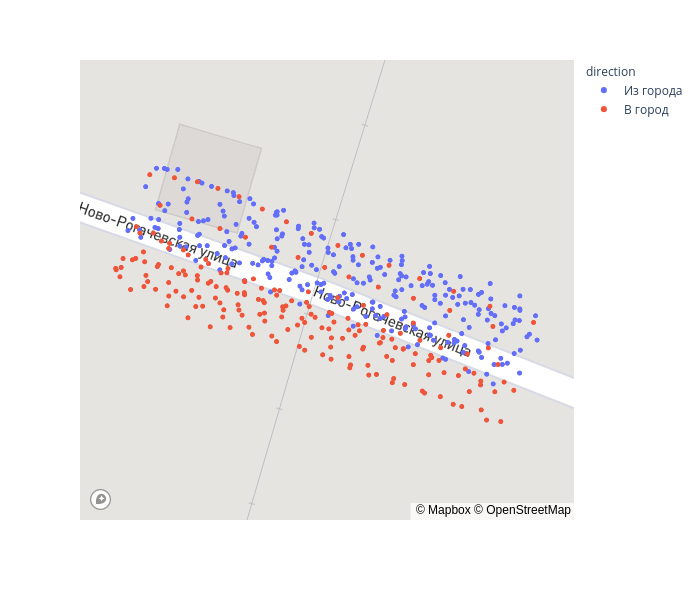
:
mean_v = cross.speed_kmh.mean()
print(f" - {mean_v:.2} /")
sns.distplot(cross.speed_kmh);— 9.4 /
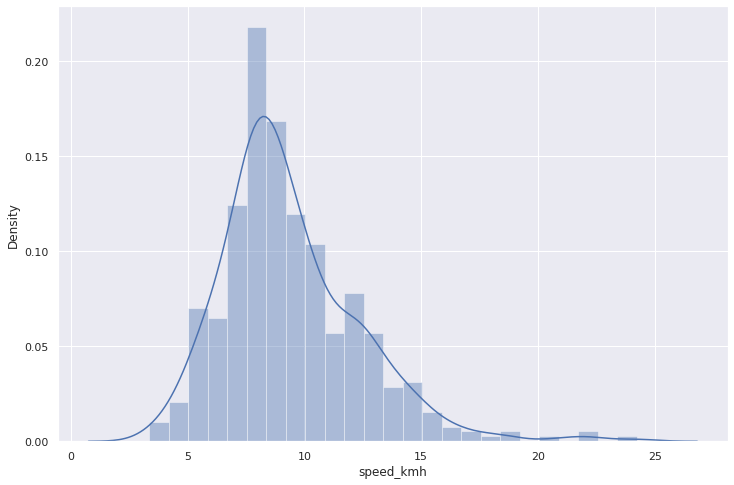
:
base = 1
gps_data['xs_transform_round'] = gps_data['xs_transform'].apply(lambda x: base * round(x / base))
accel_data['xs_transform_round'] = accel_data['xs_transform'].apply(lambda x: base * round(x / base))sns.relplot(x='xs_transform_round', y='speed_kmh', data=gps_data, kind="line", aspect=2.5);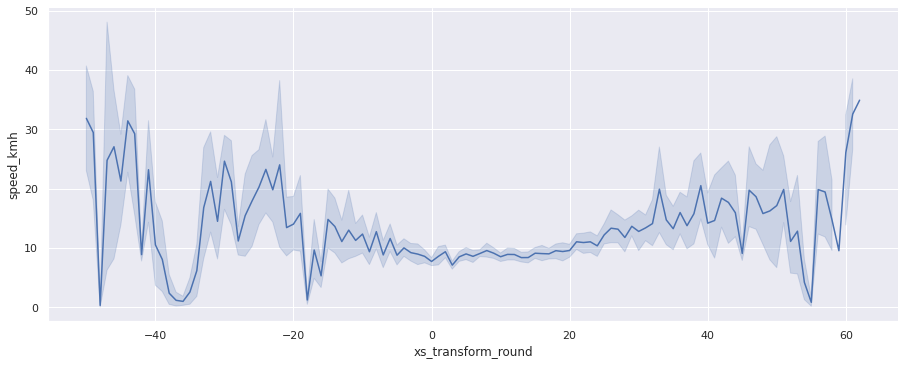
sns.relplot(x='xs_transform_round', y='az', data=accel_data, kind="line", aspect=2.5);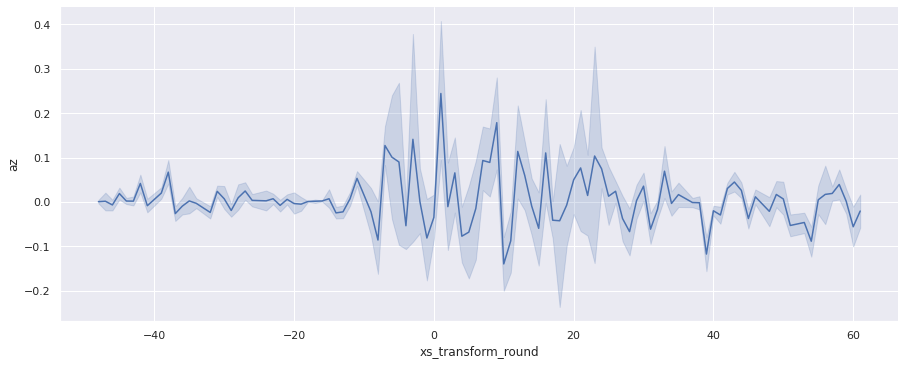
3.3
:
gps_data['flow_Tanaka'] = density_Tanaka(gps_data.speed_kmh) * gps_data.speed_kmh
gps_data['flow_Grindshilds'] = density_Grindshilds(gps_data.speed_kmh) * gps_data.speed_kmhsns.relplot(x='xs_transform_round', y='flow_Grindshilds', data=gps_data, aspect=2.5, kind='line', hue='direction');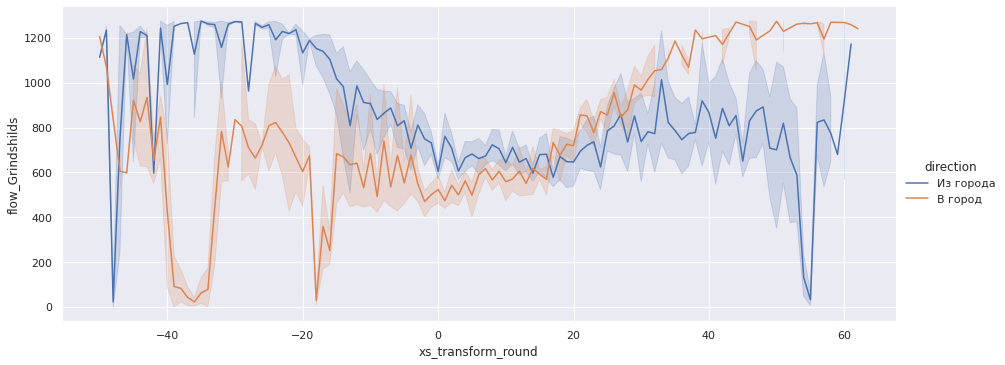
cross = gps_data.query('-10 < xs_transform < 25')mean_flow_Tanaka = cross.flow_Tanaka.mean()
print(f" - {mean_flow_Tanaka:.1f} / \
{mean_flow_Tanaka / 60:.1f} /")— 1275.5 / 21.3 /
mean_flow_Grindshilds = cross.flow_Grindshilds.mean()
print(f" - {mean_flow_Grindshilds:.1f} / \
{mean_flow_Grindshilds / 60:.1f} /") — 660.0 / 11.0 /
, 700 ./.
plt.plot(V1, density_Grindshilds(V1)*V1, label=" ")
plt.xlabel(r' $V$, /')
plt.ylabel(r' $Q$, /')
plt.show()
, - 30 / — .
, :
4.
Sur la base de notre analyse, on peut affirmer que le passage à niveau est dans un état insatisfaisant et que le débit est d'environ 10 km / h, ce qui, lorsque la route est entièrement chargée, entraîne des problèmes de circulation et des embouteillages.
Le débit du passage à niveau peut être considérablement augmenté en amenant le passage à un état satisfaisant.