Nous implémentons et comparons 4 optimiseurs de formation de réseaux neuronaux populaires: optimiseur d'impulsion, propagation RMS, descente de gradient en mini-lots et estimation adaptative du couple. Le référentiel, beaucoup de code Python et sa sortie, les visualisations et les formules sont tous sous la coupe.

introduction

Un modèle est le résultat d'un algorithme d'apprentissage automatique s'exécutant sur certaines données. Le modèle représente ce qui a été appris par l'algorithme. C'est la «chose» qui persiste après l'exécution de l'algorithme sur les données d'apprentissage et qui représente les règles, les nombres et toute autre structure de données spécifique à l'algorithme et nécessaire à la prédiction.

Qu'est-ce qu'un optimiseur?

Avant de passer à cela, nous devons savoir ce qu'est une fonction de perte. La fonction de perte est une mesure de la mesure dans laquelle votre modèle de prédiction prédit le résultat attendu (ou la valeur). La fonction de perte est également appelée fonction de coût (plus d'informations ici ).

Pendant la formation, nous essayons de minimiser la perte de fonction et de mettre à jour les paramètres pour améliorer la précision. Les paramètres du réseau neuronal sont généralement les poids de liaison. Dans ce cas, les paramètres sont étudiés au stade de la formation. Ainsi, l'algorithme lui-même (et les données d'entrée) ajuste ces paramètres. Plus d'informations peuvent être trouvées ici .

Ainsi, l'optimiseur est une méthode pour obtenir de meilleurs résultats, contribuant à accélérer l'apprentissage. En d'autres termes, il s'agit d'un algorithme utilisé pour modifier légèrement des paramètres tels que les poids et les taux d'apprentissage pour que le modèle fonctionne correctement et rapidement. Voici un aperçu de base des différents optimiseurs utilisés dans l'apprentissage en profondeur et un modèle simple pour comprendre la mise en œuvre de ce modèle. Je recommande vivement de cloner ce référentiel et d'apporter des modifications en observant les modèles de comportement.

Quelques termes couramment utilisés:

Propagation arrière

Les objectifs de la rétropropagation sont simples: ajuster chaque poids du réseau en fonction de sa contribution à l'erreur globale. Si vous réduisez de manière itérative l'erreur de chaque poids, vous vous retrouvez avec une série de poids qui donnent de bonnes prédictions. Nous trouvons la pente de chaque paramètre pour la fonction de perte et mettons à jour les paramètres en soustrayant la pente (plus d'infos ici ).

Descente graduelle

La descente de gradient est un algorithme d'optimisation utilisé pour minimiser une fonction en se déplaçant de manière itérative vers la descente la plus raide, définie par une valeur de gradient négative. En apprentissage profond, nous utilisons la descente de gradient pour mettre à jour les paramètres du modèle (plus d'informations ici ).

Hyperparamètres

Un hyperparamètre de modèle est une configuration externe au modèle, dont la valeur ne peut être estimée à partir des données. Par exemple, le nombre de neurones cachés, le taux d'apprentissage, etc. Nous ne pouvons pas estimer le taux d'apprentissage à partir des données (plus d'informations ici ).

Taux d'apprentissage

Le taux d'apprentissage (α) est un paramètre de réglage dans l'algorithme d'optimisation qui détermine la taille du pas à chaque itération tout en se déplaçant vers le minimum de la fonction de perte (plus d'informations ici).

Optimiseurs populaires

Voici quelques-uns des référenceurs les plus populaires:

Descente de gradient stochastique (SGD).
Optimiseur de momentum.
Propagation quadratique moyenne (RMSProp).
Estimation adaptative du couple (Adam).

Examinons chacun d'eux en détail.

1. Descente de gradient stochastique (en particulier mini-batch)

Nous utilisons un exemple à la fois pour entraîner le modèle (en pure SGD) et mettre à jour le paramètre. Mais nous devons en utiliser un autre pour la boucle. Cela prendra beaucoup de temps. Par conséquent, nous utilisons des mini-lots SGD.

La descente de gradient par lots mini cherche à équilibrer la robustesse de la descente de gradient stochastique et l'efficacité de la descente de gradient par lots. Il s'agit de l'implémentation la plus courante de la descente de gradient utilisée dans l'apprentissage profond. Dans le mini batch SGD, lors de la formation du modèle, nous prenons un groupe d'exemples (par exemple, 32, 64 exemples, etc.). Cette approche fonctionne mieux car elle ne prend qu'une seule boucle pour le minibatch, pas tous les exemples. Les mini-packages sont sélectionnés au hasard pour chaque itération, mais pourquoi? Lorsque des mini-paquets sont sélectionnés au hasard, alors lorsqu'ils sont bloqués dans des minimums locaux, certaines étapes bruyantes peuvent conduire à la sortie de ces minimums. Pourquoi avons-nous besoin de cet optimiseur?

Le taux de mise à jour des paramètres est plus élevé que dans la simple descente de gradient par lots, ce qui permet une convergence plus fiable en évitant les minima locaux.
Les mises à jour par lots fournissent au processus un calcul plus efficace que la descente de gradient stochastique.
Si vous avez peu de RAM, les mini-packages sont la meilleure option. Le traitement par lots est efficace en raison de l'absence de toutes les données d'apprentissage dans la mémoire et les implémentations d'algorithmes.

Comment générer des mini-paquets aléatoires?

def RandomMiniBatches(X, Y, MiniBatchSize):

    m = X.shape[0]  
    miniBatches = [] 
   
    permutation = list(np.random.permutation(m))
    shuffled_X = X[permutation, :]
    shuffled_Y = Y[permutation, :].reshape((m,1))   #sure for uptpur shape

    num_minibatches = m // MiniBatchSize 
    for k in range(0, num_minibatches):
        miniBatch_X = shuffled_X[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch_Y = shuffled_Y[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    #handeling last batch
    if m % MiniBatchSize != 0:
        # end = m - MiniBatchSize * m // MiniBatchSize
        miniBatch_X = shuffled_X[num_minibatches * MiniBatchSize:, :]
        miniBatch_Y = shuffled_Y[num_minibatches * MiniBatchSize:, :]

        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    return miniBatches

Quel sera le format du modèle?

Je donne un aperçu du modèle au cas où vous êtes nouveau dans l'apprentissage profond. Cela ressemble à quelque chose comme ceci:

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 64)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)             #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                          #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob)  #BACKWARD PROPAGATION 
            params = update_params(params, grad, beta=0.9,learning_rate=learning_rate)
    return params

Dans la figure suivante, vous pouvez voir qu'il y a d'énormes fluctuations dans SGD. Le mouvement vertical n'est pas nécessaire: nous voulons seulement un mouvement horizontal. Si vous diminuez le mouvement vertical et augmentez le mouvement horizontal, le modèle apprendra plus rapidement, n'est-ce pas?

Comment minimiser les vibrations indésirables? Les optimiseurs suivants les minimisent et aident à accélérer l'apprentissage.

2. Optimiseur d'impulsion

Il y a beaucoup d'hésitation en SGD ou en descente de gradient. Vous devez avancer, pas de haut en bas. Nous devons augmenter le taux d'apprentissage du modèle dans la bonne direction et nous le ferons avec l'optimiseur d'élan.

Comme vous pouvez le voir sur l'image ci-dessus, la ligne verte de l'optimiseur d'impulsions est plus rapide que les autres. L'importance d'apprendre rapidement peut être vue lorsque vous avez de grands ensembles de données et de nombreuses itérations. Comment implémenter cet optimiseur?

La valeur normale de β est d'environ 0,9. Vous

pouvez voir que nous avons créé deux paramètres - vdW et vdb - à partir des paramètres de rétropropagation . Considérons la valeur β = 0,9, alors l'équation prend la forme:

vdw= 0.9 * vdw + 0.1 * dw
vdb = 0.9 * vdb + 0.1 * db

Comme vous pouvez le voir, vdw dépend davantage de la valeur précédente de vdw que de dw. Lorsque le rendu est un graphique, vous pouvez voir que l'optimiseur d'élan prend en compte les gradients passés pour lisser la mise à jour. C'est pourquoi il est possible de minimiser les fluctuations. Lorsque nous avons utilisé SGD, le chemin emprunté par la descente de gradient en mini-batch a oscillé vers la convergence. L'optimiseur Momentum aide à réduire ces fluctuations.

def update_params_with_momentum(params, grads, v, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):

        # HERE WE COMPUTING THE VELOCITIES 
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
        
        #updating parameters W and b
        params["W" + str(l + 1)] = params["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        params["b" + str(l + 1)] = params["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
    return params

Le référentiel est ici

3. Écart quadratique moyen

La propagation quadratique moyenne des racines (RMSprop) est une moyenne en décroissance exponentielle. La propriété essentielle de RMSprop est que vous n'êtes pas limité à la seule somme des dégradés passés, mais vous êtes plus limité aux dégradés des derniers pas de temps. RMSprop contribue à la moyenne exponentielle décroissante des «gradients carrés» passés. Dans RMSProp, nous essayons de réduire le mouvement vertical en utilisant la moyenne, car ils totalisent environ 0, en prenant la moyenne. RMSprop fournit la moyenne de la mise à jour.

Une source

Jetez un œil au code ci-dessous. Cela vous donnera une compréhension de base de la mise en œuvre de cet optimiseur. Tout est pareil qu'avec SGD, il faut changer la fonction de mise à jour.

def initilization_RMS(params):
    s = {}
    for i in range(len(params)//2 ):
        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return s

def update_params_with_RMS(params, grads,s, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 
        s["dW" + str(l)]= beta * s["dW" + str(l)] + (1 - beta) * np.square(grads['dW' + str(l)])
        s["db" + str(l)] = beta * s["db" + str(l)] + (1 - beta) * np.square(grads['db' + str(l)])
        
        #updating parameters W and b
        params["W" + str(l)] = params["W" + str(l)] - learning_rate * grads['dW' + str(l)] / (np.sqrt( s["dW" + str(l)] )+ pow(10,-4))
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * grads['db' + str(l)] / (np.sqrt( s["db" + str(l)]) + pow(10,-4))

    return params

4. Adam Optimizer

Adam est l'un des algorithmes d'optimisation les plus efficaces dans la formation des réseaux neuronaux. Il combine les idées de RMSProp et de Pulse Optimizer. Au lieu d'adapter le taux d'apprentissage des paramètres en fonction de la moyenne du premier moment (moyenne), comme dans RMSProp, Adam utilise également la moyenne des seconds moments des gradients. En particulier, l'algorithme calcule la moyenne mobile exponentielle du gradient et du gradient quadratique, ainsi que les paramètres beta1et beta2contrôle le taux de décroissance de ces moyennes mobiles. Comment?

def initilization_Adam(params):
    s = {}
    v = {}
    for i in range(len(params)//2 ):

        v["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        v["db" + str(i)] = np.zeros(params["b" + str(i)].shape)

        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return v, s
    
def update_params_with_Adam(params, grads,v, s, beta1,beta2, learning_rate,t):
    epsilon = pow(10,-8)
    v_corrected = {}                         
    s_corrected = {} 
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 

        v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads['dW' + str(l)]
        v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads['db' + str(l)]

        v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))


        s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.power(grads['dW' + str(l)], 2)
        s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.power(grads['db' + str(l)], 2)

        s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))

        params["W" + str(l)] = params["W" + str(l)] - learning_rate * v_corrected["dW" + str(l)] / np.sqrt(s_corrected["dW" + str(l)] + epsilon)
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * v_corrected["db" + str(l)] / np.sqrt(s_corrected["db" + str(l)] + epsilon)
    return params

Hyperparamètres

Valeur β1 (beta1) presque 0,9
β2 (beta2) - presque 0,999
ε - empêche la division par zéro (10 ^ -8) (n'affecte pas trop l'apprentissage)

Pourquoi cet optimiseur?

Ses avantages:

Implémentation simple.
Efficacité informatique.
Besoins en mémoire faibles.
Invariant à l'échelle diagonale des dégradés.
Bien adapté aux grandes tâches en termes de données et de paramètres.
Convient à des fins non stationnaires.
Convient aux tâches avec des dégradés très bruyants ou clairsemés.
Les hyperparamètres sont simples et nécessitent généralement peu de réglages.

Construisons un modèle et voyons comment les hyperparamètres accélèrent l'apprentissage

Faisons une démonstration pratique de la façon d'accélérer l'apprentissage. Dans cet article , nous ne décrirons pas les autres (initialisation, projections, forward_prop, back_prop, descente de gradient, et ainsi de suite. D.). Les fonctions requises pour la formation sont déjà intégrées à NumPy. Si vous voulez y jeter un œil, voici le lien !

Commençons!

Je crée une fonction de modèle générique qui fonctionne pour tous les optimiseurs discutés ici.

1. Initialisation:

Nous initialisons les paramètres en utilisant une fonction d'initialisation qui prend des entrées telles que features_size (dans notre cas 12288) et un tableau caché de tailles (nous avons utilisé [100,1]) et cette sortie comme paramètres d'initialisation. Il existe une autre méthode d'initialisation. Je vous encourage à lire cet article.

def initilization(input_size,layer_size):
    params = {}
    np.random.seed(0) 
    params['W' + str(0)] = np.random.randn(layer_size[0], input_size) * np.sqrt(2 / input_size)
    params['b' + str(0)] = np.zeros((layer_size[0], 1))
    for l in range(1,len(layer_size)):
        params['W' + str(l)] = np.random.randn(layer_size[l],layer_size[l-1]) * np.sqrt(2/layer_size[l])
        params['b' + str(l)] = np.zeros((layer_size[l],1))
    return params

2. Propagation vers l'avant:

Dans cette fonction, l'entrée est X, ainsi que les paramètres, l'étendue des couches cachées et la suppression, qui sont utilisés dans la technique de suppression.

J'ai mis la valeur à 1 afin qu'aucun effet ne soit vu dans l'entraînement. Si votre modèle est suréquipé, vous pouvez définir une valeur différente. Je n'applique le décrochage que sur les couches paires .

Nous calculons la valeur d'activation pour chaque couche à l'aide d'une fonction forward_activation.

#activations-----------------------------------------------
def forward_activation(A_prev, w, b, activation):
    z = np.dot(A_prev, w.T) + b.T
    if activation == 'relu':
        A = np.maximum(0, z)
    elif activation == 'sigmoid':
        A = 1/(1+np.exp(-z))
    else:
        A = np.tanh(z)
    return A


#________model forward ____________________________________________________________________________________________________________
def model_forward(X,params, L,keep_prob):
    cache = {}
    A =X

    for l in range(L-1):
        w = params['W' + str(l)]
        b = params['b' + str(l)]
        A = forward_activation(A, w, b, 'relu')
        if l%2 == 0:
            cache['D' + str(l)] = np.random.randn(A.shape[0],A.shape[1]) < keep_prob
            A = A * cache['D' + str(l)] / keep_prob
        cache['A' + str(l)] = A
    w = params['W' + str(L-1)]
    b = params['b' + str(L-1)]
    A = forward_activation(A, w, b, 'sigmoid')
    cache['A' + str(L-1)] = A
    return cache, A

3. Rétropropagation:

Ici, nous écrivons la fonction de rétropropagation. Il retournera grad ( pente ). Nous l'utilisons gradlors de la mise à jour des paramètres (si vous ne le savez pas). Je recommande de lire cet article.

def backward(X, Y, params, cach,L,keep_prob):
    grad ={}
    m = Y.shape[0]

    cach['A' + str(-1)] = X
    grad['dz' + str(L-1)] = cach['A' + str(L-1)] - Y
    cach['D' + str(- 1)] = 0
    for l in reversed(range(L)):
        grad['dW' + str(l)] = (1 / m) * np.dot(grad['dz' + str(l)].T, cach['A' + str(l-1)])
        grad['db' + str(l)] = 1 / m * np.sum(grad['dz' + str(l)].T, axis=1, keepdims=True)
        if l%2 != 0:
            grad['dz' + str(l-1)] = ((np.dot(grad['dz' + str(l)], params['W' + str(l)]) * cach['D' + str(l-1)] / keep_prob) *
                                 np.int64(cach['A' + str(l-1)] > 0))
        else :
            grad['dz' + str(l - 1)] = (np.dot(grad['dz' + str(l)], params['W' + str(l)]) *
                                       np.int64(cach['A' + str(l - 1)] > 0))

    return grad

Nous avons déjà vu la fonctionnalité de mise à jour de l'optimiseur, nous allons donc l'utiliser ici. Apportons quelques modifications mineures à la fonction de modèle à partir de la discussion sur SGD.

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    costs = []
    itr  = []

    if optimizer == 'momentum':
        v = initilization_moment(params)

    elif optimizer == 'rmsprop':
        s = initilization_RMS(params)

    elif optimizer == 'adam' :
        v,s = initilization_Adam(params)

    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 32)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)     #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                  #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob) #BACKWARD PROPAGATION 

            if optimizer == 'momentum':
                params = update_params_with_momentum(params, grad, v, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'rmsprop':
               params = update_params_with_RMS(params, grad, s, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'adam' :
                params = update_params_with_Adam(params, grad,v, s, beta1=0.9,beta2=0.999,  learning_rate=learning_rate,t=i)                                         #UPDATE PARAMETERS
            elif optimizer == "minibatch":
                params = update_params(params, grad,learning_rate=learning_rate) 

           
        
        if i%5 == 0:
            costs.append(cost)
            itr.append(i)
            if i % 100 == 0 :
                print('cost of iteration______{}______{}'.format(i,cost))
    return params,costs,itr

Entraînement avec des mini packs

params, cost_sgd,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='minibatch')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Conclusion à l'approche des mini-packages:

cost of iteration______100______0.35302967575683797 
cost of iteration______200______0.472914548745098 
cost of iteration______300______0.4884728238471557 
cost of iteration______400______0.21551100063345618
 
train_accuracy------------ 0.8494208494208494

Formation sur l'optimiseur d'impulsions

params,cost_momentum, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='momentum')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Sortie de l'optimiseur d'impulsions:

cost of iteration______100______0.36278494129038086 
cost of iteration______200______0.4681552335189021 
cost of iteration______300______0.382226159384529 
cost of iteration______400______0.18219310793752702 train_accuracy------------ 0.8725868725868726

Formation avec RMSprop

params,cost_rms,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='rmsprop')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Sortie RMSprop:

cost of iteration______100______0.2983858963793841 
cost of iteration______200______0.004245700579927428 
cost of iteration______300______0.2629426607580565 
cost of iteration______400______0.31944824707807556 train_accuracy------------ 0.9613899613899614

Entraînement avec Adam

params,cost_adam, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='adam')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Conclusion d'Adam:

cost of iteration______100______0.3266223660473619 
cost of iteration______200______0.08214547683157716 
cost of iteration______300______0.0025645257286439583 
cost of iteration______400______0.058015188756586206 train_accuracy------------ 0.9845559845559846

Avez-vous vu la différence de précision entre les deux? Nous avons utilisé les mêmes paramètres d'initialisation, le même taux d'apprentissage et le même nombre d'itérations; seul l'optimiseur est différent, mais regardez le résultat!

Mini-batch accuracy : 0.8494208494208494
momemtum accuracy   : 0.8725868725868726
Rms accuracy        : 0.9613899613899614
adam accuracy       : 0.9845559845559846

Visualisation graphique du modèle

Vous pouvez vérifier le référentiel si vous avez des doutes sur le code.

Résumé

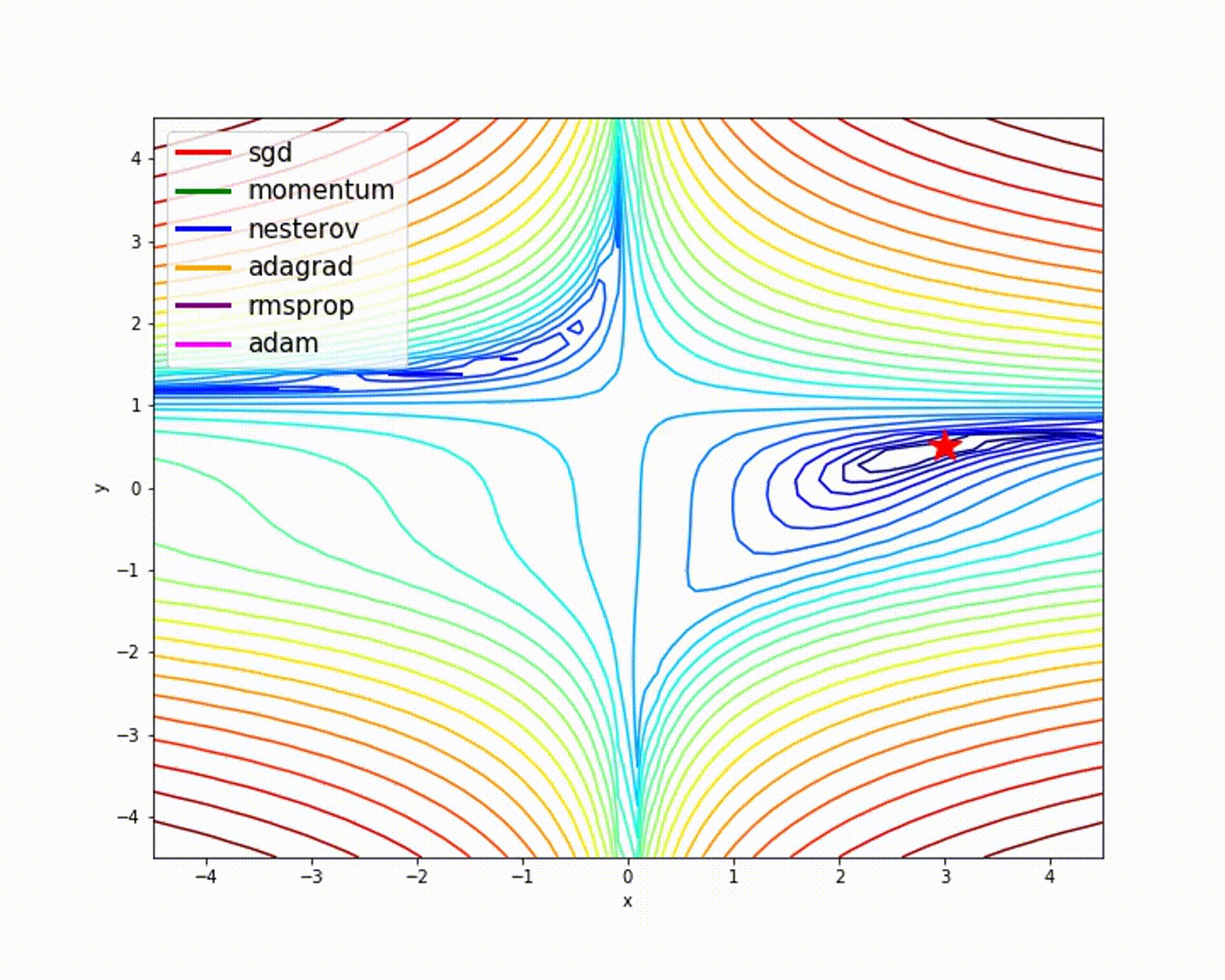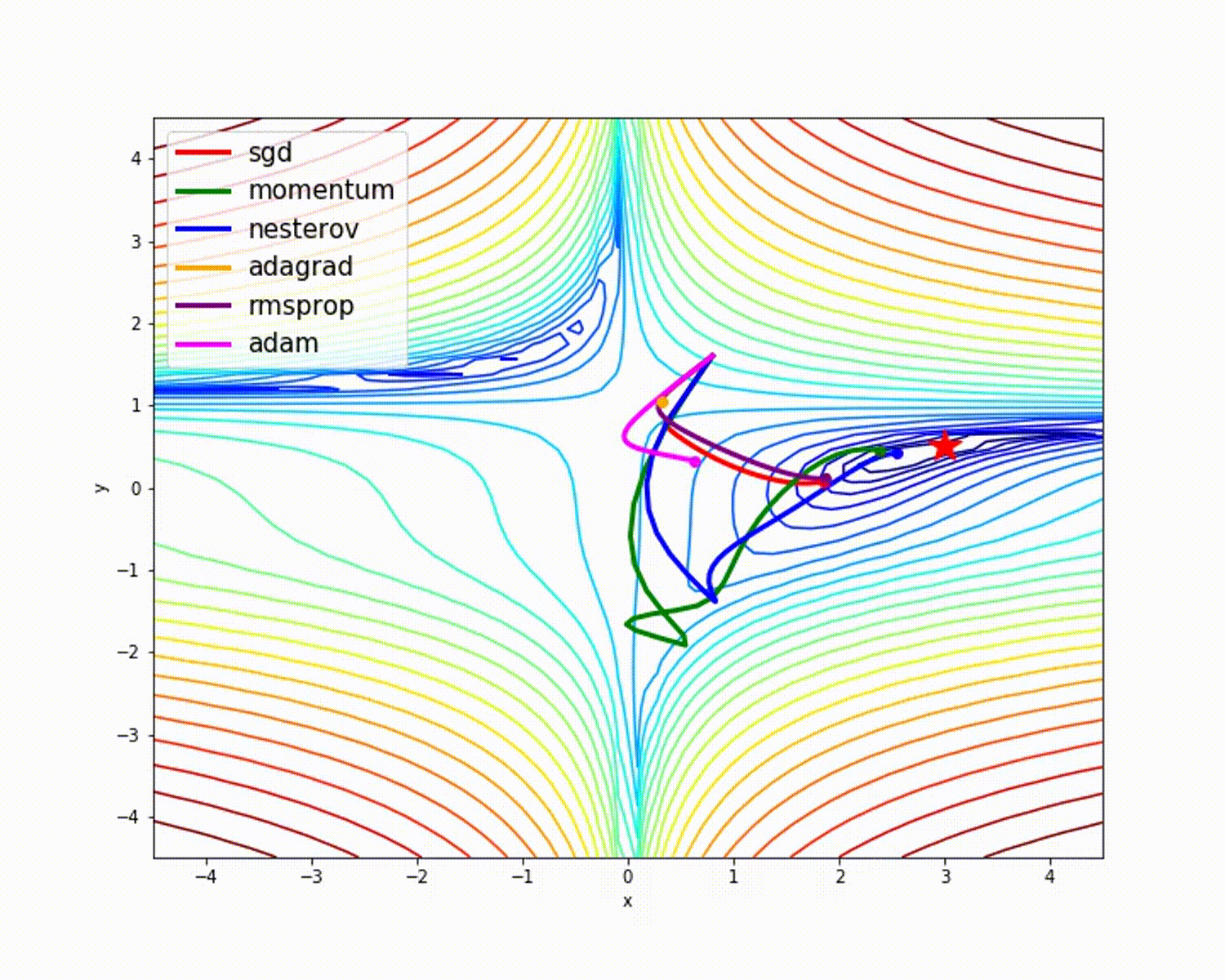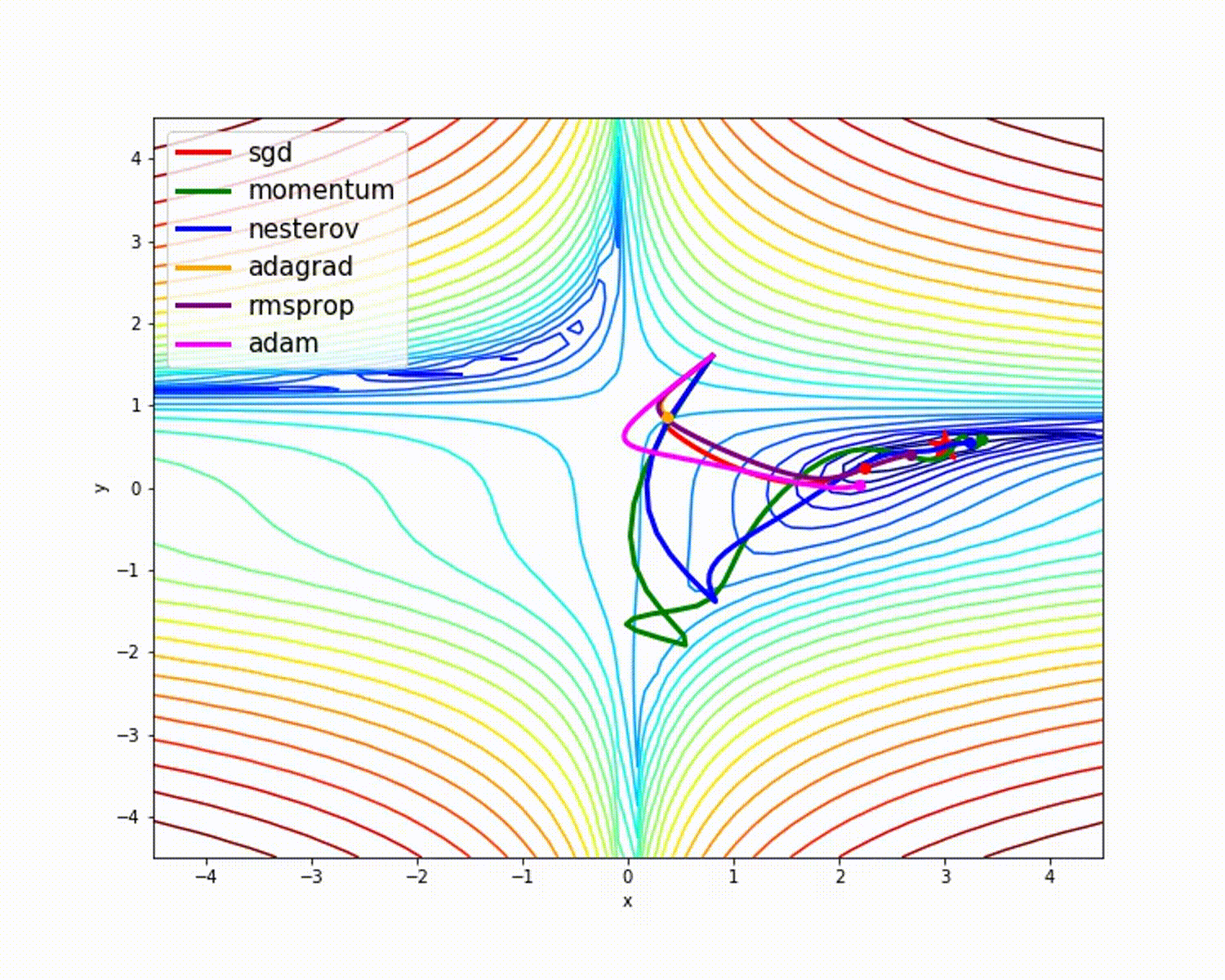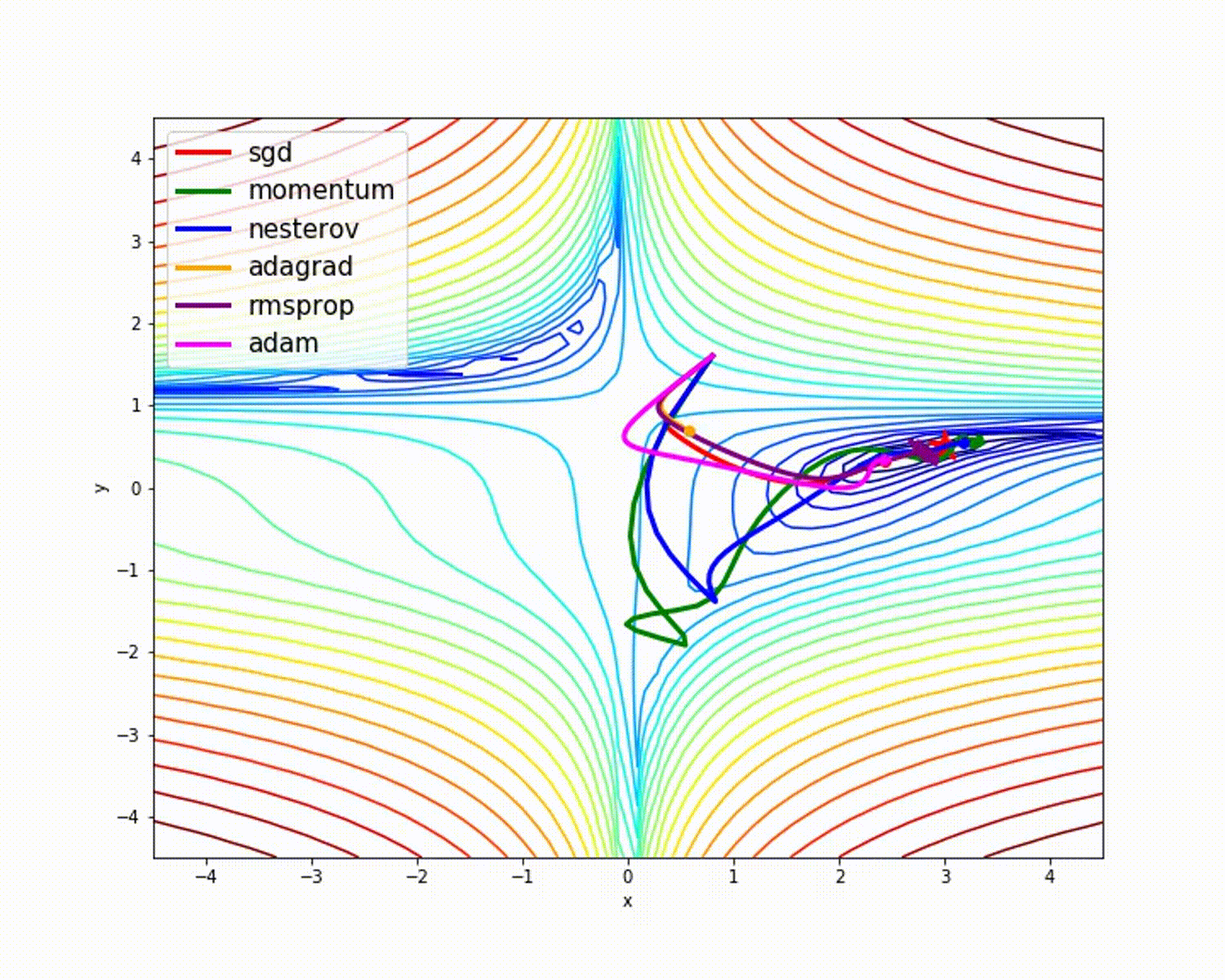
source

Comme nous l'avons vu, l'optimiseur Adam donne une bonne précision par rapport aux autres optimiseurs. L'image ci-dessus montre comment le modèle apprend par itérations. Momentum donne la vitesse SGD et RMSProp donne la moyenne exponentielle des poids pour les paramètres mis à jour. Nous avons utilisé moins de données dans le modèle ci-dessus, mais nous verrons plus d'avantages des optimiseurs lorsque nous travaillons avec de grands ensembles de données et de nombreuses itérations. Nous avons discuté de l'idée de base des optimiseurs, et j'espère que cela vous motivera à en savoir plus sur les optimiseurs et à les utiliser!

Ressources

Coursera —
—

Les perspectives des réseaux de neurones et de l'apprentissage automatique en profondeur sont énormes et, selon les estimations les plus prudentes, leur impact sur le monde sera à peu près le même que celui de l'électricité sur l'industrie au 19e siècle. Les spécialistes qui évalueront ces perspectives avant tout le monde ont toutes les chances de devenir le chef du progrès. Pour ces personnes, nous avons fait un code promo HABR , qui donne un supplément de 10% à la remise formation indiquée sur le bandeau.

Plus de cours

Implémentation et comparaison des optimiseurs de modèle dans le Deep Learning