Les systèmes réels ne peuvent être considérés comme linéaires que sur une plage limitée de charges. Le monde réel qui nous entoure n'est pas linéaire (Fig. 1). La non-linéarité est une violation du principe de superposition dans un certain phénomène (système mécanique): le résultat de l'action de la somme des facteurs n'est pas égal à la somme des résultats des facteurs individuels. Cependant, pour diverses raisons, notamment le manque des connaissances nécessaires, des compétences en modélisation et des logiciels nécessaires, les ingénieurs ne résolvent souvent les problèmes que dans des formulations linéaires. Même lorsque l'approche linéaire donne de très grosses erreurs. Une modélisation précise du comportement du système nécessite souvent une analyse non linéaire.
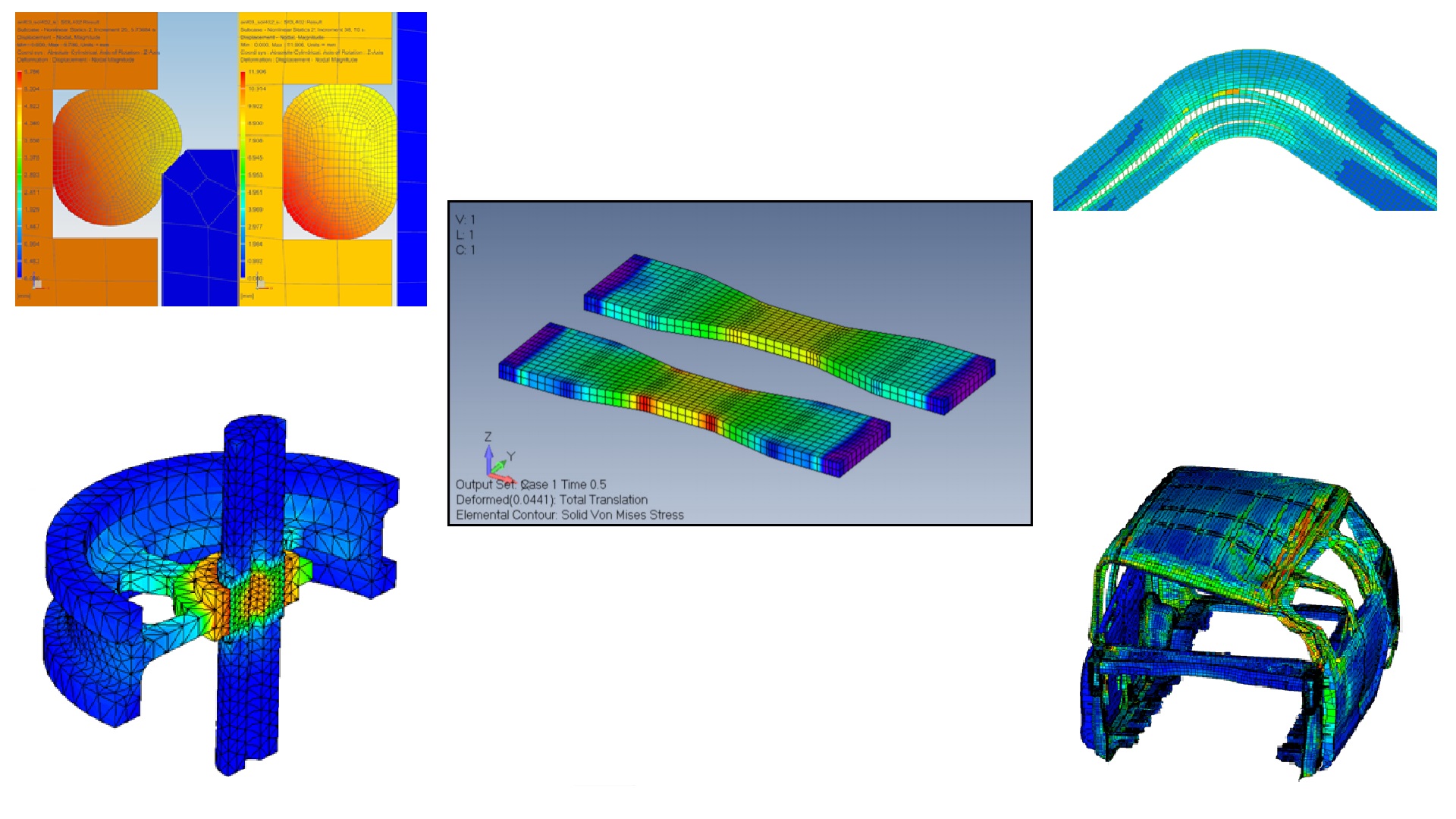
Figure: 1
introduction
Il y a quelques mois, j'ai publié un article intitulé «Just About Nonlinear Finite Element Analysis. Un exemple de parenthèse . " Dans celui-ci, j'ai essayé d'expliquer de manière accessible le minimum de termes et de théorie nécessaires à la conduite consciente de l'analyse statique non linéaire, j'ai analysé en détail l'algorithme pour résoudre un problème non linéaire simple. Je ne me répéterai pas, je vous rappellerai quelques dispositions de base - et nous procéderons à un examen des phénomènes plus complexes, des problèmes de mécanique et des outils nécessaires pour résoudre ces problèmes non linéaires.
Les hypothèses linéaires sont souvent valides, mais les calculs non linéaires sont de plus en plus nécessaires dans le développement de produits aujourd'hui. Pour réduire la quantité de tests expérimentaux, les utilisateurs ont besoin de modèles de plus grande précision: les modèles géométriques sont affinés, la précision des modèles physiques est augmentée. Cela signifie que les effets non linéaires tels que les contacts, les grandes déformations et les propriétés des matériaux sont pris en compte. La non-linéarité du problème peut être due à la nécessité de prendre en compte l'historique de chargement de la structure - c'est-à-dire que la décomposition du problème en composantes de l'impact et la combinaison ultérieure des résultats est impossible. Si ces effets ne sont pas pris en compte, les décisions peuvent être inexactes, conduisant à des conclusions erronées. Ou bien, les produits peuvent être conçus avec de très grandes marges de sécurité et donc devenir trop chers.
Nous avons une physique et des mathématiques classiques, mais différents systèmes de calcul utilisent différents ensembles d'algorithmes et d'outils pour résoudre des problèmes par la méthode des éléments finis. Dans cet article, je vais parler des outils disponibles dans le pré-post-processeur Femap avec le solveur NX Nastran, qui s'est avéré fiable, précis et rapide depuis 35 ans. Pour résoudre les problèmes non linéaires les plus complexes, y compris s'il est nécessaire de prendre en compte l'historique de chargement d'une structure, le module de solution non linéaire multi-étapes non linéaire Multistep (SOL401 / SOL402) convient.
Contacts et utilisation des sous-cas
Dans une seule solution en plusieurs étapes, vous pouvez modifier les conditions de contact des surfaces à l'aide de sous-cas . Les sous-cas sont des solutions distinctes à partir desquelles vous pouvez ajouter une solution générale avec un historique complexe d'application de charge, des changements dans les conditions aux limites. Par exemple, lors de la modélisation d'un assemblage, vous pouvez ajouter ou supprimer des contacts dans l'ordre.
Le frottement peut être pris en compte dans les réglages de contact, et le coefficient de frottement peut être constant ou varier avec la vitesse, la température et le temps. Les pièces en contact sont généralement considérées comme déformables. Mais si une partie est beaucoup plus rigide que l'autre, cela vaut la peine de la considérer comme rigide afin de simplifier la tâche sans erreurs significatives. Il permet également d'appliquer le mouvement forcé d'un corps rigide à une pièce rigide en tant que charge.
En figue. 2 montre un modèle dans lequel le joint torique en caoutchouc est défini par un matériau hyperélastique. La simulation calcule les contraintes et les déplacements dans le joint torique en caoutchouc utilisé pour sceller le chapeau qui est monté sur le cylindre. Afin d'améliorer l'efficacité, le modèle est construit en utilisant la symétrie axiale. Le cercle visible est la section transversale du joint torique. La bague d'étanchéité non contrainte est plus petite que le diamètre du cylindre, de sorte que la position initiale de la bague d'étanchéité indique que la bague d'étanchéité et le cylindre se chevauchent. Dans la première étape de simulation, le chevauchement est compensé pour la détermination du contact, c'est-à-dire que le joint torique est étiré radialement. Ensuite, le bouchon est abaissé et le joint torique se déforme au contact de la paroi du cylindre.Ainsi, un joint est formé.

Figure: 2 Les
imperfections géométriques du maillage par éléments finis peuvent être corrigées en ajustant les tolérances de jeu et d'interférence ou en lissant les bords. Si vous rencontrez des problèmes de convergence, il existe de nombreuses options pour résoudre ce problème. Par exemple, l'option Régularisation normale est utile lorsque les conditions de contact incluent des matériaux souples tels que le caoutchouc. La régularisation tangentielle évite les discontinuités dans les forces de frottement. De plus, la rigidité locale et l'amortissement au niveau du contact sont contrôlés par l'utilisateur, ce qui peut également être utilisé pour améliorer la convergence. Les résultats suivants peuvent être analysés dans le post-processeur: pression de contact, distance normale, glissement, forces de contact.
Il existe de nombreuses applications de contact, notamment le boulonnage, la simulation de chute et l'ajustement serré. Vous pouvez modéliser des assemblages boulonnés à l'aide d'éléments finis 1D (poutres, barres), 2D (éléments plans) ou d'éléments 3D. La pré-tension peut être effectuée avec plusieurs sous-cas - par exemple, si vous souhaitez simuler une séquence de serrage de boulons. Les sous-cas de prétension peuvent être implémentés non seulement en premier dans une ligne, mais également dans n'importe quelle séquence. Lors de l'analyse d'autres sous-cas, les précontraintes calculées sont conservées, mais la charge réelle du boulon peut changer avec l'application ultérieure des charges. Les utilisateurs peuvent analyser les contraintes normales, les contraintes de cisaillement, les moments des boulons - tout au long de la solution.
En figue. 3 représente un modèle pour analyser la séquence d'assemblage / chargement / déchargement suivante: serrez le boulon # 1, serrez le boulon # 4, serrez le boulon # 2, serrez le boulon # 3, appliquez la charge de service, retirez la charge, relâchez.

Figure: 3
Grands déplacements (déformations) et analyse après flambage
Les grands déplacements linéaires et angulaires sont des effets non linéaires fondamentaux (figure 4). Ils prennent en compte le changement de position de charge lorsque le système se déforme. Il y a aussi pour effet de changer la rigidité du produit par rapport à la charge. La solution de flambement est une solution non linéaire avec des effets de déformation importants activés.
La charge entraîne une perte de rigidité du produit, conduisant à de grandes déformations ultérieures avec de petites modifications de la charge. Des algorithmes efficaces existent pour analyser le système après le dépassement de la charge critique de flambement.

Figure: 4
Analyse après flambageEst un type spécial de sous-cas statique dans Femap. Dans l'analyse quasi-statique standard, les charges sont augmentées selon une loi définie par l'utilisateur. Cependant, certains produits sont instables en raison de leur forme après avoir atteint un certain niveau de charge. Ces produits perdent brutalement leur rigidité dans une certaine plage de charges. Pour résoudre ce genre de problèmes, l'algorithme de "longueur d'arc" doit être utilisé - il est utilisé pour résoudre les problèmes de flexion instable, de perte de stabilité. La solution permet non seulement de déterminer la charge critique de flambement en flexion, mais aussi d'analyser le comportement de la structure après qu'elle soit devenue instable. Au lieu de changer les charges en fonction des incréments de temps, l'algorithme modifie automatiquement les incréments de charge proportionnellement au déplacement et non au temps.
Les imperfections initiales de la forme ont une grande influence sur les problèmes de flambage. Les imperfections de forme peuvent être considérées comme des distorsions dans la géométrie / maillage, qui peuvent être utilisées pour tenir compte des imperfections dans le processus de fabrication. L'utilisateur peut simuler les endroits de flexion délibérée ou simuler les dommages reçus pendant le fonctionnement.
Non-linéarité physique (non-linéarité des propriétés du matériau). Plasticité, hyperélasticité, ténacité, fluage et composites
Dans l'analyse linéaire traditionnelle, tous les matériaux sont considérés comme linéaires et élastiques. Le solveur non linéaire à étapes multiples Femap prend en charge les propriétés non linéaires ainsi que le comportement isotrope, orthotrope et anisotrope. Plusieurs autres modèles de comportement de matériaux non linéaires sont également pris en charge, notamment la plasticité, l'hyperélasticité, le fluage et les dommages. Les utilisateurs qui ont besoin de définir des propriétés de matériau uniques ont la possibilité d'ajouter éventuellement leurs propres modèles de matériaux.
Modèles en matière plastiqueavec différents paramètres sont disponibles pour la simulation. Les utilisateurs peuvent définir la courbe contrainte-déformation comme bilinéaire ou multilinéaire (Figure 5). Les effets de chargement / déchargement peuvent être décrits à l'aide de modèles d'écrouissage isotropes, cinématiques ou mixtes. Les courbes de contrainte-déformation peuvent également être complétées par une dépendance à la température. Ainsi, les matériaux, dont la dépendance des propriétés de la température doit être prise en compte lors de la résolution du problème, peuvent être décrits de manière adéquate.

Figure: 5
matériaux hyperélastiquesen raison de leurs propriétés, ils sont largement utilisés dans diverses industries. Ils sont indépendants de la vitesse de déformation. Ces matériaux comprennent le caoutchouc, la mousse, les matériaux biologiques et polymères. Ils supportent de très grandes déformations (plus de 600%), sont pratiquement incompressibles et peuvent également dépendre de la température. Des modèles de matériaux standard de Mooney-Rivlin, Ogden avec effet Mullins et des modèles en mousse sont disponibles. En figue. 6 montre un modèle du couvercle du pommeau de levier de vitesses. Le matériau de protection est spécifié comme un matériau en caoutchouc hyperélastique en utilisant le modèle Mooney-Rivlin. Les surfaces du boîtier sont configurées pour un contact automatique.

Figure: 6
Les matériaux viscoélastiques sont des matériaux élastiques qui ont la capacité de dissiper l'énergie mécanique en raison de l'influence de la viscosité.
Les matériaux élastiques tels que le caoutchouc s'étirent instantanément et reviennent rapidement à leur état d'origine lorsque la charge est retirée. La viscosité (frottement interne) est la propriété d'un corps de résister au mouvement d'une partie de celui-ci par rapport à une autre. Femap prend en charge les matériaux viscoélastiques avec les formulations des séries Kelvin et Prony. Le modèle Kelvin reflète le phénomène de séquelle élastique, qui est une modification de la déformation élastique au fil du temps, lorsqu'elle augmente constamment jusqu'à une certaine limite après l'application de la charge, ou diminue progressivement après son retrait (Fig.7). Lorsque la tension est relâchée, le matériau se détend progressivement jusqu'à un stade non déformé. Le modèle Kelvin est utilisé pour les polymères organiques, le caoutchouc, le bois à faible contrainte.

Figure: 7
Déformations de type fluagese produisent au fil du temps sans aucun changement de charge. La déformation au fluage, comme en plasticité, est irréversible (inélastique), le comportement du matériau au fluage est incompressible.
De nombreux matériaux, en particulier dans des conditions de température élevée, peuvent subir des déformations par fluage. Femap utilise le modèle de fluage Bailey-Norton standard et vous permet de définir les dépendances de température pour les facteurs déterminants.
Dans la plupart des matériaux, sous l'action d'une charge constante, on distingue trois étapes de fluage (Fig.8). Dans la première étape, la vitesse de déformation diminue avec le temps. Ce phénomène est observé pendant une courte période de temps. Le deuxième étage, plus long, se caractérise par une vitesse de déformation constante. Au troisième stade, la vitesse de déformation augmente rapidement jusqu'à la destruction complète du matériau (rupture de l'échantillon).

Figure: 8 Le
solveur non linéaire à plusieurs étapes Femap peut simuler le comportement non linéaire des composites résultant d'une fracture intercouche ou intercouche (Figure 9).
Dans le cas d'une destruction intra-couche, les couches individuelles s'affaiblissent et perdent leur rigidité lorsqu'un certain niveau de charge est dépassé. Le solveur surveille la rigidité de chaque couche de l'assemblage et met à jour la rigidité de la fonction à mesure que les couches sont plus endommagées. Dans les cas extrêmes, une perte complète de rigidité de l'élément peut se produire. Les fractures intra-couches (pour une couche unidirectionnelle ou tissée) sont de natures diverses: destruction des fibres, destruction de la matrice, destruction des liaisons entre la matrice et les fibres.
Avec la destruction de la couche intermédiaire, la liaison entre les couches du produit peut s'affaiblir et perdre sa rigidité. Femap utilise des liants pour modéliser ce comportement. La simulation montre les zones où la liaison est perdue et les couches peuvent être détachées.

Figure: neuf
Comptabilité de l'historique des charges. Solutions en plusieurs étapes utilisant des sous-cas
L'état de la structure dépend dans certains cas de la séquence d'application des charges, c'est-à-dire que la non-linéarité du problème peut être due à la nécessité de prendre en compte l'historique de chargement de la structure. Il existe des problèmes dans lesquels il suffit de prendre en compte l'état initial contrainte-déformation (souvent pour des non-linéarités liées au comportement du matériau). Mais parfois, il est nécessaire de prendre en compte un historique de chargement complexe, composé de plusieurs sous-cas avec des facteurs de force et des conditions aux limites variables. Les conditions aux limites peuvent changer lorsque les zones de contact changent.
Une caractéristique importante du solveur non linéaire à plusieurs étapes Femap est qu'il peut prendre en charge plusieurs sous-cas et exécuter différentes solutions - telles que statique, dynamique, modale dans des sous-cas séparés au sein d'une même solution. En plus de modifier le type d'analyse dans les sous-cas, vous pouvez également modifier les paramètres des paramètres et les conditions aux limites. Cela donne aux utilisateurs une grande flexibilité dans la personnalisation de leurs solutions. Voici un scénario typique utilisant des sous-cas: chaque sous-cas commence par les conditions dans lesquelles le sous-cas précédent s'est terminé. Ce sous-cas est appelé séquentiel. Mais l'utilisateur peut également redémarrer la solution et non dans un sous-cas séquentiel.
En figue. La figure 10 montre un exemple de modélisation de trois composants d'un moteur d'aéronef: deux flasques et un moyeu sont boulonnés ensemble en plusieurs étapes. Pour une solution efficace, un secteur symétrique du modèle est utilisé. Dans un premier temps, les écarts par rapport au moule pour une bride et un moyeu sont analysés. Sur le second, deux boulons sont serrés pour relier la bride et le moyeu. Le troisième examine le pressage de la deuxième bride. Sur le quatrième, deux autres boulons sont serrés pour connecter la deuxième bride au moyeu. Ensuite, dans la cinquième étape, la charge de la rotation à grande vitesse des pièces entièrement connectées est analysée. La dernière étape est l'analyse modale - elle est utilisée pour prédire les contraintes de vibration. Cet ensemble complet de six étapes peut être réalisé en une seule analyse,qui fournit un riche ensemble de données pour comprendre l'état de contrainte-déformation du moteur.

Figure: 10
En plus des sous-cas statiques, les cas dynamiques (transitoires) sont pris en charge. Ce type de sous-cas peut démarrer une solution ou suivre un sous-cas statique (Figure 11). Lors de l'exécution de la solution, des conditions initiales sous forme de déplacement ou de vitesse peuvent être appliquées. Par exemple, pour simuler une chute, il est rationnel de démarrer la solution à partir d'un point immédiatement avant l'impact et de définir la vitesse initiale égale à la vitesse d'impact. Si l'analyse dynamique suit une analyse statique ou une autre analyse dynamique, alors les écarts, vitesses, accélérations au début du sous-cas seront les mêmes qu'à la fin du sous-cas précédent.
Dans un sous-cas dynamique, les forces d'inertie générées, l'amortissement, la matrice de rigidité et les forces sont équilibrés par les charges appliquées. Les forces d'inertie peuvent être désactivées pendant l'analyse transitoire. Ceci est très utile pour accélérer la solution et passer à un état stable.

Figure: Onze
Analyse dynamique et modélisation des liens cinématiques
Des simulations de chute sont souvent effectuées sur des appareils électroniques pour voir dans quelle mesure ils survivront à une collision avec le sol. En figue. 12 montre le processus de choc qui se produit lorsqu'une caméra thermique tombe. Le matériau du boîtier en polycarbonate est modélisé comme un matériau élastoplastique, tandis que le PCB interne et les composants électroniques sont modélisés comme des matériaux élastiques linéaires. L'analyse dynamique commence au point de contact de la caméra thermique avec le sol. La caméra reçoit une vitesse initiale correspondant à la hauteur à partir de laquelle elle a été larguée (dans ce cas, elle est de 1 mètre). La caméra touche rapidement le sol et rebondit. Les contraintes et déformations de la coque et des flancs sont analysées.

Figure: 12
Femap prend en charge l' utilisation de contraintes cinématiquespour connecter différentes parties de l'assemblage. Les types de charnières de base sont pris en charge tels que les guides cylindriques, sphériques, rigides et flexibles.
En figue. 13 représente le processus de déploiement de panneaux solaires sur un satellite relié par une charnière cylindrique. Avec ce modèle, les vibrations et les niveaux de contraintes peuvent être estimés.

Figure: 13
Conclusion
Les principaux critères de qualité pour évaluer le modèle de conception et les résultats obtenus ont toujours été et seront la comparaison avec des expériences de terrain et des solutions analytiques. Les modèles non linéaires n'échappent pas à la règle. Les développeurs Femap de Siemens valident les formulations non linéaires à l'aide de tests et de solutions analytiques NAFEMS (International Association for Analysis and Modeling Engineering).
En plus de la vérification de la formulation, les algorithmes sont régulièrement testés à l'aide d'une grande bibliothèque de modèles de test pour éviter les bogues au fur et à mesure que des améliorations et des extensions sont ajoutées.
Cependant, chaque ingénieur est confronté à la question de l'adéquation des hypothèses formulées, de la bonne utilisation des outils logiciels disponibles et de l'évaluation multicritères des résultats obtenus.
Cet article fournit une vue d'ensemble des problèmes non linéaires actuels et des outils pour leur solution. Bien entendu, ces informations ne sont pas suffisantes pour commencer à résoudre les problèmes ci-dessus dans la pratique. Par conséquent, je vous invite à un webinaire gratuit "Femap et les capacités du module de solutions non linéaires multi-étapes Multistep Nonlinear" , qui se tiendra le 19 novembre 2020 à 12h00. Dans la seconde moitié du webinaire, je résoudrai le problème de l'étirement d'un échantillon de métal, en tenant compte de la plasticité et du durcissement isotrope du matériau. Vous pouvez lire un aperçu des capacités du complexe de calcul Femap avec NX Nastran ici , et télécharger une version d'essai gratuite de Femap avec NX Nastran ici . Philip Titarenko, chef de produit Femap

JSC Nanosoft
E-mail: titarenko@nanocad.ru
Références
1. Femap avec NX Nastran, Solveurs non linéaires Simcenter 3D Multistep: SOL401 / SOL402.Multistep Nonlinear (traduit par F.V. Titarenko). Siemens.
2. NX Nastran Handbook of Nonlinear Analysis (Solutions 106 et 129). Siemens.