une épigraphe, Google / Yandex n'a pas trouvé l'auteur
C'est la deuxième partie de l' article «Ce qui est clair pour tout le monde».
Pour une meilleure compréhension de l'algorithme Z décrit dans celui-ci, j'ajouterai ici un bon exemple donné plus tôt dans la discussion / commentaires.
Imaginons que la tâche consiste à construire une courbe d'une fonction T (X) sur un intervalle donné de valeurs (permises). Il est souhaitable de le faire avec le plus de détails possible, mais vous ne savez pas à l'avance quand vous serez «saisi par la main». Vous souhaitez générer des valeurs X afin qu'à tout moment lorsque le tracé de la courbe est interrompu (génération de paramètres X sur un intervalle et calcul de T (X)), le graphique résultant reflète cette fonction aussi précisément que possible. Cela prendra plus de temps - le graphe sera plus précis, mais - toujours le maximum de ce qui est possible pour le moment pour une fonction arbitraire .
Bien entendu, pour une fonction connue, l'algorithme de partitionnement par intervalles peut prendre en compte son comportement, mais il s'agit ici d'une approche générale qui donne le résultat souhaité avec des «pertes» minimales. Pour un cas bidimensionnel, vous pouvez donner un exemple d'affichage d'un certain relief / surface et voulez être sûr que, dans la mesure du possible, vous avez affiché le maximum de ses caractéristiques.
La tâche et les objets de la modélisation (à partir de la première partie) dans le cas général peuvent être très différents: il y a un modèle théorique / physique ou une approximation ou non (boîte noire) - il y aura des nuances dans la construction de modèles partout. Mais la nécessité de générer des paramètres (y compris l'algorithme Z) est une partie commune et intégrale pour tout le monde. Il y a des objets (par exemple, tels que ) lorsque le temps d'obtention de T est trop long (jours et semaines), alors l'algorithme de choix d'une nouvelle étape s'arrête par d'autres critères, pas à cause de l'achèvement du cycle de calcul principal dans un processus parallèle. Cela n'a aucun sens de diminuer davantage l'étape pour améliorer la recherche de la prochaine prévision T si l'amélioration attendue est évidemment pire que l'erreur de modèle et / ou les erreurs de mesure T.
Je donnerai encore une illustration de la division de l'intervalle admissible pour le cas bidimensionnel de l'algorithme Z (K = 3 dans le champ 64 * 64):

Les points mis en évidence sur la figure (9 pcs.) Sont les points de départ des arêtes et le milieu de l'intervalle, ils sont, si nécessaire, considérés en dehors de l'algorithme Z. Vous pouvez voir que le long des directions horizontale et verticale / "chemins" reliant ces points générés par l'algorithme Les valeurs Z sont manquantes. Les points supplémentaires ici sont faciles à calculer séparément, mais avec une augmentation du nombre de points le long de ces directions / «chemins», la représentation de la fonction s'améliorera (les «chemins» deviendront plus étroits) et la nécessité de compléter l'algorithme lui-même (7 lignes sont nécessaires, dont 4 opérateurs dans la boucle principale en n, voir ci-dessous) ou je ne vois pas la création d'un calcul séparé. De plus, dans ce cas, le rendement moyen de l'algorithme se détériore, et il n'y aura pas d'amélioration particulière dans la représentation du modèle (même pour n> 8, le pas dans le paramètre est inférieur à 1/1000, voir le tableau ci-dessous).
La deuxième caractéristique de l'algorithme Z est (pour le cas bidimensionnel) l'asymétrie dans l'ordre d'addition des points - ils sont plus fréquents sur l'axe / paramètre Y, l'image est alignée à la fin de chaque cycle par n.
Algorithme Z, cas unidimensionnel, en langage VBA:
Xmax =
Xmin =
Dx = (Xmax - Xmin) / 2
L = 2
Sx = 0
For n = 1 To K
Dx = Dx / 2
D = Dx
For j = 1 To L Step 2
X = Xmin + D
Cells(5, X) = "O" ' - / T(X)
X = Xmax - D
Cells(5, X) = "O"
D = D + Sx
Next j
Sx = Dx
L = L + L
Next nAlgorithme Z, cas 2D, langage VBA:
Xmax = ' 65 - , GIF
Xmin = ' 1
Ymax = ' 65
Ymin = ' 1
Dx = (Xmax - Xmin) / 2
Dy = (Ymax - Ymin) / 2
L = 2
Sx = 0
Sy = 0
For n = 1 To K ' K = 3 GIF
Dx = Dx / 2
Dy = Dy / 2
Tx = Dx
For j = 1 To L Step 2
X1 = Xmin + Tx
X2 = Xmax - Tx
Ty = Dy
For i = 1 To L Step 2
Y = Ymin + Ty
Cells(Y, X1) = "O" ' - / T(Y,X)
Cells(Y, X2) = "O"
Y = Ymax - Ty
Cells(Y, X1) = "O"
Cells(Y, X2) = "O"
Ty = Ty + Sy
Next i
Tx = Tx + Sx
Next j
Sx = Dx
Sy = Dy
L = L + L
Next nCoûts de calcul:
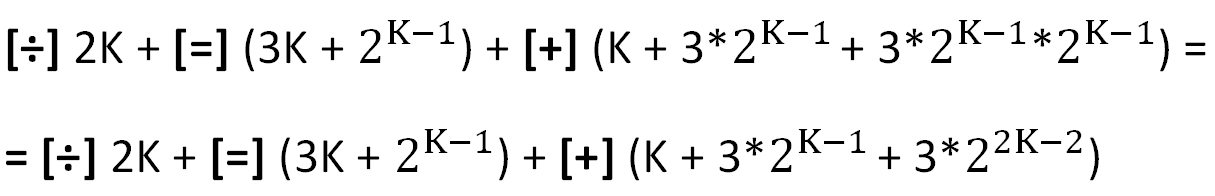
Les principales opérations utilisées dans les calculs sont indiquées entre crochets (les coûts d'organisation des cycles ne sont pas pris en compte).
Il faut noter ici que l'opération plutôt "lourde" de division [÷] dans ce cas n'est pas coûteuse, car la division entière par 2 est un décalage d'un chiffre. Les coûts relatifs de l'opération de division et d'affectation ([=], deuxième terme) tendent rapidement à zéro lorsque K.
Total des points:

Coûts moyens:

Pour les premières valeurs de K, nous effectuerons des calculs à l'aide de ces formules et remplirons le tableau:

Ici "fraction de l'intervalle" est le pas relatif entre les points en fin de cycle de n.
La dernière ligne («moyenne») montre le coût relatif par point - la proportion d'ajouts / soustractions. La limite tend vers 0,5625 ou 1 / 1,77777 de l'opération d'addition.
Revenant à l'assertion de la première partie de l'article , il est montré ici que «l'algorithme proposé pour discussion démontre des coûts de calcul extrêmement faibles et n'entraîne aucun inconvénient ou difficulté», et dans des conditions d'interruption brutale des calculs, il présente en outre des avantages. Il est judicieux de l'utiliser dans toutes les applications appropriées.
Je demande de l'aide pour distribuer et mettre en œuvre des logiciels et du matériel.