Il y a un fait tellement mystérieux à propos des transformations linéaires: certaines d'entre elles, à savoir la mise à l'échelle et la translation non uniformes, distinguent pour une raison quelconque entre les vecteurs «ordinaires» et les normales. Lorsque nous transformons un vecteur "normal" par une matrice, alors les normales pour une raison quelconque doivent être transformées par une matrice transposée inverse. Comment comprendre cela?

À l'aide de calculs simples, vous pouvez vous assurer que la matrice transposée inverse préserve la perpendicularité des normales à ses plans tangents. Dans une certaine mesure, cette preuve est suffisante, mais elle manque une histoire plus profonde et plus intéressante sur la géométrie derrière tout cela. C'est l'histoire que je veux raconter dans les prochains articles.

Unités et mise à l'échelle

Voici un bref aperçu avant de plonger dans le cœur de l'article. Considérez la bonne vieille mise à l'échelle uniforme (un facteur sur tous les axes). Il est difficile de penser à une transformation plus inoffensive - c'est juste la multiplication de tous les vecteurs par le même nombre.

Mais à y regarder de plus près, quelque chose de pas entièrement insignifiant se passe ici. Certaines quantités comportent des «dimensions» ou des «unités» physiques telles que des longueurs, des surfaces et des volumes. Lors de la mise à l'échelle, ces valeurs changent en fonction de leurs unités. Certaines valeurs sont généralement «sans dimension» et ne changent pas lorsqu'elles sont mises à l'échelle.

À titre d'exemple, listons tous les comportements d'unité possibles lors de la mise à l'échelle dans l'espace 3D. Nous désignons le facteur d'échelle comme$$$a>0$ . Ensuite:

• Les nombres sans dimension ne changent pas, en d'autres termes, ils sont multipliés par$$$a^0$ .
• Les longueurs sont multipliées par$$$a$ .
• Les surfaces sont multipliées par$$$a^2$ .
• $$$a^3$.
  
  : , :
• $$$1\over{a}$.
• $$$1\over{a^2}$.
• $$$1\over{a^3}$.
  
  , , . 3D- , , , .

, ( ) , : , ( ), , - . , -3 3. , $$$k$- , $$$a^k$.

( $$$\pm 4$ , . , 3D.)

, - . ? ? ? -, .

, . , . , Geometric Algebra for Computer Science. .

— , , , , . $$$k$-, $$$k$ — . , — . .

— ( ) , . , , . , .

, , . , . , . , , , .



, — , , . , , , , .

. , , . , , "" "", "" "". , , .

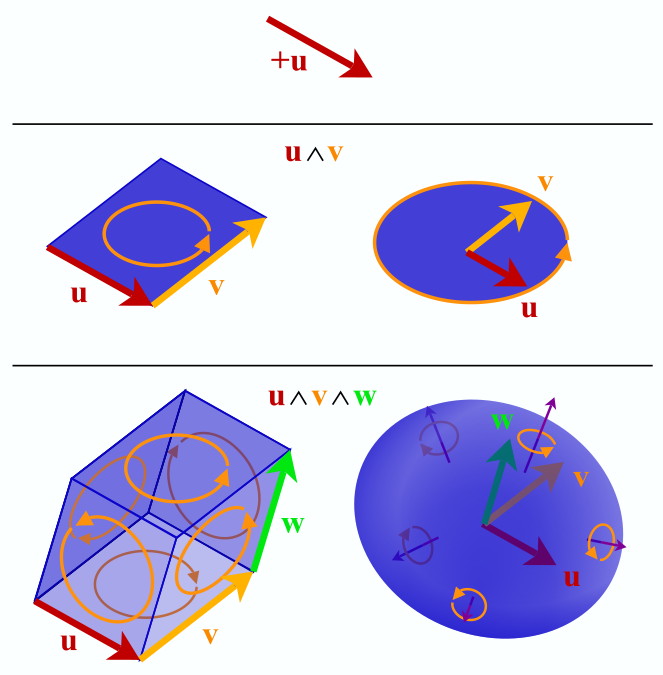
́ , . , $$$k$- . .

$$$k$-

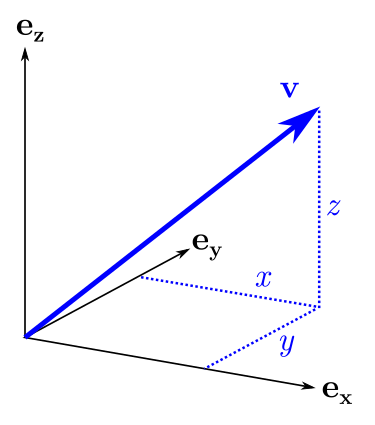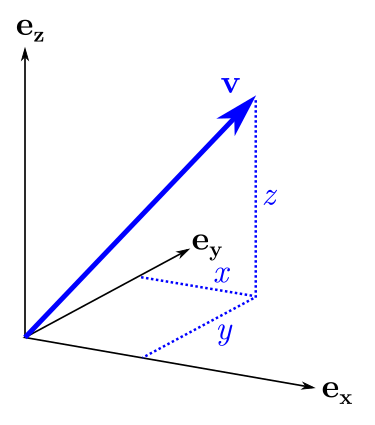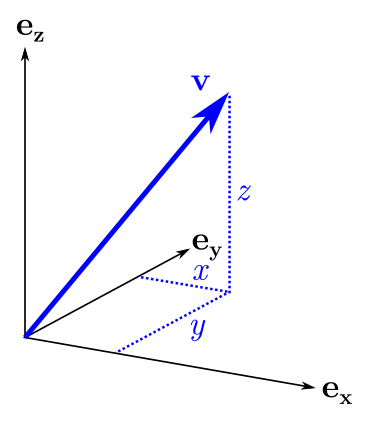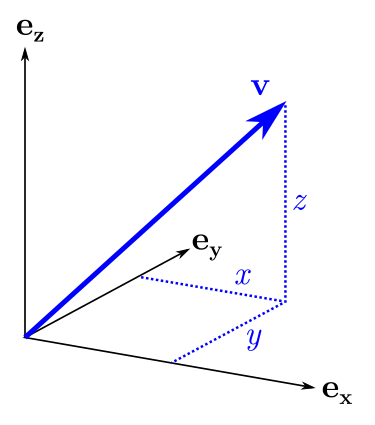
, . $$$v=(x, y, z)$, , $$$v$ :

$$

$$v=x{\bf e_x}+y{\bf e_y}+z{\bf e_z}$$

$$${\bf e_x}$, $$${\bf e_y}$, $$${\bf e_z}$ $$, $$$y$, $$$z$. $$$B$ :

$$

$$B=p{\bf e_{yz}}+q{\bf e_{zx}}+r{\bf e_{xy}}$$

$$${\bf e_{xy}}$ — , $$$xy$. $$${\bf e_{yz}}$ $$${\bf e_{zx}}$ . , , . " " $$$(p, q, r)$, .



:

$$

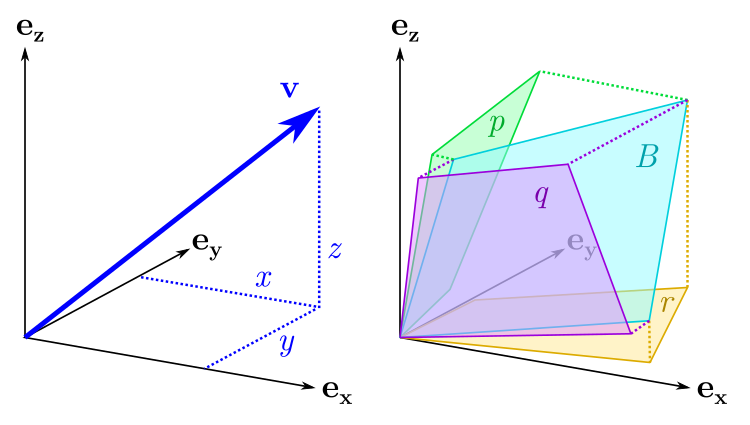
$$T=t{\bf e_{xyz}}$$

, 3D , : "" $$$(xyz)$. — $$${\bf e_{xyz}}$ .

, : ( 1), ( 2) ( 3). 0. , , , $$$\wedge$. , , :

$$

$${\bf e_x}\wedge{\bf e_y} = {\bf e_{xy}}$$

, , . , ( ).

, "" . , , . , .

, , .

$$

$${\bf e_x}\wedge{\bf e_y}\wedge{\bf e_z} = {\bf e_{xy}}\wedge{\bf e_z}={\bf e_{xyz}}$$

" ", , , .

, . . $$$a$ :

$$

$$(au)\wedge v=u\wedge (av) = a(u\wedge v)$$

, . $$$u, v$ :

$$

$$u\wedge v=-(v\wedge u)$$

. -, : $$$v\wedge v=0$. , . , $$$u\wedge v=0$ $$$u$ $$$v$ . , $$$u\wedge v\wedge w=0$ $$$u, v, w$ .

3 . , .

$$$k$-

, , — , — . ?

, , - . $$$a>0$ , $$$a, a^2, a^3$ . , , .

, :

$$

$$v\mapsto Mv$$

$$

$$\begin{bmatrix} x \\ y \\ z \end{bmatrix} \mapsto \begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} ax \\ ay \\. az \end{bmatrix} = av$$

$$$v$ , $$$x, y, z$, , $$$a$ , , .

? ( ), . . , , :

$$

$$\begin{aligned} B &= u \wedge v \\ (u \wedge v) &\mapsto (Mu) \wedge (Mv) \\ &= (au) \wedge (av) \\ &= a^2 (u \wedge v) \\ &= a^2 B \end{aligned}$$

! , $$$a$, $$$a^2$, .

, . , - $$$a^3$. :

$$

$$\begin{aligned} T &= (u \wedge v \wedge w) \\ (u \wedge v \wedge w) &\mapsto (Mu) \wedge (Mv) \wedge (Mw) \\ &= (au) \wedge (av) \wedge (aw) \\ &= a^3 (u \wedge v \wedge w) \\ &= a^3 T \end{aligned}$$

. , ?

, . 3 $$$x$, . :

$$

$$M = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

: $$$x$ 3, $$$y, z$ . , : , $$$x$ , $$$yz$ — .



? . , "" . $$$x$ , . : , $$$yz$, , , $$$x$, .



, . , , :

$$

$$B = p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}$$

$$$M$ , . $$$M$ :

$$

$$\begin{aligned} {\bf e_{yz}} = {\bf e_y} \wedge {\bf e_z} \quad &\mapsto \quad (M{\bf e_y}) \wedge (M{\bf e_z}) = {\bf e_y} \wedge {\bf e_z} = {\bf e_{yz}} \\ {\bf e_{zx}} = {\bf e_z} \wedge {\bf e_x} \quad &\mapsto \quad (M{\bf e_z}) \wedge (M{\bf e_x}) = {\bf e_z} \wedge 3{\bf e_x} = 3{\bf e_{zx}} \\ {\bf e_{xy}} = {\bf e_x} \wedge {\bf e_y} \quad &\mapsto \quad (M{\bf e_x}) \wedge (M{\bf e_y}) = 3{\bf e_x} \wedge {\bf e_y} = 3{\bf e_{xy}} \end{aligned}$$

: $$$\bf e_{yz}$ , $$$\bf e_{zx}$ $$$\bf e_{xy}$ 3, $$$x$.

, $$$M$ $$$B$:

$$

$$B \mapsto p \, {\bf e_{yz}} + 3q \, {\bf e_{zx}} + 3r \, {\bf e_{xy}}$$

, , $$$B$ , :

$$

$$\begin{bmatrix} p \\ q \\ r \end{bmatrix} \mapsto \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} p \\ q \\ r \end{bmatrix} = \begin{bmatrix} p \\ 3q \\ 3r \end{bmatrix}$$

, , . : $$$M$ .

: $$$M$ :

$$

$$M^{-T} = \begin{bmatrix} \tfrac{1}{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

?

, — $$$M$.

$$$\det M$. ( $$$M$ , $$$\det M$). $$$M$ . , , !

— , . .

$$$n\times n$ . $$$i$- $$$j$- :

1. $$$n\times n$ $$$i$ $$$j$. $$$(n-1)\times (n-1)$.
2. .
3. $$$(-1)^{i+j}$, $$$i+j$ . !

$$$n\times n$, .

, ? $$$p \, {\bf e_{yz}}$. $$$yz$, , $$$M$ $$$y$ $$$z$. $$$1,1$ $$$M$ $$$2\times2$, $$$M$ $$$y$ $$$z$. , , $$$yz$!

- , $$${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ , , $$$M$ . , , $$$M$ . , , .

( , . $$${\bf e_{xz}}$ $$${\bf e_{zx}}$. .)

, , $$$n$ $$$(n-1)$- . , $$$k$- $$$(n-k)$- , $$$n-k$ .

. . : 3D. , $$$(p, q, r)$ — $$$(x, y, z)$ !

. , . , $$$B$ :

$$

$$B\wedge v=0$$

$$$v$, $$$B$ , . , , , $$$B$ $$$v$ .

:

$$

$$\begin{gathered} (p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}) \wedge (x \, {\bf e_x} + y \, {\bf e_y} + z \, {\bf e_z}) = 0 \\ (px \, {\bf e_{yzx}} + qy \, {\bf e_{zxy}} + rz \, {\bf e_{xyz}}) = 0 \\ (px + qy + rz) {\bf e_{xyz}} = 0 \\ px + qy + rz = 0 \\ \end{gathered}$$

. , , (, $$${\bf e_{yz}} \wedge {\bf e_y} = 0$). $$$\bf e_{xyz}$, , . . , $$$\bf e_{xyz}$ .

$$$(p, q, r)$ $$$(x, y, z)$! , $$$n\cdot v = 0$ $$$n=(p, q, r)$.

, $$$(p, q, r)$ $$${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ $$${\bf e_x}, {\bf e_y}, {\bf e_z}$. , . , . .

, - . — . ( ) " ".

, . , "" , . ? , , ? , , ( ). .

: , , -3 3. , $$$k$- $$$k$0 à 3. Mais qu'en est-il des unités vectorielles avec des degrés d'échelle négatifs? Existent-ils? Si c'est vrai, que sont-ils?

Dans le prochain épisode, nous creuserons encore plus profondément et compliquerons encore plus notre histoire géométrique.